Integración doble en coordenadas polares

Cálculo en Varias Variables - Escuela de Matemáticas
Universidad Nacional, sede Medellín
Clase 13. Integrales dobles en coordenadas polares
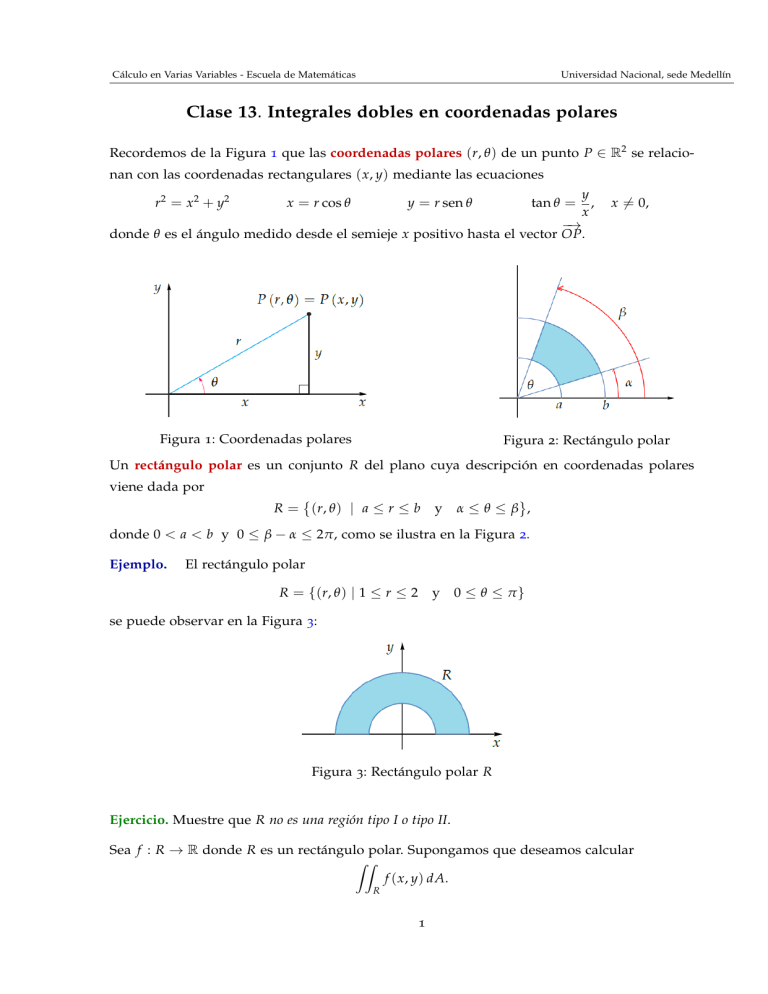
Recordemos de la Figura 1 que las coordenadas polares (r, θ ) de un punto P ∈ R2 se relacionan con las coordenadas rectangulares ( x, y) mediante las ecuaciones
r 2 = x 2 + y2
x = r cos θ
y = r sen θ
tan θ =
y
,
x
x 6= 0,
−→
donde θ es el ángulo medido desde el semieje x positivo hasta el vector OP.
Figura 1: Coordenadas polares
Figura 2: Rectángulo polar
Un rectángulo polar es un conjunto R del plano cuya descripción en coordenadas polares
viene dada por
R = (r, θ ) | a ≤ r ≤ b
y
α≤θ≤β ,
donde 0 < a < b y 0 ≤ β − α ≤ 2π, como se ilustra en la Figura 2.
Ejemplo.
El rectángulo polar
R = {(r, θ ) | 1 ≤ r ≤ 2
y
0 ≤ θ ≤ π}
se puede observar en la Figura 3:
Figura 3: Rectángulo polar R
Ejercicio. Muestre que R no es una región tipo I o tipo II.
Sea f : R → R donde R es un rectángulo polar. Supongamos que deseamos calcular
ZZ
f ( x, y) dA.
R
1
Cálculo en Varias Variables - Escuela de Matemáticas
Universidad Nacional, sede Medellín
Aunque su descripción en coordenadas cartesianas puede ser complicada, R se describe fácilmente en coordenadas polares. Ahora veamos cómo usarlas para calcular la integral.
Primero, notemos que
R = (r, θ ) | a ≤ r ≤ b
y
α ≤ θ ≤ β = [ a, b] × [α, β]
b−a
y el intervalo [α, β] en
Dividamos el intervalo [ a, b] en m subintervalos de tamaño ∆r =
m
β−α
n subintervalos de tamaño ∆θ =
. De esta manera, el rectángulo polar queda divido en
n
los subrectángulos polares
Rij = (r, θ ) | ri−1 ≤ r ≤ ri ,
θ j −1 ≤ θ ≤ θ j ,
donde ri = a + i∆r,
θl = α + j∆θ,
como se muestra en la Figura 4.
Figura 4: Subdivisión de un rectángulo polar
Podemos calcular el área de Rij usando el hecho que el área de un sector de un círculo con
radio r y ángulo θ es 21 r2 θ. Así, al restar las áreas de dos sectores de esta clase (cada uno de
los cuales tiene ángulo central ∆θ = θ j − θ j−1 ), se encuentra que el área de Rij es
∆Ai
=
1 2
1
ri ∆θ − ri2−1 ∆θ
2
2
=
1 2
(r − ri2−1 ) ∆θ
2 i
=
1
(ri + ri−1 )(ri − ri−1 )∆θ
2
=
ri∗ ∆r ∆θ.
Ahora, una suma de Riemann representativa para la integral doble es
n X
m
X
f (ri∗ cos(θ j∗ ), ri∗ sen(θ j∗ )) Área Rij ,
i =1 j =1
de donde
ZZ
f ( x, y) dA =
lı́m
m,n→∞
R
=
lı́m
m,n→∞
n X
m
X
f (ri∗ cos(θ j∗ ), ri∗ sen(θ j∗ )) Área Rij
i =1 j =1
n X
m
X
i =1 j =1
2
f (ri∗ cos(θ j∗ ), ri∗ sen(θ j∗ )) ri∗ ∆r∆θ.
Cálculo en Varias Variables - Escuela de Matemáticas
Universidad Nacional, sede Medellín
Teniendo en cuenta la definición de la integral doble en términos de sumas de Riemann, vemos
que el cambio de coordenadas cartesianas a coordenadas polares en una integral doble nos
permite concluir que
ZZ
β
Z
b
Z
f ( r cos θ, r sen θ ) r dr dθ.
f ( x, y) dA =
a
α
R
Nota: Preste especial atención al factor r adicional que aparece en la expresión en coordenadas
polares. Tenga cuidado de no olvidarlo.
Ejemplos.
ZZ
(3x + 4y2 ) dA, donde R es la región del semiplano superior
1. Evaluemos la integral
R
limitada por x2 + y2 = 1 y x2 + y2 = 4, como se muestra en la Figura 5.
Figura 5: Región polar
La región R puede ser descrita en coordenadas cartesianas como
R = ( x, y) | 1 ≤ x2 + y2 ≤ 4
y≥0 ,
y
pero luce más sencilla al expresarla en coordenadas polares
R = (r, θ ) | 1 ≤ r ≤ 2
y
0≤θ≤π .
Así que al hacer x = r cos θ, y = r sen θ, tenemos que
Z
V (S)
π
Z
2
=
0
Z
3r cos θ + 4r2 sen2 θ r dr dθ
1
π
Z
=
2
2
3
2
3r cos θ + 4r sen θ dr dθ
0
Z
=
Z
=
1
π
π
=
0
3
4
2
r cos θ + r sen θ
0
7 cos θ + 15 sen2 θ dθ
2
3
15π
.
2
dθ
1
Cálculo en Varias Variables - Escuela de Matemáticas
Universidad Nacional, sede Medellín
2. Encontremos el volumen del sólido S acotado por el paraboloide z = 10 − 3x2 − 3y2 y el
plano z = 4, como se observa en la Figura 6.
Figura 6: Sólido acotado por el paraboloide z = 10 − 3x2 − 3y2 y el plano z = 4
La región de integración se obtiene al proyectar la intersección del paraboloide con el
plano z = 4 en el plano xy. Es decir, 4 = 10 − 3x2 − 3y2 , de donde x2 + y2 = 2 :
Figura 7: x2 + y2 = 2
Por tanto, la región de integración es
R = {( x, y) | x2 + y2 ≤ 2} = {(r, θ ) | 0 ≤ r ≤
√
2
y
0 ≤ θ ≤ 2π }.
De donde,
ZZ
V (S)
=
(10 − 3x2 − 3y2 − 4) dA
ZZ
R
R
Z
=
6 − 3( x2 + y2 ) dA
=
2π
√
Z
3
0
2
√
2
(2 − r ) r dr dθ
0
Z
=
6π
0
4
2
(2r − r3 ) dr
= 6π.
Cálculo en Varias Variables - Escuela de Matemáticas
Universidad Nacional, sede Medellín
3. Calculemos el volumen del sólido S que se encuentra por encima del cono z =
p
x 2 + y2
y por debajo de la esfera x2 + y2 + z2 = 1, como se muestra en la Figura 8.
Figura 8: Sólido S y región de integración
La región de integración se encuentra en la intersección del cono y la esfera. Ésta es:
q
zcono = zesfera
q
2
2
x +y =
1 − x 2 − y2
x 2 + y2 = 1 − x 2 − y2
1
x 2 + y2 =
.
2
Por tanto la región de integración es
R = ( x, y) | x2 + y2 ≤
1
2
,
que puede ser descrita más fácilmente en coordenadas polares, como
n
o
√
R = (r, θ ) | 0 ≤ r ≤ 22 y 0 ≤ θ ≤ 2π .
Así, el volumen del sólido S es:
ZZ
ZZ
V (S) =
(zesfera − zcono ) dA =
R
q
q
1 − x2 − y2 − x2 + y2 dA.
R
De donde,
√
ZZ
V (S)
=
p
1 − r2
Z
− r r dr dθ
2π
=
0
R
√
Z
=
2π
Z
dθ
0
2
2
Z
p
r 1 − r2 − r2 dr
0
5
=
2π
3
2
2
p
1 − r2 − r r dr dθ
0
√ !
2
1−
.
2
Cálculo en Varias Variables - Escuela de Matemáticas
Universidad Nacional, sede Medellín
Podemos considerar regiones más generales como la que se ilustra en la Figura 9:
Figura 9: Región polar
Si f es continua en una región polar de la forma
D = {(r, θ ) | α ≤ θ ≤ β
entonces
ZZ
β
Z
Z
Ejemplo.
h1 (θ ) ≤ r ≤ h2 (θ )} ,
h2 ( θ )
f ( x, y) dA =
f ( r cos θ, r sen θ ) r dr dθ.
α
D
y
h1 ( θ )
Encuentre el volumen del sólido S que está debajo del paraboloide z = x2 + y2 ,
encima del plano xy y dentro del cilindro x2 + y2 = 2x.
x2 + y2 = 2x
( x − 1)2 + y2 = 1
Figura 10: Sólido S
Figura 11: Región D
Observe que D = {(r, θ ) | −π/2 ≤ θ ≤ π/2 y 0 ≤ r ≤ 2 cos θ } . Por consiguiente,
ZZ
Z π/2 Z 2 cos θ
3π
V (S) =
x2 + y2 dA =
r2 r dr dθ =
.
2
−π/2 0
D
6