PROBLEMARIO MATEMÁTICAS IV 3 parcial

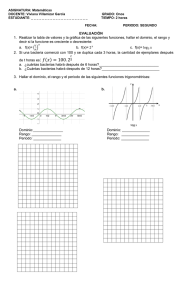
PROBLEMARIO MATEMÁTICAS IV
PARCIAL III
Identifica y determina los valores de las asíntotas vertical, horizontal u oblicua según
presenten las funciones dadas. Traza las graficas correspondientes para cada una de las
asíntotas
I.
f ( x) =
x+4
x 2 - 16
f ( x) =
3x
3x - 27 x
2
x2 - 4
f ( x) =
x +1
f ( x) =
x +1
2x2 - x - 1
f ( x) =
x -5
x - 8 x - 12
2
II. Resuelve los siguientes problemas exponenciales.
1) Se ha detectado que cierto tipo de insecto que amenaza los sembrados de maíz
tiene una razón de crecimiento de e0.03t por hora. Si al inicio hay 50 de estos
ejemplares, a) ¿Cuántos habrá en un día completo? b) ¿Cuántos habrá en una
semana?
2) Si se conoce que la cantidad de crecimiento de cierto elemento químico es de
12ml, y este se degenera a una razón de -0.0578 por día, a) ¿Cuánto material habrá
dentro de un mes? b) ¿Cuánto material habrá en un año?
3) Un laboratorio químico determina que para ciertos cultivos el numero de bacterias
está dado por la expresión N(t)= Be0.09t, donde t expresa horas. Determina:
a) ¿Cuál será el valor de B, considerando que inicialmente existen 250 bacterias?
b) ¿Cuántas bacterias habrá en un día?
c) ¿Cuántas bacterias habrá en 4 y medio?
d) ¿Cuántas baterías habrá en una semana?
e) ¿La grafica de la función corresponde al crecimiento o decrecimiento exponencial?
III. Transforma las siguientes expresiones en logarítmicas o exponenciales según sea el
caso y encuentra sus respectivos resultados.
a) 82
b) log100,000,000
c) log5 390,628
25
d)
e)
f)
g)
h)
ln 1
ln 28.693
ln .0034
i)
j)
k)
l)
m)
n)
o)
p)
q)
r)
54
log36 6
ln12
log254
log100,000,000,000,000
36
e23
94
Log399
Log71049
log3 27
IV. Desarrolla las siguientes expresiones aplicando las propiedades de los logaritmos.
a) log x
b) logx3
xy
c) log
z
d) log x3 y 2
x5 y
3
z
f) log7 + log4 - log2
e) log2
x2 y3
g) log
z