no El estadígrafo de prueba, para valores de

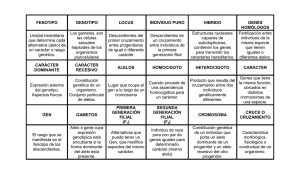
140
El estadígrafo de prueba, para valores de n suficientemente grande y valores de o3 € %,
es D œ !
#
5
3œ"
Ð o3 e3 Ñ#
e3
, cuya distribución es aproximadamente ji cuadrada con ( k - 1 ) grados de
libertad, cuya notación es ;# Ð5  "Ñ.
4° La región crítica es del tipo unilateral derecha , lo que es usual para pruebas basadas en la
distribución ji cuadrada, pues se rechazará si las diferencias entre lo observado y lo esperado
son grandes, luego RC œ Ö D# ÎD#  ;#"! Ð5  "Ñ ×.
Ejemplos 6.1
a) Se asegura que una mezcla de semillas para césped contiene tres variedades de pasto,
lolium perenne, lawn grass y festuca rubra en proporciones de 20% , 50% y 30%
respectivamente. Se desea corroborar tal información para lo cual se hace el siguiente
planteamiento:
1) H! À T" œ !ß #! , T2 œ !ß &! , T$ œ !ß $! versus H" : b T3 Á T3! , donde la clase 1 es lolium,
la clase 2 es lawn grass y la 3 corresponde a festuca.
#) Se usará != 0,05
3) el estadígrafo de prueba a utilizar es D œ !
#
3
3œ"
Ð o3 e3 Ñ#
e3
¸ ;# Ð#Ñ.
4) La región crítica es RC œ Ö D# ÎD#  ;#!ß*& Ð#Ñ œ &ß **"×.
5) Con el objeto de corroborar o rechazar la hipótesis nula se ponen a germinar 300 semillas
de la mezcla. Días después se identifica la especie de cada brote y se cuenta por especie,
obteniéndose la siguiente distribución: 70 brotes de lolium, 120 de lawn grass y 110 de festuca,
que corresponden a las frecuencias observadas (o3 Ñ. Se deben calcular las respectivas
frecuencias esperadas e3 œ $!!‡T3 , todo lo cual se resume en la siguiente tabla, a partir de la
que se obtiene D# :
Ð(!  '!Ñ#
Ð"#!  "&! Ñ#
Ð""!  *! Ñ#
var l.p l.g
f.r
Total
Ê D# œ
+
+
œ "#ß " − RC
'!
"&!
*!
o3
e3
70
60
120
150
110
90
300
300
Ê rechazar H! .
6) Los datos obtenidos en la muestra de 300 semillas establecen que es muy improbable que
sea verdadera la afirmación de que la proporción de las especies sea la especificada en la
hipótesis nula, al nivel del 5%.
b) En genética en un cruce dihíbrido entre dos plantas heterocigóticas de guisantes, cada
una con el genotipo RrAa y genes independientes, pueden producir uno de los tipos de
gametos RA ó Ra ó rA ó ra , donde R representa el alelo dominante de la forma
redondeada, r el alelo recesivo rugoso, A el alelo dominante de color amarillo y a el alelo
recesivo de color verde. Según la Ley de Mendel, la segregación de caracteres independientes,
RA , Ra , rA y ra se dan en la proporción 9:3:3:1. Para corroborar la ley anterior se analizaron
480 casos encontrándose la siguiente segregación fenotípica: 282 del tipo RA , 80 del tipo Ra
, 95 del tipo rA y 23 del tipo ra. ¿ Los datos muestrales obtenidos entregan evidencia
suficiente para contradecir la Ley de Mendel ?