Mathcad - Resistencia1_ej3 - Universidad del Valle de Guatemala

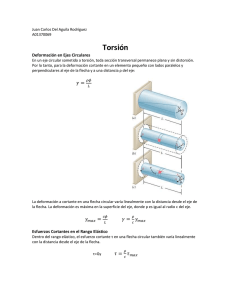
Universidad del Valle de Guatemala
Resistencia de Materiales 1
Ejemplo 3
Torsión
TORSIÓN
TRANSMISIÓN DE POTENCIA POR MEDIO DE EJES CIRCULARES
Un motor que impulsa un eje sólido circular de acero transmite 40hp a un
engrane en B. El esfuerzo cortante permisible en el acero es de 6000lb/pulg2 .
a) ¿Cuál es el diámetro d requerido para el eje si éste es operado a 500rpm?
b) ¿Cuál es el diámetro d requerido si se opera a 3000rpm?
SOLUCIÓN
a) Motor operando a 500rpm.
Conocida la potencia y la velocidad de rotación, podemos encontrar el par
T que actúa sobre el eje usando la ecuación:
H=
2  π n  T
60 ( 550 )
=
2  π n  T
(donde n=rpm, T=lb/pie, H=hp)
33000
Despejamos T en esa ecuación y obtenemos
Resultado =
n  500
H  40
H=
2  π n  T
60 ( 550 )
solve T 
1320
π
Resistencia de Materiales 1
Ejemplo 3
Torsión
El eje transmite este par del motor al engranaje
El esfuerzo cortante máximo en el eje puede obtenerse con la fórmula
modificada de la torsión
τmax =
16 T
π d
3
Despejamos en esta ecuación el diámetro d, sustituimos τperm por
τmax y obtenemos
1


3


45378


1


3


15 π
 1

1


 3 3  15126 3   1  3 i 
Resultado = T  5042
solve d  

1


τperm  6000
3


30 π
16 T


τperm =
1
1


3
π d
 3 3  15126 3   1  3 i 


1


3


30 π
Tomamos la solución real y obtenemos como valor del diámetro mínimo
para no exceder el esfuerzo cortante permisible.
3
d 
45378
3375 π
 1.624
b ) Motor operando a 3000rpm.
Siguiendo el mismo procedimiento del inciso a) y obtenemos
Resultado =
n  3000
H  40
H=
2  π n  T
60 ( 550 )
solve T 
220
π
Resistencia de Materiales 1
Ejemplo 3
Torsión
3
d 
16 840.3
π 6000
 0.893
Este ejemplo muestra que entre mayor sea la velocidad de rotación,
menor es el tamaño requerido para el eje (para la misma potencia y
el mismo esfuerzo permisible)
fuente: mecanica de materiales, james m. gere, sexta edición
capítulo 3 Ejemplo 3-7