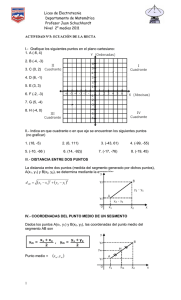
Calcular de forma aproximada, mediante simulación:
Anuncio

PRÁCTICAS DE SIMULACIÓN Calcular de forma aproximada, mediante simulación: 1. En un segmento AB de longitud 1 se señala aleatoriamente un punto P a distancia x del extremo A. Después se señala otro punto Q a distancia y del punto P. ¿Cuál es la probabilidad de que se pueda formar un triángulo con los segmentos AP, PQ y QB? 2. En un segmento AB de longitud 1 se señalan dos puntos P y Q a distancia x e y del extremo A, respectivamente. ¿Cuál es la probabilidad de que se pueda formar un triángulo con los segmentos AP, PQ y QB? 3. En un lanzamiento de tres dados, ¿cuál es la probabilidad de obtener suma igual a 12? 4. Las valoraciones obtenidas en una prueba tienen una distribución normal de media 5,8 y desviación típica 1,75. Si sólo pasan la prueba aquellas personas que sobrepasan 6,5 puntos ¿qué porcentaje de aprobados es de esperar? 5. Calcular de forma aproximada la distribución de probabilidad de la suma de puntos obtenidos al lanzar dos dados. 6. Encontrar el máximo y el mínimo de la función y=x3-7x2+14x-8 en el intervalo (1,4) 7. I = ∫01 1 - x 2 dx = π 4 π 2 πx 11 8. I = ∫0 1 + sen dx = 3 2 3 2