Dado un experimento aleatorio, una variable aleatoria X es una

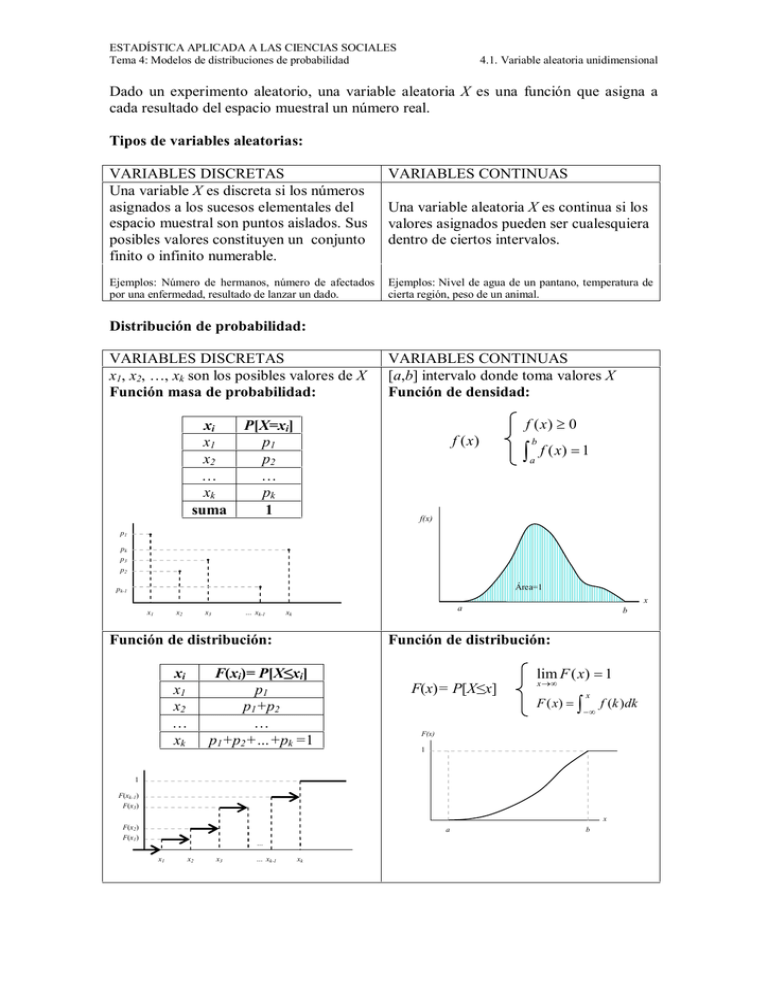
ESTADÍSTICA APLICADA A LAS CIENCIAS SOCIALES
Tema 4: Modelos de distribuciones de probabilidad
4.1. Variable aleatoria unidimensional
Dado un experimento aleatorio, una variable aleatoria X es una función que asigna a
cada resultado del espacio muestral un número real.
Tipos de variables aleatorias:
VARIABLES DISCRETAS
Una variable X es discreta si los números
asignados a los sucesos elementales del
espacio muestral son puntos aislados. Sus
posibles valores constituyen un conjunto
finito o infinito numerable.
Ejemplos: Número de hermanos, número de afectados
por una enfermedad, resultado de lanzar un dado.
VARIABLES CONTINUAS
Una variable aleatoria X es continua si los
valores asignados pueden ser cualesquiera
dentro de ciertos intervalos.
Ejemplos: Nivel de agua de un pantano, temperatura de
cierta región, peso de un animal.
Distribución de probabilidad:
VARIABLES DISCRETAS
x1, x2, …, xk son los posibles valores de X
Función masa de probabilidad:
xi
x1
x2
…
xk
suma
P[X=xi]
p1
p2
…
pk
1
VARIABLES CONTINUAS
[a,b] intervalo donde toma valores X
Función de densidad:
f (x )
f ( x)  0
 a f ( x)  1
b
f(x)
p1
pk
p3
p2
Área=1
pk-1
x1
x2
x3
… xk-1
a
xk
Función de distribución:
xi
x1
x2
…
xk
b
Función de distribución:
F(xi)= P[X≤xi]
p1
p1+p2
…
p1+p2+…+pk =1
F(x)= P[X≤x]
lim F ( x)  1
x 
F ( x)  
x

f (k ) dk
F(x)
1
1
F(xk-1)
F(x3)
F(x2)
F(x1)
a
…
x1
x2
x3
… xk-1
xk
b
x
x
ESTADÍSTICA APLICADA A LAS CIENCIAS SOCIALES
Tema 4: Modelos de distribuciones de probabilidad
4.2. Modelos de probabilidad
DISTRIBUCIÓN BINOMIAL
Se repite un experimento n veces de forma idéntica e independiente. Los resultados de
cada realización del experimento se clasifican en dos categorías: éxito y fracaso, que
son incompatibles.
Llamamos p a la probabilidad de que ocurra éxito en una realización.
Llamamos q a la probabilidad de que ocurra fracaso (q=1-p).
La variable definida como X: “número de éxitos en las n realizaciones del experimento”
tiene distribución binomial de parámetros n y p:
X  Bn, p 
 n k
n k
Función masa de probabilidad  P X  k     p 1  p 
k 
Esperanza  E X   np
Varianza  Var  X   npq
DISTRIBUCIÓN POISSON
Se observa la ocurrencia de determinados sucesos que llamamos éxitos en un intervalo
de tiempo, área, longitud o volumen de forma que:
1. El número medio de veces que ocurre el suceso éxito (ë) es constante en ese
tiempo, área, longitud o volumen.
2. El número de ocurrencias de dichos sucesos en dos intervalos o regiones
diferentes son independientes de forma que el número de ocurrencias en un
intervalo no afecta al número de sucesos en cualquier otro intervalo disjunto.
La variable X: “número de éxitos ocurridos en un intervalo dado” se modeliza según una
distribución de Poisson de parámetro ë.
X  P 
P X  k   e 
Función masa de probabilidad 
Esperanza  E X   
Varianza  Var  X   
k
k!
DISTRIBUCIÓN NORMAL
La variable continua X sigue una distribución normal de parámetros ì y ó si su función
de densidad es
f ( x) 
X  N  ;  
Esperanza 
Varianza 
Tipificación:
X  N ( , )  Z 
EX   
Var  X    2
X 
 N ( 0,1)

1
2
e

( x )2
2 2
ESTADÍSTICA APLICADA A LAS CIENCIAS SOCIALES
Tema 4: Modelos de distribuciones de probabilidad
4.3. Relación entre los modelos
APROXIMACIONES
N(np,
npq )
NORMAL
0.1< p<0.9
y
n≥30
)
ë≥10
B(n,p)
P(ë)
BINOMIAL
B(n,p)
N(ë,
POISSON
n≥30 y p<0.1
o
np≤5
P(ë=np)
Corrección por continuidad:
Cuando se aproxima un modelo Binomial o Poisson mediante un modelo normal, el
cambio de variable discreta a variable continua supone el problema de que para las
variables continuas P[X=k]=0. Para evitar este problema a la hora de calcular
probabilidades se realiza una corrección, llamada “corrección por continuidad”, de la
siguiente forma:
Determinar la probabilidad P[X=k] en una Binomial o Poisson será equivalente a
determinar la probabilidad en el intervalo (k-0.5, k+0.5) en un modelo normal.