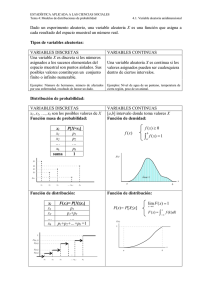
DISTRIBUCIÓN DE POISSON

DISTRIBUCIÓN DE POISSON
POISSON
Siméon Denis Poisson, (1781-1840), astronauta
francés, alumno de Laplace y Lagrange, en
Recherchés sur la probabilité des jugements...., un
trabajo importante en probabilidad publicado en el
año 1837, la distribución de Poisson recién
aparecía.
La distribución de Poisson describe la probabilidad como un acontecimiento
fortuito ocurrido en un tiempo o intervalo de espacio bajo las condiciones que la
probabilidad de un acontecimiento ocurre es muy pequeña, pero el número de
intentos es muy grande, entonces el evento actual ocurre algunas veces.
Poisson, usos
“La probabilidad de obtener “X “ éxitos en un intervalo continuo”
Se emplea para describir varios procesos:
Distribución de las llamadas telefónicas que llagan a un conmutador
La demanda de servicios en un hospital por parte de los pacientes
Los arribos de los camiones y automóviles a la caseta de cobro
El número de accidentes en un cruce
El número de defectos en una tela por m2
El número de bacterias por cm2
Poisson, características
Características
El número medio (promedio) de eventos en el espacio temporal o región específica de
interés, por lo general esta media se representa por la lambda griega (λ
λ)
El número de resultados que ocurren en un intervalo de tiempo o región específicos
es independiente de el número que ocurre en cualquier otro intervalo de tiempo o
región
La probabilidad de que un resultado muy pequeño ocurra en un intervalo de tiempo
muy corto o en una región pequeña es proporcional a la longitud del intervalo de
tiempo o al tamaño de la región
La probabilidad de que más de un resultado ocurra en un intervalo de tiempo tan
corto o en esa región tan pequeña es inapreciable, que se puede asignar el valor de
0
Fórmula de Poisson
P(x I λ) = λx * e-λλ
x!
P (x I λ) = la probabilidad de que ocurran X éxitos cuando el número promedio de ocurrencia de ellos
es λ
λ media o promedio de éxitos por unidad de tiempo, área o producto
e es la constante 2.7183, base de los logaritmos naturales, en tanto que los valores de e-λλ pueden
obtenerse de tablas.
X señala un valor específico que la variable pueda tomar (el número de éxitos que deseamos ocurran)
Por definición, el valor esperado (media en el intervalo o región de interés) de una distribución de
probabilidad de Poisson es igual a la media de la distribución.
E(X) = λ
La varianza del número de eventos de una distribución de probabilidad de Poisson también es igual a la
media de la distribución λ. De este modo, la desviación estándar es la raíz cuadrada de λ.
V(X) = λ
σ = √λ
Ejemplos
P(x I λ) = λx * e-λλ
x!
Supóngase que estamos investigando la seguridad de un crucero muy peligroso. Los archivos de la policía
indican una media de cinco accidentes por mes en él. El número de accidentes está distribuido conforme a la
distribución de Poisson, y la división de seguridad en carreteras quiere calcular la probabilidad de
exactamente 0,1,2,3 y 4 accidentes en un mes determinado.
Aplicando la fórmula anterior:
P(0) = (5)0 (e-5) /0! = 0.00674
P(1) = (5)1 (e-5) /1! = 0.03370
P(2) = (5)2 (e-5) /2! = 0.08425
P(3) = (5)3 (e-5) /3! = 0.14042
P(4) = (5)4 (e-5) /4! = 0.17552
Para saber cual es la probabilidad en 3 o menos (X ≤ 3), sumaremos las probabilidades de 0,1,2,3 lo que
será igual a :
P(X ≤ 3) = P(0)+P(1)+P(2)+P(3) = 0.26511
Dado que la probabilidad de que haya 3 o menos accidentes es de 0.26511 entonces la probabilidad de que
ocurran más de tres (X > 3) debe ser = 1 –0.26511 = 0.73489.
En una tienda de telas, un promedio de 12 personas por hora le hacen preguntas a un decorador. La
probabilidad de que 3 ó más personas se acerquen al decorador para hacerle preguntas en un periodo de 10
minutos.
Promedio por hora =12
λ = promedio por 10 minutos = 12/6 = 2.0
P (X ≥ 3 I λ = 2) = P (X=3 I λ = 2) + P (X=4 I λ = 2) + P (X=5 I λ = 2) + …
Ó
P (X ≤ 2 I λ = 2) = 1 – [ P (X=0 I λ = 2) + P (X=1 I λ = 2) + P (X=2 I λ = 2) ]
Solución 1
P (X=3 I λ = 2) = 0.1804
P (X=4 I λ = 2) = 0.0902
P (X=5 I λ = 2) = 0.0361
P (X=6 I λ = 2) = 0.0120
P (X=7 I λ = 2) = 0.0034
P (X=8 I λ = 2) = 0.0009
P (X=9 I λ = 2) = 0.0002
P (X ≥ 3 I λ = 2) = 0.3232
Solución 2
P (X= 0 I λ = 2) = 0.1353
P (X= 1 I λ = 2) = 0.2707
P (X= 2 I λ = 2) = 0.2707
P (X ≥ 3 I λ = 2) = 0.3232
Aproximación de la distribución
binomial por una de Poisson
Algunas veces, si se desea evitar el tedioso trabajo de calcular las distribuciones binomiales, sobre todo
si n (ensayos) es muy grande y p o q (éxito y fracaso) es muy pequeña, se puede usar a cambio la de
Poisson, pero debe cumplir con ciertas condiciones como :
n ≥ 30
np ó nq < 5
En los casos en que se satisfacen tales condiciones, podemos sustituir la media de la distribución
binomial en lugar de la media de la distribución de Poisson de modo:
λ=np
Ejemplo: Se sabe que 1% de los artículos de un gran embarque de transistores procedente de un proveedor
son defectuosos. Si se selecciona aleatoriamente una muestra de 30 transistores, la probabilidad de que
dos o más de ellos sean defectuosos.
P (X ≥ 2 I n=30, p= 0.01) = P (X=2) + P (X=3) + …= 0.0328+0.0031+0.0002 = 0.0361
Si λ=np=30(0.01) = 0.3, la aproximación de Poisson del anterior valor de probabilidad es
P (X ≥ 2 I λ = 0.3) = P (X=2) + P (X=3) + …= 0.0333 + 0.0033 + 0.0002 = 0.0368
Así la diferencia entre la aproximación de Poisson y el valor de probabilidad binomial real es de sólo 0.0007