Operaciones Internas y Estructuras Algebraicas

i
UNIVERSIDAD NACIONAL DE EDUCACIÓN
Enrique Guzmán y Valle
Alma Máter del Magisterio Nacional
FACULTAD DE CIENCIAS
Escuela Profesional de Matemática e Informática
OPERACIONES INTERNAS Y ESTRUCTURA ALGEBRAICA
Operaciones internas o ley de composición interna: Operaciones
asociativas y conmutativas, elemento neutro y elementos inversibles o
simetrizables Propiedades básicas. Las estructuras algebraicas y las
estructuras de la inteligencia. Didáctica de la estructura algebraica.
Examen de Suficiencia Profesional Res. N°1507-2019-D-FAC
Presentada por:
Mario Andres Auqui Caceres
Para optar al Título Profesional de Licenciado en Educación
Especialidad: Matemática e Informática
Lima, Perú
2019
ii
OPERACIONES INTERNAS Y ESTRUCTURA ALGEBRAICA
Operaciones internas o ley de composición interna: Operaciones
asociativas y conmutativas, elemento neutro y elementos inversibles o
simetrizables Propiedades básicas. Las estructuras algebraicas y las
estructuras de la inteligencia. Didáctica de la estructura algebraica.
Designación de Jurados Resolución N°1507-2019-D-FAC
______________________________
Dr. Narciso Fernández Saucedo
Presidente
______________________________
Mg. Julio Alejandro Mendoza García.
Secretario
______________________________
Dr. Leónidas Torres Anaya.
Vocal
Línea de investigación: Metodología y didáctica
UNIVERSIDAD NACIONAL DE EDUCACIÓN
Enrique Guzmán y Valle
Alma Máter del Magisterio Nacional
FACULTAD DE CIENCIAS
Dirección de la Unidad de Investigación
“Año del Bicentenario, de la consolidación de nuestra Independencia, y de la conmemoración de las
heroicas batallas de Junín y Ayacucho”
CONSTANCIA DE ORIGINALIDAD
N° 117 – 2024 – DUI – FAC – UNE
El Director de la Unidad de Investigación de la Facultad de Ciencias.
Hace constar que:
El Trabajo, titulado:
OPERACIONES INTERNAS Y ESTRUCTURA ALGEBRAICA Operaciones internas o ley de
composición interna: Operaciones asociativas y conmutativas, elemento neutro y
elementos inversibles o simetrizables Propiedades básicas. Las estructuras algebraicas y las
estructuras de la inteligencia. Didáctica de la estructura algebraica.
Del autor: Mario Andres Auqui Caceres ha sido sometida, en su versión final, al software Turnitin
y obtuvo un porcentaje del 18% de similitud con otras fuentes verificables, lo cual garantiza su
originalidad e integridad académica. Asimismo, se comprobó la aplicación de las normas APA de
acuerdo con las disposiciones vigentes.
Se expide la presente constancia p ara los fines pertinentes.
La Cantuta, 30 de mayo del 2024.
Mario Andres Auqui Caceres
Autor
DNI N° 09727202
iv
iii
Dedicatoria:
Este trabajo monográfico y su respectiva sustentación
se lo dedico a mis padres Mario y Victoria, y a mi hermano
Hugo, quienes en vida defendieron y lucharon por sus ideales
hasta el final de sus días.
iv
Índice de contenidos
Portada .................................................................................................................................... i
Hoja de firmas de jurados ......................................................................................................ii
Dedicatoria: ......................................................................................................................... iii
Indice de contenidos ............................................................................................................. iv
Lista de figuras ..................................................................................................................... vi
Introducción .........................................................................................................................vii
Capítulo I. Aspectos preliminares ..................................................................................... 9
1.1
Conjuntos ................................................................................................................... 9
1.2
Operaciones con conjuntos ...................................................................................... 10
1.3
Producto cartesiano .................................................................................................. 10
1.4
Relaciones binarias .................................................................................................. 10
1.5
Funciones ................................................................................................................. 11
Capítulo II: Leyes de composición interna .................................................................... 12
2.1
Breve referencia histórica ........................................................................................ 12
2.2
Ley de composición interna ..................................................................................... 13
2.3
Leyes asociativas ..................................................................................................... 17
2.4
Elementos permutables ............................................................................................ 20
2.5
Elemento central y centro de un conjunto ............................................................... 22
2.6
Leyes conmutativas ................................................................................................. 24
2.8
Leyes distributivas ................................................................................................... 26
2.9
Elementos distinguidos y regulares ......................................................................... 27
2.9.1 Elemento neutro ............................................................................................. 27
2.9.2 Elemento simétrico ........................................................................................ 28
v
2.9.3 Elemento absorbente...................................................................................... 30
2.9.4 Elementos regulares ....................................................................................... 32
Capítulo III. Estructuras algebraicas ............................................................................. 33
3.1
Estructura algebraica ............................................................................................... 33
3.2
Monoides ................................................................................................................. 33
3.3
Semigrupos .............................................................................................................. 34
3.4
Grupos...................................................................................................................... 35
3.5
Subgrupos ................................................................................................................ 40
3.6
Homomorfismo de grupos ....................................................................................... 42
3.7
Anillos...................................................................................................................... 45
3.7.1 Anillo conmutativo ........................................................................................ 46
3.7.2 Anillo con identidad ...................................................................................... 46
3.8
Cuerpos .................................................................................................................... 52
3.8.1 Propiedades de los cuerpos ............................................................................ 54
3.8.2 Demostración de algunas propiedades: ......................................................... 54
3.8.2.1 Propiedad del elemento absorbente: ............................................................ 55
3.9
Espacio vectorial ...................................................................................................... 56
3.10
Las estructuras algebraicas y las estructuras de la inteligencia ............................... 62
Aplicación didáctica ............................................................................................................ 65
Síntesis ................................................................................................................................. 72
Apreciación crítica y sugerencias ........................................................................................ 73
Referencias .......................................................................................................................... 75
vi
Lista de figuras
Figura 1. Síntesis ................................................................................................................ 63
Figura 2. Cuadro de estructuras algebraicas ....................................................................... 64
vii
Introducción
En el presente trabajo monográfico se desarrollan las Operaciones internas y las
estructuras algebraicas asignado por sorteo para rendir el examen de suficiencia y optar el
título de licenciado en educación en la especialidad de matemática e informática.
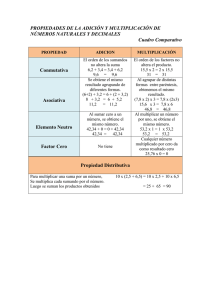
Desde los primeros grados de educación primaria estamos familiarizados con las
operaciones de adición, sustracción, multiplicación y división de números naturales; así
como con algunas de sus propiedades. Por ejemplo, el niño sabe que “el orden de los
factores no altera el producto” o que da lo mismo sumar “3+5” que “5+3”. El propósito
del presente trabajo es el estudio de operaciones como las que hemos mencionado y que de
acuerdo al conjunto donde están definidas tienen ciertas propiedades que le dan
determinada estructura.
En el primer capítulo se desarrollan de manera sucinta algunos conceptos previos
como los conjuntos, las relaciones binarias, las funciones y los sistemas numéricos, que
consideramos fundamentales para una comprensión de las operaciones internas y las
estructuras algebraicas.
En el segundo capítulo se desarrollan las operaciones internas llamadas también
leyes de composición interna, así como sus principales propiedades y algunos elementos
distinguidos. En el tercer capítulo se presentan las principales estructuras algebraicas,
como son los monoides, semigrupos, grupos, anillos, cuerpos y campos, haciendo especial
énfasis a través de los ejemplos en las estructuras algebraicas que poseen los diferentes
conjuntos numéricos con las operaciones usuales de adición y multiplicación.
Finalmente siguiendo el esquema propuesto de presentación de los trabajos
monográficos, se realiza una síntesis de la monografía, se propone la aplicación didáctica
del tema en mención en el nivel de educación de educación básica y en el nivel de
viii
educación superior, especialmente en la formación docente; y concluimos con una
apreciación crítica, y las respectivas conclusiones y sugerencias que se desprenden del
estudio realizado.
El autor.
9
Capítulo I.
Aspectos preliminares
1.1
Conjuntos
El término conjunto es un concepto primitivo o no definido; sin embargo, sabemos
que este concepto es sinónimo de agrupación, colección o conglomerado de objetos de
diversa naturaleza, concretos o abstractos. Por convenio los conjuntos se representan con
letras mayúsculas (A, B, C, …), mientras que a los objetos que lo conforman, llamados
elementos, se escriben entre llaves nombrándolos generalmente con letras minúsculas (a,
b, c, …, x, y, z). Gráficamente los conjuntos se representan usando el diagrama de Venn.
Ejemplos:
 Dado el conjunto de los números impares menores que 10, lo podemos representar
como A={1,3,5,7,9}; o gráficamente:
 Como vemos los elementos del conjunto A son 1, 3, 5, 7 y 9, lo que simbólicamente se
escribe 1∈A, 3∈A, …, y 9∈A.
10
 Pero, 11 no es elemento del conjunto A, por lo que escribimos 11∉A, que también se
lee “11 no pertenece al conjunto A”.
1.2
Operaciones con conjuntos
Dados los conjuntos A, B y el conjunto referencial U ; entonces definimos:
a. La reunión de conjuntos
b. Intersección de conjuntos
c. Diferencia de conjuntos
1.3
Producto cartesiano
a. Par ordenado. - Dados conjuntos A y B, y los elementos y, el par ordenado
se define
como:
Ejemplo:
2,3  2, 2,3
3,2  3, 3,2
Observación: 2,3  3,2
En general,
Nota:
 Definición: dado todo conjunto A y B, es llamado producto cartesiano AxB al conjunto:
1.4
Relaciones binarias
 Definición: dado ambos conjuntos no vacíos A y B (A≠∅ y B≠∅), una relación binaria
R de A en B, es cualquier subconjunto del producto cartesiano AxB; es decir:
11
a. Relaciones definidas sobre un conjunto: dado un conjunto A no vacío (A≠∅); una
“
relación binaria R definida sobre A es cualquier subconjunto del producto cartesiano
AxA.
Es decir: R⊂AxA
Ejemplos:
Sea el conjunto
; entonces el producto cartesiano A A es:
AxA   1,1, 1,2, , 2,1, (2,2),, (2,5),, (5,1), (5,2),, (5,5) 
Aquí podemos definir las siguientes relaciones:
Son relaciones de A en A, pues: R1  A  A y R2  A  A
1.5
Funciones
Sea R una relación de A en B; R es una función, si y solo si para cada x ∈Dom(R),
existe un único y ∈ B tal que (x,y) ∈ R .
”
 Notación:
Una función se denota por: f: A⟶B, y se lee: f es una función de A en B.
12
Capítulo II:
Leyes de composición interna
2.1
Breve referencia histórica
A comienzos del siglo XIX se difunden los trabajos de Abel (1802-1829) y Galois
(1811-1832) quienes entre otros temas, promovieron el estudio de conceptos generales y
abstractos como el de grupo . Luego, los trabajos de Gauss generalizaron numerosas
estructuras algebraicas independientes de las nociones aritméticas o geométricas.
Por esta razón, el siglo XIX es un período importante en la historia de la
matemática, porque surge una preocupación por una nueva forma de entender la
matemática, es decir la búsqueda de estructuras, que en su momento se llamó matemática
moderna o álgebra moderna y que actualmente se conoce como álgebra abstracta.
La investigación en álgebra abstracta ha revelado la esencia de las declaraciones
lógicas que fundamentan las matemáticas. Históricamente, se ha encontrado que diferentes
estructuras lógicas pueden ser descritas usando el mismo conjunto de axiomas.
El primer tratado formal sobre las estructuras algebraicas o álgebra moderna es l
Moderne Algebra del matemático holandés B.L. van der Waerden, que se publica en 1930.
13
Evariste Galois es el pionero del álgebra moderna. Su trabajo cambió la dirección
del álgebra de resolver ecuaciones algebraicas a explorar la estructura de anillos, cuerpos,
álgebras y conceptos relacionados (Cory, s.f.).
A pesar de sus ventajas, la corriente de la matemática estructural generó ciertas
resistencias en la comunidad matemática.
2.2
Ley de composición interna
Sea E un conjunto no vacío (E≠∅); se llama ley de composición interna (LCI) entre
elementos de E, a toda aplicación "⊺" de una parte A de E x E en E.
Es decir:
⊺∶𝐴⊆𝐸𝑥𝐸 ⟶𝐸
(𝑎; 𝑏) ⟶ 𝑎 ⊺ 𝑏
Gráficamente:
Observación:
Si A=E x E, se dice que la ley está definida sobre todo E.
Nota:
1. 𝑎 ⊺ 𝑏 se lee a compuesto con b.
“
2. Una ley de composición interna (LCI) en A, llamada también operación interna, se puede
representar usando diversos símbolos, como: ⊺,*, ∘ +,⋅, # , entre otros.
Ejemplo:
”
14
 La suma es una operación interna en el grupo de los números naturales, ya que la adición de
dos números naturales resulta en otro número natural.
(𝑎; 𝑏) ⟶ 𝑎 + 𝑏
Por ejemplo,
(7; 2) ⟶ 7 + 2 = 9 ∈ ℕ
(4; 6) ⟶ 4 + 6 = 10 ∈ ℕ
 La adición de dos números, ya sean enteros, racionales o reales, siempre resulta en otro
número del mismo tipo. Esto demuestra que la adición es una operación interna en los
conjuntos de los números enteros (Z), ℚ y ℝ.
Es decir:
Ejemplo:
(−3; 5) ∈ ℤ𝑥ℤ ⟹ −3 + 5 = 2 ∈ ℤ
1
2
(2 ; 3) ∈ ℚ𝑥ℚ ⟹
1
2
2
+ 3=
3+4
6
7
=6 ∈ℚ
(8√2; −5√2) ∈ ℝ𝑥ℝ ⟹ 8√2 + (−5√2) = 3√2 ∈ ℝ
15
 La multiplicación de dos números enteros siempre da como resultado otro número entero, lo
que indica que la multiplicación es una operación interna en el conjunto de los números
enteros (Z).
ℤ𝑥ℤ⟶ℤ
(𝑎; 𝑏) ⟶ 𝑎 ∙ 𝑏
Por ejemplo,
(3; −4) ⟶ 3 ∙ (−4) = −12 ∈ ℤ
(−2; −5) ⟶ (−2) ∙ (−5) = 10 ∈ ℤ
 La multiplicación de números naturales, racionales o reales siempre resulta en un número del
mismo tipo en ℕ, ℤ, ℚ y ℝ., lo que indica que la multiplicación es una operación interna en
estos conjuntos.
Por ejemplo:
(6; 5) ∈ ℕ𝑥ℕ
−3
2
( 4 ; 5) ∈ ℚ𝑥ℚ ⟹
−3
4
⟹ 6 ⋅ 5 = 30 ∈ ℕ
2
⋅ 5=
(−3)⋅(2)
4⋅(5)
−6
−3
= 20 = 10 ∈ ℚ
(3√8; √2) ∈ ℝ𝑥ℝ ⟹ 3√8 ⋅ √2 = 3√16 = 12  ℝ
 La potenciación en el conjunto de los números naturales (ℕ) es una ley de composición
interna, pues para todo par (𝑎; 𝑏) distinto de (0; 0), la potencia 𝑎𝑏 ∈ ℕ.. Esta operación
se define como: 𝑎 ⊺ 𝑏 = 𝑎𝑏 donde (𝑎; 𝑏) ≠ (0; 0)
16
Por ejemplo:
⊺ 4 = 34 = 81 ∈ ℕ
2 ⊺ 5 = 25 = 25 ∈ ℕ
7 ⊺ 0 = 70 = 1 ∈ ℕ
En general, dados (𝑎; 𝑏) en ℕ𝑥ℕ, 𝑎 ⊺ 𝑏 = 𝑎𝑏 ∈ ℕ
 Sea el conjunto 𝐸 = {𝑎, 𝑏, 𝑐} y las operaciones " ∗ " y " ∘ " definidas por:
∗ es una es una ley de composición
interna en 𝐸, porque:
∘ no es una ley de composición interna en
𝐸, porque 𝑏 ∘ 𝑏 = 𝑒, y 𝑒 ∉ 𝐸.
∀𝑥, 𝑦 ∈ 𝐸: 𝑥 ∗ 𝑦 ∈ 𝐸.
 Sea E≠∅; en P(E) , la unión "∪" y la intersección "∩" son leyes de composición
interna; porque por ejemplo: Sea E={a,b} entonces P(E)={∅,{a},{b},E}; luego:
La unión " ∪ " es una LCI en 𝒫(𝐸).
La intersección "∩" es una LCI en 𝒫(𝐸).
 La sustracción no es una operación interna en el conjunto de los números naturales, ya
que la resta de dos números naturales no siempre resulta en un número natural.
17
(8;3)  8  3  5  ℕ
(7;7)  7  7  0  ℕ
(3;10)  3  10  7  ℕ
Solo cuando el número del que se resta (minuendo) es mayor o igual al número que
se resta (sustraendo), la resta de dos números naturales da como resultado otro número
natural. Si el minuendo es menor, el resultado no será un número natural.
Simbólicamente: 𝑎 − 𝑏 ∈ ℕ ⟺ 𝑎 ≥ 𝑏.
 La división no es una operación interna en el conjunto de los números enteros, ya que el
resultado de dividir dos números enteros solo es otro número entero cuando el
dividendo es múltiplo del divisor, en otras palabras el (𝑎; 𝑏) ∈ ℤ𝑥ℤ
𝑎 ÷ 𝑏 ∈ ℤ ⟺ ∃ 𝑐 ∈ ℤ tal que 𝑎 = 𝑐 ∙ 𝑏
Así:
15 ÷ 3 ∈ ℤ, 𝑝𝑢𝑒𝑠 ∃ 𝑐 = 5 ∈ ℤ tal que 15 = 5 ∙ 3, es decir 15 es múltiplo de 3.
8 ÷ 12 ∉ ℤ, pues 8 no es múltiplo de 12.
40 ÷ 6 ∉ ℤ, pues 40 no es múltiplo de 6.
2.3
Leyes asociativas
Dado un conjunto 𝐴 ≠ ∅ y * una ley de composición interna definida en A; se dice
que * es asociativa si y solo si, para todo a,b y c en A, se tiene:
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
Es decir, ∗ es asociativa en 𝐴, si
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐), ∀ 𝑎, 𝑏, 𝑐 ∈ 𝐴.
Ejemplo:
 La adición en el conjunto de los números naturales es asociativa, pues:
(𝑎 + 𝑏) + 𝑐 = 𝑎 + (𝑏 + 𝑐), ∀ 𝑎, 𝑏, 𝑐 ∈ ℕ.
18
Así: (5  3)  6  5  (3  6)
86  59
14  14
 En general, en los conjuntos numéricos ℕ, ℤ, ℚ, y ℝ, las operaciones de adición (+) y
“
multiplicación (⋅) son asociativas, pues para todo a, b, c en estos conjuntos se cumplen
(𝑎 + 𝑏) + 𝑐 = 𝑎 + (𝑏 + 𝑐)
(𝑎 ⋅ 𝑏) ⋅ 𝑐 = 𝑎 ⋅ (𝑏 ⋅ 𝑐)
 El conjunto E y 𝒫(𝐸) todo conjunto de parte de E. En 𝒫(𝐸) toda operación de
intersección (  ) como de unión (  ) es asociativa, pues  A, B, C en 𝒫(𝐸) se cumple
que :
”
 Sea 𝐴 = {𝑎, 𝑏} y ∗ definida por:
Se verifica que:
( x  y)  z  x  ( y  z); x, y, z  A
Por ejemplo:
i. a  b   a  a  (b  a)
ii a  b   b  a  (b  b)
b  a  a b
b b  a  a
bb
aa
19
Por lo tanto ∗ es asociativa en A.
 Todo conjunto de numero entero tiene por definición la operación 𝑎 ∗ 𝑏 = 𝑎𝑏 + 1 para
cualquier par 𝑎, 𝑏 en ℤ.
Se verifica que la operación ∗ no es asociativa, puesto que por ejemplo para 2, 3, 4, en
ℤ:
(2 ∗ 3) ∗ 4 = (2 (3) + 1) ∗ 4 = 7 ∗ 4 = 7 (4) + 1 = 29
2 ∗ ( 3 ∗ 4 ) = 2 ∗ ( 3 (4) + 1) = 2 ∗ 13 = 2 (13) + 1 = 27
Es decir, (2 ∗ 3 ) ∗ 4  2 ∗ ( 3 ∗ 4 )
Entonces ∗ no es asociativa en ℤ.
En general, dados 𝑎, 𝑏, 𝑐 en ℤ no siempre se cumple (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐),
puesto que:
 La siguiente tabla muestra la operación ∗ definida en el conjunto A = {a, b, c }.
Como para 𝑎, 𝑏, 𝑐 en 𝐴 se tiene:
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑐 ∗ 𝑐 = 𝑎
𝑎 ∗ (𝑏 ∗ 𝑐) = 𝑎 ∗ 𝑐 = 𝑏
20
Concluimos que ∗ no es asociativa en 𝐴.
2.4
Elementos permutables
Sea el par (𝐴,∗), decimos que dos elementos 𝑎 𝑦 𝑏 de 𝐴 son permutables si.
𝑎∗𝑏 =𝑏∗𝑎
Ejemplo:
 En ( ℕ, +) 3 y 5 son permutables pues 3 + 5 = 5 + 3.
 Sea A  1;2;3 y ∗ definida por:
2 y 3 son permutables pues 2  3  3  2
11
 A ={ a , b , c , d }como conjunto y las operaciones ∗ y ⊺ definida a través de la
siguiente tabla:
- En la tabla que define la operación ∗ se observa que:
21
pues
ab = ba = b
a permuta con c pues
ac = ca = c
a permuta con d
pues
ad= d a =d
b permuta con d
pues
bd= d b=c
c permuta con
pues
cd= d c =b
a permuta con b
d
- En la tabla que define la operación ⊺ se observa que:
b permuta con c pues
b⊺c = c⊺d =d
c permuta con
c⊺ d =d⊺c = b
d
pues
 En el conjunto ℕ − {0} con la operación de potenciación:
𝑎 ∗ 𝑏 = 𝑎𝑏
- 2 y 4 son permutables, pues
2 * 4 = 24 = 16
4 * 2 = 42 = 16
Es decir, 2 * 4 = 4 * 2
- 1 y 2 no son permutables, pues
1 * 2 = 12 =1
2 * 1 = 21 = 2
Es decir, 1 * 2  2 * 1
 En ( ℚ − {0}; ÷)
- 1 y -1 son permutables pues:
- 7 y -7 son permutables pues:
-
2
3
y
3
2
1
1

1 1
7
−7
= 7 = −1
−7
no son permutables pues:
2
3
3
2
=
4
9
y
3
2
2
3
=
9
4
 En el conjunto de los números enteros se define la operación ∗ para a y b en ℤ:
22
𝑎 ∗ 𝑏 = 𝑎 + 𝑏2
- Dados 1 y 0 en ℤ , tenemos:
1 ∗ 0 = 1 + 02 = 1
0 ∗ 1 = 0 + 12 = 1
Como 1 * 0 = 0 *1, entonces 1 y 0 son permutables.
- Dados ( -1) y 1 en ℤ, tenemos
(-1) * 1 = (-1) + 12 = 0
1 *(-1) = 1 + (-1)2 = 2
Como (-1) * 1  1 * (-1), entonces (-1) y 1 no son permutables.
 Para 3 y 4 en ℤ , se tiene
3 ∗ 4 = 3 + 42 = 19
4 ∗ 3 = 4 + 32 = 13
Entonces
2.5
3 * 4  4 *3, por lo que 3 y 4 no son permutables
Elemento central y centro de un conjunto
Si existe un elemento 𝑐 de 𝐴, que es permutable con todos los elementos de 𝐴, es
decir:
∀ 𝑎 ∈ 𝐴, 𝑎 ∗ 𝑐 = 𝑐 ∗ 𝑎.
Entonces se dice que 𝑐 es un elemento central de 𝐴.
El conjunto 𝜀 de (𝐴,∗) formado por todos los elementos centrales de 𝐴, se llama
centro de 𝐴; es decir:
 = { c  𝐴 / 𝑎 ∗ 𝑐 = 𝑐 ∗ 𝑎, ∀ 𝑎 ∈ 𝐴 }
Ejemplo:
 Si A = { a , b ,c } y la operación definida en A es:
23
“a” es elemento central, pues:
a  a = a  a = a
a  b = b  a
= b
a  c = c  a = c
De igual manera “b y c” son elementos centrales.
 Si B = { x , y , z , t } y la operación definida en B es:
Aquí “x” es elemento central porque es permutable con x, y, z, t. Verifique.
¿Existen otros elementos centrales?
 Si 𝐴 = ℤ, ℚ, ℝ, y " + ", entonces un elemento central de A para la
ley " + " es el cero “0”; pues: 0 + a = a + 0, a  A.
 Análogamente en A con la ley “∙” (multiplicación) “1” es un elemento central porque
1 ∙ a = a ∙ 1, a  A.
Llamamos centro de A y denotamos Cent (A) al conjunto formado por todos los
elementos centrales.
En los ejemplos anteriores:
Cent ( A)  a, b, c
Cent( B)  x
Cent( A1 )  0
24
Cent( A1 )  1 y en cada caso.
Como corolario, podemos afirmar que un conjunto A con una L.C.I. puede tener
uno, dos, tres, o más centros, o ninguno.
2.6
Leyes conmutativas
Mencionado el conjunto 𝐴 ≠ ∅ y ∗ una LCI va definido en A; se menciona que
∗ es conmutativa si:
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎, ∀ 𝑎, 𝑏 ∈ 𝐴.
Es decir, se dice que la ley ∗ es conmutativa en el conjunto 𝐴, si todos sus
elementos son permutables.
Ejemplo:
 La adición en ℤ es conmutativa, pues:
𝑎 + 𝑏 = 𝑏 + 𝑎; ∀ 𝑎, 𝑏 ∈ ℤ
Así:
3 + (−7) = (−7) + 3
−4 = −4
(−15) + (−7) = (−7) + (−15)
−22 = −22
De igual manera, la adición es conmutativa en ℕ, ℚ y ℝ; lo que en lenguaje
coloquial expresamos como “el orden de los sumandos no altera la suma”.
 En general, (ℕ, +), (ℤ, +), (ℚ, +), (ℝ, +) y (ℕ, ⋅), (ℤ, ⋅), (ℚ, ⋅) 𝒚 (ℝ, ⋅), son
conmutativos, pues para todo 𝑎 y 𝑏 en estos conjuntos se cumple:
𝑎+𝑏 =𝑏+𝑎
𝑎⋅𝑏 =𝑏⋅𝑎
25
 Sea 𝐸 = {𝑎, 𝑏, 𝑐} y ∗ definida por:
Se verifica que:
x  y  y  x; x, y  E
Por ejemplo:
a b  b  a
a c  c a
b c  c b
cc
bb
aa
Por lo tanto ∗ es conmutativa en E.
 El monoide (𝒫(𝐸), ∪) es conmutativo.
 La sustracción en ℕ no es conmutativa, pues:
10 − 4 ≠ 4 − 10
6 ≠ −6
 La división en ℤ no es conmutativa, pues:
24 ÷ 6 ≠ 6 ÷ 24
4 ≠
1
4
26
 La potenciación en ℕ no es conmutativa, pues:
3 2 ≠ 23
8 ≠9
2.8
Leyes distributivas
“
Sea A   provisto de dos LCI:  y .
Se dice que la ley  es distributiva con respecto a la ley  si se cumple que:
 x (yz) = (x y)(x  z)
(Distributiva a derecha)
 (y  z)x=(y  x)(z  x )
(Distributiva a izquierda)
x,y,zA
Ejemplo:
 En el conjunto de los números naturales, la multiplicación es distributiva respecto a la
adición.
Pues,  a , b , c ℕ , se cumple:
- a . (b + c) = a . b + a . c
(distributiva a derecha)
- (b + c) . a = b .a + c . a
(distributiva a izquierda)
 Del mismo modo la multiplicación es distributiva respecto a la adición en ℤ, ℚ 𝑦 ℝ
”
 Si en Z 3  0.1, 2 definimos las operaciones.
Aquí se ve que  x , y , z  ℤ3 se cumple que:
x  ( y  z )  ( x  y)  ( x  z )
27
y también:
( x  y)  z  ( x  z )  ( y  z )
En efecto, veamos algunos:
1 . (1 + 2) = 1 . 1 + 1 . 2
0 .( 1 + 2 ) = 0 . 1 + 0 . 2
1 . 0 = 1 + 2
0 . 0 = 0. 0
0 = 0
0 = 0
2 . (1 + 0) = 2 . 1 + 2 . 0
2 . 1 = 2 + 0
1 .( 2 + 0 ) = 1 . 2 + 1 . 0
1 . 2 = 2 . 0
2 =
2 = 0
2
Lo mismo por la derecha.
 En P(E) donde 𝐸 ≠ ∅, la unión () y la intersección () son distributivas
mutuamente pues:
- A  (B  C ) = (A  B )  (A  C)
- A  (B  C) = (A  B)  (A  C)
2.9
Elementos distinguidos y regulares
2.9.1 Elemento neutro
El conjunto 𝐴 ≠ ∅ y ∗ el elemento e  A se llama neutro, si;
𝑎 ∗ 𝑒 = 𝑎  𝑒 ∗ 𝑎 = 𝑎; ∀𝑎 ∈ 𝐴
Observación:
Si 𝑎 ∗ 𝑒 = 𝑎 , 𝑒 es neutro el elemento por la derecha.
Si 𝑒 ∗ 𝑎 = 𝑎 , 𝑒 es neutro el elemento por la izquierda.
28
Ejemplo:
 Todo conjunto de números naturales el cero (0) es elemento neutro cuando viene
provisto de la suma; puesto que 0 ∈ ℕ, además:
𝑎 + 0 = 0 + 𝑎 = 𝑎; ∀𝑎 ∈ ℕ
De manera general, el elemento neutro es el (c) de la adición en ℤ, ℚ, ℝ 𝑦 ℂ.
 En (ℕ, ∙), (ℤ, ∙ ), (ℚ, ∙ ) y (ℝ, ∙) el 1 que es natural, entero, racional, real y complejo,
es elemento neutro, pues:
Ello quiere decir que el 1 es de la multiplicación como el elemento neutro en todo
conjunto de números naturales, racionales, reales y enteros.
𝑎⋅𝑏
 Si en ℚ se define la ley de composición interna 𝑎 ∗ 𝑏 = 4 ; ¿existirá un elemento
neutro?
Mencionemos que “e” es el elemento neutro; entonces
Se puede afirmar que el elemento neutro 𝑒 = 4 ya que el neutro de la derecha e
izquierda son iguales.
2.9.2 Elemento simétrico
Sea un conjunto A≠∅ y * una ley de composición interna definida en A con
elemento neutro e.
29
En este caso a∈A , hay un elemento a^´∈A , debido a que:
a*a´=e
a´*a=e; ∀a∈A
Observación:
 Se dice que a^´ es el elemento simétrico de a.
 Si a*a´=e , a´ toma por nombre elemento simétrico de a por la derecha.
“
 Si a´*a=e , a´ toma por nombre elemento simétrico de a por la izquierda.
Ejemplo:
 En el par ( Z; +) el elemento neutro es 0, el elemento simétrico de 5 es -5, puesto que
En general el opuesto de
Z es
Z, puesto que:
(a)  (a)  (a)  (a)  0
 En el conjunto ℤ con la multiplicación, el elemento neutro es 𝑒 = 1.
”
Para 𝑎 ∈ ℤ, si 𝑎−1 ∈ ℤ, entonces 𝑎 = 1 ∨ 𝑎 = −1.
Es decir, en ℤ, 1 y (-1) son los únicos elementos inversibles, puesto que:
Si 𝑎 = 1  1-1 = 1 , es decir, 1 ⋅ 1−1 = 1−1 ⋅ 1 = 1
1⋅1=1
Si 𝑎 = −1  (−1)−1 = −1 , es decir, (−1) ⋅ (−1)−1 = (−1)−1 ⋅ (−1) = 1
 (−1) ⋅ (−1) = 1
Si 𝑎 = 5 en ℤ, a-1 = 5-1  ℤ, es decir 5 no es inversible en ℤ, respecto a la
multiplicación, pues no existe 𝑑 en ℤ tal que
d.5=1

 En ( ℝ − {0}; ∙ )
El inverso de 2/5 es 5/2, pues:
2 5 5 2
   1
5 2 2 5
5. d = 1
30
 Si en ℝ da por concepto la operación a  b  a 2  b 2 .
Es posible encontrar el neutro y el elemento simétrico, si existen.
 Para poder ubicar el elemento neutro, suponemos que el neutro es e  ℝ.
Por ende es verificable que:
a e  a

ea  a
a 2  e2  a
e2  a 2  a
a 2  e2  a 2
e2  a 2  a 2
e2  0
e2  0
e0
e0
Entonces el elemento neutro de (ℝ ,  ) es e  0.
 Para ubicar el elemento simétrico:
a  a'  e

a'  a  e
a 2  (a' ) 2  0
(a' ) 2  a 2  0
a 2  ( a' ) 2  0
( a' ) 2  a 2  0
(a' )2  0
(a' )2  0
a' 0
a' 0
Luego, en (ℝ ,  ) el elemento simétrico de a es a  0.
2.9.3 Elemento absorbente
Sea el par (𝐴, ∗), un elemento 0̃ de 𝐴 se denomina elemento absorbente de 𝐴, si:
0̃ ∗ 𝑎 = 𝑎 ∗ 0̃ = 0̃, ∀𝑎 ∈ 𝐴
31
Ejemplo:
 En todo conjunto de numero natural con la multiplicación como operación el elemento
absorbente es el cero (0), pues el producto de todo número natural por cero (0) es cero
(0).
Es decir, 0 ∗ 𝑎 = 𝑎 ∗ 0 = 0, ∀𝑎 ∈ ℕ.
 En forma general el cero (0) es el elemento absorbente de la multiplicación en el
conjunto de los números enteros, racionales y reales; pues para cualquier número
entero, racional o real, se cumple que: 0 ⋅ 𝑎 = 𝑎 ⋅ 0 = 0.
 En (ℕ, +), ¿existirá elemento absorbente?
No existe.
Pues, suponiendo que fuera 0̃ se tendría 0̃ + 𝑎 = 0̃, ∀𝑎 ∈ 𝐴 , lo que es falso.
 En (ℝ − {0}, ∗) se define la operación ∗ como: 𝑎 ∗ 𝑏 = +𝑏 − 𝑎𝑏, halle el elemento
absorbente si existe.
- Si existe el elemento absorbente, supongamos que es 0̃.
Entonces se debe cumplir que: 0̃ ∗ 𝑎 = 0
Luego por definición de ∗ se tiene:
Es decir, el elemento absorbente a izquierda es 1.
- Ahora supongamos que 0̃ es el elemento absorbente a derecha.
Entonces se debe cumplir que: 𝑎 ∗ 0̃ = 0
Luego por definición de ∗ se tiene:
𝑎 ∗ 0̃ = 𝑎 + 0̃ − 𝑎 ∙ 0̃ = 0̃
32
Luego, 𝑎 ∙ 0̃ = 𝑎
De donde:
0̃ = 1
Es decir, el elemento absorbente a derecha también es 1, por lo tanto el elemento
absorbente es 1.
2.9.4 Elementos regulares
Sea el par (𝐴, ∗) y 𝑎 un elemento de 𝐴; decimos que 𝑎 es un elemento regular
respecto a la ley ∗ si y solo si:
Es decir, 𝑎 ∈ 𝐴 si es regular a izquierda y a derecha, es un elemento regular de 𝐴.
Ejemplo:
 Inspeccionar si en (ℚ, ∗) en el que: 𝑥 ∗ 𝑦 = 𝑥 + 𝑦 + 𝑥 ∙ 𝑦, existen elementos regulares.
Dado x , y , z  ℚ , en el que probaremos que:
En efecto:
x + y + x.y = x + z + x. z

y + x + y. x
= z + x + z. x
y (1 + x ) = z (1 + x )
y (1 + x) = z (1 + x )
y=z
y=z
Para 𝑥 ≠ −1; es decir, todo numero racional diferente de -1 es regular
 En (ℝ, ⋅) todo número real a excepción del cero son regulares, en este caso:
Si 𝑎 ⋅ 𝑏 = 𝑎 ⋅ 𝑐
⟹ 𝑏 = 𝑐 pues a  0
Si 𝑏 ⋅ 𝑎 = 𝑐 ⋅ 𝑎
⟹ 𝑏 = 𝑐 pues a  0
33
Capítulo III.
Estructuras algebraicas
3.1
Estructura algebraica
“
Una estructura algebraica es un conjunto no vacío que se rige por una o más reglas
de composición.
Las estructuras algebraicas se representan generalmente como (A,*,°,⊺,#,…), donde
A es un conjunto no vacío y *,°,⊺,#,… son las leyes establecidas en ese conjunto.
3.2
Monoides
Todo conjunto 𝐴 ≠ ∅ , que tenga LCI “∗” es llamado monoide, ello es
”
representado como (𝐴;∗).
Los conjuntos de números naturales, enteros, racionales y reales, cuando se les
aplica la operación de adición o multiplicación, son monoides. Esto se debe a que estas
operaciones son leyes de composición interna en estos conjuntos.
El conjunto de polinomios de grado n también es un monoide bajo la operación de
adición, ya que la suma de polinomios de grado n es una ley de composición interna.
34
Finalmente, el conjunto de todas las funciones de R en R, denotado como F®, es un
monoide bajo la operación de composición de funciones, ya que la composición de dos
funciones reales resulta en otra función real.
3.3
Semigrupos
Todo conjunto 𝐴 ≠ ∅ que va de la mano con la ley de composición interna ∗ y es
asociativa lleva por nombre semigrupo.
Es decir, (𝐴,∗) es un semigrupo, si
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐), ∀ 𝑎, 𝑏, 𝑐 ∈ 𝐴.
Ejemplo:
 (ℕ, +) es un semigrupo, pues:
(𝑎 + 𝑏) + 𝑐 = 𝑎 + (𝑏 + 𝑐), ∀ 𝑎, 𝑏, 𝑐 ∈ ℕ.
Así:
(2  3)  7  2  (3  7)
5  7  2  10
10  10
 Son semigrupos:
- (ℕ, +), (ℤ, +), (ℚ, +), (ℝ, +) y (ℂ, +)
- (ℕ,⋅), (ℤ,⋅), (ℚ,⋅), (ℝ,⋅) y (ℂ,⋅)
Puesto que la adición (+) y la multiplicación (⋅) son operaciones asociativas en los
“
conjuntos ℕ, ℤ, ℚ, ℝ y ℂ.
 (𝒫(𝐸), ∩) y (𝒫(𝐸), ∪) son semigrupos pues la intersección () y la reunión () de
conjuntos son operaciones asociativas en 𝒫(𝐸) .
”
35
 Sea
A  a; b y ∗ definida por:
Es verificable que:
Podemos decir que:
3.4
Grupos
Sea el conjunto 𝐺 ≠ ∅ y " ∗ " una LCI definida en el conjunto 𝐺, se conoce que
el monoide (𝐺, ∗) su estructura es de grupo si es verificable los siguientes axiomas:
𝐺1 : La ley ∗ es asociativa
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐), ∀ 𝑎, 𝑏, 𝑐 ∈ 𝐺
𝐺2 : (𝐺, ∗) tiene elemento neutro.
∃𝑒 ∈𝐺/ 𝑎∗𝑒 =𝑒∗𝑎 =𝑎; ∀𝑎 ∈ 𝐺
𝐺3 : Existencia de elemento simétrico.
∃ 𝑎´ ∈ 𝐺 / 𝑎 ∗ 𝑎´ = 𝑎´ ∗ 𝑎 = 𝑒 ; ∀ 𝑎 ∈ 𝐺
Además
𝐺4 : La ley ∗ es conmutativa.
𝑎∗𝑏 =𝑏∗𝑎; ∀𝑎 ∈𝐺
36
El grupo (𝐺, ∗) es un grupo conmutativo o grupo abeliano.
Ejemplo:
 Todo conjunto de numero entero que va provisto de la adición como operación, (ℤ, +),
es un grupo conmutativo o grupo abeliano.
Puesto que:
+: ℤ𝑥 ℤ ⟶ ℤ
(𝑎; 𝑏) = 𝑎 + 𝑏
Además, se cumplen los siguientes axiomas:
𝐺1 : La adición de números enteros es asociativa.
(𝑎 + 𝑏) + 𝑐 = 𝑎 + (𝑏 + 𝑐), ∀ 𝑎, 𝑏, 𝑐 ∈ ℤ
Así, por ejemplo, tomando los números enteros −7, 3 𝑦 5, se cumple:
(−7 + 3) + 5 = −7 + (3 + 5)
−4 + 5 = −7 + 8
1=1
𝐺2 : Existencia del elemento neutro.
Pues ∃ 0 ∈ ℤ / 𝑎 + 0 = 0 + 𝑎 = 𝑎 ; ∀ 𝑎 ∈ ℤ
Así, dado el número entero −2 se tiene:
−2 + 0 = 0 + (−2)
−2 = −2
𝐺3 : Existencia del elemento simétrico.
∀ 𝑎 ∈ ℤ, ∃ − 𝑎 ∈ ℤ / 𝑎 + (−𝑎) = (−𝑎) + 𝑎 = 0 ;
Por ejemplo, si tomamos el número entero 7, se tiene el número entero −7 tal que:
7 + (−7) = (−7) + 7
0=0
De igual manera, si tomamos el número entero −8 se tiene:
37
−8 + 8 = 8 + (−8)
0=0
Además:
𝐺4 : La adición de números enteros es conmutativa.
Así, dados los números enteros 6 y −9 se tiene:
6 + (−9) = (−9) + 6
−3 = −3
Por lo tanto, (ℤ, +) es un grupo abeliano.
 El par (ℤ,  ) en el que ℤ es conjunto de todo número entero y  es una ley de
composición interna que tiene por definición como a  b = a + b + 3, es un grupo
abeliano.
-  es una ley de composición interna en ℤ , pues:
Si a y b  ℤ, (a + b + 3)  ℤ puesto que la adición es una LCI en ℤ.
-  es asociativa, dado que
y
- Existe un elemento neutro, puesto que, ∀a ∈ ℤ:
y
- Todo elemento a ∈ ℤ tiene inverso, ya que:
es inverso a la derecha
es inverso a la izquierda
38
- Finalmente,  es conmutativa pues,
 En ℝ+ se define la operación x  y = 5 x y.
¿Será el monoide (ℝ+ , ∗) un grupo abeliano?
- Asociatividad
 x , y , z  ℝ+ , ( x  y )  z = (5 x y)  z
= 5 (5 x y). z
= (5x y) . 5z
= (5x) y 5z
= (5x) (5yz)
=
5 (x . (5 y . z ) )
=
x  (5 y . z )
= x  (yz)
- Existencia del elemento neutro
Supongamos que el neutro es 𝑒 ∈ ℝ+ , entonces:
e  x = x
∧
x  e = x
5ex = x
∧
5 x e = x
e = 1/5
e = 1/5
Se observa que es neutro a izquierda y derecha.
1
Por lo que concluimos que existe neutro y que es: 𝑒 = 5 .
- Existencia del elemento simétrico
De manera similar al caso anterior, supongamos que el simétrico de x ℝ+ , es x´
 ℝ+ , entonces debe ser simétrico a izquierda y derecha.
Entonces:
x´  x = e

x  x´ = e
39
5 x´ . x = 1 / 5
5 x . x´ = 1 / 5
1
1
𝑥´ = 25 𝑥
𝑥´ = 25 𝑥
Se observa que los simétricos a izquierda y derecha existen y son iguales; luego,
el simétrico es: x´ = 1 / 25 x
- ¿Es abeliano?
x  y = 5 x y = 5 y x = y  x ,  x , y  ℝ+ .
 (ℝ+ , ∗) es un grupo abeliano.
 Sea 𝐴 = {𝑎, 𝑏} y la operación " ∗ " definida por:
Verificar si (𝐴,∗) es un grupo abeliano.
𝐺1 : La ley ∗ es asociativa
Pues: (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐), ∀ 𝑎, 𝑏, 𝑐 ∈ 𝐴
Así tenemos a partir de los elementos de la tabla adjunta:
(𝑎 ∗ 𝑏) ∗ 𝑎 = 𝑎 ∗ (𝑏 ∗ 𝑎)
𝑏∗𝑎 =𝑎∗𝑏
𝑏=𝑏
(𝑎 ∗ 𝑎) ∗ 𝑏 = 𝑎 ∗ (𝑎 ∗ 𝑏)
𝑎∗𝑏 =𝑎∗𝑏
𝑏=𝑏
𝐺2 : Existencia del elemento neutro.
∃𝑒 ∈𝐴/ 𝑎∗𝑒 =𝑒∗𝑎 =𝑎; ∀𝑎 ∈𝐴
40
Así:
𝑎∗𝑒=𝑎
∧
𝑒∗𝑎 =𝑎
𝑒=𝑎
𝑏∗𝑒=𝑏
𝑒=𝑎
∧
𝑒∗𝑏 =𝑏
𝑒=𝑎
𝑒=𝑎
𝐺3 : Existencia de elementos simétricos.
∃ 𝑎´ ∈ 𝐴 / 𝑎 ∗ 𝑎´ = 𝑎´ ∗ 𝑎 = 𝑒 ; ∀ 𝑎 ∈ 𝐴
Para 𝑎:
𝑎 ∗ 𝑎 = 𝑎 ∗ 𝑎 = 𝑎 luego, 𝑎´ = 𝑎
Para 𝑏:
𝑏 ∗ 𝑏 = 𝑏 ∗ 𝑏 = 𝑎 luego, 𝑏´ = 𝑏
Además:
𝐺4 : La ley ∗ es conmutativa.
𝑎∗𝑏 =𝑏∗𝑎
𝑏=𝑏
Luego, por 𝐺1 , 𝐺2 , 𝐺3 y 𝐺4 , (𝐴, ∗) es un grupo abeliano
3.5
Subgrupos
Sea (𝐺; ∗) un grupo, y un subconjunto no vacío 𝐻 del conjunto 𝐺. Mencionamos
que 𝐻 es un subgrupo de 𝐺, si (𝐻; ∗) es un grupo.
41
∗ ∶ 𝐻𝑥𝐻 ⟶ 𝐻
(𝑎; 𝑏) ⟶ 𝑎 ∗ 𝑏
Es decir:
Dado el grupo (𝐺; ∗) y ∅ ≠ H ⊂ G
(𝐻; ∗) es un subgrupo de (𝐺; ∗) ⟺ (𝐻; ∗) es un grupo.
Ejemplo:
 Como (ℚ; +) es un grupo, y ℤ ⊂ ℚ; (ℤ , + ) es un subgrupo de (ℚ , + ).
 Dado el grupo abeliano (ℤ, + ).
Sea:
2ℤ = {… , −8. −6. −4, −2, 0, 2, 4, 6, 8, … } un subconjutno de ℤ.
Se verifica que (2ℤ, + ) es un grupo de (ℤ, + ); pues:
𝐺1 : Es asociativa.
(𝑎 + 𝑏) + 𝑐 = 𝑎 + (𝑏 + 𝑐), ∀ 𝑎, 𝑏, 𝑐 ∈ 2ℤ
Así:
(−6 + 4) + 10 = −6 + (4 + 10)
−2 + 10 = −6 + 14
8 =8
𝐺2 : Existe elemento neutro.
Pues ∃ 0 ∈ 2ℤ / 𝑎 + 0 = 0 + 𝑎 = 𝑎 ; ∀ 𝑎 ∈ 2ℤ
Así, dado el número entero −6 se tiene:
−6 + 0 = 0 + (−6)
−6 = −6
𝐺3 : Existencia del elemento simétrico (opuesto aditivo).
∀ 𝑎 ∈ 2ℤ, ∃ − 𝑎 ∈ 2ℤ / 𝑎 + (−𝑎) = (−𝑎) + 𝑎 = 0 ;
Por ejemplo, si tomamos el número 12, se tiene el número entero −12 tal que:
42
12 + (−12) = (−12) + 12
0=0
Además:
𝐺4 : La adición en 2ℤ es conmutativa.
𝑎 + 𝑏 = 𝑏 + 𝑎 ; ∀ 𝑎 ∈ 2ℤ
Así, dados los números −6 y 24 se tiene:
−6 + 24 = 24 + (−6)
18 = 18
Así se verifica que (2ℤ, +) es un grupo; y como 2ℤ ⊂ ℤ , entonces decimos que
(2ℤ, +) es un subgrupo de (ℤ, +).
3.6
Homomorfismo de grupos
Dados los grupos (𝐺; ∗) y (𝐺´; ∘), la función 𝑓: 𝐺 ⟶ 𝐺´ es un homomorfismo si
y solo si, la imagen de la composición en 𝐺 es igual a la composición de las imágenes en
𝐺´.
Es decir,
𝑓: 𝐺 ⟶ 𝐺´ es homomorfismo ⟺ 𝑓(𝑎 ∗ 𝑏) = 𝑓(𝑎) ∘ 𝑓(𝑏)
Gráficamente:
43
Ejemplo:
 Demostrar que la función 𝑓: ℝ ⟶ ℝ, definida por: 𝑓(𝑥) = 𝑎𝑥, donde 𝑎 es un número
real fijo, es un homomorfismo entre los grupos (ℝ, +) y (ℝ, +).
En efecto, para todo 𝑥, 𝑦 ∈ ℝ se verifica que:
𝑓(𝑥 + 𝑦) = 𝑎(𝑥 + 𝑦) = 𝑎𝑥 + 𝑎𝑦 = 𝑓(𝑥) + 𝑓(𝑦)
 Dada la función 𝑓: ℝ ⟶ ℝ, definida por: 𝑓(𝑥) = 𝑎 𝑥 ; con 𝑎 > 0 un número real fijo.
Demostrar que 𝑓 es un homomorfismo entre los grupos (ℝ, +) y (ℝ − {0}, ∙).
En efecto, para todo 𝑥, 𝑦 ∈ ℝ se verifica:
𝑓(𝑥 + 𝑦) = 𝑎 𝑥+𝑦 = 𝑎 𝑥 ∙ 𝑎 𝑦 = 𝑓(𝑥) ∙ 𝑓(𝑦)
 Sea la función 𝑓: ℝ ⟶ ℝ, definida por: 𝑓(𝑥) = 𝑎 + 𝑥; donde 𝑎 es un número real fijo.
Analizar si 𝑓 es homomorfismo entre los grupos (ℝ, +) y (ℝ, +).
Debemos analizar si se verifica que: 𝑓(𝑥 + 𝑦) = 𝑓(𝑥) + 𝑓(𝑦), todo 𝑥, 𝑦 ∈ ℝ.
Según la definición de la función 𝑓 , tenemos:
𝑓(𝑥 + 𝑦) = 𝑎 + (𝑥 + 𝑦)
𝑓(𝑥) + 𝑓(𝑦) = (𝑎 + 𝑥) + (𝑎 + 𝑦)
Ahora,
𝑓(𝑥 + 𝑦) = 𝑓(𝑥) + 𝑓(𝑦) ⟺ 𝑎 + 𝑥 + 𝑦 = 2𝑎 + 𝑥 + 𝑦 ⟺ 𝑎 = 2𝑎 ⟺ 𝑎 = 0
Es decir, 𝑓 es homomorfismo entre los grupos (ℝ, +) y (ℝ, +), si y solo si 𝑎 = 0.

Sea ℝ+ el conjunto de los números reales positivos. Dada la función 𝑓: ℝ+ ⟶ ℝ,
definida por: 𝑓(𝑥) = 𝑙𝑜𝑔𝑥; demostrar que 𝑓, es homomorfismo entre los grupos
(ℝ+ , ∙) y (ℝ, +).
Para todo 𝑥, 𝑦 ∈ ℝ+ se cumple que:
𝑓(𝑥 ∙ 𝑦) = log(𝑥 ∙ 𝑦) = 𝑙𝑜𝑔𝑥 + 𝑙𝑜𝑔𝑦 = 𝑓(𝑥) + 𝑓(𝑦)
Así queda verificado que 𝑓es un homomorfismo entre los grupos (ℝ+ , ∙) y
(ℝ, +).
44
 Sean los grupos aditivos (ℝ2𝑥2 , +) y (ℝ2 , +).
La función 𝑓: ℝ2𝑥2 ⟶ ℝ2 definida por:
𝑎
𝑓 ([
𝑐
𝑏
]) = (𝑎 + 𝑑, 𝑏 − 𝑐)
𝑑
Probar que la función 𝑓 es un homomorfismo entre los grupos (ℝ2𝑥2 , +) y
(ℝ2 , +).
𝑚
𝑏
] y 𝐵 = [𝑝
𝑑
𝑎
Sean las matrices 𝐴 = [
𝑐
𝑛
2𝑥2
𝑞 ] elementos de ℝ .
Debemos demostrar que: 𝑓(𝐴 + 𝐵) = 𝑓(𝐴) + 𝑓(𝐵)
En efecto;
𝑎
𝑓(𝐴 + 𝐵) = 𝑓 ([
𝑐
= 𝑓 ([
𝑚
𝑏
] + [𝑝
𝑑
𝑎+𝑚
𝑐+𝑝
𝑛
𝑞 ])
Por sustitución
𝑏+𝑛
])
𝑑+𝑞
Adición en ℝ2𝑥2
= ((𝑎 + 𝑚) + (𝑑 + 𝑞), (𝑏 + 𝑛) − (𝑐 + 𝑝))
Definición de 𝑓 y
cerradura de la adición
en ℝ.
= ((𝑎 + 𝑑) + (𝑚 + 𝑞), (𝑏 − 𝑐) − (𝑛 − 𝑝)) Asociativa de la adición en
ℝ
= (𝑎 + 𝑑, 𝑏 − 𝑐) + (𝑚 + 𝑞, 𝑛 − 𝑝)
Adición en ℝ2
𝑚
𝑏
]) + 𝑓 ([ 𝑝
𝑑
Definición de 𝑓
= 𝑓 ([
𝑎
𝑐
𝑛
𝑞 ])
= 𝑓(𝐴) + 𝑓(𝐵)
Por lo tanto, 𝑓(𝐴 + 𝐵) = 𝑓(𝐴) + 𝑓(𝐵)
igualdad.
Luego, 𝑓 es un homomorfismo
Transitividad de la
45
3.7
Anillos
“
Sea el conjunto 𝐴 no vacío, y dos leyes de composición interna ∗ y ∘; la terna
(𝐴; ∗; ∘) es un anillo, si y solo si se cumplen las siguientes tres condiciones:
- (𝐴; ∗) es un grupo abeliano.
- (𝐴; ∘) es un semigrupo.
- La segunda ley (∘) es distributiva respecto a la primera (∗).
Reemplazando estas dos leyes de composición interna con las leyes aditiva (+) y
multiplicativa ( ∙ ) respectivamente, podemos decir:
La terna (𝐴, +, ∙) es un anillo si y solo si:
- (𝐴; +) es un grupo abeliano.
- (𝐴; ∙) es un semigrupo.
- La multiplicación es distributiva respecto a la adición.
Es otras palabras, (𝐴, +, ∙) es un anillo si cumple los siguientes axiomas:
𝐴1 ∶ Ley asociativa respecto a +
∀ 𝑎, 𝑏, 𝑐 ∈ 𝐴: 𝑎 + (𝑏 + 𝑐) = ( 𝑎 + 𝑏) + 𝑐
𝐴2 ∶ Existencia del elemento neutro respecto a +
∃0∈𝐴/𝑎 +0= 0+ 𝑎;
∀ 𝑎∈𝐴
𝐴3 ∶ Ley del opuesto aditivo.
∀ 𝑎 ∈ 𝐴,
∃ − 𝑎 ∈ 𝐴 / 𝑎 + (−𝑎) = (−𝑎) + 𝑎 = 0
𝐴4 ∶ Ley conmutativa respecto a +
”
∀ 𝑎 ∈ 𝐴, ∀ 𝑏 ∈ 𝐴: 𝑎 + 𝑏 = 𝑏 + 𝑎
𝐴5 ∶ Ley asociativa respecto a ∙
∀ 𝑎, 𝑏, 𝑐 ∈ 𝐴: 𝑎 ∙ (𝑏 ∙ 𝑐) = ( 𝑎 ∙ 𝑏) ∙ 𝑐
𝐴6 ∶ Ley distributiva de la ∙ respecto a la +
46
∀ 𝑎, 𝑏, 𝑐 ∈ 𝐴:
𝑎 ∙ (𝑏 + 𝑐) = 𝑎 ∙ 𝑏 + 𝑎 ∙ 𝑐
{
(𝑏 + 𝑐) ∙ 𝑎 = 𝑏 ∙ 𝑎 + 𝑐 ∙ 𝑎
3.7.1 Anillo conmutativo
Dado el anillo (𝐴, +, ∙) , si la ley multiplicativa ( ∙ ) es conmutativa, decimos que
(𝐴, +, ∙) es un anillo conmutativo.
Es decir, si se cumple que:
𝑎 ∙ 𝑏 = 𝑏 ∙ 𝑎 , ∀ 𝑎, 𝑏 ∈ 𝐴.
3.7.2 Anillo con identidad
Dado el anillo (𝐴, +, ∙), si existe elemento neutro par la ley multiplicativa ( ∙ ),
decimos que (𝐴, +, ∙) es un anillo con identidad o con unidad.
Es decir, se cumple que:
∀ 𝑎 ∈ 𝐴, 1 ∈ 𝐴 ∕ 𝑎 ∙ 1 = 1 ∙ 𝑎 = 𝑎
 Todo conjunto de números enteros que va provisto de la operación de multiplicación y
adición que son usuales, (ℤ, +, ∙), es un anillo conmutativo con unidad.
Puesto que:
- (ℤ, +) es un grupo.
Pues la adición de números enteros es una ley de composición interna, es asociativa
y conmutativa, tiene elemento neutro que es el 0, y cada número entero 𝑎 tiene un
opuesto aditivo que representamos por −𝑎.
-
(ℤ, ∙) es un semigrupo, pues la multiplicación de números enteros es asociativa.
Además es conmutativa y tiene elemento neutro que es el 1.
- La multiplicación de números enteros es distributiva por izquierda y derecha
respecto a la adición.
∀ 𝑎, 𝑏, 𝑐 ∈ ℤ:
𝑎 ∙ (𝑏 + 𝑐) = 𝑎 ∙ 𝑏 + 𝑎 ∙ 𝑐
∧
(𝑏 + 𝑐) ∙ 𝑎 = 𝑏 ∙ 𝑎 + 𝑐 ∙ 𝑎
47
Así:
Distributiva por izquierda:
3 ∙ (−2 + 8) = 3 ∙ −2 + 3 ∙ 8
3 ∙ 6 = −6 + 24
18 = 18
Distributiva por derecha: (−2 + 8) ∙ 3 = −2 ∙ 3 + 8 ∙ 3
6 ∙ 3 = −6 + 24
18 = 18
Por i), ii) y iii), (ℤ, +, ∙) es un anillo conmutativo con unidad.
 Todo conjunto de números racionales que van provisto de la multiplicación y adición
usualmente, (ℚ , +, ∙), es un anillo conmutativo con unidad.
Pues:
-
(ℚ , +) es un grupo abeliano.
En primer lugar, la adición de números racionales es una ley de composición
interna, pues la suma de dos números racionales es un número racional.
Es decir, ∀ 𝑎, 𝑏 ∈ ℚ: (𝑎 + 𝑏) ∈ ℚ
3
1
3
1
5
Así, dados los números racionales 4 y 2 se tiene: 4 + 2 = 4 ∈ ℚ
La adición de números racionales es asociativa, es decir:
(𝑎 + 𝑏) + 𝑐 = 𝑎 + (𝑏 + 𝑐);
1
Así, dados los números racionales 4 ,
1
3
∀ 𝑎, 𝑏, 𝑐 ∈ ℚ
1
y 2 se tiene:
1 1
1 1
1 1
( + )+ = +( + )
4 3
2 4
3 2
7 1 1 5
+ = +
12 2 4 6
13 13
=
12 12
48
- Existe elemento neutro:
∃ 0 ∈ ℚ / 0 + 𝑎 = 𝑎 + 0 = 𝑎; ∀ 𝑎 ∈ ℚ
3
Así, dado el número racional 8 se tiene:
0+
3 3
3
= +0=
8 8
8
- Existe opuesto aditivo:
∀ 𝑎 ∈ ℚ, ∃ − 𝑎 ∈ ℚ / 𝑎 + (−𝑎) = (−𝑎) + 𝑎 = 0
5
5
Así, dado el número racional 6 existe el número racional − 6 tal que:
5
5
5
5
+ (− ) = (− ) + = 0
6
6
6
6
La adición de números racionales es conmutativa:
𝑎 + 𝑏 = 𝑏 + 𝑎; ∀ 𝑎, 𝑏 ∈ ℚ
2
1
Así, dados los números racionales 5 y 3 se tiene:
2 1 1 2
+ = +
5 3 3 5
11 11
=
15 15
-
(ℚ, ∙) es un semigrupo.
En primer lugar, la multiplicación de números racionales es una ley de
composición interna, pues el producto de dos números racionales es siempre un número
racional.
Es decir, ∀ 𝑎, 𝑏 ∈ ℚ: 𝑎 ∙ 𝑏 ∈ ℚ
3
1
3 1
3
Así, dados los números racionales 4 y 2 se tiene: 4 ∙ 2 = 8 ∈ ℚ
La multiplicación de números racionales es asociativa.
(𝑎 ∙ 𝑏) ∙ 𝑐 = 𝑎 ∙ (𝑏 ∙ 𝑐);
3
Así, dados los números racionales 4 ,
1
3
∀ 𝑎, 𝑏, 𝑐 ∈ ℚ
1
y 5 se tiene:
49
3 1 1 3 1 1
( ∙ )∙ = ∙( ∙ )
4 3 5 4 3 5
1 1 3 1
∙ = ∙
4 5 4 15
1
1
=
20 20
La multiplicación de números racionales es conmutativa.
𝑎 ∙ 𝑏 = 𝑏 ∙ 𝑎;
∀ 𝑎, 𝑏 ∈ ℚ
2
1
2
1
1
2
Así, dados los números racionales − 3 y 2 se tiene: (− 3) ∙ 2 = 2 ∙ (− 3)
−
1
1
=−
3
3
La multiplicación de números racionales tiene elemento neutro.
∃ 1 ∈ ℚ / 1 ∙ 𝑎 = 𝑎 ∙ 1 = 𝑎; ∀ 𝑎 ∈ ℚ
3
Así, dado el número racional 5 se tiene:
3
3
3
1∙8=8∙1=8
- Además la multiplicación de números racionales es distributiva respecto a la adición
por izquierda y derecha.
∀ 𝑎, 𝑏, 𝑐 ∈ ℚ:
𝑎 ∙ (𝑏 + 𝑐) = 𝑎 ∙ 𝑏 + 𝑎 ∙ 𝑐
∧ (𝑏 + 𝑐) ∙ 𝑎 = 𝑏 ∙ 𝑎 + 𝑐 ∙ 𝑎
Así:
Distributiva por izquierda:
2
−3
1
2 −3
2 1
∙ ( 4 + 6) = 5 ∙ 4 + 5 ∙ 6
5
2 −7 −3 1
∙
=
+
5 12 10 15
−7 −7
=
30
30
50
Distributiva por derecha:
−3
1
2
−3
2
−3
−7
−7
2
1 2
( 4 + 6) ∙ 5 = 4 ∙ 5 + 6 ∙ 5
−7
12
30
= 30
Por lo tanto, (ℚ , +, ∙) es un anillo conmutativo con unidad.
 Verificar que la terna (ℤ2 , ⨁, ⊚) es un anillo.
- (ℤ2 , ⨁) es un grupo abeliano.
Es asociativa:
(0 ⊕ 1) ⊕ 0 = 0 ⊕ (1 ⊕ 0)
1⊕0= 0⊕1
1=1
(1 ⊕ 1) ⊕ 0 = 1 ⊕ (1 ⊕ 0)
0⊕0= 1⊕1
0=0
Existe elemento neutro:
El elemento neutro es 𝑒 = 0 porque 0 ⊕ 1 = 1 ⊕ 0 = 1
Existe elemento simétrico:
0´ = 0 pues 0 ⊕ 0 = 0
1´ = 1 pues 1 ⊕ 1 = 0
1
∙ 5 = 10 + 15
51
Es conmutativa:
0 ⊕1=1 ⊕0
1=1
Por lo tanto, (ℤ2 , ⨁) es un grupo abeliano.
(ℤ2 , ⊚) es un semigrupo.
Pues es asociativa:
(1 ⊚ 1) ⊚ 1 = 1 ⊚ (1 ⊚ 1)
1⊚1= 1⊚1
1=1
(0 ⊚ 1) ⊚ 1 = 0 ⊚ (1 ⊚ 1)
0⊚1= 0⊚1
0=0
También es conmutativa:
0⊚1= 1⊚0
0=0
Además tiene elemento neutro 𝑒 = 1 :
0⊚1= 1⊚0= 0
1⊚1= 1
-
⊚ es distributiva respecto a ⨁.
Por izquierda: 1 ⊚ (0 ⊕ 1) = (1 ⊚ 0) ⊕ (1 ⊚ 1)
1⊚1= 0⊕1
1=1
Por derecha: (0 ⊕ 1) ⊚ 1 = (0 ⊚ 1) ⊕ (1 ⊚ 1)
1⊚1= 0⊕1
52
1=1
Por lo tanto (ℤ2 , ⨁, ⊚) es un anillo conmutativo con unidad.
3.8
Cuerpos
Todo conjunto 𝐾 ≠ ∅ que tiene una composición interna provisto de dos leyes " +
" y " ⋅ ", se dice que la terna (𝐾; +; ⋅) es un cuerpo, si y solo si:
(𝐾; +) es un grupo abeliano.
(𝐾 − {0}; ⋅) es un grupo.
La ley " ⋅ " es distributiva respecto a la ley " + ".
Se tiene por definición:
(𝐾; +; ⋅) es un cuerpo, si:
(𝐾; +; ⋅) es un anillo.
 En (𝐾 − {0}; ⋅) existe un elemento neutro y todo elemento no nulo tiene inverso.
Estas condiciones se traducen en los siguientes axiomas:
k.1 Asociativa: ∀ 𝑎, 𝑏, 𝑐 ∈ 𝐾: (𝑎 + 𝑏) + 𝑐 = 𝑎 + (𝑏 + 𝑐)
k.2 Existe elemento neutro: ∃0 ∈ 𝐾 ; ∀𝑎 ∈ 𝐾/ 𝑎 + 0 = 0 + 𝑎 = 𝑎
k.3Existe elemento simétrico: ∀𝑎 ∈ 𝐾 , ∃ 𝑎´ ∈ 𝐾/ 𝑎 + 𝑎´ = 𝑎´ + 𝑎 = 0
k.4 Conmutativa: ∀𝑎, 𝑏 ∈ 𝐾: 𝑎 + 𝑏 = 𝑏 + 𝑎
k.5 Asociativa:∀ 𝑎, 𝑏, 𝑐 ∈ 𝐾: (𝑎 ⋅ 𝑏) ⋅ 𝑐 = 𝑎 ⋅ (𝑏 ⋅ 𝑐)
k.6 Existe elemento neutro: ∃ 𝑒 ∈ 𝐾, ∀𝑎 ∈ 𝐾 / 𝑎 ⋅ 𝑒 = 𝑒 ⋅ 𝑎 = 𝑎
k.7 Existe elemento simétrico: ∀𝑎 ∈ 𝐾 ∗ , ∃𝑎´´ ∈ 𝐾 ∗ / 𝑎. 𝑎´´ = 𝑎´´. 𝑎 = 𝑒
k.8 Distributiva: ∀ 𝑎, 𝑏, 𝑐 ∈ 𝐾: 𝑎(𝑏 + 𝑐) = 𝑎 ⋅ 𝑏 + 𝑎 ⋅ 𝑐
∀ 𝑎, 𝑏, 𝑐 ∈ 𝐾: (𝑎 + 𝑏) ⋅ 𝑐 = 𝑎 ⋅ 𝑐 + 𝑏 ⋅ 𝑐
Ejemplos:
Son cuerpos las siguientes ternas:
53
El conjunto de los números racionales provisto de las leyes de adición y
multiplicación usuales, (ℚ, +, ⋅), es un cuerpo conmutativo con unidad.
Puesto que:
k.1
∀ 𝑎, 𝑏, 𝑐 ∈ ℚ: (𝑎 + 𝑏) + 𝑐 = 𝑎 + (𝑏 + 𝑐)
k.2
∃0 ∈ ℚ ; ∀𝑎 ∈ ℚ/ 𝑎 + 0 = 0 + 𝑎 = 𝑎
k.3
∀𝑎 ∈ ℚ , ∃ 𝑎´ ∈ ℚ/ 𝑎 + 𝑎´ = 𝑎´ + 𝑎 = 0
k.4
∀𝑎, 𝑏 ∈ ℚ, 𝑎 + 𝑏 = 𝑏 + 𝑎
k.5
∀ 𝑎, 𝑏, 𝑐 ∈ ℚ: (𝑎 ⋅ 𝑏) ⋅ 𝑐 = 𝑎 ⋅ (𝑏 ⋅ 𝑐)
k.6
∃1 ∈ ℚ, ∀𝑎 ∈ ℚ / 𝑎 ⋅ 1 = 1 ⋅ 𝑎 = 𝑎
k.7
∀𝑎 ∈ (ℚ − {0}), ∃𝑎−1 ∈ (ℚ − {0}), /𝑎. 𝑎−1 = 𝑎−1 . 𝑎 = 1
k.8
∀ 𝑎, 𝑏, 𝑐 ∈ ℚ: 𝑎(𝑏 + 𝑐) = 𝑎 ⋅ 𝑏 + 𝑎 ⋅ 𝑐
∀ 𝑎, 𝑏, 𝑐 ∈ ℚ: (𝑎 + 𝑏) ⋅ 𝑐 = 𝑎 ⋅ 𝑐 + 𝑏 ⋅ 𝑐
El conjunto de los números reales provisto de las leyes de adición y multiplicación
usuales, (ℝ, +, ⋅), es un cuerpo conmutativo con unidad.
k.1 ∀ 𝑎, 𝑏, 𝑐 ∈ ℝ: (𝑎 + 𝑏) + 𝑐 = 𝑎 + (𝑏 + 𝑐)
k.2 ∃0 ∈ ℝ ; ∀𝑎 ∈ ℝ/ 𝑎 + 0 = 0 + 𝑎 = 𝑎
k.3 ∀𝑎 ∈ ℝ , ∃ 𝑎´ ∈ ℝ/ 𝑎 + 𝑎´ = 𝑎´ + 𝑎 = 0
k.4 ∀𝑎, 𝑏 ∈ ℝ, 𝑎 + 𝑏 = 𝑏 + 𝑎
k.5 ∀ 𝑎, 𝑏, 𝑐 ∈ ℝ: (𝑎 ⋅ 𝑏) ⋅ 𝑐 = 𝑎 ⋅ (𝑏 ⋅ 𝑐)
k.6 ∃1 ∈ ℝ, ∀𝑎 ∈ ℚ / 𝑎 ⋅ 1 = 1 ⋅ 𝑎 = 𝑎
k.7 ∀𝑎 ∈ (ℝ − {0}), ∃𝑎−1 ∈ (ℝ − {0}), /𝑎. 𝑎−1 = 𝑎−1 . 𝑎 = 1
k.8 ∀ 𝑎, 𝑏, 𝑐 ∈ ℝ: 𝑎(𝑏 + 𝑐) = 𝑎 ⋅ 𝑏 + 𝑎 ⋅ 𝑐
∀ 𝑎, 𝑏, 𝑐 ∈ ℝ: (𝑎 + 𝑏) ⋅ 𝑐 = 𝑎 ⋅ 𝑐 + 𝑏 ⋅ 𝑐
54
3.8.1 Propiedades de los cuerpos
Monotonía de la adición respecto a la igualdad.
𝑎 =𝑏 ⟹𝑎+𝑐 =𝑏+𝑐
Monotonía a la derecha.
𝑎 = 𝑏 ⟹ 𝑐+𝑎 = 𝑐+𝑏
Monotonía a la izquierda.
∀𝑎, 𝑏, 𝑐 ∈ 𝐾;
Monotonía de la multiplicación respecto a la igualdad.
𝑎 =𝑏 ⟹𝑎∙𝑐 =𝑏∙𝑐
Monotonía a la derecha.
𝑎 = 𝑏 ⟹ 𝑐∙𝑎 = 𝑐∙𝑏
Monotonía a la izquierda.
∀𝑎, 𝑏, 𝑐 ∈ 𝐾;
Propiedad de la cancelación de la adición respecto a la igualdad.
𝑎+𝑐 =𝑏+𝑐 ⟹𝑎 =𝑏
Cancelación a la derecha.
𝑐+𝑎 = 𝑐+𝑏 ⟹ 𝑎 =𝑏
Cancelación a la izquierda.
∀𝑎, 𝑏, 𝑐 ∈ 𝐾;
Propiedad de la cancelación de la multiplicación respecto a la igualdad.
𝑎∙𝑐 =𝑏∙𝑐 ⟹𝑎 =𝑏
Cancelación a la derecha.
𝑐∙𝑎 = 𝑐∙𝑏 ⟹ 𝑎 =𝑏
Cancelación a la izquierda.
∀𝑎, 𝑏 ∈ 𝐾, ∀ 𝑐 ∈ 𝐾 − {0}:
Propiedad del elemento absorbente.
𝑎 ⋅ 0 = 0 ⋅ 𝑎 = 0; ∀𝑎, 𝑏 ∈ 𝐾
Dado el campo (𝐾, +, ⋅) y 𝑎, 𝑏 ∈ 𝐾; entonces se cumple que:
𝑎⋅𝑏 =0 ⇒𝑎 =0  b=0
3.8.2 Demostración de algunas propiedades:
Propiedad cancelativa de la adición respecto a la igualdad:
a + b = a + c ⟹ (-a)+(a+b) = (-a)+(a+c)
[(-a)+a] + b = [(-a) + a] + c
0+b = 0+c
b = c
Monotonía de la adición
Asociativa de la adición
Opuesto aditivo
Neutro de la adición
55
Nota: La segunda parte se justifica por la ley conmutativa de la adición en el
campo K.
Propiedad cancelativa de la multiplicación respecto a la igualdad.
⟹ (a.c).c-1 = (b.c).c-1
a.c = b.c
Monotonía de la multiplicación
a.(c.c-1) = b.(c.c-1) Asociativa de la multiplicación
a.1 = b.1
a=b
Inverso multiplicativo
Neutro de la multiplicación
Nota: La segunda parte se justifica por la conmutatividad de la multiplicación en el
campo K.
3.8.2.1 Propiedad del elemento absorbente:
a + 0 = a ⟹ a.(a+0) = a.a
a.a + a.0 = a.a+0
a.0 = 0
Monotonía de la multiplicación
Distributiva de la multiplicación respecto a la adición
Cancelación de la adición
Nota: La segunda parte se justifica por la conmutatividad de la multiplicación en el
campo K.
𝑎 ⋅ 𝑏 = 0 ⇒ 𝑎 = 0  b = 0; ∀ 𝑎, 𝑏 ∈ 𝐾.
Es decir, un campo no admite divisores de cero.
Analicemos en términos de a:
- Si a = 0, la disyunción (a = 0  b = 0) es verdadera, y no hay nada que demostrar.
- Si 𝑎 ≠ 0, por definición de campo existe a-1.
Entonces, multiplicando a ambos miembros de la igualdad a. b = 0 por a-1 se tiene:
a-1 . (a.b) = a-1 . 0
(a-1.a).b = 0
1.b = 0
(asociativa de la multiplicación y elemento absorbente).
(inverso multiplicativo)
56
b=0
(neutro de a multiplicación)
El análisis en términos de b es similar.
Por lo tanto, queda demostrado que: 𝑎 ⋅ 𝑏 = 0 ⇒ 𝑎 = 0  b = 0
3.9
Espacio vectorial
Un espacio vectorial consiste en un conjunto de entidades conocidas como
vectores. En este conjunto, se establecen dos operaciones: la adición de vectores y la
multiplicación de un vector por un escalar (un número real o complejo). Además, este
espacio cumple con un conjunto de axiomas.
Ejemplo de espacios vectoriales:
 R^n: Es el conjunto de todas las n-tuplas de números reales. Es un espacio vectorial con
las operaciones de suma y producto por escalar usuales.
 P_n: El conjunto de todos los polinomios de grado n o menos. Este conjunto, con las
operaciones de suma de polinomios y multiplicación de un polinomio por un escalar,
forma un espacio vectorial.
 M_m×n(K): El conjunto de todas las matrices de m filas y n columnas con entradas en
un campo K. Con las operaciones de suma de matrices y multiplicación de una matriz
por un escalar, este conjunto es un espacio vectorial.
 F®: El conjunto de todas las funciones de R en R. Este conjunto, con las operaciones de
suma de funciones y multiplicación de una función por un escalar, es un espacio
vectorial.
Es importante mencionar que cada uno de estos espacios tiene una estructura
algebraica y una representación espacial que resulta muy útil para trabajos en física y
matemáticas
57
 Axiomas para la adición:
Ev1. La adición es una ley de composición interna en 𝕍.
“
+: 𝕍𝑥𝕍 ⟶ 𝕍
O sea: ∀ 𝑥, 𝑦 ∈ 𝕍 ⟹ 𝑥 + 𝑦 ∈ 𝕍
Significa que la suma de dos elementos cualesquiera de 𝕍 es un único elemento de
𝕍.
 Axiomas para el producto por un escalar
Ev2. El producto por un escalar es una ley de composición externa en 𝕍 con
escalares u operadores en 𝕂.
∙: 𝕂𝑥𝕍 ⟶𝕍
Es decir:
Dados 𝛼 ∈ 𝕂
∧ 𝑥 ∈ 𝕍 entonces, 𝛼 ∙ 𝑥 ∈ 𝕍, llamado producto escalar.
O sea:
𝛼∈𝕂 ∧
𝑥∈𝕍
⟹ 𝛼∙𝑥 ∈𝕍
Ejemplos:
 Sea 𝕍 = ℝ y 𝕂 = ℚ, entonces la cuaterna (ℝ, +, ℚ, ⋅) es un espacio vectorial, porque
verifica:
Ev1. Para cada 𝑎 ∈ ℝ, existe (−𝑎) ∈ ℝ que verifica:
𝑎 + (−𝑎) = (−𝑎) + 𝑎 = 0
Ev2. La adición es conmutativa en ℝ.
𝑎 + 𝑏 = 𝑏 + 𝑎; ∀ 𝑎, 𝑏 ∈ ℝ
 Axiomas que cumple el producto por un escalar
Ev3. El producto con escalares en ℚ es una ley de composición externa en ℝ.
O sea, para 𝑘 ∈ ℚ ∧ 𝑎 ∈ ℝ ⟹ 𝑘 ∙ 𝑎 ∈ ℝ
”
Ev4. El producto satisface la asociatividad mixta
58
∀ 𝑘, ℎ ∈ ℚ, ∀ 𝑎 ∈ ℝ: 𝑘 ∙ (ℎ ∙ 𝑥) = (𝑘 ∙ ℎ) ∙ 𝑎
 El Espacio vectorial (ℝ𝟐 , +, ℝ, ⋅ )
Este espacio está conformado por el conjunto ℝ2 cuyos elementos son pares
ordenados de números reales (𝑥1 , 𝑦1 ) representados como:
ℝ2 = {(𝑥, 𝑦) / 𝑥, 𝑦 ∈ ℝ}
Toda operación de adición en ℝ2 y la multiplicación por un escalar va definido a
continuación:
Adición:
+: ℝ2 𝑥 ℝ2 ⟶ ℝ2
((𝑥1 ; 𝑦1 ), (𝑥2 ; 𝑦2 )) ⟶ (𝑥1 + 𝑥2 ; 𝑦1 + 𝑦2 )
Multiplicación por un escalar:
∶ ℝ 𝑥 ℝ2 ⟶ ℝ2
𝛼(𝑥; 𝑦) ⟶ (𝛼𝑥; 𝛼𝑦)
Entonces ℝ2 con toda operación de multiplicación y adición por escalar definidas
hacen de ℝ2 un espacio vectorial.
 (ℝ2 , +), es un grupo abeliano.
En efecto:
59
Ev1. La adición en ℝ2 es una ley de composición interna, en otras palabras la suma
de 2 pares ordenados en números reales es otro ordenado en número real.
Entonces; planteado ambos pares ordenado de número real cual sea (𝑥1 ; 𝑦1 ),
(𝑥2 ; 𝑦2 ) ∈ ℝ2 , se cumple que:
(𝑥1 ; 𝑦1 ) + (𝑥2 ; 𝑦2 ) = (𝑥1 + 𝑥2 ; 𝑦1 + 𝑦2 ) ∈ ℝ2 .
Ev1. La adición en ℝ2 es asociativa.
Sean (𝑥1 ; 𝑦1 ), (𝑥2 ; 𝑦2 ), (𝑥3 ; 𝑦3 ) pares ordenados del conjunto ℝ2 ; entonces:
[(𝑥1 ; 𝑦1 ) + (𝑥2 ; 𝑦2 )] + (𝑥3 ; 𝑦3 ) = (𝑥1 + 𝑥2 ; 𝑦1 + 𝑦2 ) + (𝑥3 ; 𝑦3 )
= ((𝑥1 + 𝑥2 ) + 𝑥3 ; (𝑦1 + 𝑦2 ) + 𝑦3 )
= (𝑥1 + (𝑥2 + 𝑥3 ); (𝑦1 + (𝑦2 + 𝑦3 ))
= (𝑥1 ; 𝑦1 ) + ((𝑥2 + 𝑥3 ; 𝑦2 + 𝑦3 ))
= (𝑥1 ; 𝑦1 ) + [(𝑥2 ; 𝑦2 ) + (𝑥3 ; 𝑦3 )]
Ev2. En ℝ2 existe 𝜃 = (0; 0) llamado vector nulo, tal que:
∀ (𝑥; 𝑦) ∈ ℝ2 : (𝑥; 𝑦) + (0; 0) = (0; 0) + (𝑥; 𝑦) = (𝑥; 𝑦)
En efecto: (𝑥; 𝑦) + (0; 0) = (𝑥 + 0; 𝑦 + 0) = (𝑥; 𝑦)
Ev3. Para todo (𝑥; 𝑦) ∈ ℝ2 , ∃(−𝑥; −𝑦) ∈ ℝ2 tal que:
(𝑥; 𝑦) + (−𝑥; −𝑦) = (−𝑥; −𝑦) + (𝑥; 𝑦) = (0; 0)
Ev4. El producto es distributivo respecto a la suma en ℝ2 .
∀ 𝛼 ∈ ℝ, ∀ (𝑥1 ; 𝑦1 ), (𝑥2 ; 𝑦2 ) ∈ ℝ2 : 𝛼 ∙ (𝑥 + 𝑦) = 𝛼 ∙ 𝑥 + 𝛼 ∙ 𝑦
𝛼 ∙ [(𝑥1 ; 𝑦1 ) + (𝑥2 ; 𝑦2 )] = 𝛼 ∙ (𝑥1 + 𝑥2 ; 𝑦1 + 𝑦2 )
= (𝛼 ∙ (𝑥1 + 𝑥2 ); 𝛼 ∙ (𝑦1 + 𝑦2 ))
= (𝛼𝑥1 + 𝛼𝑥2 ; 𝛼𝑦1 + 𝛼𝑦2 )
60
= (𝛼𝑥1 ; 𝛼𝑦1 ) + (𝛼𝑥2 ; 𝛼𝑦2 )
= 𝛼 ∙ (𝑥1 ; 𝑦1 ) + 𝛼 ∙ (𝑥2 ; 𝑦2 )
 El espacio (ℝ3 , +, ℝ, ⋅ )
Este espacio está constituido por ternas ordenadas de números reales: (𝑥; 𝑦; 𝑧) con
𝑥, 𝑦, 𝑧 ∈ ℝ.
En otras palabras:
ℝ3 = {(𝑥; 𝑦; 𝑧) / 𝑥, 𝑦, 𝑧 ∈ ℝ}
Toda operación en espacio vectorial es definido como:
Adición:
+: ℝ3 𝑥 ℝ3 ⟶ ℝ3
((𝑥1 ; 𝑦1 ; 𝑧1 ), (𝑥2 ; 𝑦2 ; 𝑧2 )) ⟶ (𝑥1 + 𝑥2 ; 𝑦1 + 𝑦2 ; 𝑧1 + 𝑧2 )
Multiplicación por un escalar:
∙ ∶ ℝ 𝑥 ℝ3 ⟶ ℝ3
𝛼(𝑥; 𝑦; 𝑧) ⟶ (𝛼𝑥; 𝛼𝑦; 𝛼𝑧)
En adelante se verificara toda propiedad de ley externa, la ley externa " ∙ " satisface
los siguientes axiomas:
Ev1. El producto por un escalar es una ley de composición externa; es decir:
∙ : ℝ 𝑥 ℝ3 ⟶ ℝ3 ; así dados 𝛼 ∈ ℝ y (𝑥; 𝑦; 𝑧) ∈ ℝ3 entonces:
𝛼 ∙ (𝑥; 𝑦; 𝑧) = (𝛼𝑥; 𝛼𝑦; 𝛼𝑧) ∈ ℝ3
Ev2. Se cumple la asociatividad mixta
∀ 𝛼, 𝛽 ∈ ℝ, ∀ (𝑥; 𝑦; 𝑧) ∈ ℝ3 :
𝛼 ∙ [𝛽 ∙ (𝑥; 𝑦; 𝑧)] = 𝛼 ∙ (𝛽 ∙ 𝑥; 𝛽 ∙ 𝑦; 𝛽 ∙ 𝑧)
= (𝛼𝛽𝑥; 𝛼𝛽𝑦; 𝛼𝛽𝑧)
= (𝛼 ∙ 𝛽) ∙ (𝑥; 𝑦; 𝑧)
Ev3. El producto es distributivo respecto a la suma en ℝ.
∀ 𝛼, 𝛽 ∈ ℝ,
∀ (𝑥; 𝑦; 𝑧) ∈ ℝ3 :
61
(𝛼 + 𝛽) ∙ (𝑥; 𝑦; 𝑧) = 𝛼 ∙ (𝑥; 𝑦; 𝑧) + 𝛽 ∙ (𝑥; 𝑦; 𝑧)
En efecto:
(𝛼 + 𝛽) ∙ (𝑥; 𝑦; 𝑧) = ((𝛼 + 𝛽)𝑥; (𝛼 + 𝛽)𝑦; (𝛼 + 𝛽)𝑧)
= (𝛼 ∙ 𝑥 + 𝛽 ∙ 𝑥; 𝛼 ∙ 𝑦 + 𝛽 ∙ 𝑦; 𝛼 ∙ 𝑧 + 𝛽 ∙ 𝑧)
= (𝛼 ∙ 𝑥; 𝛼 ∙ 𝑦; 𝛼 ∙ 𝑧) + (𝛽 ∙ 𝑥; 𝛽 ∙ 𝑦; 𝛽 ∙ 𝑧)
= 𝛼 ∙ (𝑥; 𝑦; 𝑧) + 𝛽 ∙ (𝑥; 𝑦; 𝑧)
Ev4. El producto es distributivo respecto a la suma en ℝ3 .
∀ 𝛼 ∈ ℝ, ∀ (𝑥1 ; 𝑦1 ; 𝑧1 ), (𝑥2 ; 𝑦2 ; 𝑧2 ) ∈ ℝ3 :
𝛼 ∙ [(𝑥1 ; 𝑦1 ; 𝑧1 ) + (𝑥2 ; 𝑦2 ; 𝑧2 )] = 𝛼 ∙ (𝑥1 ; 𝑦1 ; 𝑧1 ) + 𝛼 ∙ (𝑥2 ; 𝑦2 ; 𝑧2 )
En efecto:
𝛼 ∙ [(𝑥1 ; 𝑦1 ; 𝑧1 ) + (𝑥2 ; 𝑦2 ; 𝑧2 )] = 𝛼 ∙ (𝑥1 + 𝑥2 ; 𝑦1 + 𝑦2 ; 𝑧1 + 𝑧2 )
= (𝛼 ∙ (𝑥1 + 𝑥2 ); 𝛼 ∙ (𝑦1 + 𝑦2 ); 𝛼 ∙ (𝑧1 + 𝑧2 ))
= (𝛼𝑥1 + 𝛼𝑥2 ; 𝛼𝑦1 + 𝛼𝑦2 ; 𝛼𝑧1 + 𝛼𝑧2 )
= (𝛼𝑥1 ; 𝛼𝑦1 ; ; 𝛼𝑧1 ) + (𝛼𝑥2 + 𝛼𝑦2 + 𝛼𝑧2 )
= 𝛼 ∙ (𝑥1 ; 𝑦1 ; 𝑧1 ) + 𝛼 ∙ (𝑥2 ; 𝑦2 ; 𝑧2 )
Ev5. ∀(𝑥; 𝑦; 𝑧) ∈ ℝ3 , existe 1 ∈ ℝ; tal que:
1 ⋅ (𝑥; 𝑦; 𝑧) = (1 ⋅ 𝑥; 1 ⋅ 𝑦; 1 ⋅ 𝑧) = (𝑥; 𝑦; 𝑧)
Ello demuestra que (ℝ3 , +, ℝ, ⋅ ) es un espacio vectorial.
Cada vector (𝑥; 𝑦; 𝑧) en un espacio dado se puede asociar con un vector geométrico
en el espacio tridimensional que comienza en el origen y termina en el punto con
coordenadas (𝑥; 𝑦; 𝑧).
62
Las propiedades geométricas del espacio vectorial (ℝ2 , +, ℝ, ⋅ ) también se
aplican al espacio (ℝ3 , +, ℝ, ⋅ );. En ℝ3 , la suma de vectores sigue la regla del
paralelogramo y la multiplicación por escalares cambia el tamaño del vector, manteniendo
la dirección si r > 0 o invirtiéndola si r < 0.
3.10
Las estructuras algebraicas y las estructuras de la inteligencia
Piaget explora la relación entre las estructuras matemáticas y las estructuras de la
inteligencia. Se pregunta si las conexiones matemáticas son generadas por la inteligencia o
si son descubiertas como una realidad externa.
Identifica tres estructuras matemáticas fundamentales: las estructuras algebraicas
(con el grupo como prototipo), las estructuras de orden y las estructuras topológicas.
Sostiene que las estructuras algebraicas, especialmente los grupos, corresponden a
los mecanismos operatorios de la inteligencia, regidos por la inversión o negación, una de
las dos formas de reversibilidad, también menciona que la noción de grupo refleja
mecanismos clave de la inteligencia, como la coordinación de esquemas de acción, la
reversibilidad de las operaciones, el retorno al punto de partida sin cambios y la
posibilidad de alcanzar el mismo resultado por diferentes caminos.
Las estructuras operatorias de la inteligencia emergen desde el principio con tres
tipos de organización que corresponden a las estructuras algebraicas, de orden y
topológicas en matemáticas. Estas estructuras se coordinan entre sí y generan estructuras
más complejas que son fundamentales para la construcción de conceptos lógicos y
matemáticos.
La enseñanza de las matemáticas debe buscar siempre el rigor lógico y la
comprensión de un formalismo suficiente, y la psicología puede proporcionar datos sobre
cómo lograr esto de manera más segura.
63
Si las matemáticas se basan en estructuras que corresponden a las de la inteligencia,
entonces la didáctica de las matemáticas debe basarse en la organización progresiva de
estas estructuras operatorias. Las operaciones derivan de acciones que se interiorizan y se
coordinan en estructuras.
La experiencia sirve de base para la coordinación de las acciones y la abstracción
“
se refiere a estas acciones y no al objeto. Por lo tanto, la experiencia es la base para la
deducción en lugar de contradecirla. Hay dos tipos de experiencias: la experiencia física,
que conduce a una abstracción de las propiedades del objeto, y la experiencia lógicomatemática, que abstrae a partir de las acciones u operaciones realizadas sobre el objeto.
Por lo tanto, el recurso a la experiencia y a la acción, y en general, la pedagogía
activa, no comprometen el posterior rigor deductivo, sino que lo preparan
proporcionándole bases reales y no simplemente verbales .
”
Figura 1.
Síntesis
64
Figura 2.
Cuadro de estructuras algebraicas
65
Aplicación didáctica
Las operaciones internas y las estructuras algebraicas son la formalización de las
operaciones y sus propiedades con las diferentes clases de números, conjuntos, funciones,
polinomios, vectores, matrices, figuras geométricas y seguramente otros objetos
matemáticos y no matemáticos.
Como afirma Piaget, las estructuras matemáticas son muy importantes en la
abstracción y generalización de ciertas propiedades que pueden tener los conjuntos al
margen de la naturaleza de sus elementos.
Por otra parte, como sostiene el mismo Piaget, dichas estructuras, en especial la
estructura de grupo, tienen una estrecha relación con los mecanismos operatorios de la
inteligencia.
Desde las acciones operatorias concretas (como agrupar, clasificar, ordenar, seriar,
etc.) que realizan los niños en edad preescolar, podemos encontrar analogías con la
asociatividad, conmutatividad, reversibilidad, entre otras propiedades, que sientan las
bases del razonamiento lógico-matemático.
Posteriormente, estas acciones operatorias concretas manipulativas se vuelven
abstractas, formales, hipotético-deductivas, como es el propósito de la enseñanza de la
matemática; puesto que el principio de acción que es fundamental en el proceso de
aprendizaje de la matemática no se refiere únicamente a las acciones concretas de las
etapas iniciales del desarrollo cognitivo, sino que son acciones u operaciones cognitivas
abstractas y generales sobre el objeto matemático; es decir no se queda en la experiencia
física sino que es un proceso que conduce a la abstracción de las propiedades del objeto
mismo.
66
Este es un aspecto fundamental que como docentes debemos rescatar del estudio de
las estructuras algebraicas.
Otro aspecto favorable que nos ofrece el estudio de las estructuras algebraicas, es la
posibilidad de establecer interconexiones o analogías entre diferentes campos temáticos
(como propone Freudenthal), como, por ejemplo, entre los números enteros y los
polinomios, ya que ambos conjuntos provistos de las leyes aditiva y multiplicativa, tienen
la estructura de anillo; y de esa manera promover una mejor comprensión de la
matemática.
Por lo que consideramos importante, sin caer en el extremo que en su momento se
dio, rescatar la identificación y aplicación de las propiedades (clausura, asociativa,
elemento neutro, elemento simétrico, conmutativa, entre otras), no de manera memorística,
sino siguiendo un razonamiento inductivo, como búsqueda de regularidades, promoviendo
que los mismos estudiantes desde la educación básica descubran y formalicen dichas
propiedades.
Consideramos que la resolución de problemas como enfoque del área en el
currículo actual es muy importante; sin embrago es necesario que como docentes los
orientemos a descubrir las diferentes propiedades que además de su utilidad para ir
configurando las estructuras algebraicas, permiten agilizar o simplificar las actividades
operatorias.
De esta manera, el estudio de las operaciones internas y las estructuras algebraicas
no se tendría que dar únicamente en la educación superior, sino que tendría un sustento
muy valioso si se empieza a sentar las bases desde la edad escolar o pre-escolar si fuera
posible.
67
Una enseñanza desde este enfoque contribuiría de manera significativa a que los
estudiantes logren un comprensión de la matemática como u todo unitario y no
fragmentado en partes inconexas e incomprensibles.
Aunque el estudio de las estructuras algebraicas no se mencione explícitamente en
el Currículo Nacional de Educación Básica, se pueden introducir a lo largo de todos los
niveles educativos. Inicialmente, se abordan de manera intuitiva mediante la manipulación
de objetos concretos, luego a través de representaciones gráficas y tabulares, y finalmente
se llega a la formalización simbólica. En secundaria, es crucial que los estudiantes analicen
las estructuras de varios conjuntos numéricos, polinomios, vectores, matrices, etc.
68
Universidad Nacional De Educación
Enrique Guzmán Y Valle
Alma Máter Del Magisterio Nacional
Facultad De Ciencias
Departamento Académico De Matemática E Informática
Plan de Sesión de Aprendizaje
Tema:
Leyes de composición interna y estructuras algebraicas
Presentado Por:
Mario Andrés Auqui Cáceres
Miembros del Jurado:
Presidente
:
Secretario
:
Vocal
:
Chosica, 2019
69
SESION DE APRENDIZAJE
Título de la Sesión: Operaciones internas y estructuras algebraicas
I. Información general
1.1 Área
:
Matemática
1.2 Duración
:
45 min (01 hora pedagógica)
1.3 Docente
:
Mario Andrés Auqui Cáceres
1.4 Lugar
:
Sala de Grados de la Facultad de Ciencias
1.5 Fecha
:
30/12/2019
II. Propósitos y evaluación de los aprendizajes
70
III. Secuencia didáctica
IV. Referencias
71
Guía de Práctica
1. Explique por qué la radicación en el conjunto de números racionales no es una ley de
composición interna.
𝑎.𝑏
2. Pruebe si el conjunto de los números racionales provisto de la operación 𝑎 ∗ 𝑏 = 5
un semigrupo.
3. Verifique si el monoide (ℝ+ , ∗) donde 𝑥 ∗ 𝑦 = 5𝑥𝑦, es un grupo abeliano.
4. Si en un grupo (𝐺, ∗), se tiene que 𝑎2 = 𝑎 ∗ 𝑎 = 𝑒, ∀ 𝑎 ∈ 𝐺.
Demuestre que 𝐺 es abeliano, siendo 𝑒 el neutro de 𝐺.
5. Construyendo la tabla para la multiplicación en ℤ 7, pruebe que (ℤ 7; .) es un grupo.
6. En el conjunto de los números racionales ℚ se definen las operaciones ⊺ y ∗ como
sigue:
𝑎
𝑎 ⊺ 𝑏 = 𝑎 + 𝑏, 𝑏 ≠ 0
𝑥 ∗ 𝑦 = 𝑥 + 𝑦2
Verifique si (ℚ, ⊺,∗ ) es un anillo.
7. Explique por qué el anillo (ℳ2𝑥2 , +, ⋅ ) no es conmutativo.
8. Pruebe si (3ℤ, +, ⋅ ) es un cuerpo.
9. Identifique qué tipo de anillo es (ℤ5 , +, ⋅ ) .
es
72
Síntesis
1. Las operaciones internas y las estructuras algebraicas son conceptos aparentemente
nuevos, sin embargo tienen su base en las diferentes operaciones matemáticas que se
desarrollan desde el nivel primario.
2. El estudio de las operaciones internas y las estructuras algebraicas permite identificar
la estructura que tienen los diferentes conjuntos numéricos con los que interactúa día a
día, por ejemplo es importante tomar conocimiento que el conjunto de los números
naturales con la adición no es un grupo porque no existe el opuesto aditivo, o que la
potenciación en el conjunto de los números enteros no es una LCI, porque si el
exponente es negativo la potencia ya no es un número entero, entre otros.
3. La importancia del estudio de las operaciones internas y las estructuras algebraicas se
basa en su nivel de generalidad en las que caben diferentes tipos de conjuntos y
diferentes operaciones.
4. Según Piaget, las operaciones internas y las estructuras algebraicas tienen relación con
las estructuras cognitivas, por lo que es importante profundizar en su comprensión y
sus implicancias en el proceso de enseñanza-aprendizaje.
5. El estudio de las operaciones internas y las estructuras algebraicas permite al docente
tener una visión más amplia e integrada de la matemática, de manera que pueda
aprovechar esta ventaja para mejorar el nivel de comprensión de los estudiantes,
integrando las diferentes competencias que plantea el actual currículo.
73
Apreciación crítica y sugerencias
El estudio de las operaciones internas y las estructuras algebraicas es muy
importante en la formación de los docentes de la especialidad de matemática, pues permite
tener una nueva mirada de la enseñanza de la matemática, que que va más allá de lo
puramente operatorio, pero no se contrapone a los propósitos que plantea el currículo
actual de la educación básica.
El estudio de las operaciones internas y las estructuras algebraicas permite
profundizar en el estudio de los diferentes campos temáticos estableciendo conexiones
entre ellos, favoreciendo de esta manera el nivel de comprensión de los diferentes
conceptos matemáticos.
Revalorara la importancia de los fundamentos de la matemática va a permitir
completar y afianzar el enfoque que actualmente tiene la enseñanza de la matemática que
como bien sabemos está centrada en la resolución de problemas.
Así como es importante la matemática para resolver problemas, también es
importante desarrollar el razonamiento inductivo e hipotético-deductivo de los estudiantes
a través de la búsqueda de patrones o regularidades como son las diferentes propiedades
que verifican los distintos objetos matemáticos y las estructuras que se van configurando
que además guardan una estrecha relación con las estructuras operatorias de la inteligencia
como plantea Piaget.
 Sugerencias
1. Es necesario incidir en la comprensión e importancia de las operaciones internas y las
estructuras algebraicas en la formación de los estudiantes de educación en la
especialidad de matemática, así como también en los docentes que se encuentran en
ejercicio.
74
2. En el estudio de los sistemas numéricos, funciones, polinomios, matrices, entre otros, es
posible introducir el concepto de estructuras algebraicas en el nivel de educación
secundaria, iniciando con la conceptualización de las operaciones o leyes de
composición interna que generalmente se conoce como la propiedad de clausura.
3. Plantear estrategias creativas y lúdicas en la enseñanza de las estructuras algebraicas a
los estudiantes de educación básica, estableciendo vínculos con situaciones de contexto
en lo posible.
4. Revisar la forma en que se enseñan los polinomios, las matrices y el plano R^2
tanto en secundaria como en niveles superiores, con el objetivo de trascender el
simple cálculo y profundizar en el entendimiento de sus propiedades y
aplicaciones.
5. Revisar el enfoque de la enseñanza de la matemática tanto en la educación secundaria
como en la formación de docentes para que a la vez de la resolución de problemas se
incida en la comprensión conceptual que favorezca el pensamiento hipotéticodeductivo.
75
Referencias
Aizpun, A. (s/f). Teoría y didáctica de la matemática actual. Madrid: Vicens Vives.
Ayres, F. (s/f). Álgebra moderna. México: Mc. Graw-Hill. Colección Schaum.
Bourbaki, N. (1972). Álgebra. Santiago de Chile: Universidad Nacional de Santiago de
Chile.
Carranza, C. (1998). Teoría de conjuntos y números naturales. Lima: Fondo Editorial de la
Pontificia Universidad Católica del Perú.
Carranza, C. (1998). Álgebra. Lima: Fondo Editorial de la Pontificia Universidad Católica
“
del Perú.
Gentile, E. (2002). Estructuras Algebraicas. Monografía N° 03. Washington: OEA. Serie
de Matemática.
Herstein, I. (1979). Álgebra moderna. México: Trillas S. A.
Lang, S. (1971). Álgebra. Madrid: Fondo Educativo Interamericano
Lezama, O. (2014). Cuadernos de álgebra. Bogotá: Universidad Nacional de Colombia.
Lipschutz, S. (1980). Teoría de conjuntos y temas afines. México: Mc. Graw-Hill. Colección
Schaum.
Piaget, J. y otros. (1968). La enseñanza de las matemáticas. Madrid: editorial Aguilar. 3ra.
Ed.
Queysanne, M. (1971). Álgebra básica. Madrid: Vicens Vives.
Rojo, A. (1981). Álgebra I. Buenos Aires : El ateneo.
”