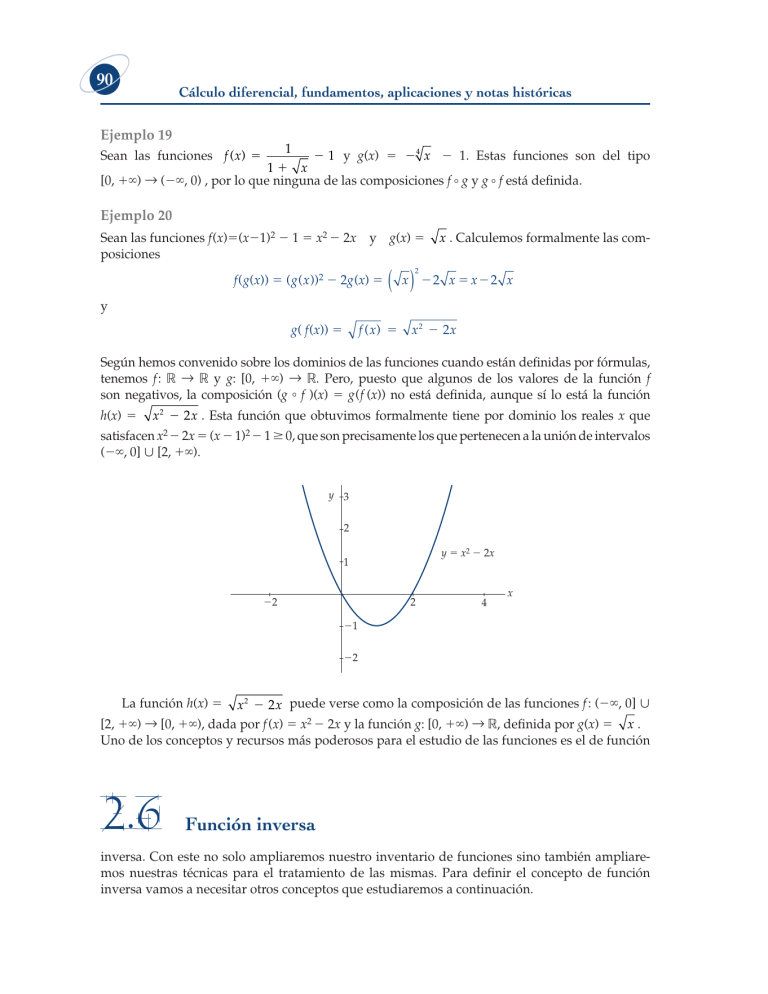
90 Cálculo diferencial, fundamentos, aplicaciones y notas históricas Ejemplo 19 1 1 y g(x) 5 24 x 2 1. Estas funciones son del tipo 11 x [0, 1`) → (2`, 0) , por lo que ninguna de las composiciones f 8 g y g 8 f está deinida. Sean las funciones f ( x) 5 Ejemplo 20 Sean las funciones f(x)5(x21)2 2 1 5 x2 2 2x posiciones y f(g(x)) 5 (g(x))2 2 2g(x) 5 g(x) 5 x . Calculemos formalmente las com- ( x ) 2 x x2 x 2 y f ( x) 5 g( f(x)) 5 x 2 2x Según hemos convenido sobre los dominios de las funciones cuando están deinidas por fórmulas, tenemos f : R → R y g: [0, 1`) → R. Pero, puesto que algunos de los valores de la función f son negativos, la composición (g 8 f )(x) 5 g(f (x)) no está deinida, aunque sí lo está la función h(x) 5 x 2 2 2 x . Esta función que obtuvimos formalmente tiene por dominio los reales x que satisfacen x2 2 2x 5 (x 2 1)2 2 1 $ 0, que son precisamente los que pertenecen a la unión de intervalos (2`, 0] < [2, 1`). y 3 2 y 5 x2 2 2x 1 2 2 4 x 1 2 La función h(x) 5 x 2 2 2 x puede verse como la composición de las funciones f : (2`, 0] < [2, 1`) → [0, 1`), dada por f (x) 5 x2 2 2x y la función g: [0, 1`) → R, deinida por g(x) 5 x . Uno de los conceptos y recursos más poderosos para el estudio de las funciones es el de función 2.6 Función inversa inversa. Con este no solo ampliaremos nuestro inventario de funciones sino también ampliaremos nuestras técnicas para el tratamiento de las mismas. Para deinir el concepto de función inversa vamos a necesitar otros conceptos que estudiaremos a continuación. 91 Funciones 2.6.1 Funciones inyectivas, suprayectivas y biyectivas Consideremos las funciones f : R → R y g: R → R , deinidas como f (x) 5 x2 y g(x) 5 x3 para toda x ∈ R. Hay diferencias cualitativas importantes entre estas dos funciones. Una es que para la función f hay pares de puntos donde toma el mismo valor, por ejemplo f(21) 5 1 y f(1) 5 1. De hecho hay una ininidad de pares de puntos donde f toma el mismo valor f(2a) 5 f(a) 5 a2. En el caso de la función g, esto no ocurre, es decir, siempre que se tomen dos puntos diferentes de su dominio R, digamos a y b, los valores f(a) y f(b) serán diferentes. Una función con esta característica se dice que es inyectiva. La función g es inyectiva, la función f no lo es. Por otra parte, observemos que las dos funciones, f y g, tienen como dominio y contradominio el conjunto R; la función f solo toma valores no negativos, es decir, hay elementos del contradominio que no son valores de la función; por ejemplo, 21 no es un real que pueda ser tomado por la función, es decir, no es un valor de f. Por su parte, la función g toma como valor todo elemento de su contradominio. Una función como g se dice que es suprayectiva. La función f no es suprayectiva. A continuación precisamos estos conceptos. Deinición 3 Sea f : X → Y una función arbitraria. 1. Se dice que f es inyectiva o uno a uno, si puntos diferentes del dominio tienen imágenes diferentes; es decir, si siempre que se tenga x1, x2 ∈ X con x1 x2 se tiene f(x1) f(x2). Una manera equivalente de enunciar esta condición es: si x1, x2 ∈ X son tales que f(x1) 5 f(x2), entonces necesariamente x15 x2. 2. Se dice que f es suprayectiva o sobre, si cada elemento de su contradominio es imagen de al menos un elemento de su dominio. Es decir, si para cada y ∈ Y existe al menos un x ∈ X, tal que y 5 f(x). 3. Se dice que f es biyectiva, si es inyectiva y suprayectiva al mismo tiempo. En forma breve podemos decir que f es suprayectiva si su imagen es todo su contradominio, es decir, si f(X) 5 Y. Por otra parte, que f no sea suprayectiva signiica que existe y ∈Y, para la cual no existe x ∈ X que cumpla y 5 f(x). Dicho de otro modo, f no es suprayectiva si existe y ∈ Y, tal que y f(x) para toda x ∈ X. Una función f : X → Y que no es suprayectiva, “esencialmente puede hacerse” suprayectiva redeiniendo su contradominio, haciéndolo igual a su imagen: f : X → f(X). Sin embargo, en términos estrictos esta función es diferente de la original f : X → Y, pues tiene diferente contradominio, aunque posee lo esencial de ella que es el dominio y la regla de asignación. En términos de las gráicas de funciones reales de variable real podemos interpretar geométricamente inyectividad y la suprayectividad. Que una función f : A → R sea inyectiva signiica que no hay recta horizontal que corte a la gráica en más de un punto; dicho de otra manera, dada cualquier recta horizontal, o bien no corta a la gráica o la corta en un solo punto. Que una función sea no inyectiva signiica que existe al menos una horizontal que corta a la gráica en más de un punto. Que una función 92 Cálculo diferencial, fundamentos, aplicaciones y notas históricas f : A → R sea suprayectiva signiica que sus valores cubren todos los reales; en este caso, toda horizontal cortará a la gráica en al menos un punto. En las siguientes iguras, las líneas punteadas son horizontales que ilustran lo antes descrito. y y x x Inyectiva-No suprayectiva Inyectiva-Suprayectiva y y x x No inyectiva-No suprayectiva No inyectiva-Suprayectiva Ejemplo 21 La función f dada por f(x) 5 x es biyectiva trivialmente. Recordemos que nuestra convención para estos casos es que R siempre será considerado como el contradominio. El dominio dependerá de la fórmula que estemos usando para deinirla. Para la función dada, el dominio también es R. Ejemplo 22 La función f dada por f(x) 5 x3 es inyectiva y también suprayectiva, así que es biyectiva. Probemos que f es inyectiva. Sean a y b reales tales que f(a) 5 f(b); es decir, a3 5 b3. Vamos a probar que esta condición implica a5b. Tenemos entonces a32b350. Pero a3 2 b3 5 (a 2 b)(a2 1 ab 1 b2). 93 Funciones Esto implica que a 2 b 5 0 o bien a2 1 ab 1 b2 5 0. Si se cumple a 2 b 5 0, entonces a 5 b que es lo que deseábamos obtener. Si se cumple a2 1 ab 1 b2 5 0, entonces de la igualdad (que obtenemos completando cuadros). 2 1 3 a ab b a b b 2 2 4 2 2 tenemos que 2 1 3 2 a 2 b 4 b 0 . De aquí obtenemos b 5 0 y a + 21 b = 0 , entonces también a 5 0, por tanto a 5 b. Esto prueba que f es inyectiva. En la siguiente sección analizaremos la suprayectividad. 2.6.2 Una relexión sobre la suprayectividad y teoremas de existencia Que f(x) 5 x3 sea suprayectiva signiica que dado cualquier real a, existe a real, tal que a3 5 a. Esto no es otra cosa que airmar que existe la raíz cúbica de a. Este es un hecho que con seguridad aceptamos sin ningún cuestionamiento, sin embargo, más adelante analizaremos que la existencia de la raíz cúbica de cualquier real o la existencia de la raíz de un orden arbitrario es un caso particular de una problemática más general. Por ejemplo, el problema de averiguar si la función f(x) 5 x3 2 2x 2 1 5x 1 1 es suprayectiva se traduce en el problema de averiguar si la ecuación x3 2 2x2 1 5x 1 1 5 a, que también escribimos x3 2 2x2 1 5x 1 1 2 a 5 0, tiene solución para cualquier real a. Este es un problema similar al de averiguar si la ecuación x3 2 a 5 0 tiene solución, que se reiere a la existencia de las raíces cúbicas para cualquier número real a. En general, el problema de investigar si una función f es suprayectiva, se traduce en el problema de existencia de raíces de la ecuación f(x) 5 a o f(x) 2 a 5 0 . Este problema está estrechamente relacionado con las propiedades de la funciones continuas, las cuales dependen fuertemente de la continuidad de los números reales, que hemos postulado. Como ya lo hemos comentado antes, si una función es inyectiva, pero no suprayectiva, redeiniendo su contradominio, obtenemos una función biyectiva. Hablando en sentido estricto, lo que obtenemos es otra función que, podemos identiicar con la original. En todo caso, podemos ignorar la función original y asignar el mismo nombre a la nueva función obtenida. Así que siempre que tengamos una función inyectiva, puede convenirnos mirarla como una función biyectiva con las modiicaciones mencionadas. Las funciones biyectivas son especialmente importantes, pues establecemos para ellas la siguiente deinición, que es muy importante. Deinición 4 Sea f : X → Y una función biyectiva, su función inversa o simplemente la inversa de f, es la función f 21 : Y → X deinida como sigue: Para cada y ∈ Y, tomamos la única x ∈ X, tal que f(x) 5 y (existe tal x por ser f suprayectiva y es única por ser f inyectiva), entonces hacemos f 21(y) 5 x. 2.6.3 Funciones crecientes y funciones decrecientes Un tipo de función especialmente importante es el de las llamadas funciones crecientes. Estas tienen propiedades asombrosamente interesantes, como veremos en el capítulo 5. Las funciones crecientes, en particular, tienen inversa, lo cual será evidente de su deinición. 94 Cálculo diferencial, fundamentos, aplicaciones y notas históricas Deinición 5 Sea A un subconjunto de los reales y f una función f : A → R. Decimos que f es creciente si siempre que se tengan x, y ∈ A con x , y, se cumple f(x) # f(y). Decimos que f es decreciente si cuando x, y ∈ A con x , y, se cumple f(x) $ f(y). Note que en la deinición anterior el dominio A no necesariamente es un intervalo; puede ser, por ejemplo, la unión de dos intervalos abiertos sin puntos en común. Quizá en este momento sea irrelevante la naturaleza del conjunto, sin embargo en el capítulo 3 volveremos a recordar esta situación. También note que x y y son dos puntos del dominio A que cumplen la desigualdad estricta x , y, sin embargo la desigualdad que deben satisfacer los valores de f en esos puntos es no estricta. Más especíicamente, cuando f es creciente se debe cumplir f(x) # f(y) y cuando f es decreciente, es la desigualdad f(x) $ f(y) la que ha de cumplirse. Cuando se cumplen las desigualdades estrictas para los valores de las funciones, tenemos otras deiniciones. Deinición 6 Sea A un subconjunto de los reales y f una función f : A → R. Decimos que f es estrictamente creciente si siempre que se tengan x, y ∈ A con x , y, se cumple f(x) , f(y). Decimos que f es estrictamente decreciente si cuando x, y ∈ A con x , y, se cumple f(x) . f(y). Complementamos las dos deiniciones anteriores con la siguiente deinición. Deinición 7 Si f : A → R es de cualquiera de los tipos creciente o decreciente, en forma estricta o no estricta, diremos que f es monótona. Si f es estrictamente creciente o estrictamente decreciente diremos que es estrictamente monótona. Un hecho evidente es el siguiente teorema. Teorema Toda función estrictamente monótona es inyectiva, por tanto, tiene inversa. En particular, toda función estrictamente creciente tiene inversa. Ejemplo 23 Mostremos que la función f : R → R, dada por f(x) 5 x3, es estrictamente creciente. En efecto, sean x y y reales cualesquiera tales x , y. Debemos probar que entonces se cumple x3 , y3, para ello factoricemos y3 2 x3. Entonces tenemos y3 2 x3 5 (y 2 x)(x2 1 xy 1 y2). Como y . x, tenemos que el factor y 2 x es positivo. Mostremos que el otro factor x2 1 xy 1 y2 también es positivo, independientemente de los signos de x y y. El factor x2 1 xy 1 y2 se puede escribir 2 x 2 xy y 2 x 2 xy 1 2 3 1 3 y y 2 x y y 2 4 4 2 4 95 Funciones así que x2 1 xy 1 y2 $ 0. Observe que el miembro derecho de la expresión de arriba toma el valor cero solo cuando y 5 0 y, por tanto, solo cuando x 5 y 5 0. Pero, por hipótesis x , y, así que bajo esta condición siempre se tiene x2 1 xy 1 y2 . 0. Esto prueba que cada factor del miembro derecho de la expresión y3 2 x3 5 (y 2 x)(x2 1 xy 1 y2) es positivo, por lo cual al inal obtenemos x3 , y3. Esto prueba que f es estrictamente creciente. Ejemplo 24 Dado que la función f : R → R, dada por f(x) 5 x3, es estrictamente creciente, tiene inversa f 21 : R → R. La función inversa es precisamente la función raíz cúbica f 21(x) 5 3 x . Las gráicas de ambas funciones se ilustran a continuación. y 3 y 2 y 3 x 2 1 1 y 5 x3 2 2 4 x 2 2 1 1 2 2 f 1 ( x) 3 x f(x) 5 x3 Ejemplo 25 Sea la función f : R → R, dada por x si 2` , x # 0 f(x) 5 x 1 1 si 0 , x , 1 x 1 2 si 1 # x , 2` Esta función es estrictamente creciente; su función inversa es: x si 2` , x # 0 f 21(x) 5 x 2 1 si 1 , x , 2 x 2 2 si 3 # x , 1` En las siguientes iguras se ilustran la gráicas de ambas funciones f y f 21. x 96 Cálculo diferencial, fundamentos, aplicaciones y notas históricas y 5 y 5 4 4 3 3 2 2 1 1 2 2 4 x 2 2 1 1 2 2 3 3 4 x Observe que el dominio de la función f, es el intervalo R, mientras que el dominio de f 21 consiste de la unión de intervalos ajenos, a saber (2`, 0] < (1, 2) < [3, 1`). Retomaremos esta función en el capítulo 5, con el in de ilustrar un asombroso teorema. 2.6.4 Una caracterización de la función inversa Dada una función f : X → Y biyectiva, observemos que su función inversa f 21 : Y → X satisface por deinición las siguientes relaciones f 21( f(x)) 5 x para toda x ∈ X f( f 21(y)) 5 y para toda y y ∈ Y. Invitamos al lector a que justiique con cuidado cada una de las relaciones. De hecho, estas condiciones determinan la función inversa; es decir, si f : X → Y es cualquier función para la cual conocemos g : Y → X, que satisface las relaciones g 8 f 5 IX (identidad X → X) y f 8 g 5 IY (identidad Y → Y) podemos estar seguros que g es la función inversa f 21. Este es un teorema que formularemos y probaremos más adelante en esta sección. Mientras tanto, es importante advertir que deben cumplirse ambas relaciones, si solo se satisface una de ellas, entonces no necesariamente signiica que una es la inversa de la otra. Ejemplo 26 Sea f : R → [0, 1`) dada por f (x) 5 x2 y g : [0, 1`) R, deinida como g(x) 5 Entonces tenemos x. 97 Funciones ( f g )( x ) 5 f ( g( x )) 5 ( x) 2 5 x. Así que f 8 g : [0, 1`) → [0, 1`), es la función identidad I[0, 1`), sin embargo, f no es la función inversa de g, pues ( g 8 f )(x) 5 x2 5 u x u. Cuando solo se cumple una de las igualdades g 8 f 5 IX o f 8 g 5 IY, es posible airmar lo siguiente. Proposición Sean f : X → Y y g : Y → X dos funciones cualesquiera, tales que f 8 g : Y → Y es la función identidad Iy : Y → Y, es decir, ( f 8 g)(y) 5 y para toda y ∈ Y, entonces g es inyectiva y f es suprayectiva. Demostración Mostremos que g inyectiva: Sean y1 y y2 elementos de Y, tales que g(y1) 5 g(y2). Se tiene entonces f(g(y1)) 5 f(g(y2)). Pero ( f 8 g)(y) 5 f(g(y)) 5 y para toda y ∈ Y, por tanto, f(g(y1)) 5 y1 y f(g(y2)) 5 y2, lo cual implica y1 5 y2. Esto prueba que g es inyectiva. Mostremos que f es suprayectiva: Elijamos un punto arbitrario y del contradominio Y de f. Como y está en el dominio de g, sea x 5 g(y). Se tiene entonces f (x) 5 f(g(y)) 5 ( f 8 g)(y) 5y Esto prueba que es f suprayectiva. Como consecuencia inmediata de esta proposición tenemos. Proposición Si dos funciones, f : X → Y y g : Y → X satisfacen las condiciones y g 8 f 5 IX f 8 g 5 IY , donde IX : X → X e IY : Y → Y son las funciones identidad en X y Y, respectivamente, entonces ambas funciones, f y g, son biyectivas. De lo anterior se sigue de manera inmediata el teorema prometido. 98 Cálculo diferencial, fundamentos, aplicaciones y notas históricas Teorema Sea f : X → Y una función tal que existe otra función g : Y → X que satisface las relaciones g 8 f 5 IX y f 8 g 5 IY . Entonces f es biyectiva y g es la función inversa f 21. La siguiente proposición es un resultado evidente. Proposición Si f : X → Y es una función biyectiva, entonces así lo es f 21 : Y → X, además ( f 21)21 5 f. La siguiente proposición también se prueba con facilidad. Proposición Sean f : X → Y y g : Y → Z funciones biyectivas, entonces la composición g 8 f : X → Z es biyectiva. Demostración Mostremos que g 8 f es inyectiva: Sean x1 y x2 elementos diferentes de X. Como f es inyectiva, tenemos que f(x1) f(x2). Por otra parte, como g es inyectiva, tenemos que g( f(x1)) g( f(x2)), es decir (g 8 f )(x1) (g 8 f )(x2). Esto prueba que g 8 f es inyectiva. Mostremos que g 8 f es suprayectiva: Sea z ∈ Z. Como g es suprayectiva, podemos tomar y ∈ Y, tal que g(y) 5 z. Como f es suprayectiva, para la y anterior existe x ∈ X, tal que f (x) 5 y. Para esta x se tiene, entonces, g( f(x)) 5 z, es decir, ( g 8 f )(x) 5 z. Esto prueba que g 8 f es suprayectiva. Hemos probado que g 8 f es biyectiva. De esta proposición concluimos que si dos funciones, f y g, tienen inversas y está deinida su composición g 8 f, entonces esta composición tiene inversa. Esto es lo que se establece en el siguiente teorema. Teorema Sean f : X → Y y g : Y → Z funciones biyectivas. Entonces, la composición g 8 f : X → Z tiene inversa ( g 8 f )21: Z → X y está dada por (g 8 f )21 5 f 21 8 g21. Es decir (g 8 f )21(z) 5 f 21(g21(z)) para toda z ∈ Z. La gráica de la función inversa se relaciona de manera muy interesante con la gráica de la función original; ese será nuestro siguiente tema. 2.6.5 Gráica de la función inversa En el ejemplo 23 mostramos las gráicas de las funciones f (x) 5 x3 y g(x) 5 3 x , las cuales son mutuamente inversas 99 Funciones y 3 y 3 2 2 1 1 2 2 x 4 2 2 1 1 2 2 4 x Graiquemos ambas funciones en un mismo sistema de referencia. y 1.5 1 0.5 2 1 1 2 x 0.5 1 1.5 Observemos la simetría que guardan ambas gráicas respecto de la recta h(x) 5 x. La razón de esto es muy simple: si un punto (x, y) pertenece a la gráica de una función f : X → Y, entonces el punto (y, x) pertenece a la gráica de su inversa g : Y → X: y (y, x) (x, y) x