Elementos básicos de Aritmética

Algunos elementos básicos de Aritmética
Marco teórico:
1. Divisibilidad
Se dice que un número es divisible entre otro cuando éste lo contiene exactamente un número
entero de veces. O sea, si dividimos un número entre otro número, el cuociente debe ser
un número entero y su residuo debe ser cero.
Ejemplo: 100 es divisible por 4, porque su cuociente es 25 y el residuo es cero
•
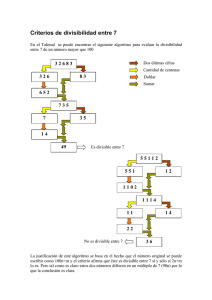
Criterios de divisibilidad
Son ciertas señales matemáticas que nos permiten descubrir por simple observación, si un
número es divisible por otro.
•
Divisibilidad por 2
Un número es divisible por 2 cuando termina en cero o una cifra par.
•
Divisibilidad por 3
Un número es divisible por 3 cuando la suma de los valores absolutos de sus cifras es un
múltiplo de 3.
•
Divisibilidad por 4
Un número es divisible por cuatro cuando sus dos últimas cifras de la derecha forman un
múltiplo de 4 o son ceros.
•
Divisibilidad por 5
Un número es divisible por 5 cuando termina en cero o 5.
•
Divisibilidad por 6
Un número es divisible por 6 cuando es divisible por 2 y 3 al mismo tiempo.
•
Divisibilidad por 8
Un número es divisible por 8 cuando sus tres últimas cifras de la derecha forman un
múltiplo de 8 o son ceros.
•
Divisibilidad por 9
Un número es divisible por 9 cuando la suma de los valores absolutos de sus cifras es
múltiplo de 9.
•
Divisibilidad por 10
Un número es divisible por 10 si su última cifra de la derecha es cero.
2. Definición de naturales, cardinales y enteros
•
Números Naturales: (IN) Son los números de la forma IN = {1,2,3,4,5...}
•
Números Cardinales: (IN0) Son los números de la forma IN0 = {0,1,2,3,4,5,...}
•
Números Enteros: (Z) Son los números de la forma Z = {... -4,-3,-2,-1,0,1,2,3,4,...}
3. Prioridad de operatoria matemática
1)
2)
3)
4)
Paréntesis
Potencias y Raíces
Multiplicación y división (de izquierda a derecha)
Adición y sustracción
4. Sucesor y antecesor en los números enteros
Un sucesor se obtiene sumando 1 a un número o expresión. Ejemplo: el sucesor de n es (n+1)
(con n perteneciente a Z).
Un antecesor se obtiene restando 1 a un número o expresión. Ejemplo: el antecesor de n es
(n - 1) (con n perteneciente a Z).
5. Enunciados frecuentes
Como una parte importante de la resolución de un ejercicio matemático consiste en entender
completamente el enunciado de una pregunta, revisaremos algunas frases muy utilizadas.
Siendo x e y números enteros:
1
x
2
•
El doble de x:
2x
•
la mitad de x o un medio de x:
•
El triple de x:
3x
•
•
El cuádruple de x:
4x
•
•
El quíntuple de x:
5x
•
1
x
3
1
la cuarta parte de x o un cuarto de x:
x
4
1
la quinta parte de x o un quinto de x:
x
5
•
La semisuma de x e y :
(x + y)
2
la tercera parte de x o un tercio de x:
Actividades
a)
Verdadero o falso:
i)
ii)
iii)
iv)
b)
IN IN0
IN Z
Z IN
Z IN0
Complete el término faltante en las siguientes secuencias
i)
ii)
iii)
iv)
1,2,3,4, _ ,6,...
2,4, _ ,8,10,...
1,-2,3,-4, _ ,-6,7,...
1,1,2,3,5,8, _ ,21,...
c)
Siendo “n” un entero, señale cuáles son los dos sucesores consecutivos a n
d)
Siendo “n” un entero, señale cuáles son los dos antecesores consecutivos a n
e)
Siendo “2n” un entero par, señale cuáles son los dos sucesores pares consecutivos de
2n
Ejercicios PSU.
1.
Al sumar el quinto y el sexto término de la secuencia:
x - 6, 2x + 5, 3x - 4, 4x + 3, 5x - 2 ,. . . , resulta:
A)
B)
C)
D)
E)
2.
Si al entero (-2) le restamos el entero (-5), resulta:
A)
B)
C)
D)
E)
3.
11x - 1
11x +1
-x - 1
6x + 1
6x –1
-7
-3
1
3
7
El triple de (2(4 + 3) -2(1 -2)) =
A)
B)
C)
D)
E)
3
7
16
48
64
4.
La expresión 4(1 + 8) es divisible por:
I) 2
A)
B)
C)
D)
E)
5.
Sólo I
Sólo II
Sólo III
Sólo I y II
I, II y III
-15
-10
-8
8
15
La quinta parte del doble de la décima parte de cinco veces 50, resulta:
A)
B)
C)
D)
E)
7.
III) 6
-(4 - 2(3 - 5)) =
A)
B)
C)
D)
E)
6.
II) 3
2
10
15
20
50
La quinta parte de veinticinco veces veinticinco, resulta:
A)
B)
C)
D)
E)
5
25
50
125
225
8.
Si un número es divisible por 10 y 2, siempre es verdadero asegurar que además es
divisible por:
I)
A)
B)
C)
D)
E)
9.
III)
6
Sólo I
Sólo II
Sólo III
Sólo I y II
I, II y III
La edad de Francisco equivale al doble de la quinta parte de la semisuma de (4 +6). ¿Qué
edad tiene Francisco?
A)
B)
C)
D)
E)
10.
II) 5
3
1
2
3
5
10
Si 14 veces 2 es igual a X ,y 15 veces 3 es igual a W, entonces X + W resulta:
A)
B)
C)
D)
E)
14
15
28
45
73