Modelos de Flujo Máximo y Mínimo: Algoritmo Ford-Fulkerson
Anuncio

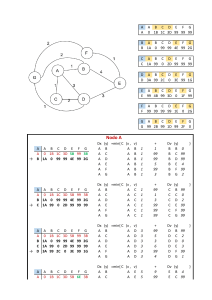
MODELOS DINAMICOS DE INVESTIGACIÓN DE OPERACIONES Tema: Modelos de redes. Subtema: Modelo de flujo máximo o flujo mínimo. Alumno: José Luis Bernal Alonso. Grupo: ING8DL Matricula: 63224881 Carrera: Licenciatura en Ingeniería Industrial. Escuela: Universidad Interglobal Querétaro. Docente: Rogelio Paulin Monroy. Fecha: Noviembre 2024. Contenido Introducción ____________________________________________________________2 Definiciones básicas. ____________________________________________________3 Flujo. ________________________________________________________________3 Capacidad de flujo. ____________________________________________________3 Origen del flujo. _______________________________________________________3 Destino de flujo. _______________________________________________________4 Capacidades residuales. ________________________________________________4 Algoritmo de Ford-Fulkerson. _____________________________________________4 Desarrollo (Solución) ____________________________________________________6 Flujo máximo de la red ________________________________________________ 11 Conclusión ____________________________________________________________ 11 Introducción El modelo de flujo máximo y flujo mínimo se utilizan en teoría de redes para optimizar el movimiento de recursos a través de una red, como un sistema de carreteras, tuberías o cables de transmisión. El modelo de flujo máximo se enfoca en maximizar el flujo total que se puede enviar desde un nodo de origen a un nodo de destino sin exceder las capacidades de las conexiones intermedias. Este modelo es relevante en aplicaciones como la planificación de transporte y la gestión de redes eléctricas. Por otro lado, el modelo de flujo mínimo se utiliza para minimizar el costo o esfuerzo necesario para satisfacer una cierta demanda, como reducir los costos en redes de distribución o minimizar el desperdicio en cadenas de suministro. Ambos modelos son fundamentales en la optimización de redes y encuentran aplicaciones en ingeniería, logística y ciencias de la computación. Definiciones básicas. Flujo. Flujo en vivo o circulación de unidades homogéneas llevando un producto o sustancia que atraviesa una superficie en una medida de tiempo. Capacidad de flujo. Es la cantidad máxima de flujo que puede ingresar a través del nodo fuente y salir por el nodo de destino. Origen del flujo. Es el principal nodo por el cual el flujo ingresa. Destino de flujo. Es el nodo final por el cual el flujo sale. Capacidades residuales. Son aquellas capacidades restantes del arco una vez pasado algún flujo por él. Algoritmo de Ford-Fulkerson. a) El flujo siempre es positivo y de unidades enteras. b) El flujo a través de un arco es menor o igual que la capacidad. c) El flujo que entra en un nodo es igual al que sale de él. Este algoritmo propone caminos y que se pueda aumentar el flujo hasta que se alcance el flujo máximo, encontrando la ruta de penetración con un flujo positivo neto que una los nodos de origen y destinó. El nodo 1 (N1) contiene 3 arcos que conectan con los nodos: 2,3 y 4. Cada arco tiene un número que representa el valor máximo que puede enviar desde el nodo origen (N1) a través de los nodos intermediarios para llegar al nodo destino (N5). i. El nodo origen (N1 para este caso), se coloca la siguiente etiqueta [∞, -]. ii. iii. iv. v. En el nodo origen encontramos los valores 10, 30 y 20, se debe elegir el arco que tenga mayor flujo siendo este el 30 que hace conexión con el N3. En el N3 se coloca la siguiente etiqueta [30,1]. En el nodo 3 (N3) encontramos los valores 0, 0, 10 y 20 igual que en el paso anterior elegimos el arco con mayor flujo siendo este el 20 que hace conexión con el N5. En el N5 se coloca la siguiente etiqueta [20,3]. Los pasos descritos anteriormente los podemos ver gráficamente de la siguiente manera: 0 El nodo de origen (N1), siempre se etiqueta con - 20 El nodo 5 (N5) se etiqueta con [20,5] en donde 20 indica el valor y el 5 indica de que nodo proviene. 5 0 10 1 - 4 30 5 0 [20,5] 0 20 0 2 10 0 30 40 0 3 20 [30,1] El nodo 3 (N3) se etiqueta con [30,1] en donde 30 indica el valor y el 1 indica de que nodo proviene. Con la ruta definida podemos empezar a restar el flujo de traspaso a las capacidades de cada arco y para ello utilizaremos la siguiente formula: Cij,ji(Ci-k,Cj+k) C representa capacidad de flujo. i, j son los índices de los nodos emisor y receptor k es el menor flujo que se traspaso del nodo origen al de destino Para conocer el valor de “k” identificamos la capacidad de flujo de cada uno de los nodos involucrados en nuestra ruta k = min ( C N1,C N2, C N3) y de ese grupo de valores seleccionamos y usamos el menor de ellos y por lo tanto es el que asigna el valor de k: 0 4 20 5 0 10 1 - 0 30 5 0 [20,5] 20 10 30 k = min ( El valor mínimo del conjunto es 20, por lo cual: 2 0 k = 20 0 40 3 0 20 [30,1] Desarrollo (Solución) Iniciemos entonces a realizar las iteraciones que sean necesarias hasta para conocer cual es el flujo máximo de la red. Recordemos nuestra formula: Cij,ji(Ci-k,Cj+k) En donde vamos a sustituir los valores correspondientes a la red que tenemos: 1ra Iteración 0 4 20 5 0 10 - 1 0 30 5 0 20 10 30 0 2 [20,5] 0 40 0 3 20 [30,1] k = min (∞, 30, 20) → k= (20) Cij,ji(Ci-k,Cj+k) C13 indica desde donde se paso el flujo (del N1 al N3) y 31 seria desde el N3 al N1; por lo que a “13” se le resta el valor de k y a “31” se le debe sumar el valor de k, lo mismo pasa para C35,53: C13,31(30-20,0+20)= (10,20) C35,53(20-20,0+20)= (0,20) Los resultados obtenidos serán quienes reemplacen los datos originales de capacidad de flujo a función de actualizar nuestra red, permitiendo que continuemos avanzar en nuestra actividad, quedando de la siguiente forma: 0 20 4 5 0 10 - 0 10 1 5 20 20 30 2 0 10 20 40 0 3 0 2da. Iteración Para la 2da iteración determinamos en el nodo origen el arco que actualmente tiene la mayor capacidad de flujo indicando la dirección al siguiente nodo donde tambien identificaremos el arco con mayor capacidad de flujo y avanzar los nodos necesarios para llegar al nodo destino: [10,3] 0 4 5 10 - 20 0 0 10 1 5 [20,5] 20 20 30 0 2 [20,1] 20 40 0 10 3 0 [40,2] Hemos trazado nuestra nueva ruta de acuerdo a los arcos con mayor capacidad de flujo y se han colocado las etiquetas para cada nodo involucrado, usando nuestras formulas y reemplazando los datos correspondientes se desarrollan los siguientes datos: k = min (∞, 20, 40, 10, 20) → k= (10) Cij,ji(Ci-k,Cj+k) [10,3] 0 1 Cij,ji (Ci-k, Cj+k) k = 10 4 5 10 - 20 0 0 10 5 [20,5] 2 0 20 30 2 0 [20,1] 40 20 0 10 3 0 [40,2] Los resultados obtenidos sustituyen a los anteriores según el nodo correspondiente y con esta actualización obtenemos el nuevo diagrama de la ruta con las capacidades de flujo ajustadas. 0 15 10 - 1 10 4 10 0 10 5 20 10 30 10 2 20 30 10 0 3 0 Antes de continuar observemos que las capacidades del flujo del nodo de origen son igual por lo que podríamos escoger cualquiera de los 3 arcos disponibles (N1-N2, N1-N3 o N1-N4), a fin de hacer mas eficiente nuestro proceso tenemos disponible el arco formado por el nodo 2 y el nodo de destino (N2N5). 3ra Iteración 10 0 4 10 - 1 k= min k= 10 10 15 5 0 10 20 10 0 30 2 10 [30,2] 20 30 10 3 0 [10,1] 10 0 4 1 - 10 15 10 Con los datos obtenidos realizamos las sustituciones correspondientes quedando la red actualizada como lo muestra la figura de lado derecho 5 10 10 20 0 0 20 2 20 20 30 3 10 0 4ta. Iteración 10 0 4 10 15 10 k= min k= 10 1 - 10 10 5 20 [20,2] 0 0 20 20 2 [10,3] 20 30 10 3 0 [10,1] Una vez calculados las nuevas capacidades de los arcos que forman nuestra ruta se sustituyen en el grafico para actualizar nuestra red de nodos y continuar trabajando como se muestra en la siguiente imagen 10 0 TABLA CON LA NUEVAS CAPACIDADES QUE DEBEN TENER LOS ARCOS DE NUESTRA RED 4 10 15 10 5 20 0 1 - 20 0 0 10 2 20 30 40 3 0 0 5ta. Iteración En esta parte nos encontramos que el nodo origen (N1) solo nos queda un camino a elegir solo uno de los arcos conectados al N1 cuenta con capacidad de flujo y la ruta queda trazada como lo vemos en la imagen que está a continuación. k= min k= 10 [10,1] 0 10 15 10 0 1 - 10 4 5 20 20 0 0 10 Una vez obtenidas las nuevas capacidades residuales, repetimos los mismos pasos de las iteraciones pasadas para la sustitución de los valores anteriores con los nuevos, viendo el progreso de nuestra red y saber si debemos continuar o hemos terminado 2 20 [10,4] 30 40 3 0 0 La red de nodos actualizada muestra que todos los arcos del nodo origen tienen valor por lo cual la iteraciones no pueden continuar, 10 0 20 15 0 20 0 1 - 4 5 20 0 10 20 2 30 40 0 0 3 0 Flujo máximo de la red El flujo máximo de la red se obtiene con la sumatoria de los valores de “k” que obtuvimos en cada una de las iteraciones realizadas en el ejercicio: K1 + K2 + K3 + K4 + K5 Donde: K1 = 20, K2 = 10, K3 = 10, K4 = 10 y K5 = 10, Entonces: K1 + K2 + K3 + K4 + K5 = 20+10+10+10+10 = 60 Por lo cual podemos declarar que el flujo máximo de la red equivale a 60 unidades como máximo que podemos mover desde el nodo de origen (N1) hasta el nodo de destino (N5) a través de nuestra red de nodos disponibles de acuerdo al ejercicio anterior. Conclusión El algoritmo Ford-Fulkerson se basa en buscar caminos con mayor flujo desde un origen, hasta el destino aumentando el flujo en esos caminos hasta que ya no se pueda hacer más. Comienza eligiendo el arco de mayor valor en el origen. para que se busque un camino desde el nodo origen hasta el nodo final por donde se pueda aumentar el flujo. Cuando ya no se pueda encontrar un nuevo camino con capacidad residual, el algoritmo termina Este modelo permite a quien lo implementa, maximizar la distribución de materiales dentro de las limitaciones físicas de la red y garantizar que se optimice el uso de los recursos disponibles.