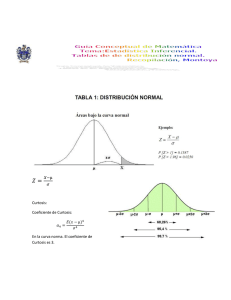
Indice Curtosis .......................................................................................................................... 2 Definición.................................................................................................................... 3 Fórmulas y ecuaciones ................................................................................... 3 — Curtosis de acuerdo a la presentación de los datos 3 K=g2-3 ........................................................................................................................ 4 Los salarios de 3 departamentos ....................................................... 4 Los resultados de un examen ............................................................... 5 Ejemplo resuelto de curtosis .................................................................... 6 K = g2-3 1.675-3 = -1.325 ...................................................................... 7 Curtosis La curtosis o kurtosis es un parámetro estadístico que sirve para caracterizar la distribución de probabilidad de una variable aleatoria, indicando el grado de concentración de los valores alrededor de la medida central. Esto también se conoce como "grado de pico" El término proviene del griego "kurtos" que significa arqueado, por lo tanto la curtosis señala el grado de apuntamiento o achatamiento de la distribución, como se ve en la siguiente figura: figura l. Diferentes tipos de curtosis. Fuente: F. Zapata. Casi todos los valores de una variable aleatoria tienden a agruparse alrededor de un valor central como la media. Pero en algunas distribuciones, los valores están más dispersos que en otras, dando como resultado curvas más aplanadas o más esbeltas. Índice del artículo [Mostrarl Definición La curtosis es un valor numérico propio de cada distribución de frecuencias, que de acuerdo a la concentración de los valores alrededor de la media, se clasifican en tres grupos: —Leptocúrtica: en la cual los valores están muy agrupados alrededor de la media, por lo que la distribución se presenta bastante apuntada y esbelta, (figura l, izquierda). — Mesocúrtica: posee una concentración moderada de valores alrededor de la media (figura I en el centro). —Platicúrtica: está distribución tiene una forma más ancha, pues los valores tienden a estar más dispersos (figura I a la derecha). Fórmulas y ecuaciones La curtosis puede tener cualquier valor, sin limitaciones. Su cálculo se lleva a cabo dependiendo de la manera en que se entreguen los datos. La notación empleada en cada caso es la siguiente: -Coeficiente de curtosis: ge -Media aritmética: X o x con barra -Un valor i-ésimo: Xi -la desviación estándar: a -El número de datos: N -la frecuencia del valor i-ésimo:fi -Marca de clase: mxi Con esta notación, presentamos algunas de las fórmulas más utilizadas para encontrar la curtosis: — Curtosis de acuerdo a la presentación de los datos Datos sin agrupar o agrupados en frecuencias Datos agrupados en intervalos Exceso de curtosis También llamado coeficiente de apuntamiento de Fisher o medida de Fisher, sirve para comparar la distribución en estudio con la distribución normal. Cuando el exceso de curtosis vale 0, estamos en presencia de una distribución normal o campana de Gauss. De esta forma, siempre que se calcule el exceso curtosis de una distribución, en realidad la estamos comparando con la distribución normal. Tanto para los datos sin agrupar como para los datos agrupados, el coeficiente de apuntamiento de Fisher, denotado por K, es: K=g2-3 Ahora bien, se puede demostrar que la curtosis de la distribución normal es 3, por tanto lo si el coeficiente de apuntamiento de Fisher es 0 0 cercano a 0 y se distribución tiene una mesocúrtica. Si K >0 la distribución es leptocúrtica y si K<O es platicúrtica. ;.Para qué sirve la curtosis? La curtosis es una medida de variabilidad utilizada para caracterizar la morfología de una distribución. De esta forma se pueden comparar distribuciones simétricas con el mismo promedio e igual dispersión (dada por la desviación estándar). Disponer de medidas de variabilidad asegura que los promedios sean confiables y ayuda a controlar las variaciones de la distribución. A modo de ejemplo, analicemos estas dos situaciones. Los salarios de 3 departamentos Supongamos que el siguiente gráfico muestra las distribuciones en el salario de 3 departamentos de una misma compañía: figura 2. Tres distribuciones con curtosis distintas ilustran situaciones prácticas. (Elaborado por Fanny Zapata) La curva A es la más esbelta de todas, y de su forma se infiere que la mayor parte de los salarios de ese departamento está muy cercano a la media, por lo tanto la mayoría de los empleados reciben compensaciones parecidas. Por su parte en el departamento B, la curva de los salarios sigue una distribución normal, ya que la curva es mesocúrtica, en la que suponemos que los salarios quedaron distribuidos al azar. Y finalmente tenemos la curva C que es muy achatada, una señal de que en este departamento el rango salarial es mucho más amplio que en los otros. Los resultados de un examen Supongamos ahora que las tres curvas de la figura 2 representan los resultados de un examen aplicado a tres grupos de alumnos de una misma asignatura. El grupo cuyas calificaciones se representa por la curva A leptocúrtica, es bastante homogéneo, la mayoría obtuvo una calificación promedio o cercana. También es posible que el resultado se debiera a que las preguntas del examen tenían más o menos el mismo grado de dificultad. En cambio los resultados del grupo C indican una mayor heterogeneidad en el grupo, que probablemente contiene estudiantes promedio, algunos alumnos más aventajados y seguramente otro tanto menos atentos. O pudo significar que las preguntas de la prueba tenían muy distintos grados de dificultad. La curva B es mesocúrtica, indicativa de que los resultados de la prueba siguieron una distribución normal. Este suele ser el caso más frecuente. Ejemplo resuelto de curtosis Hallar el coeficiente de apuntamiento de Fisher para las siguientes calificaciones, obtenidas en un examen de Física a un grupo de alumnos, con una escala del I al IO: 5, 5, 4, 7, 7,7, 9, 8, 9, 4, 3 Solución Se utilizará la siguiente expresión para datos no agrupados, dada en las secciones precedentes: 92 ¯Ñ K = g2-3 Este valor permite conocer el tipo de distribución. Para calcular g2 es conveniente hacerlo de manera ordenada, paso a paso, ya que hay que resolver varias operaciones aritméticas. Paso 1 En primer lugar se calcula el promedio de las calificaciones. Hay N — ll datos. (5+5+4+7+7+7+9+8+9+4+3)/ 11 cual se utiliza esta ecuación: o = 1.992 O también se puede construir una tabla, que igualmente se requiere para el siguiente paso y en la que se escribe cada término de las sumatorias que se van a necesitar, comenzando por (XI — X), luego (Xi — y luego (Xi — . Paso 3 Efectuar la sumatoria indicada en el numerador de la fórmula para g2. Para esto se utiliza el resultado de la columna derecha de la tabla anterior: (Xi 290.15 Por lo tanto: g2 (1/11) x 290.15 /1.9924 1.675 El coeficiente de apuntamiento de Fisher es: K = g2-3 1.675-3 = -1.325 Lo que interesa es el signo del resultado, que al ser negativo corresponde a una distribución platicúrtica, lo cual puede interpretarse como se hizo en el ejemplo anterior: posiblemente sea un curso heterogéneo con estudiantes de distintos grados de interés o bien las preguntas de examen fueron de diferentes niveles de dificultad. El uso de una hoja de cálculo como Excel, facilita en gran medida la resolución de este tipo de problemas y también ofrece la opción de graficar la distribución