Estadística de la Calidad: Control de Procesos y Análisis Descriptivo
Anuncio
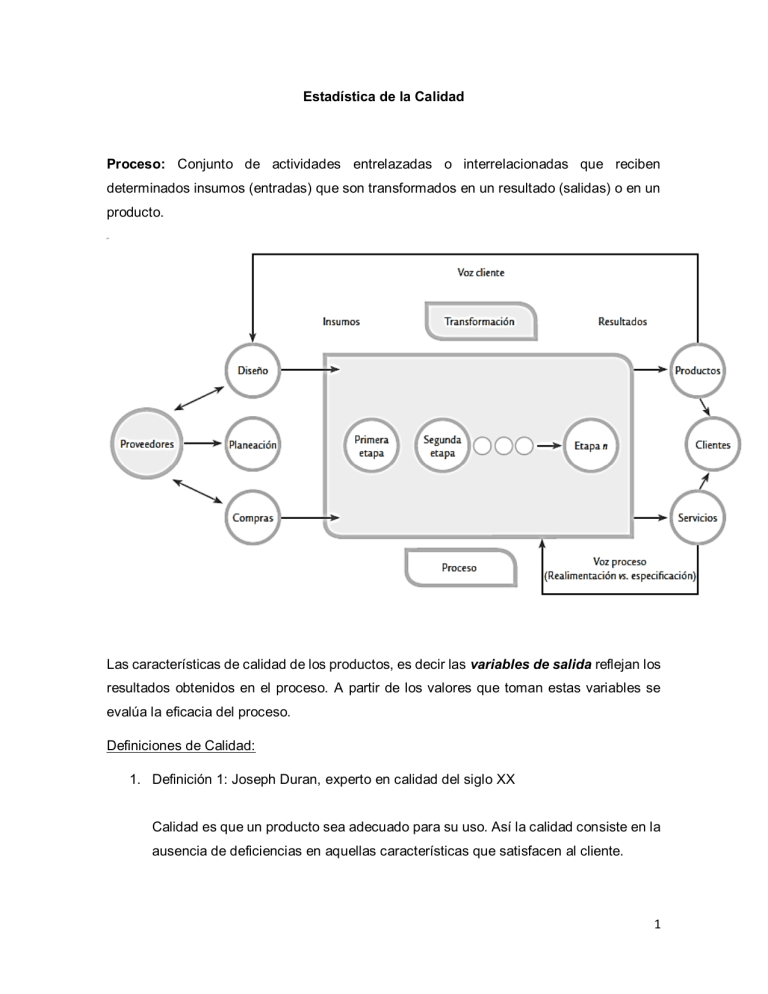
Estadística de la Calidad Proceso: Conjunto de actividades entrelazadas o interrelacionadas que reciben determinados insumos (entradas) que son transformados en un resultado (salidas) o en un producto. Las características de calidad de los productos, es decir las variables de salida reflejan los resultados obtenidos en el proceso. A partir de los valores que toman estas variables se evalúa la eficacia del proceso. Definiciones de Calidad: 1. Definición 1: Joseph Duran, experto en calidad del siglo XX Calidad es que un producto sea adecuado para su uso. Así la calidad consiste en la ausencia de deficiencias en aquellas características que satisfacen al cliente. 1 2. Definición 2: Sociedad Americana para la Calidad Calidad es la totalidad de detalles y características de un producto o servicio que influye en su capacidad para satisfacer necesidades. 3. Definición 3: Normas ISO La calidad se define como el grado en el que un conjunto de características inherent es cumplen con los requisitos. En términos menos formales, la calidad definida por el cliente, es el juicio que este tiene acerca de un producto o servicio. Factores críticos que afectan la satisfacción del cliente Calidad del producto Calidad del servicio Precio Competitividad de la empresa Control estadístico de procesos SPC (Statistical Process Control) Técnica que permite determinar si el resultado de un proceso concuerda con su diseño. Objetivo: Identificar y eliminar la variabilidad Variabilidad: Es la diferencia entre el desempeño real y el desempeño esperado Causas de la variabilidad Causas comunes: Fuentes de variación puramente aleatoria, no identificable e imposible de evitar mientras se utilice el procedimiento actual. Si la variabilidad del proceso proviene únicamente de causas comunes, la suposición es que se trata de una distribución simétrica. 2 Causas asignables: Factores de variación externos al proceso, se deben identificar y eliminarse. Se dice que un proceso está bajo control estadístico cuando: Solo existen causas comunes de variación Las causa asignables se han eliminado, aunque sea temporalmente El proceso es estable Bajo control estadístico la variable aleatoria sigue un modelo probabilístico que no cambia con el tiempo. Capacidad de procesos Las variables de salida deben cumplir con ciertas especificaciones, a fin de que sea posible considerar que el proceso funciona de manera satisfactoria. Por ello, una tarea primordial del control de calidad es conocer la capacidad o habilidad de un proceso, que consiste en determinar la amplitud de la variación natural del proceso para una característica de calidad dada. Esto permitirá saber en qué medida tal característica de calidad es satisfactoria. 3 Estadística descriptiva Medidas de tendencia central: Una medida de tendencia central es un valor único que resume un conjunto de datos. También señala el centro de los datos Media: Promedio aritmético de un conjunto de datos Media poblacional: Media muestral: μ= 𝑥̅ = ∑N i=1 xi 𝑁 ∑n i=1 xi 𝑛 Mediana (𝒙̃ 𝒐 𝑴𝒆) : Es una medida de tendencia central que divide el conjunto de datos en dos partes iguales después de ordenarlos, es decir el 50% de los datos tienen valores mayores a la mediana y el 50% de los datos tienen valores menores que la mediana. Moda: Es el valor del dato que aparece con mayor frecuencia Medidas de dispersión o variabilidad: Indican la variabilidad de un conjunto de datos. Indican que tan dispersos se encuentran los datos. Varianza: Promedio de las desviaciones cuadráticas respecto de la media. Varianza poblacional: σ2 = Varianza muestral: s2 = 2 ∑N i=1(xi −𝜇) 𝑁 2 ∑N i=1(xi −𝑥̅ ) 𝑛−1 Desviación estándar: Raíz cuadrada de la varianza Desviación estándar poblacional: Desviación estándar muestral: σ=√ s=√ 2 ∑N i=1(xi −𝜇) 𝑁 2 ∑N i=1(xi −𝑥̅ ) 𝑛−1 4 Ejercicio 1: Un banco lleva un registro de los minutos que los clientes esperan para ser atendidos; al azar se eligen 10 de estos tiempos de espera y se obtiene lo siguiente: 18.1 7.9 14.6 13.6 14.2 13.0 11.0 7.4 8.7 11.0 Relación entre medidas de tendencia central y medidas de dispersión Regla empírica: Si un conjunto de datos tienen una distribución simétrica entonces se ha observado por la experiencia que: Entre 𝑥̅ − 𝑠 𝑦 𝑥̅ + 𝑠 esta el 68% de los datos Entre 𝑥̅ − 2𝑠 𝑦 𝑥̅ + 2𝑠 esta el 95% de los datos Entre 𝑥̅ − 3𝑠 𝑦 𝑥̅ + 3𝑠 esta el 99,7 % de los datos Limites reales o naturales de proceso Los limites naturales de un proceso indican los puntos entre los cuales varia la variable de salida. Limite real inferior: 𝐿𝑅𝐼 = 𝑥̅ − 3𝑠 Limite real superior: 𝐿𝑅𝑆 = 𝑥̅ + 3𝑠 5 Histograma Un histograma es la representación gráfica, en forma de barras, de la distribución de un conjunto de datos o una variable, donde los datos se clasifican por su magnitud en cierto número de grupos o clases. Por lo general, el eje horizontal está formado por una escala numérica para mostrar la magnitud de los datos; mientras que en el eje vertical se representan las frecuencias. Pasos para la construcción de un histograma. 1. Calcular el valor del rango r = valor máximo – valor mínimo 2. Calcular el número de clases o intervalos en los que se va a resumir la información 𝑘 = 1 + 3.3 log10 𝑛 Aproximar k siempre a un entero 3. Calcular el ancho de clase i: 𝑖= 𝑟 𝑘 Aproximar al número mayor no necesariamente entero 4. Determina los límites de cada intervalo comenzando con el valor mínimo y adicionando el valor del ancho de clase i. 5. Realizar los conteos para establecer las frecuencias 6. Graficar los valores de la variable (intervalos) contra las frecuencias. Ejercicio 2 Excel 6 Formas comunes de los Histogramas 7 Medidas de forma: Las medidas de forma como su nombre lo indica, permiten conocer que forma tiene la curva que representa el conjunto de datos de la muestra o de la población. Coeficiente de asimetría: Permite determinar si la curva que forman el conjunto de datos tiene la misma forma a la izquierda y a la derecha de un valor central (generalmente la media) 𝑛 ∑𝑛𝑖=1(𝑥𝑖 − 𝑥̅ )3 𝐶𝐴 = (𝑛 − 1)(𝑛 − 2)𝑠 3 CA = 0 distribución simétrica (curva roja) CA > 0 distribución sesgada a la derecha (curva azul) CA < 0 distribución sesgada a la izquierda (curva verde) Asimetría estandarizada: 𝐶𝐴𝑒 = 𝐶𝐴 √ 6 𝑛 Para los datos que siguen una distribución normal, el valor de la asimetría estandarizada debe caer dentro de (−2, +2). Coeficiente de curtosis: Permite analizar el grado de concentración que presentan los valores alrededor de la zona central. 8 𝑛(𝑛 + 1) ∑𝑛𝑖=1(𝑥𝑖− 𝑥̅ )4 3(𝑛 − 1)2 𝐾= − (𝑛 − 1)(𝑛 − 2)(𝑛 − 3)𝑠 4 (𝑛 − 2)(𝑛 − 3) K = 0 la distribución es Mesocúrtica K > 0 la distribución es Leptocúrtica K < 0 la distribución es Platicúrtica Curtosis estandarizada: 𝐾𝑒 = 𝐾 √24 𝑛 Para los datos que siguen una distribución normal el valor de la curtosis estandarizada debe estar dentro de (−2, +2). Bibliografía Gutiérrez Pulido, H., & de la Vara Salazar, R. (2013). Control estadístico de la calidad y Seis Sigma. México DF: Mc Graw Hill Education. 9










