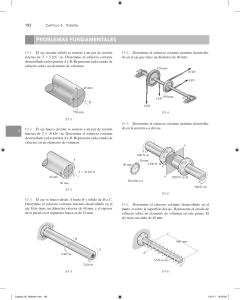
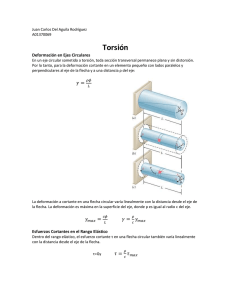
UNIVERSIDAD NACIONAL DE JAÉN CARRERA PROFESIONAL DE INGEN IERIA CIVIL RESOLUCIÓN DE EJERCICIOS “TORSIÓN” Curso: Mecánica De Los Materiales. Jaén-Perú Descargado por Yofre Hernández ([email protected]) Encuentra más documentos en www.udocz.com SOLUCIÓN DE EJERCICIOS 1. El tubo mostrado en la figura tiene un diámetro interior de 80mm y un diámetro exterior de 100mm. Si su extremo se aprieta contra el soporte en A mediante una llave de torsión en B, determine el esfuerzo cortante desarrollado en el material sobre las paredes interior y exterior, a lo largo de la posición central del tubo, al momento de aplicar las fuerzas de 80 N sobre la llave. SOLUCION: Realizamos el diagrama de cuerpo libre Descargado por Yofre Hernández ([email protected]) Encuentra más documentos en www.udocz.com Aplicamos el par de torsión interno ∑𝑀𝑦 =0 80𝑁(0.3𝑚) + 80𝑁(0.2𝑚) − 𝑇 = 0 𝑇 = 40𝑁. 𝑚 a) Propiedad de la sección El momento polar de inercia para la sección transversal del tubo es: 𝜋 𝐽 = (𝐶𝑜4 − 𝐶𝑖4 ) 2 𝜋 𝐽 = [(0.05𝑚)4𝑜 − (0.04)4𝑖 )] 2 𝐽 = 5.796(10−6 )𝑚4 b) esfuerzo cortante Para cualquier punto que se encuentre sobre la superficie exterior del tubo, 𝜌 = 𝑐𝑜 = 0.05𝑚 → 𝒯𝑂 = 𝑇𝑐𝑜 40𝑁. 𝑚(0.05𝑚) = = 0.345𝑀𝑃𝑎 5.796(10−6 )𝑚4 𝐽 Para cualquier punto situado a la superficie interior, 𝜌 = 𝑐𝑖 = 0.04𝑚. entonces para el diámetro interior del tubo es 𝒯𝑖 = 𝑇𝑐𝑖 40𝑁. 𝑚(0.04𝑚) = = 0.276𝑀𝑃𝑎 5.796(10−6 )𝑚4 𝐽 Descargado por Yofre Hernández ([email protected]) Encuentra más documentos en www.udocz.com 2. Un eje está hecho de una aleación de acero que tiene un esfuerzo cortante permisible de 𝒯𝑝𝑒𝑟𝑚 = 12 𝑘𝑠𝑖. Si el diámetro del eje es de 1.5 pulg, determine el par de torsión máximo T que se puede transmitir. ¿Cuál sería el par máximo 𝑇 ′ si se perforara un orificio de 1 pulg de diámetro a través del eje? SOLUCION: Aplicando la fórmula del esfuerzo cortante máximo en el eje: 𝑇𝑐 𝑇(0.75) 𝒯𝑚𝑎𝑥 = ⟶ 12 = 𝜋 4 𝑗 2 (0.75) ∴ 𝑇 = 7.95 𝑘𝑖𝑝. 𝑖𝑛 Aplicando la fórmula del esfuerzo cortante máximo en el eje: 𝑇𝑐 𝑇 ′ (0.75) 𝒯𝑚𝑎𝑥 = ⟶ 12 = 𝜋 𝑗 (0.754 − 0.54 ) 2 ∴ 𝑇 ′ = 6.38 𝑘𝑖𝑝 . 𝑖𝑛. Descargado por Yofre Hernández ([email protected]) Encuentra más documentos en www.udocz.com 3. El eje sólido de radio r está sometido a un par de torsión T. Determine el radio r ′ del núcleo interno del eje que resiste la mitad del par de torsión aplicado (T/2). Resuelva el problema de dos maneras: (a) utilizando la fórmula de la torsión, (b) buscando la resultante de la distribución del esfuerzo cortante. a) SOLUCION: Aplicando la fórmula del esfuerzo cortante máximo en el eje: 𝒯𝑚𝑎𝑥 = 𝑇(𝑟) 2𝑇 𝑇𝑐 ⟶ 𝒯𝑚𝑎𝑥 = 𝜋 ⟶ ∴ 𝒯𝑚𝑎𝑥 = 𝑗 𝜋(𝑟)3 (𝑟)4 2 𝑇 ′ (𝑟 ) 𝑇 𝑇𝑝 ⟶ 𝒯 = 𝜋2 ⟶∴ 𝒯 = 𝒯= 𝜋(𝑟 ′ )3 𝑗 (𝑟 ′ )4 2 Por relación de triángulos: 𝒯 𝒯𝑚𝑎𝑥 𝑝 𝑟′ = ⟶ ∴ 𝒯 = 𝒯𝑚𝑎𝑥 ⟶ ∴ 𝒯 = 𝒯𝑚𝑎𝑥 𝑝 𝑟 𝑐 𝑐 ⟶ 𝑇 𝑟 ′ 2𝑇 = ⟶ ∴ 𝑟 ′ = 0.841 r 𝜋(𝑟 ′ )3 𝑟 𝜋(𝑟)3 Descargado por Yofre Hernández ([email protected]) Encuentra más documentos en www.udocz.com b) SOLUCION: 𝜌 El par de torsión interno 𝑑𝑇 = 𝜌(𝒯𝑑𝐴) , 𝑑𝐴 = 2𝜋𝜌𝑑𝜌 y 𝒯 = ( ) 𝒯𝑚𝑎𝑥 𝑐 𝑇 2 𝑇 2 𝑟′ ∫ 𝑇 = 2𝜋 ∫ 𝒯𝜌2 𝑑𝑝 0 ∫ 𝑇 = 2𝜋 ∫ 0 𝑟′ 0 𝑇 2 ∫ 𝑇 = 2𝜋 ∫ 0 𝑟′ 0 4 0 𝜌 𝒯𝑚𝑎𝑥𝜌2 𝑑𝜌 𝑐 𝜌 2𝑇 2 𝜌 𝑑𝜌 𝑟 𝜋(𝑟)3 ′ 𝑇 4𝑇 𝑟 3 = 4 ∫ 𝜌 𝑑𝜌 2 𝑟 0 𝑟4 𝑟′ = ⟶ ∴ 𝑟 ′ = 0.841 r 4 8 4. El tubo se somete a un par de torsión de 750 N m. Determine qué porción de este par es resistido por la sección con sombreado más claro. Resuelva el problema de dos maneras: (a) mediante la fórmula de la torsión, (b) buscando la resultante de la distribución del esfuerzo cortante. SOLUCION: Aplicando la fórmula del esfuerzo cortante máximo en el eje: 𝑇𝑐 750(0.1) 𝒯𝑚𝑎𝑥 = ⟶ 𝒯𝑚𝑎𝑥 = 𝜋 𝑗 ((0.1)4 − (0.025)4 ) 2 ∴ 𝒯𝑚𝑎𝑥 = 0.4793 𝑀𝑝𝑎 Descargado por Yofre Hernández ([email protected]) Encuentra más documentos en www.udocz.com 𝑇 ′ (0.1) 𝒯𝑚𝑎𝑥 = 0.4793 𝑀𝑝𝑎 = 0.4793(106 ) 𝑝𝑎 = 𝜋 ((0.1)4 − (0.075)4 ) 2 ∴ 𝑇 ′ = 514,6 𝑁𝑚 𝜌 El par de torsión: 𝑑𝑇 = 𝜌(𝒯𝑑𝐴) , 𝑑𝐴 = 2𝜋𝜌𝑑𝜌 y 𝒯 = ( ) 𝒯𝑚𝑎𝑥 𝑇′ ∫ 𝑇 = 2𝜋 ∫ 0 𝑇 ′ = 2𝜋 ∫ 0.1 0.1 0.1 𝑐 𝒯𝜌2 𝑑𝑝 0.075 𝒯𝜌2 𝑑𝑝 0.075 𝜌 𝒯𝑚𝑎𝑥𝜌2 𝑑𝜌 𝑐 0.075 0.1 2𝜋𝒯𝑚𝑎𝑥 ∫ 𝜌3 𝑑𝜌 𝑇′ = 𝑐 0.075 4 ((0.1) 2𝜋𝒯𝑚𝑎𝑥 − (0.075)4 ) 𝑇′ = 𝑐 4 𝑇 ′ = 2𝜋 ∫ 2𝜋(0.4793(106 )) ((0.1)4 − (0.075)4 ) 𝑇 = 4 0.1 ∴ 𝑇 ′ = 514,6 𝑁𝑚 ′ 5. El tubo de cobre tiene un diámetro exterior de 40 mm y un diámetro interior de 37 mm. Si se asegura fuertemente a la pared en A y se le aplican tres pares de torsión como se muestra en la figura, determine el esfuerzo cortante máximo absoluto desarrollado en el tubo. De la figura sumatoria de momentos igual a 0: 80𝑁𝑚 − 20𝑁𝑚 + 30𝑁𝑚 − 𝑇 = 0 ∴ 𝑇 = 90𝑁𝑚 Descargado por Yofre Hernández ([email protected]) Encuentra más documentos en www.udocz.com Aplicando la fórmula del esfuerzo cortante máximo en el eje: 90(0.020) 𝑇. 𝑐 ⟶ 𝒯𝑚𝑎𝑥 = 𝜋 𝒯𝑚𝑎𝑥 = 𝑗 ((0.020)4 − (0.0185)4 ) 2 ∴ 𝒯𝑚𝑎𝑥 = 26,733 𝑀𝑝𝑎 6. El eje sólido tiene un diámetro de 0.75 pulg. Si se somete a los pares de torsión mostrados en la figura, determine el esfuerzo cortante máximo desarrollado en las regiones BC y DE del eje. Los cojinetes en A y F permiten que el eje gire libremente. 1𝑝𝑖𝑒 = 12 𝑝𝑢𝑙 De la figura corte en BC, encontramos el par de torsión BC: ∴ 𝑇𝐵𝐶 = 35 𝑙𝑏. 𝑝𝑖𝑒𝑠 = 35(12)𝑙𝑏. 𝑝𝑢𝑙 𝒯𝑚𝑎𝑥𝐵𝐶 = 𝑇𝐵𝐶𝑐 35(12)(0.375) ⟶ 𝒯𝑚𝑎𝑥𝐵𝐶 = 𝜋 𝑗 (0.375)4 2 ∴ 𝒯𝑚𝑎𝑥𝐵𝐶 = 5070𝑃𝑆𝐼 De la figura corte en DE, encontramos el par de torsión DE: ∴ 𝑇DE = 25 𝑙𝑏. 𝑝𝑖𝑒𝑠 = 25(12)𝑙𝑏. 𝑝𝑢𝑙 𝒯𝑚𝑎𝑥DE = 𝑇DE𝑐 25(12)(0.375) ⟶ 𝒯𝑚𝑎𝑥DE = 𝜋 ∴ 𝒯𝑚𝑎𝑥DE = 3621𝑃𝑆𝐼 𝑗 (0.375)4 2 Descargado por Yofre Hernández ([email protected]) Encuentra más documentos en www.udocz.com 7. El eje sólido de 30 mm de diámetro se utiliza para transmitir los pares de torsión aplicados a los engranes. Determine el esfuerzo cortante máximo absoluto en el eje. A partir del diagrama de par se deduce que: ∴ 𝒯𝑚𝑎𝑥 = 400 𝑁𝑚 Aplicando la fórmula del esfuerzo cortante máximo en el eje: 𝑇𝑐 400(0.015) 𝒯𝑚𝑎𝑥 = ⟶ 𝒯𝑚𝑎𝑥 = 𝜋 𝑗 (0.015)4 2 ∴ 𝒯𝑚𝑎𝑥 = 75451232 𝑃𝑎 ≅ 75,45 𝑀𝑃𝑎 Descargado por Yofre Hernández ([email protected]) Encuentra más documentos en www.udocz.com 8. El eje consiste en tres tubos concéntricos, cada uno hecho del mismo material y con los radios interior y exterior mostrados en la figura. Si se aplica un par de torsión T = 800 Nm sobre el disco rígido fijo en su extremo, determine el esfuerzo cortante máximo en el eje. Formula del momento polar de inercia del área de la sección transversal: ∴ 𝐽𝑡𝑜𝑡𝑎𝑙 = ∴𝐽= 𝜋 4 𝐶 2 𝜋 𝜋 𝜋 ((0.025)4 −(0.020)4 ) + ((0.030)4 −(0.026)4 ) + ((0.038)4 −(0.032)4 ) 2 2 2 ∴ 𝐽𝑡𝑜𝑡𝑎𝑙 = 2,545(10−6 ) 𝑚4 Aplicando la fórmula del esfuerzo cortante máximo en el eje: 𝑇𝑐 800(0.038) 𝒯𝑚𝑎𝑥 = ⟶ 𝒯𝑚𝑎𝑥 = 2,545(10−6 ) 𝑗 ∴ 𝒯𝑚𝑎𝑥 = 11,9 𝑀𝑃𝑎 Descargado por Yofre Hernández ([email protected]) Encuentra más documentos en www.udocz.com