1DistribucionesDiscretas

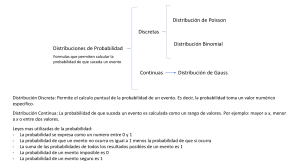
 Estadística Inferencial
Modelos de probabilidad
aleatorias discretas
para
variables
Bibliografía recomendada: Cordova, Manuel. 2003. Estadística:
Descriptiva e Inferencial. Ed. Moshera S.R.L. 5ta edición. Pp 202 278
2024-1
[email protected]
Variable aleatoria, variable estocástica, variable de
probabilidad, variante
Una variable aleatoria X es una función numérica que
asocia a cada suceso del espacio muestral E de un
experimento aleatorio un valor numérico real.
X :E →
Las v. a. se pueden clasificar en:
DISCRETAS, cuyo rango es un conjunto
finito o infinito numerable de valores.
Provienen de contar, solamente pueden ser
representados con números enteros.
CONTINUAS, cuyo rango es un conjunto
finito no numerable de valores. Provienen de
medir, se pueden representar con números
enteros o fraccionarios. Entre dos valores
siempre existe un numero intermedio.
Ejemplo de variable aleatoria discreta:
Número de caras al lanzar tres
monedas (fenómeno aleatorio).
Elementos del
espacio muestral
sucesos o
eventos
+++
++C +C+
C++
CC+
C+C
+CC CCC
Ley de
correspondencia
Números reales
(# de caras)
0
1
2
3 caras
Establecer una variable aleatoria para un experimento
aleatorio no es más que una forma de asignar de "manera
natural" números a los eventos. Tienen un número fijo de
valores.
n x
n!
n− x
B(n, p) = p( x) =   p (1 − p) =
p x (1 − p) n − x
x!(n − x)!
 x
En Excel: DISTR.BINOM.N(núm_éxito;ensayos;prob_éxito;acumulado)
Ejercicios.
1. Tasa de éxito en la venta de propiedades. Supongamos que una agencia inmobiliaria tiene
una tasa de éxito del 20% en la venta de propiedades residenciales. Si la agencia planea
promocionar 10 propiedades este mes, se puede utilizar la distribución binomial para
calcular la probabilidad de que vendan exactamente 2 propiedades.
2.Probabilidad de encontrar inquilinos para un conjunto de apartamentos. Un propietario
tiene un conjunto de 15 apartamentos que está tratando de alquilar. La tasa histórica de
ocupación de los apartamentos es del 75%. Si cada apartamento se trata como una prueba
independiente, se puede utilizar la distribución binomial para calcular la probabilidad de que
al menos 10 de los 15 apartamentos estén ocupados.
3.Probabilidad de éxito en la obtención de préstamos hipotecarios. Un banco otorga
préstamos hipotecarios con una tasa de aprobación del 90%. Si el banco procesa 20
solicitudes de préstamos hipotecarios este mes, se puede utilizar la distribución binomial
para calcular la probabilidad de que al menos 18 solicitudes sean aprobadas.
4.Supongamos que una agencia inmobiliaria tiene una tasa de éxito del 20% en la venta de
propiedades en un área determinada. Si la agencia intenta vender 10 propiedades en esa
área, se puede calcular la probabilidad de que exactamente 2 de esas propiedades se vendan
con éxito.
5. Una compañía de gestión de propiedades tiene una tasa de éxito del 30% en la búsqueda
de inquilinos para las propiedades que administra. Si la compañía intenta encontrar
inquilinos para 8 propiedades, se puede calcular la probabilidad de que al menos 5 de esas
propiedades encuentren inquilinos con éxito.
6.Probabilidad de problemas en contratos de arrendamiento. Se sabe que el 10% de los
contratos de arrendamiento de una agencia inmobiliaria tiene problemas legales. Si la
agencia administra 15 contratos de arrendamiento, se puede calcular la probabilidad de que
Ejercicios
1.Variable: Número de defectos en una serie de bloques de concreto. Supongamos
que se está construyendo un edificio y se toman muestras aleatorias de bloques de
concreto para inspeccionar su calidad. Sea X la variable aleatoria que representa el
número de defectos encontrados en un bloque seleccionado al azar. Si se sabe que la
distribución de X sigue una distribución de Poisson con una tasa de 0.5 defectos por
bloque, se puede calcular la probabilidad de encontrar exactamente 2 defectos en un
bloque aleatorio.
2.Número de días para completar una tarea de construcción. En un proyecto de
construcción, se sabe que la cantidad de días necesarios para completar una
determinada tarea sigue una distribución de probabilidad discreta. Sea Y la variable
aleatoria que representa el número de días necesarios para completar dicha tarea. Se
puede proporcionar una tabla de probabilidades de que la tarea tarde 1, 2, 3, o más
días en completarse y pedir calcular la probabilidad de que la tarea se complete en
menos de 4 días.
3.Cantidad de accidentes laborales en un sitio de construcción : En un sitio de
construcción, se registra el número de accidentes laborales ocurridos en un mes
determinado. Sea Z la variable aleatoria que representa el número de accidentes
laborales en un mes dado. Si se sabe que la distribución de Z sigue una distribución
binomial con una probabilidad de éxito del 5% (es decir, la probabilidad de que
ocurra un accidente en un día es del 5%) y se están trabajando 25 días en ese mes, se
Puede pedir calcular la probabilidad de que ocurran exactamente 2 accidentes en ese
período.
Distribución de probabilidad binomial
P(x~(n,p)); b(x;n;p); P(X=r|n,p)
La distribución binomial aparece cuando estamos
interesados en el número de veces (x) que un suceso
A ocurra (éxitos) en n intentos independientes.
Experimento: N° de caras obtenidas en n lanzamientos de
una moneda.
Si A tiene una probabilidad de éxito p en un
intento, entonces (1- p) es la probabilidad de que A
no ocurra (probabilidad de fracaso = q).
Ejemplo binomial. Experimento aleatorio, n = 3 lanzamientos de una
moneda. Probabilidad de éxito en cada lanzamiento (S) = p = .
Probabilidad de fracaso en cada lanzamiento (F) = 1- p = q.
S = Atributo (suceso) se obtiene cara, F = Atributo (evento) se obtiene cruz.
3 p 2 (1 − p )
3 p(1 − p) 2
Formula de la Distribución de Probabilidad Binomial
Supongamos que el experimento consta de n intentos y definamos la v. a.
X = Número de veces que ocurre A.
En nuestro ejemplo de la diapositiva anterior:
X = Número de veces que sale cara en los n intentos.
Entonces X puede tomar los valores: 0, 1, 2, ... n.
Si consideramos uno de estos valores, por ejemplo, en x de los n intentos
ocurre el suceso A y en (n – x) no ocurre A. Entonces la probabilidad de
n
cada posible combinación es pxqn-x y existen
idénticas
 
 x
combinaciones.
La función de probabilidad P(X = x) será la distribución de p. binomial:
n x
n!
n− x
B(n, p) = p( x) =   p (1 − p) =
p x (1 − p) n − x
x!(n − x)!
 x
En Excel: DISTR.BINOM.N(núm_éxito;ensayos;prob_éxito;acumulado)
Ejemplo 1.
En la Clínica «Romero y su Nieta» una décima parte de sus pacientes tiene
grupo sanguíneo «AB-»
a) ¿Qué modelo de distribución de probabilidad aplicarías?
b) ¿Cuál es la probabilidad de que, entre 100 pacientes escogidos al azar,
exactamente ocho de ellos pertenezcan a este grupo sanguíneo?
 n x
n− x
p(x) =   p ( 1 − p)
 x
p = 0,10;
n = 100;
x=8
 100 
8
92
 ( 0,1 ) ( 1 - 0,1 )
p( 8 ) = 
 8 
R. 11,42 %
Tarea redacta la Interpretación del resultado
c) Y si la pregunta anterior fuera ocho como máximo ¿cuál es la
probabilidad?
d) Y si la pregunta anterior fuera ocho como mínimo ¿cuál es la
probabilidad?
e) Y si la pregunta anterior fuera tres como mínimo y ocho como máximo
¿cuál es la probabilidad?
 n x
n− x
p(x  8 ) =    p ( 1 − p)
x=0  x 
8
 100 
x
100 − x
(0.1) ( 0.9 )
=  
x=0  x 
8
En Excel:
DISTR.BINOM.SERIE(ensayos;prob_éxito;núm_éxitos;[núm_éxitos2])
Enlace para resolver ejercicios de Binomial
Distribucion binomial. Ejercicio resuelto 2 - Bing video
Ejemplo 2. Calcula la probabilidad de obtener al menos dos
veces “6” al lanzar un dado cuatro veces.
𝑃(𝑥) =
𝑛 𝑥 𝑛−𝑥
𝑝 𝑞
𝑥
(𝑥 = 0,1, . . . . 𝑛)
p = 1/6, q = 5/6, n = 4
Al menos dos “6”, implica x = 2; 3 y 4.
= P(2) + P(3) + P(4)
 4  1   5   4  1   5   4  1 
=      +      +   
 2  6   6   3  6   6   4  6 
2
2
3
4
1
171
= 4 (6 * 25 + 4 * 5 + 1) =
= 0,132 = 13,2%
1296
6
Tarea redacta la Interpretación del resultado
Características de la distribución binomial
Media:
Caso 1:
 = E(X) = n p
P(X) n = 5 p = 0.1
0.6
0.4
0.2
0.0
0
1
2
3
4
5
Caso 2:
1= 5 * 0,1 = 0,50 (Caso 1)
2= 5 * 0,5 = 0,25 (Caso 2)
Desviación estándar:
 = np(1 − p)
 1 = 5 * 0,1 * (1 − 0,1) = 0,67
 2 = 5 * 0,5 * (1 − 0,5) = 1,1
P(X)
.6
.4
.2
0
X
n = 5 p = 0.5
X
0
1
2
3
4
5
Ejercicios.
1) La compañía de seguros Arroz con Mango garantiza el pago de las pólizas de
seguros individuales contra retrasos aéreos de más de doce horas. Una encuesta ha
permitido estimar a lo largo de un año que cada persona tiene una probabilidad de
uno cada mil de ser víctima de un retraso aéreo que esté cubierto por este tipo de
póliza y que la compañía aseguradora podrá vender una media de cuatro mil pólizas
al año. Halla las siguientes probabilidades:
a) Que el número de retrasos cubiertos por la póliza no pase de cuatro por año.
b) Que el número de retrasos sea superior a dos por año.
c) Que ocurran doce retrasos por año.
R. (a) 62,88%; (b) 76,2%; (c) 0,0637%
2) Supón que la probabilidad de tener una unidad defectuosa en una línea de
ensamblaje de las plumas (flechas) de las grúas pórtico es de 5%. Si el conjunto de
unidades terminadas constituye un conjunto de ensayos independientes, contesta:
a) ¿cuál es la probabilidad de que entre diez unidades dos se encuentren
defectuosas?
b) ¿y de que a lo sumo dos se encuentren defectuosas?
c) ¿cuál es la probabilidad de que por lo menos una se encuentre defectuosa?
R. 7,46%; 98,84% y 40,13% respectivamente
Distribución de probabilidad de Poisson
X~p(λ); X~p(µ)
Un proceso poissoniano es aquél compuesto por eventos
discretos que son independientes en el espacio y/o en el
tiempo.
λ (lamda) es un parámetro positivo y real que representa el
número de veces que se espera que ocurra el fenómeno durante
un intervalo dado; otros autores la denominan «µ».
En este tipo de experimentos los éxitos buscados son expresados
por unidad de distancia, de área, de volumen, de tiempo, por
pieza, etc.
Ejemplos de λ:
- Número promedio de defectos por m2 de una tela sintética
- Cantidad de aviones que aterrizan en un aeropuerto por día.
- Número de bacterias por cm3 de cultivo
- Periodicidad de llamadas telefónicas a un conmutador por
hora.
- Número medio de llegadas de embarcaciones a un puerto por
Distribución de p Poisson…
Un proceso de Poisson es estacionario, la media (λ) del
proceso siempre es proporcional a la magnitud del conjunto
de tiempo o de espacio. Por tanto, si la media de que se
disponga corresponde a un determinado periodo, para otro
periodo que se requiera puede determinarse la media.
.
Por ejemplo, si el suceso estudiado tiene lugar en promedio
4 veces por minuto y estamos interesados en la probabilidad
de que ocurra x veces dentro de un intervalo de 10 minutos,
usaremos un modelo de distribución de Poisson con λ = 10*4
= 40 veces cada 10 minutos.
𝑒 −𝜆 𝜆𝑥
𝑒 −𝜇 𝜇 𝑥
𝑝(𝑥) =
=
, 𝑥 = 0; 1; 2; . . .
𝑥!
𝑥!
Donde:
e = 2,718281…
𝜆>0
Características de la distribución de Poisson
Media
Nota: el máximo de la distribución
se encuentra en x  
E (X) =  = 
Varianza
2 = 
Desviación estándar
 = 
Media y varianza Coinciden numéricamente aunque por supuesto μ está
expresada en unidades lineales y σ2 en
unidades cuadráticas.
 = 0.5
P(X)
.6
.4
.2
0
X
0
1
2
3
4
5
=6
P(X)
.6
.4
.2
0
X
0
2
4
6
8
10
Distribución de Poisson | Ejercicios resueltos | Intro - Bing video
Ejemplo 2. Si en promedio, entran dos coches por minuto en un
taller, ¿cuál es la probabilidad de que durante un minuto entren
cuatro o más coches? Solución:
μ x −μ
p( x) =
e
x!
( x = 0; 1;...)
El suceso complementario “entran 3 coches o menos” tiene
probabilidad:
−2 20
0!
P( A )  p(0) + p(1) + p(2) + p(3) = e ( + +
c
21
1!
22
2!
+ ) = 0,857
23
3!
y la respuesta para cuatro o más coches es 1 – 0,857 = 14,3%
Ejercicios.
1) La empresa electrónica Elba Lazo observa que el número
de componentes que fallan antes de cumplir 100 horas de
funcionamiento es una variable aleatoria de Poisson. Si el
número promedio de estos fallos es ocho, responde:
a) ¿cuál es la probabilidad de que falle un componente en
25 horas?
b) ¿y de que fallen no más de dos componentes en 50
horas?
c) ¿cuál es la probabilidad de que fallen más de diez en 125
horas?
R. 27,067%; 23,81% y 41,696% respectivamente.
2) Sabemos que el número de goles que se meten en un
partido de fútbol de la Premier League Interfacultades
UNMSM sigue una distribución de parámetro λ=2. ¿Cuál es
la probabilidad de que el próximo partido, entre la Facu y la
FIS se marquen en total 8 goles? R.
x = 8 λ = 2 P(x=8) = ≈ 0,00086 = 0,0%86%
3) El promedio de automóviles que usan una autopista un fin de semana
es de 4,5 por minuto. Cuál es la probabilidad de que usen la autopista:
a) Exactamente seis autos en un minuto.
b) A lo más dos automóviles en un tercio de minuto.
c) Por lo menos tres automóviles en el transcurso de los siguientes
30 segundos.
4) Se estima que el número promedio de comercios por manzana en
San Juan de Zafarrancho es de 5. Halla la probabilidad de que se
tengan tres comercios:
a) En una manzana.
b) En tres cuartos de manzana.
5) En el Torneo de Clausura 2020, hasta la fecha 16, Universitario en
promedio, anotó 1,69 goles por cada 90 minutos. De acuerdo con
esto:
a. ¿Cuál es la probabilidad de que la U anote dos goles en los
próximos 90 minutos?
b. ¿Cuál es la probabilidad de que la U anote cuando mucho un gol
durante el primer tiempo?
Propiedad reproductiva de las distribuciones de
probabilidad
Algunas distribuciones de probabilidad tienen la
propiedad siguiente:
Si dos o más variables aleatorias que tienen
una distribución de probabilidad del mismo tipo
se suman, la v. a. resultante tiene una distribución del mismo tipo que los sumandos.
(Teorema de Fourier).
Las distribuciones: Binomial (respecto a n),
Poisson (respecto a λ) y Normal (respecto a µ y
σ) son distribuciones reproductivas.
Ejemplo.
Si X1, X2, … , Xn son v.a. independientes de
Poisson con parámetros λ1, λ2, … λn, entonces:
n
Y =  Xi
i =1
Es una v.a. de Poisson con parámetro λy:
n
 y =  i
i =1
Ejemplo. El número medio de llamadas por segundo a la central telefónica
de la empresa Me Llega al Twitter es 7. Si existen 5 centrales de este tipo
¿cuál es la probabilidad de que en un segundo se reciban más de
40 llamadas?
P(X > 40) con µ = 35
Ejercicio.
En la fábrica Alan Brito SAC el número de accidentes
laborales por semana sigue un proceso de Poisson con
parámetro µ = 2. Determina:
a) La p. de que haya cuatro accidentes en el transcurso
de una semana
b) La p. de que haya cuatro accidentes en el transcurso
de tres semanas. R. 13,39%
Tip. ¿Se aplica propiedad reproductiva o propiedad
estacionaria?
c) La p. que haya dos accidentes en una semana, y
otros dos accidentes en la semana siguiente. R. 7,33%
Tip. Probma tipo.
d) Es lunes, y ya ha habido un accidente. La p. que en
aquella semana no haya más de tres accidentes. R.
83,48%
𝑃(𝑋 ≤ 3 ∣ 𝑋 ≥ 1) =
𝑃 𝑋 =1 +𝑃 𝑋 =2 +𝑃 𝑋 =3
Propiedad reproductiva de la binomial. La suma de v. a. binomiales,
cada una con el mismo parámetro p, es una binomial de parámetro p.
Ejemplo.
En el Hospital Romeo la probabilidad de curar un enfermo sin secuelas es 0,90. Esta
probabilidad es análoga en el Hospital Julieta. Si llegan en un día 20 enfermos al primer
hospital y 30 al segundo ¿cuál es la probabilidad de curar, sin ningún tipo de secuela,
a más de 46 pacientes?
Observa que se ha introducido una nueva v.a. en el experimento aleatorio. La v.a. Y
que es la suma de dos v. a. X.
Nos piden:
P(Y > 46) = P(X = 47) + P(X = 48) + P(X = 49) + P(X = 50) = 25%
Explicación: La v. a. Y sigue el modelo Binomial. Como n > 30 se puede resolver por el
modelo Normal.
Propiedad reproductiva…
La propiedad reproductiva de la distribución binomial establece que si tienes una
secuencia de ensayos independientes, todos con la misma probabilidad de éxito
p, y deseas calcular la probabilidad acumulada de un número específico de
éxitos en todos esos ensayos, puedes descomponer el problema en pasos más
pequeños. Aquí tienes dos ejercicios relacionados con la propiedad reproductiva
de la distribución binomial en el sector de la construcción:
1. **Probabilidad de rechazo de materiales**:
En una fábrica de materiales de construcción, se sabe que la probabilidad de
que un lote de materiales sea rechazado debido a defectos es del 5%. Si se
producen 10 lotes de materiales independientes, se puede calcular la
probabilidad de que exactamente 2 de los lotes sean rechazados.
Tip.
Utilizando la propiedad reproductiva de la distribución binomial, podemos
descomponer este problema en 10 ensayos independientes, cada uno con una
probabilidad de éxito del 5%.
Propiedad reproductiva…
2. **Probabilidad de fallos en inspecciones de seguridad**:
En un proyecto de construcción, se realizan 15 inspecciones de seguridad
independientes. Se sabe que la probabilidad de que una inspección de
seguridad falle debido a violaciones es del 10%. Calcular la probabilidad de que
al menos 3 inspecciones fallen.
Tip:
Utilizando la propiedad reproductiva de la distribución binomial, podemos
descomponer este problema en 15 ensayos independientes, cada uno con una
probabilidad de éxito del 10%. Entonces, la probabilidad de que al menos 3
inspecciones fallen es la suma de las probabilidades de 3 o más éxitos:
Propiedad reproductiva de la distribución de Poisson:
1. **Número de accidentes por día en diferentes zonas de un sitio de construcción**:
En un sitio de construcción hay tres zonas diferentes donde se registran accidentes de
manera independiente. En la zona A, se registra un promedio de 2 accidentes por día; en la
zona B, 3 accidentes por día; y en la zona C, 1 accidente por día. Si se divide el día en tres
intervalos de tiempo (mañana, tarde y noche), podemos utilizar la propiedad reproductiva de
la distribución de Poisson para calcular la probabilidad de que, en cada intervalo de tiempo,
ocurran exactamente cierto número de accidentes en cada zona.
2. **Número de inspecciones exitosas en diferentes etapas de un proyecto de construcción**:
En un proyecto de construcción se realizan inspecciones en tres etapas diferentes: inicio,
medio y final. En cada etapa, el número promedio de inspecciones exitosas por día es 5, 7 y
4 respectivamente. Utilizando la propiedad reproductiva de la distribución de Poisson,
podemos calcular la probabilidad de que en cada etapa ocurran exactamente cierto número
de inspecciones exitosas por día.
3. **Número de entregas de materiales por hora en diferentes áreas de un sitio de
construcción**:
Imagina que en un sitio de construcción hay tres áreas diferentes donde se realizan
entregas de materiales, y en cada área se realiza un promedio de 4, 3 y 6 entregas por hora
respectivamente. Utilizando la propiedad reproductiva de la distribución de Poisson, se puede
calcular la probabilidad de que, en cada área, ocurran exactamente cierto número de
entregas por hora en un período de tiempo específico.
Estos ejercicios demuestran cómo la propiedad reproductiva de la distribución de Poisson
puede aplicarse en diferentes escenarios del sector de la construcción para calcular la
probabilidad de eventos específicos en subconjuntos de un proceso general.