SIM 2PC CEPRE UNI 2024 2

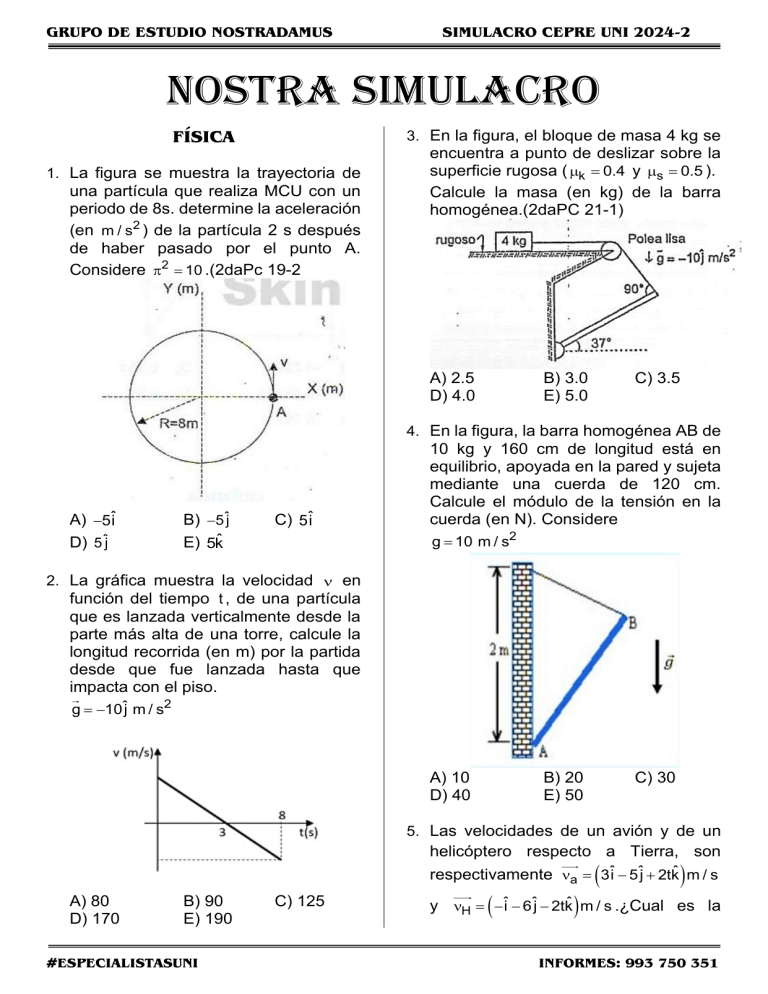
GRUPO DE ESTUDIO NOSTRADAMUS
SIMULACRO CEPRE UNI 2024-2
Nostra SIMULACRO
FÍSICA
3. En la figura, el bloque de masa 4 kg se
1. La figura se muestra la trayectoria de
una partícula que realiza MCU con un
periodo de 8s. determine la aceleración
(en m / s2 ) de la partícula 2 s después
de haber pasado por el punto A.
Considere 2 = 10 .(2daPc 19-2
encuentra a punto de deslizar sobre la
superficie rugosa ( k = 0.4 y s = 0.5 ).
Calcule la masa (en kg) de la barra
homogénea.(2daPC 21-1)
A) 2.5
D) 4.0
B) 3.0
E) 5.0
C) 3.5
4. En la figura, la barra homogénea AB de
A) −5iˆ
D) 5 ˆj
B) −5 ˆj
E) 5kˆ
C) 5iˆ
10 kg y 160 cm de longitud está en
equilibrio, apoyada en la pared y sujeta
mediante una cuerda de 120 cm.
Calcule el módulo de la tensión en la
cuerda (en N). Considere
g = 10 m / s2
2. La gráfica muestra la velocidad  en
función del tiempo t , de una partícula
que es lanzada verticalmente desde la
parte más alta de una torre, calcule la
longitud recorrida (en m) por la partida
desde que fue lanzada hasta que
impacta con el piso.
g = −10ˆj m / s2
A) 10
D) 40
B) 20
E) 50
C) 30
5. Las velocidades de un avión y de un
helicóptero respecto a Tierra, son
(
)
respectivamente a = 3iˆ − 5ˆj + 2tkˆ m / s
A) 80
D) 170
B) 90
E) 190
#ESPECIALISTASUNI
C) 125
(
)
y H = −ˆi − 6ˆj − 2tkˆ m / s .¿Cual es la
INFORMES: 993 750 351
GRUPO DE ESTUDIO NOSTRADAMUS
rapidez ( en m/s) del helicóptero
respecto al avión en el instante t = 2 s ?
A) 3
B) 6
C) 9
D) 98
E) 101
6. El vector posición de una partícula
(
)
viene dado por r = t 2 + t + 1 ˆi + (1 − 3t ) ˆj
en unidades del SI, siendo t el instante
de tiempo (en s). Determine la
veracidad o falsedad de las siguientes
proposiciones.
I. La aceleración de la partícula es
constante e igual a 2 î m / s2 .
II. La velocidad de la partícula en el
(
)
instante t = 0 s es o = ˆi − 3ˆj m / s .
III. La partícula realiza una trayectoria
parabólica.
A) VVV
B) VVF
C) VFV
D) FVV
E) FFF
7. En la figura se muestra la trayectoria de
una particula en MCUV, Al pasar por la
(
)
posición r = −3iˆ + 4ˆj m , su aceleración
es a = 2.7ˆi m / s2 y su rapidez esta
aumentando. Determine el ángulo que
forma la velocidad y la aceleración en
()
la posición descrita r .
SIMULACRO CEPRE UNI 2024-2
QUÍMICA
8. Dadas las siguientes proposiciones
referidas a la configuración electrónica
de
iones
y
sus
propiedades
magnéticas.
I. El ion 22Ti2 + frente a un campo
magnético externo experimenta una
aparente perdida de masa.
II. El ion 22Ti2 + y el ion 23V 3 + son
isoelectrónicos, y frente a un campo
magnético externo, experimentan
una aparente ganancia de masa.
III. La configuración electrónica de ion
3+
presenta anomalía al
25 Mn
principio de construcción (aufbau).
Son correctas:
A) I y III
B) II y III
C) Solo II
D) Solo III
E) I, II y III
9. Las propiedades de una sustancia
dependen de su composición, tipo de
enlace y estructura. Indique verdadero
(V) o falso (F) según corresponda a las
proposiciones que están referidas al
compuesto, cuya estructura de Lewis
es:
X
2+


2 :Y:


−
El elemento X puede estar ubicado en
el grupo IIA.
Y es un elemento del grupo IIA.
El compuesto mostrado no conduce la
corriente eléctrica en estado sólido.
A) FFV
B) VFV
C) VVF
D) VVV
E) FVV
10. Determine
los posibles números
cuánticos de un electrón que ocupa el
ultimo nivel de un átomo cuyo núcleo
contiene 47 protones.
1
2
1
D) 5,0,0, +
2
1
E) 6,0,0, +
2
A) 4,0,0, −
A) 16º
D) 53º
B) 37º
E) 74º
#ESPECIALISTASUNI
C) 45º
1
2
1
D) 5,2, +1, −
2
B) 5,1, −1, +
INFORMES: 993 750 351
GRUPO DE ESTUDIO NOSTRADAMUS
11. El cobre, es el elemento químico de
numero atómico 29. Se trata de un
metal de transición de color rojizo, con
brillo metálico y buen conductor
eléctrico. Desarrolle su configuración
electrónica y determine la alternativa
Incorrecta:
A) Presenta un total de 12 e− en
subniveles tipo “ p ”.
B) El subnivel “ 3d ” esta lleno.
C) Su catión divalente posee un
electrón desapareado.
D) Su Configuración electrónica es
estado basal es  Ar  4s2 3d9 .
E) En la configuración electrónica del
átomo neutro sus electrones en los
subniveles tipo “ s ” son siete.
12. Respecto a la Tabla Periódica Moderna
(TPM),
marque
la
alternativa
Incorrecta.
A) La ley periódica fue propuesta por
Moseley, donde los elementos están
ordenados de acuerdo a su numero
atómico (Z) creciente.
B) Está constituida de 18 columnas y 7
periodos
C) Según la configuración electrónica
los elementos se ubican en los bloques
“s”, “d” o “f” de la TPM.
D) Los elementos representativos
pertenecen al bloque “d”.
E) La configuración terminal ns2
corresponde a la columna 2 de la Tabla
Periódica; es decir, a la familia de los
alcalinos Térreos.
13. Considerando que el paramagnetismo
es la propiedad de ser atraído
débilmente por un campo magnético
externo, ¿Cuál de las siguientes
alternativas contiene a la especie de
mayor paramagnetismo?
+
A) 23V( s )
B) 26 Fe2ac
( )
C) 42 Mo( s )
+
E) 29 Cu2ac
( )
#ESPECIALISTASUNI
+
D) 26 Fe3ac
( )
SIMULACRO CEPRE UNI 2024-2
14. ¿Qué enunciados son correctos para
los halógenos del 9 F al 53I en ese
sentido?
Aumenta el carácter no metálico
La primera energía de Ionización
disminuye.
El radio atómico aumenta.
A) I y II
B) I y II
C) II y III
D) solo I
E) I, II y III
ARITMÉTICA
15. Responde verdadero (V) o falso (F)
según corresponda
I. Si al precio de un articulo se le
aumenta
el
y
luego
10%
sucesivamente se le descuenta el
10% , entonces el precio no varía.
II. Si un capital de le deposita a una
tasa nominal anual del 10%
capitalizable
semestralmente
durante un año, entonces la TEA
(tasa efectiva anual) es 10,25% .
III. Para un letra que vence en t años y
descontada al r% anual tanto
comercialmente
como
racionalmente, se cumple que la
razón
geométrica
entre
los
descuentos comercial y racional (en
dicho orden) es igual a (1 + r%  t )
A) VFF
B) VVF
C) VVV
D) FVV
E) FFF
16. Para fijar el precio de un artículo, el
costo se aumento en su doble, al
momento de venderlo se hicieron dos
descuentos sucesivos del 20% y 20% .
Si los gastos de venta y ganancia bruta
están en relación de 1 a 5. Determine
en qué relación se encuentran el precio
de venta y la ganancia neta (considere
IGV = 18% del valor de venta)
177
115
256
C)
115
354
E)
115
A)
192
115
283
D)
115
B)
INFORMES: 993 750 351
GRUPO DE ESTUDIO NOSTRADAMUS
17. Se reparte cierta cantidad en 3 partes
DP a los números b, c y d y a la vez IP
a los números a, b y c. Se observa que
las tres partes obtenidas en el reparto
son iguales. Si a + d = 261 y a + b es un
numero natural, calcule b + c .
A) 125
B) 174
C) 185
D) 194
E) 204
SIMULACRO CEPRE UNI 2024-2
II. a  0,b  0 , entonces a2 − ab  0 .
III. Si a  0,b  0 , entonces
A) FVV
D) VFF
19. Se sabe que en un banco un capital
genera un interés que es la tercera
parte del monto con capitalización
trimestral en 3 años. Indique la tasa
anual (use 12 1.5 = 1,0343 )
A) 13,72 %
B) 15,2 % C) 24,4 %
D) 26,2 %
E) 28,8 %
20. Una persona A forma una empresa con
10000 soles, a los 2 meses se asocia
con otra persona B y esta aporta 16000
soles, 3 meses más tarde, la persona A
retira 5000 soles; y 3 meses más tarde,
B retira 6000 soles de capital. Si al año
de haber iniciado la empresa, se
reparten utilidad de 221000 soles.
¿Cuánto le corresponde de utilidad al
socio A?
A) 51000
B) 57000 C) 68000
D) 78000
E) 85000
ÁLGEBRA
#ESPECIALISTASUNI
C) FFV
( x − 2)a ( x − 3 )b  0
( x − 4 )c
Se obtiene como solución al conjunto
−;2  3  4; + . Indique el mínimo
valor de T = a + b + c ( a,b,c  )
A) 3
B) 4
C) 6
D) 7
E) 10
23. En que intervalo debe variar k de modo
que una de las raíces reales de
x 2 − x − k = 0 , se encuentra en el
intervalo 3;6 ?
A) 1;10
B) 2;11
C) 3;6
D) 4;15
E) 6;30
24. Halla la suma de los valores enteros
que satisfacen la inecuación.
x − 2 + 2x  − x
A) -3
D) -5
B) -10
E) -7
C) -12
25. En la ecuación bicuadrática siguiente:
(
b
a
−1
−3
2
a − 13 x
+ b − a x3 + b = 0
)
(
)
Se cumple que 3a − 2b  12 .
Si x1,x2,x3,x 4 son sus raíces, halle el
valor de T = x14 + x 24 + x34 + x 44
A) 9
D) 23
B) 12
E) 41
C) 14
26. Determine el conjunto solución de
1− x + 1+ x  x
21. Indique el valor de verdad de las
siguientes proposiciones:
I. Si
a b 0,
a2  b2 ( a,b  ) .
B) FFF
E) VVV
22. Al resolver la inecuación
18. Se impone un mismo capital, cada mes,
a interés simple de la siguiente manera:
El primer mes al 5% mensual, el
segundo mes al 6% mensual, el tercer
mes al 7% mensual, y así
sucesivamente durante “n” meses. Si al
cabo de ese tiempo se produjo un
interés que es igual al 45% del capital,
determine el valor de “n”.
A) 4
B) 5
C) 6
D) 8
E) 9
b +1 1
 .
a
a
entonces
A) 0;+
B) 0;1
D) 
E)
1
C) 0; 
2
INFORMES: 993 750 351
GRUPO DE ESTUDIO NOSTRADAMUS
GEOMETRÍA
27. En un triángulo ABC, se traza la
ceviana BD , en el exterior relativo al
lado AB se ubica el punto E, tal que los
ángulos ABE y DBC son rectos. Si los
triángulos ABE y CBD son congruentes
y mEBC = 150 , entonces la medida
del ángulo BAE es
A) 15
B) 20
C) 25
D) 30
E) 34
28. Indique el valor de verdad de las
siguientes proposiciones:
I. En todo cuadrilátero inscrito en una
circunferencia la suma de las
medidas de los ángulos opuestos es
180.
II. Las cuerdas equidistantes del centro
de una circunferencia son paralelas.
III. En una circunferencia se tiene dos
cuerdas de diferente longitud, la
cuerda de mayor longitud es la que
esta más distante del centro
A) FFF
B) VFF
C) FVV
D) VFV
E) VVV
SIMULACRO CEPRE UNI 2024-2
30. En un cuadrilátero convexo ABCD, se
ubica el punto P en la diagonal AC tal
que
AP = BC ,
SI
mAPD = mBCA = 2m PCD .
entonces
la
BP = 6 u ,
longitud (en u) de AD es
A) 5
D) 8
B) 6
E) 12
C) 7
31. En un polígono de n lados, desde
(n − 9) vértices consecutivosm se han
trazado en total 2 (n + 1) diagonales.
Calcule el número de lados del
polígono.
A) 10
B) 11
C) 12
D) 15
E) 18
32. Los radios de dos circunferencias
miden 5 u y 20 u y la longitud del
segmento tangente común exterior es
12 3 . Calcule la distancia (en u) entro
los centros de las circunferencias.
A) 20
B) 21
C) 24
D) 25
E) 27
TRIGONOMETRÍA
29. En la figura ABCD es un cuadrado, BD
es un arco de circunferencia de centro
A y MN es tangente al arco BD en T. SI
AB − MN = a , entonces la longitud del
radio de la circunferencia inscrita en el
triángulo MCN es
33. En un triángulo ABC con vértices
A ( −4; 3 ) , B ( −1; 7 ) y C ( 5; −2) determine
la ecuación de la recta que pasa por el
vértice A e intersecta al lado BC en el
punto P, dividiendo al triángulo ABC en
dos regiones que están en la relación
de 4 a 5, siendo el triángulo ABP
de menor región.
A) y = 1
B) y = 2
C) y = 3
D) y = 4
E) y = 5
34. Un niño se encuentra a 200 m de una
( 2 − 1)
D) a ( 3 + 1)
A) a
( 3 − 1) A) a
E) a ( 2 + 1)
B) a
#ESPECIALISTASUNI
torre en un mismo plano vertical y
observa la parte superior de la torre con
un ángulo de elevación de 82°. Luego
retrocede 500 m y observa la parte
superior de la torre con un ángulo de
elevación
Calcule el valor
.
aproximado de tan .
INFORMES: 993 750 351
GRUPO DE ESTUDIO NOSTRADAMUS
A) 2
B) 3
1
2
E) 1
D)
C)
SIMULACRO CEPRE UNI 2024-2
38. En la figura se muestra el trapecio
rectángulo ABCD, donde CD = L ,
mDBC =  , determine EF en términos
de L,  y  .
3
2
35. En la figura mostrada, si el punto G es
baricentro del triangulo ABC, AO = OB ,
B = ( 3;4 ) y C = ( 5; −6 ) , calcule:
tan (  ) + cot (  )
L
tan (  ) cot (  ) + 1
L
B)
tan (  ) tan (  ) + 1
L
C)
cot (  ) cot (  ) + 1
L
D)
cot (  ) tan (  ) + 1
L
E)
tan (  ) + cot (  )
A)
67
30
74
E) −
30
61
30
73
D) −
30
C) −
B) −
A) −
71
30
HISTORIA
36. Si  es un ángulo en posición normal y
cumple la condición :
cos  + cos  − 2 = 1 y tan ( )  0 .
Calcule sen ( ) − cot ( )
A) −
C) −
E)
37. Si
1
B) −
2 3
5
D)
2 3
7
3
2 3
1
2 3
2 3

 2
;
6 3
y
6sen ( ) + 4 = k − 2 ,
calcule el menor valor de k
A) 8
B) 9
C) 10
D) 11
E) 12
#ESPECIALISTASUNI
39. La Edad de Piedra se divide en tres
periodos, establezca la relación
correcta de acuerdo a sus principales
características
I. Paleolítico
II. Mesolítico
III. Neolítico
a.
Surgimiento
del
excedente
productivo
b. Se desarrolló la horticultura y el
pastoreo
c. Se desarrolló
la evolución
del género humano
A) Ic – IIa – IIIb
B) Ia – IIc – IIIb
C) Ic – IIb – IIIa
D) Ib – IIa – IIIc
E) Ia – IIb – IIIc
INFORMES: 993 750 351
GRUPO DE ESTUDIO NOSTRADAMUS
40. Respecto a la adaptación y evolución
que alcanzo el genero Homo,
establezca la relación correcta entre la
especie y el logro cultural respectivo.
I. Homo neanderthal
II. Homo habilis
III. Homo erectus
a. usó el fuego y fue el primero en salir
de África
b. realizo los primeros rituales
funerarios
c. inicio la producción de herramientas
líticas
A) Ib, IIa, IIIc
B) Ic, IIa, IIIb
C) Ia, IIc, IIIb
D) Ib, IIc, IIIa
E) Ic, IIb, IIIa
41. Identifique la verdad (V) o falsedad (F)
de
los
siguientes
enunciados
correspondientes al periodo litico de
nuestra historia.
I. Los restos del hombre de Paiján
fueron enterrados con diversos
instrumentos musicales.
II. El taller litico de Chivateros permitió
la elaboración de puntas de lanza.
III. Las pinturas rupestres tienen
presencia de humanos en caceria.
IV. Las herramientas líticas más
antiguas ubicadas en Perú están
relacionados a Pikimachay.
A) VFFF
B) VVFV
C) VFFV
D) FVVV
E) FVVF
42. El Arcaico. inferior fue un periodo de
transición donde se experimentaron
cambios graduales. Con relación a esta
etapa, determine el valor de verdad (Vo
F) de los siguientes enunciados.
I. Desarrollo
de
las
primeras
manifestaciones de horticultura
II. Predominio de actividades como la
caza y la recolección
III. Aparición de la monumental en la
costa arquitectura
IV. Domesticación
inicial
de
camélidos sudamericanos
A) VVFF
B) FVFV
C) VFFV
D) FFVV
E) VFVF
#ESPECIALISTASUNI
SIMULACRO CEPRE UNI 2024-2
43. En
Egipto nació una de las
civilizaciones más importantes de la
Edad Antigua, sobre ella ordene
cronológicamente los eventos de su
desarrollo histórico:
I. Se recuperó el poder de Tebas luego
de expulsar a los hicsos.
II. Se desarrolló la primera unificación
del Alto y Bajo Egipto.
III. Se construyeron las pirámides de
Gizeh y la Esfinge.
IV. Se estableció el culto a Amón-Ra
como divinidad imperial.
A) II, III, IV, I
B) II, I, IV, III
C) II, I, III, IV
D) IV, I, III, II
E) III, II, I, IV
44. Con
respecto a las sociedades
desarrolladas en el periodo formativo y
el Intermedio. Temprano, marque la
alternativa que contiene afirmaciones
correctas.
I. Paracas en su fase cavernas tiene
tumbas rectangulares con un gran
número de momias.
II. El poder de Chavín se sustenta en el
conocimiento astronómico de sus
sacerdotes.
III. Nasca destacó en el desarrollo
cerámico, sobre todo con los huacos
eróticos.
IV. Moche destacó en orfebrería,
muestra de ello se encuentra en la
tumba del Señor de Sipán.
A) III y IV
B) I y III
C) I y II
D) II y III
E) II y IV
45. Las culturas Moche y Nazca fueron las
mas importantes del periodo de
Desarollos Regionales o intermedio
Temprano. Entre las características en
común de estas sociedades podemos
mencionar que
A) conformaron Estados de alcance
panandino.
B) alcanzaron un gran avance en.
cerámica.
C) produjeron los primeros centros
religiosos.
INFORMES: 993 750 351
GRUPO DE ESTUDIO NOSTRADAMUS
D)
fueron
contemporáneas
Tahuantinsuyo. al
E) se desarrollaron en la costa central.
GEOGRAFÍA
46. De las siguientes ciudades en el Perú,
¿cuál se ubica más al oriente?
A) Tumbes
B) Lima
C) Ica
D) Chiclayo
E) Puno
47. Marque la alternativa que relacione, de
modo correcto, a las líneas geodésicas
con los continentes que recorren.
I. Meridiano base
II. Trópico de Capricornio
III. Trópico de Cáncer
a. América del Sur
b. Europa
c. Asia
A) Ic, lla, llIb B) la, lIb, IIIc
C) Ib, IIc, Illa D) Ic, llb, IIIa
e) Ib, lIa; Illc
48. Desde el 2021 se estableció que los
cludadanos de los países como Perú,
Ecuador, Colombia y Bolivia pueden
ingresar, residir, trabajar y circular
libremente de modo temporal 0
permanente dentro de sus territorios.
Esto es posible porque sus Estados
han aceptado las condiciones del
A) Convenio de Ayuda Amazónica.
B) Tratado Comercial de Mercosur.
C) Estátuto Migratorio Andino.
D) Acuerdo del Pacto Andino.
E) Acta de Fundación de Unasur.
SIMULACRO CEPRE UNI 2024-2
50. En el departamento de Tumbes el
distrito de Aguas Verdes, colindante
con el país de Ecuador, es denominado
como _________de frontera.
A) una región
B) una zona
C) un área
D) un corredor
E) un entorno
51. Sobre la localización del Perú, indique
las proposiciones verdaderas.
I. La amazonia ocupa un amplio sector
de su territorio.
II. Se encuentra localizado en el
hemisferio septentrional.
III. Es un país de tipo marítimo, andino
y bioceánico.
IV. Se encuentra en dirección boreal de
la línea ecuatorial.
A) II y IV
B) II y III
C) III y IV
D) I y IV
E) I y III
52. En relación con la Organización del
Tradado de Cooperación Amazonica;
señale verdadero (V) o falso (F), según
corresponda
en
los
siguientes
enunciados en respectivo orden.
- Nació con la firma del acuerdo de
Cartagena.
- Promueve la inclusión social en la
región.
- La sede de la OTCA se encuentra
en Quito.
- Busca el desarrollo sostenible en la
región.
A) VFFV
B) FVFV
C) VFVF
D) VVFF
E) FFVF
49. El
domumento cartográfico más
adecuado donde se representa a la
plaza San Martin del Centro Histórico
de Lima y sus casas aledañas seria
A) un plano.
B) una carta.
C) un mapa.
D) un planisferio.
E) un mapa totográfico.
#ESPECIALISTASUNI
INFORMES: 993 750 351