Unidad Didáctica

Universidad de Costa Rica- Sede Occidente
Departamento de Ciencias Naturales
Enseñanza de las matemáticas
II semestre- 2021
Unidad Didáctica:
“Preparando FARO en matemáticas”
Autoras:
Tatiana Malespín Alvarado
Valeria María Rodríguez Castro
Alejandra María Solano Cruz
Unidad didáctica: “Preparando FARO en matemáticas”
El siguiente trabajo consta de una unidad didáctica para
la prueba FARO. En el documento se contemplan las
habilidades del plan de estudios del Ministerio de Educación
Pública (MEP), específicamente en cuanto a los contenidos
de Geometría Ánalítica, Relaciones y Álgebra y
Probabilidad y Estadística de Décimo año de la educación
diversificada costarricense.
La guía contiene ejercicios en forma variada, donde se
abordan ejemplos contextualizados y no contextualizados,
de esta manera el estudiante podrá mediante la
observación de ejemplos aplicados en la vida cotidiana
comprender de una mejor forma.
El principal objetivo es que sirva de recurso para los
estudiantes que deseen prepararse para dicha prueba.
Materiales requeridos:
❖ Un cuaderno, lápiz y borrador.
❖ Un dispositivo inteligente con
acceso a internet.
❖ Calculadora científica.
❖ Un lugar con iluminación.
Indicaciones:
❖ Es recomendable estudiar un
aproximado de 30 minutos
diarios.
❖ Avanzar con los temas de manera
cronológica y continuar con el
siguiente hasta comprender el
anterior.
❖ Realizar los ejercicios propuestos.
Tema 1. Geometría Análitica
En 1637 René Descartes matemático y filósofo
francés, publicó su obra La Géométrie, en la cual
introdujo un mecanismo para unir la Geometría con la
Aritmética, dos ramas de las matemáticas. La
característica básica de este nuevo proceso, ahora
llamado Geometría analítica, es el uso de un sistema
coordenado. Por medio de este nuevo sistema, los
métodos algebraicos se pueden aplicar al estudio de
la geometría. (Fuller y Tarwater, 1995, p.12)
Conceptos básicos
Plano cartesiano
Es una superficie de dos dimensiones formada por dos rectas numéricas. Una recta
es horizontal y se llama el eje “x” o abscisas. La otra recta numérica es vertical y se
llama el eje “y” u ordenadas. Como se observa en la siguiente gráfica:
Ubicación de puntos en el plano cartesiano
Para localizar un punto en
el plano cartesiano se toma
como referencia el
origen (0,0), a partir de él se
avanza tanto como lo
indique el primer número
(abscisa) hacia la derecha o
izquierda, según sea su
signo respectivamente, y a
partir de la nueva posición
se avanza hacia arriba o
abajo, según lo indique el
signo del segundo número
(ordenada). Ejemplo: Para localizar el punto A(3,2), nos movemos del centro del
plano cartesiano 3 unidades a la derecha en el eje “x”, ya que el número es
positivo, y luego subimos dos unidades en el eje “y”, pues el número es positivo.
De igual forma para localizar el punto B(-2,-1) nos movemos del centro 2 unidades
hacia la izquierda y 1 unidad hacia abajo.
Distancia entre dos puntos
Dados dos puntos cualesquiera 𝐴(𝑥 1, 𝑦1),
𝐵 (𝑥 2, 𝑦2), definimos la distancia entre ellos,
𝑑(𝐴, 𝐵 ), como la longitud del segmento que los
separa.
La fórmula de la distancia entre dos puntos, es la
siguiente:
Ejemplo: Dados los puntos 𝐴(3, 1) y
𝐵 (− 1, − 1), la distancia entre A y B la
calculamos sustituyendo en la fórmula:
Circunferencia
Una circunferencia es el conjunto de
puntos coplanares que son
equidistantes de un punto fijo llamado
centro, como se muestra en la figura
adjunta, donde O es el centro de la
circunferencia y A , B y C son tres
puntos pertenecientes a ella, entonces
OA= OB=OC.
Radio
Llamamos radio a la distancia del centro
de la circunferencia a un punto de la
misma. Por ejemplo, observando la
gráfica, observamos que O es el centro y
el segmento OC es un radio, donde su
valor es 1.
Diámetro
Un diámetro es todo segmento que
contiene al centro de la circunferencia
y está formado por dos radios, como
se aprecia en la figura, AC es el
diámetro de la circunferencia de centro O
y además AC=2OC.
Un pequeño incendio
En San Ramón centro,
alrededor de las 10 a.m se
empezó a percibir un olor a
humo, el cual era
proveniente de una soda
del Mercado Municipal. El
centro del problema tenía
como ubicación 100 metros
norte y 300 metros oeste
del Cuerpo de Bomberos.
Cuando ellos llegan al
lugar, piden la evacuación
de todas las personas a
una distancia mínima de
300 metros a la redonda.
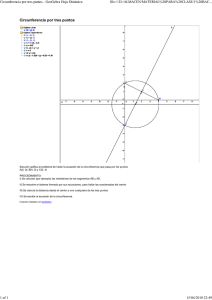
Tomando en cuenta la gráfica que muestra la ubicación de cada lugar, donde cada
unidad representan 100 metros, conteste lo siguiente:
1) ¿Cuánta distancia se debe recorrer del centro del accidente al hospital
(ubicado 500 metros norte y 300 metros oeste) si hubo algún herido?
2) Observando el radio de evacuación presente en la siguiente animación:
https://www.geogebra.org/classic/xdjrmnbq
Indique si los puntos marcados en el mapa Centro Médico Jackson 's
Memorial y el Banco Nacional deben ser evacuados?.
Habilidad 1: Representar gráficamente una circunferencia dado su
centro y su radio.
Ejemplo 1: Determine la gráfica de la circunferencia que tiene centro en 𝐶(− 4, 2) y
radio 𝑟 = 3.
Solución:
Ejemplo 2: Un barco salió muy temprano del muelle y después de unas horas
desean saber a qué distancia están de su punto de partida. El barco tiene un radar
con un alcance de 3km a la redonda, el cuál les indica que están ubicados a 2km
oeste y 3 km norte del muelle. Determine la representación gráfica que modela el
alcance máximo del radar tomando como centro la ubicación del barco.
Solución:
Habilidad 2: Representar algebraicamente una circunferencia dado su
centro y su radio.
Ecuación de la circunferencia
Inicialmente antes de conocer la ecuación de la circunferencia, se va a explicar
un poco de donde se origina, se sabe que el radio es la distancia 𝑑 del centro, a un
punto que se encuentra en la circunferencia , esa distancia puede ser calculada
con la fórmula de distancia entre dos puntos, la cual es:
Si se cambia 𝑑 por el radio (𝑟)
Y se eleva ambos lados al cuadrado para cancelar la raíz cuadrada del lado
derecho, de esta forma se obtiene la siguiente igualdad:
Ahora si se considera la circunferencia en el plano cartesiano para cualquier punto
perteneciente a ella con centro O(h,k) y radio r, se obtiene la ecuación de la
circunferencia:
donde el centro es el punto (ℎ, 𝑘) y el radio es 𝑟, se sustituyen para determinar la
ecuación de cualquier circunferencia cómo se muestra a continuación:
Centro: (2,-3)
Radio: 2
Ecuación:
Centro: (-2,1)
Radio: 3
Ecuación:
2
2
( 𝑥 − 2) + ( 𝑦 + 3) = 4
2
2
( 𝑥 + 2) + ( 𝑦 − 1) = 9
Ejemplo 1: Considere la siguiente gráfica, donde se ubica la circunferencia 𝐶 :
De acuerdo a la gráfica determine la representación algebraica de la circunferencia
.
2
2
2
La representación algebraica sustituyendo (𝑥 − ℎ) + (𝑦 − 𝑘) = 𝑟 sería:
Ejemplo 2: Una familia desea construir un encierro para gallinas de forma circular,
que tenga un radio de 2 metros. El centro de este encierro debe estar ubicado 4m
norte y 3m este de la casa. Determine la ecuación de la circunferencia de la
ubicación del encierro con respecto a la casa de la familia.
2
2
2
La representación algebraica sustituyendo (𝑥 − ℎ) + (𝑦 − 𝑘) = 𝑟 sería:
Habilidad 3: Aplicar traslaciones a una circunferencia.
Traslación de una circunferencia
La traslación se puede considerar como un cambio respecto a los ejes de
referencia pero sin la necesidad de girarlos, estos nuevos ejes son paralelos a los
originales.
Esta traslación se calcula con la fórmula:
2
( 𝑥 − ℎ − 𝑎)
2
+ (𝑦 − 𝑘 − 𝑏)
2
=𝑟
En donde (ℎ, 𝑘) son las coordenadas del centro original de la circunferencia, y 𝑟
el radio el cual se mantiene y (𝑎, 𝑏) la dirección a la cual se desea trasladar.
A continuación se presenta una imagen donde se observa una traslación de una
circunferencia con centro (2,1) y radio 2, trasladada en una dirección (-3,5).
Su ecuación original era
2
( 𝑥 − 2)
2
+ ( 𝑦 − 1)
= 4
Y usando la fórmula, la ecuación resultante es
2
( 𝑥 − 2 + 3)
2
+ ( 𝑦 − 1 − 5)
2
( 𝑥 + 1)
2
+ ( 𝑦 − 6)
= 4
= 4
Ejemplo 1: Considere la siguiente gráfica:
De acuerdo a la gráfica anterior, conteste las siguientes preguntas:
1. Si la circunferencia “𝐶1” se traslada desplazando su centro una unidad a la
izquierda (paralelo al eje x), y dos unidades hacia arriba (paralelo al eje y)
entonces se obtiene una circunferencia cuya ecuación corresponde a
2. Si la circunferencia “𝐶1” se traslada desplazando su centro dos unidades a la
derecha (paralelo al eje x) y una unidad hacia abajo (paralelo al eje y)
entonces se obtiene una circunferencia cuya ecuación corresponde a
Ejemplo 2:
Considere la siguiente
información:
Un ingeniero realiza un
esquema sobre la creación de
una granja avícola para la cría
de aves de corral tales como
pollos, pavos, patos, y gansos.
Cada corral está representado
en forma circular de 2 m de
diámetro. Todavía no decide
donde colocar los corrales, o si
quitar alguno, así que traslada
las circunferencias del
esquema para ir observando
cómo quedarán.
De acuerdo con la información anterior, considere las siguientes proposiciones:
I.
Para obtener 𝐶4se puede trasladar 𝐶2 cuatro unidades a la derecha.
II.
Para obtener 𝐶1se puede trasladar 𝐶3 una unidad hacia arriba.
III.
Para obtener 𝐶1se puede trasladar 𝐶4dos unidades hacia arriba y dos
unidades a la izquierda.
De ellas, ¿cuáles son verdaderas?
A)
B)
C)
D)
I y II
II y III
III y I
Todas
Habilidad 4: Resolver problemas relacionados con la circunferencia y
sus representaciones.
Ejemplo: Considere la siguiente información:
La siguiente figura está conformada por tres circunferencias, 𝐶1, 𝐶2 y 𝐶3, las cuales
coinciden en los centros B y D.
A-B-C-D-E
De acuerdo con la información anterior, considere las siguientes proposiciones:
I.
La medida del diámetro de 𝐶1 es el doble de la medida del diámetro de 𝐶2.
II.
III.
La distancia entre los puntos 𝐸𝐶 es igual a la distancia entre los puntos 𝐵𝐸.
La medida del radio de la circunferencia que contiene los puntos 𝐵 , 𝐶, 𝐷 es de
uno.
De ellas, ¿cuáles son verdaderas?
A)
B)
C)
D)
I y II
II y III
III y I
Todas
Habilidad 5: Determinar gráfica y algebraicamente si un punto se ubica
en el interior o en el exterior de una circunferencia.
Puntos con respecto a una circunferencia
En este apartado se abordará cómo podemos conocer la posición relativa de un
punto, con respecto a una circunferencia, para esto, considere una circunferencia
con centro (ℎ, 𝑘), radio 𝑟, y un punto con coordenadas (𝑥 , 𝑦).
Entonces podemos decir lo siguiente:
❖ Un punto es interior a la circunferencia
si: (𝑥 − ℎ)
2
2
+ ( 𝑦 − 𝑘) < 𝑟
2
❖ Un punto es exterior a la circunferencia
si: (𝑥 − ℎ)
2
2
+ ( 𝑦 − 𝑘) > 𝑟
2
❖ Un punto pertenece a una
circunferencia
si: (𝑥 − ℎ)
2
+ ( 𝑦 − 𝑘)
2
=𝑟
2
Ejemplo 1. Determine la posición relativa de los puntos (3, 2), (2,4) y (3,5) con
2
2
respecto a la circunferencia de ecuación (𝑥 − 2) + (𝑦 − 1) = 9.
Ejemplo 2. En la escuela de la comunidad Las Cascadas, colocaron internet de libre
acceso para que los estudiantes puedan estudiar desde sus casas, este funciona
por medio de una antena que tiene un alcance de 3km de radio, y se considera la
ubicación de la antena como el punto central de la señal, es decir (0,0). La maestra
les pide a sus alumnos la dirección de sus casas con respecto a esta antena, y así
conocer la situación de cada estudiante.
De acuerdo a la información anterior, ayude a la maestra a completar la siguiente
tabla con los datos de los estudiantes que ya han brindado la dirección, marque con
una “X” según corresponda:
Nombre
Ubicación
Ana
1km este y 2km sur
Juan
3 km sur
Lucrecia
½ km este y 2km
norte
María
2km norte y 3 km este
Recibe
señal
Está sobre el
límite de señal
No recibe
señal
Habilidad 6: Determinar si una recta dada es secante, tangente o
exterior a una circunferencia.
Habilidad 7: Representar gráfica y algebraicamente rectas secantes,
tangentes y exteriores a una circunferencia.
Rectas con respecto a una circunferencia
Una recta vertical tiene ecuación 𝑥 = 𝑐 y la horizontal 𝑦 = 𝑘, las que no son
horizontales ni verticales tienen ecuación 𝑦 = 𝑚𝑥 + 𝑏.
A continuación se observará un geogebra animado, donde podrá observar como
varían las rectas verticales y horizontales, de acuerdo a su valor.
Rectas horizontales y verticales – GeoGebra
Rectas con respecto a una circunferencia
Se debe recordar que la recta tiene ecuación 𝑦 = 𝑚𝑥 + 𝑏 y la circunferencia
2
2
2
𝑟 = (𝑥 − ℎ) + (𝑦 − 𝑘) , si se sustituye la ecuación de la recta en 𝑦 en la
2
ecuación de la circunferencia de esta manera 𝑟 = (𝑥 − ℎ)
2
+ (𝑚𝑥 + 𝑏 − 𝑘)
se obtiene una ecuación cuadrática y de ahí su discriminante denotado por ∆.
● Recta secante: Es la recta que corta dos puntos cualquiera, que
pertenecen a la circunferencia. Esto si ∆ > 0 ya que eso implica que la
ecuación tiene dos
soluciones reales.
● Recta tangente: Es la
recta que corta un
punto cualquiera que
pertenece a la
circunferencia, esta
recta es perpendicular
al radio, en el punto de
tangencia, es decir, el
ángulo que se forma entre el radio y la recta tangente es de 90°. Esto si
∆ = 0 ya que eso implica que la ecuación tiene una solución real.
2
● Recta exterior: Es la recta que no corta ningún punto perteneciente a la
circunferencia. Esto si ∆ < 0 ya que eso implica que la ecuación no tiene
soluciones reales.
Ejemplo 1. Considere la siguiente gráfica de la circunferencia 𝐶:
De acuerdo a la gráfica anterior, conteste las siguientes preguntas:
1. ¿Cuál de las siguientes rectas es tangente a 𝐶?
A) 𝑦 = 1
B) 𝑦 =
− 4
C) 𝑦 =
− 3
D) 𝑦 = 2
2. ¿Cuál de las siguientes rectas es secante a 𝐶?
A) 𝑥 =
− 1
B) 𝑥 =
− 3
C) 𝑥 = 4
D) 𝑥 = 2
Ejemplo 2. Considere la siguiente información:
2
2
Sea la circunferencia 𝐶, cuya ecuación está dada por 𝑥 + (𝑦 − 3) = 10
De acuerdo a la información anterior, considere las siguientes proposiciones:
I.
La recta 𝑥 = 4 es exterior a la circunferencia 𝐶
II.
La recta 𝑦 = 𝑥 es secante a la circunferencia 𝐶
III.
La recta 𝑦 = 3𝑥 + 13 es tangente a la circunferencia 𝐶
De ellas, ¿cuáles son verdaderas?
A) I y II
B) II y III
C) III y I
D) Todas
Ejemplo 3. Considere la siguiente información:
Para realizar un parque temático en la ciudad, elaboraron un esquema, donde las
circunferencias son las carpas que tendrá cada temática distinta, cómo se muestra
en el siguiente gráfico:
Considere las siguientes rectas, que serán utilizadas como caminos:
I.
La recta 𝑥 = 0 es secante a la circunferencia 𝐶4
II.
La recta 𝑦 =
III.
La recta 𝑥 = 4 es exterior a la circunferencia 𝐶1
− 1 es tangente a la circunferencia 𝐶 2
De ellas, ¿cuáles son verdaderas?
A)
B)
C)
D)
I y II
II y III
III y I
Todas
Habilidad 8. Analizar geométrica y algebraicamente la posición relativa
entre rectas en el plano desde el punto de vista del paralelismo y la
perpendicularidad.
Ecuación de una recta
La recta se puede representar en un plano cartesiano. Su notación algebraica
corresponde a la forma 𝑦 = 𝑚𝑥 + 𝑏, donde 𝑚 y 𝑏 son constantes reales y 𝑥 es una
variable real. La constante 𝑚 es la pendiente de la recta, y 𝑏 es el punto de corte de
la recta con el eje 𝑦 en (0, 𝑏). Si se modifica 𝑚, entonces se modifica la inclinación
de la recta. Como se aprecia en la siguiente animación:
https://www.geogebra.org/classic/nn2bddsn
Para determinar la ecuación de una recta debemos tomar en cuenta lo siguiente:
𝑦 = 𝑚𝑥 + 𝑏
Ecuación de la recta:
Pares ordenados:
(𝑥1, 𝑦1) y (𝑥2, 𝑦2)
𝑦2−𝑦1
Valor de la pendiente:
𝑚 =
Valor de 𝑏 :
𝑏 = 𝑦 − 𝑚𝑥
𝑥2−𝑥1
Haciendo uso de la calculadora según el modelo:
Modelo fx-Class Wiz
Modelo fx-ES PLUS
MENU A 1:2
MODE 5:1
Aparecerá una ventana de esta forma:
Aparecerá una ventana de esta forma:
Para formar el criterio
𝑦 = 𝑚𝑥 + 𝑏
𝑥 = 𝑚
y
𝑦 = 𝑏
Ejemplo: Para determinar la ecuación de la recta que pasa por los puntos (− 2, 5) y
(3, − 2), realizamos lo siguiente:
Tomamos en cuenta que nos debe quedar de la forma: 𝑦 = 𝑚𝑥 + 𝑏
Nuestros pares ordenados son:
(− 2, 5)y (3, − 2)
Haciendo uso de la calculadora apretamos las teclas MODE 5:1 ó MENU A:12, y
colocamos los pares ordenados de la siguiente forma:
Donde para colocar un par ordenado se coloca el número y se toca la tecla “=”, se
coloca la coma como un uno, y se toca la tecla “=” y se coloca el siguiente número y
se toca la tecla “=”, así sucesivamente con el otro par ordenado.
Para formar el criterio
𝑦 = 𝑚𝑥 + 𝑏
𝑥 = 𝑚
y
Entonces el valor de la pendiente es 𝑚
Y el valor de 𝑏
=
=
𝑦 = 𝑏
−
7
5
11
5
Por lo tanto la ecuación de la recta que pasa por los puntos (− 2, 5) y (3, − 2) es:
𝑦 =
−7
5
𝑥 +
11
5
Ejercicios:
1. Halle el criterio de la recta que pasa por (− 3, 5) y (7, − 15)
2. Halle el criterio de acuerdo con los datos de la gráfica:
3. Halle el criterio de acuerdo con los datos de la gráfica:
Rectas Paralelas
Dos rectas son paralelas si son
equidistantes, es decir nunca tendrán
alguna intersección.
De forma algebraica podemos ver que
sus pendientes son iguales. Es decir
dos rectas 𝑙1 y 𝑙2 con pendientes 𝑚1 y
𝑚2 son paralelas si 𝑚1 = 𝑚2
Ejemplo:
Sea 𝑙 = 2𝑥 + 1 y
1
𝑙2 = 2𝑥 − 3
↓
𝑚1 = 2
↓
𝑚2 = 2
como las pendientes son iguales, 𝑙 y
1
𝑙2 son rectas paralelas.
Rectas Perpendiculares:
Dos rectas son perpendiculares cuando
su intersección forma un ángulo recto
(90°), como se muestra en el gráfico.
De forma algebraica podemos ver que el
producto de sus pendientes da como
resultado -1. Es decir dos rectas 𝑙1 y 𝑙2
con pendientes 𝑚1 y 𝑚2 respectivamente
son perpendiculares si y solo si
𝑚1 · 𝑚2 = − 1 en forma simbólica se
obtiene 𝑙1 ⊥ 𝑙2 .
Ejemplo:
Sea 𝑙
=
1
𝑙2 =
−4
3
3
4
𝑥 + 2y
𝑥 + 1;
𝑚1 · 𝑚2 =
3
4
·
−4
3
=
− 1
Ejemplo. Considere la siguiente información
Un arquitecto realiza un bosquejo para la creación de un parque que debe tener
diferentes caminos para conectar las secciones en las que se dividirá. Los caminos
están numerados como se muestra en la siguiente imagen:
De acuerdo con la información anterior, considere las siguientes proposiciones:
I.
Los caminos 1 y 2 son perpendiculares entre sí.
II.
Los caminos 5 y 4 son paralelos entre sí.
III.
Los caminos 1 y 3 son perpendiculares entre sí.
De ellas, ¿cuáles son verdaderas?
A)
B)
C)
D)
I y II
II y III
III y I
Todas
Habilidad 9. Aplicar la propiedad que establece que una recta tangente
a una circunferencia es perpendicular al radio de la circunferencia en el
punto de tangencia.
Propiedad de recta tangente a una circunferencia
Una recta es tangente a una circunferencia si, y sólo si, es perpendicular a su
radio. Es decir, si una recta 𝐴𝑁 es tangente en el punto 𝑁 ⇒ ∠ 𝑂𝑁𝐴 = 90°,ángulo
formado por la intersección perpendicular entre la recta y el radio. Como se
observa en el siguiente gráfico:
Algunas observaciones:
● El punto de contacto entre una circunferencia y una recta, se denomina
punto de tangencia.
● El radio de una circunferencia y un punto de esta, forman un único punto de
tangencia.
● El ángulo de 90° también se denomina ángulo recto.
El siguiente link nos llevará a una animación con GeoGebra para esta habilidad :
https://www.geogebra.org/classic/jjxqxmmq
Ejemplo. Considere la siguiente gráfica donde 𝑙 es una recta y el punto A es
tangente a la circunferencia de centro O:
Según la gráfica anterior, determine la medida del segmento 𝐴𝐵
Habilidad 10. Determinar la medida de perímetros y áreas de
polígonos en diferentes contextos
Polígonos
Polígono regular
Los polígonos regulares son polígonos equiláteros, puesto que todos sus lados
son de la misma longitud.
Elementos de un polígono regular
➢ Lado: Son los segmentos congruentes entre sí que conforman el polígono.
➢ Centro: Es el punto que se
encuentra a igual distancia de
todos los vértices.
➢ Vértice: Es el punto donde
coinciden dos lados consecutivos.
➢ Radio: Es el segmento que une
el centro del polígono con sus
vértices.
➢ Apotema: Es el segmento que
cae perpendicularmente sobre un
lado del polígono desde el centro.
Polígonos especiales
Ejemplo. Analice la siguiente figura:
De acuerdo a la figura anterior, conteste las siguientes preguntas:
1. ¿Cuál es el área del triángulo DBC?
A) 12
B) 9
C)
9 3
2
D) 3 3
2. ¿Cuál es el perímetro del polígono GABCDEF?
A) 27
B) 9
C) 21
D) 20
Habilidad 11. Determinar las medidas de los ángulos internos y
externos de polígonos en diversos contextos.
Ángulos de un polígono regular
Ángulo central: Es el ángulo formado por los
radios que unen dos vértices consecutivos de
un polígono con vértice en el centro.
Ángulo interno: Es el ángulo formado por dos
lados consecutivos de un polígono.
Ángulo externo: Es el ángulo suplementario
del ángulo interno.
Ejemplo. Analice la siguiente imagen:
De acuerdo a la imagen anterior, conteste las siguientes preguntas:
1.
¿Cuál es la medida del ángulo ∡CBA ?
A) 120°
B) 90°
C) 30°
D) 60°
2. ¿Cuál es la medida del ángulo ∡ABE?
A) 60°
B) 20°
C) 30°
D) 120°
Habilidad 12. Determinar la medida del apotema y el radio de
polígonos regulares y aplicarlo en diferentes contextos.
Apotema y radio en polígonos regulares
Recordemos que lo siguiente:
➢ Radio: Es el segmento que une el centro del polígono con sus vértices.
➢ Apotema: Es el segmento que cae perpendicular a un lado del polígono
desde el centro.
Para calcular el radio y apotema de un polígono regular podemos realizarlo
sabiendo el número de lados del polígono y la medida de cada lado.Por medio de
la tangente de la mitad del ángulo central y un lado, podemos determinar el
apotema del polígono regular.
Notemos
Para calcular el apotema para cualquier polígono regular solamente tenemos que
saber el número de lados del polígono y uno de sus lados.
Ejemplo:
Si la medida del lado de un pentágono regular es 3 cm, determine la medida del
apotema.
Ejemplo. Si la medida del lado de un triángulo equilátero (polígono regular) es 10
cm. Determine la medida de su radio.
Otra forma para determinar la medida del apotema y el radio de polígonos
regulares en diferentes contextos para casos especiales es utilizando el uso de sus
distintas fórmulas para cada polígono regular especial.
Anteriormente se habían visto las fórmulas para el área y el perímetro, ahora se
verán las fórmulas para calcular su apotema y su radio:
Triángulo equilátero
Lado: 𝑙
Altura:ℎ
Apotema:
Radio:
Cuadrado
Lado: 𝑙
Altura:ℎ
Apotema:
Radio:
Hexágono
Lado: 𝑙
Altura:ℎ
El lado y el radio
de un hexágono son iguales
Apotema:
Radio:
Ejemplo
Un arqueólogo fue a Egipto para
analizar la pirámide de Keops, que
tiene una estructura de un triángulo
equilátero, donde uno de sus lados
mide 230 m y con una altura
aproximada de 138 m como se
observa en la figura.
De acuerdo al contexto anterior, determine el apotema y el radio de la pirámide.
Habilidad 13. Estimar perímetros y áreas de figuras planas no
poligonales utilizando un sistema de coordenadas rectangulares.
Polígonos irregulares
Para determinar estimaciones de áreas o perímetros de figuras no regulares la
debemos descomponer en figuras conocidas como triángulos, cuadrados, etc.
Ejemplo. Considere la siguiente imagen:
De acuerdo a la imagen anterior, ¿Cómo podríamos realizar la estimación del área
del polígono irregular?
Habilidad 14. Resolver problemas que involucren polígonos y sus
diversos elementos.
Ejemplo 1:
Una costurera desea realizar el cobertor de una almohada en forma de cuadrado
regular donde sus lados miden 30 cm. Determine el radio, apotema, perímetro y
área de la tela resultante.
Ejemplo 2:
Un hijo le muestra a su mamá un lego en forma de polígono regular y le pide que
analice dos proposiciones sobre un polígono regular. El polígono que se mostró a la
madre es el siguiente:
Las proposiciones del hijo son las siguientes:
I.
La medida del radio es mayor que la medida del apotema.
II.
La medida de un ángulo central es la misma que la de un ángulo externo.
De las anteriores,¿cuál o cuáles son afirmaciones verdaderas del hijo?
A) Solo la I
B) Sola la II
C) Ambas
D) Ninguna
Habilidad 15. Determinar ejes de simetría en figuras simétricas
Ejes de simetría
Un eje de simetría es una línea imaginaria que al dividir una figura cualquiera, lo
hace en dos partes, y cuyos puntos simétricos son equidistantes a dicho eje. Como
podemos ver en la siguiente figura:
Todos los polígonos regulares son figuras simétricas y pueden tener más de un eje
de simetría, por ejemplo las siguiente figuras:
Ejemplo. A continuación se presentan dos columnas: A y B. En la columna A se
ubican diferentes figuras simétricas. En la columna B, el número de ejes de simetría
que contienen. Haga corresponder cada uno de los elementos de la columna A con
la columna B, escribiendo la letra correspondiente dentro del paréntesis.
Columna A
Columna B
A)
( ) Un eje de simetría
B)
( ) Dos ejes de simetría
C)
( ) Tres ejes de simetría
D)
( ) Cuatro ejes de simetría
Habilidad 16. Identificar elementos homólogos en figuras que presentan
simetría axial.
Habilidad 17. Resolver problemas relacionados con la simetría axial.
Simetría axial
La simetría axial, es un concepto que se trabaja en el plano cartesiano, decimos
que una figura plana tiene simetría axial cuando podemos trazar una recta (llamada
eje de simetría) que divide en dos partes la figura, de manera que si plegamos el
plano por ese eje las dos partes coinciden.
Observaciones:
● El eje de simetría funciona de la misma forma en la que se había visto
anteriormente, es decir los puntos homólogos deben ser equidistantes al eje,
sólo que está vez vamos a pasar este concepto al plano cartesiano.
● En la simetría axial se toman los ejes de simetría como una recta en “x” o “y”.
● Podemos utilizar el eje de simetría para encontrar ángulos homólogos,
vértices homólogos y lados homólogos de una figura.
Puntos o vértices homólogos: Con la simetría axial, las figuras simétricas
disponen de puntos homólogos: el punto A de una figura es homólogo al punto A’
(A prima), estos puntos son equidistantes al eje de simetría.
Lados homólogos: Podemos notar en la siguiente imagen que al igual que los
puntos homólogos, también están los lados, estos son los que al doblar el plano en
el eje de simetría dado, nos quedarán unos sobre otros.
Ejes de simetría en el plano cartesiano: Como se había mencionado
anteriormente, la simetría la podemos encontrar en el plano cartesiano, donde los
ejes de simetría son rectas con respecto al eje “x” o eje “y”. Como podemos apreciar
en la siguiente gráfica:
.
Ángulos homólogos: En esta otra gráfica podemos observar los ángulos
homólogos, y notamos que actúan de la misma forma que los puntos homólogos,
sólo que esta vez nos referimos a su ángulos.
Ejemplo 1 . Considere la siguiente gráfica:
De acuerdo a la gráfica anterior, considere las siguientes proposiciones:
I.
El eje de simetría que permite que 𝐴𝐵 sea homólogo a 𝐿𝐾 es 𝑦 = 3.
II.
Si el eje de simetría es 𝑥 = 3, 𝐹, es un punto homólogo a 𝐺.
De ellas, ¿cuál o cuáles son verdaderas?
A) Solo la I
C) Ambas
B) Solo la II
D) Ninguna
Ejemplo. Considere la siguiente gráfica
De acuerdo a la gráfica anterior, considere las siguientes proposiciones:
I.
La recta 𝑥 = 4, es un eje de simetría de la figura.
II.
𝐵𝐶 es homólogo con 𝐹𝐸 dado el eje de simetría 𝑦 = 3.
III.
∠𝐷𝐴𝐵 es homólogo con ∠𝐻𝐺𝐹 dado el eje de simetría 𝑥 = 5.
De ellas, ¿cuáles son verdaderas?
A) La I y II
B) La ll y lll
C) Ninguna
D) Todas
Habilidad 18. Aplicar el concepto de traslación, homotecia, reflexión y
rotación para determinar qué figuras se obtienen a partir de figuras
dadas.
Transformaciones en el plano
Una transformación en el plano o movimiento en el plano, es una función que hace
corresponder a cada punto del plano, otro punto del mismo plano, al cual se le llama
imagen. En general, una transformación es una operación geométrica que permite
encontrar o construir una nueva figura a partir de una que se ha dado inicialmente.
La nueva figura se llama homóloga o transformada de la original.
Las transformaciones se clasifican según las propiedades que conservan. Hay dos
clases:
Transformaciones Isométricas: Son aquellas que en el proceso de transformación,
sólo cambian la posición en la que se encuentran, pero conservan su tamaño
original. Estas transformaciones suelen llamarse movimientos en el plano. La figura
a la que se le aplica este tipo de transformación tiene como transformada, otra que
es congruente a ella. Corresponden a este tipo de transformaciones, la reflexión, la
traslación y la rotación.
Transformaciones Isomórficas: Son aquellas que en el proceso de transformación
pueden cambiar el tamaño según una razón de proporcionalidad entre las medidas
de las figuras involucradas.Entre estas transformaciones está la homotecia.
Traslación
Si existe una figura geométrica en el plano cartesiano, definiremos la traslación
como la cantidad de unidades que se moverá por medio de un vector 𝑇(𝑎, 𝑏), en
donde "𝑎" nos indicará la cantidad de espacios que se mueve horizontalmente, si
𝑎 > 0 se mueve hacia la derecha y si 𝑎 < 0 se mueve hacia la izquierda. Por otro
lado, "𝑏" nos indicará la cantidad de espacios que se mueve verticalmente, si 𝑏 > 0
se mueve hacia arriba y si 𝑏 < 0 se mueve hacia abajo.
Entonces, si tenemos un punto 𝐴 de coordenadas (𝑥 , 𝑦) y se desea aplicar la
traslación 𝑇(𝑎, 𝑏), el nuevo punto 𝐴' nos quedará como (𝑥 + 𝑎, 𝑦 + 𝑏).
Ejemplo. Si tenemos un triángulo de vértices (1, 1), (2, 3) y (3, 1) y le realizamos
una traslación de 5 unidades a la derecha y una unidad hacia abajo, realizamos lo
siguiente:
● (1, 1) nos queda (1 + 5, 1 − 1)=(6, 0)
● (2, 3) nos queda (2 + 5, 3 − 1)=(7, 2)
● (3, 1) nos queda (3 + 5, 1 − 1)= (8, 0)
El nuevo triángulo tendrá los vértices (6, 0), (7, 2), (8, 0)
Como se aprecia en la siguiente imagen:
Reflexión
La reflexión consiste en reflejar una figura con respecto a un eje de simetría. En
una reflexión cada punto de la figura inicial y su imagen están a la misma distancia
del eje de reflexión, el eje funciona como un espejo, las figuras se miran dándose
la espalda o mirándose de frente equidistantes del eje.
Ejemplo. Si tenemos un triángulo de vértices (4,4), (4,3), (4,2) y se ve reflejado con
respecto al eje de simetría 𝑥 = 6, para encontrar el triángulo formado por la reflexión
debemos contar los espacios que tiene cada punto con respecto al eje de simetría, y
esa va a ser la distancia que van a tener las nuevas coordenadas también al eje.
Veámoslo en la siguiente imagen:
● El punto (4,4) tiene una distancia de 2 unidades con respecto al eje x=6, así
que moviéndonos dos unidades después de 6 obtenemos (8,4).
● El punto (3,3) tiene una distancia de 3 unidades con respecto al eje x=6, así
que moviéndonos tres unidades después de 6 obtenemos (9,4).
● El punto (4,2) tiene una distancia de 2 unidades con respecto al eje x=6, así
que moviéndonos dos unidades después de 6 obtenemos (8,2).
Reflexión con respecto al eje X (Abscisas): La imagen de un punto 𝑃(𝑥 , 𝑦) que se
refleja con respecto al eje X, corresponde a 𝑃'(𝑥, − 𝑦).
Reflexión con respecto al eje Y (Ordenadas): Si la reflexión se realiza con
respecto al eje Y (Ordenadas) la imagen de 𝑃 resulta 𝑃'(− 𝑥, 𝑦).
Reflexión con respecto al eje origen (0,0) (
𝑦= 𝑥 ,
𝑦=
− 𝑥)
En el plano cartesiano la imagen de un punto 𝑃(𝑥, 𝑦) que se refleja con respecto al
origen, es 𝑃' (− 𝑥 , − 𝑦).
Rotación: La rotación es una transformación en el plano que consiste en girar
todos los puntos de un figura en torno a un punto 𝑂 fijo llamado centro de rotación,
tal que cada punto gira en una medida angular α llamado tal que cada punto gira
siguiendo un arco de circunferencia que tiene como centro 𝑂 y un ángulo α.
Si el ángulo de rotación es positivo, el giro se realiza en sentido antihorario y si el
ángulo de rotación es negativo, el giro se realiza en sentido horario.
Rotación con respecto al eje origen (0,0) en 90°
Observe la siguiente animación en Geogebra:
https://www.geogebra.org/classic/qcmkm9te
Rotación en sentido antihorario:
Rotación en sentido horario:
Homotecia
Es una transformación en la que a cada punto (𝐴, 𝐵 ) se le hace corresponder otro
(A’, B’) de tal forma que ambos están alineados con otro fijo 𝑂, llamado centro de
homotecia y donde se verifica que
𝑂𝐴'
𝑂𝐴
= 𝐾 siendo 𝐾 la razón de la homotecia.
Observe la siguiente animación en Geogebra.
https://www.geogebra.org/classic/kfwh52yg
Homotecia directa
Cuando la razón es positiva, la homotecia es directa y los puntos homotéticos están
situados a un mismo lado del centro O.
Homotecia inversa
Cuando la razón es negativa, la homotecia es inversa y los puntos homotéticos
están situados a ambos lados del centro O.
Ejemplo. Considere la siguiente gráfica
Ejemplo. Considere la siguiente información:
De acuerdo a la gráfica anterior conteste las siguientes preguntas:
1. Si se le aplica una única transformación al triángulo #1 y se obtiene el triángulo
#3, entonces esa transformación se denomina
A) rotación
B) reflexión
C) traslación
D) homotecia
2. Si se le aplica una única transformación al triángulo #1 y se obtiene el triángulo
#4, entonces, esa transformación consiste en aplicar una
A) reflexión sobre 𝑦 = − 𝑥
B) homotecia con centro en el origen de coordenadas
C) traslación de 2 unidades hacia abajo paralelo al eje y
D) rotación de 90° centrado en el origen de coordenada y sentido antihorario
3. Si el triángulo #3es el resultado de aplicar una única transformación al triángulo
#2,entonces el punto imagen de (1, 2) corresponde a
A) (1, 0)
B) (3, 0)
C) (1, − 1)
D) (3,-1)
Tema 2. Relaciones y funciones
En Mesopotamia los Babilonios
empezaron a desarrollar el álgebra con
ecuaciones, se conservan documentos,
que son tablillas de arcilla, donde se
imprimía el texto. Los problemas
algebraicos expresados eran
formulados y resueltos de una forma
verbal, sin emplear símbolos
especiales. Muchas veces aparecen palabras como longitud, anchura para
representar incógnitas pero no porque esas incógnitas representarán esas
cantidades, sino porque los problemas surgían de situaciones geométricas, sin
embargo cierta terminología terminó imponiéndose. (Lorente, S.F, p.7)
Conceptos básicos
Solución de una ecuación lineal: Para este tema es importante recordar como se
soluciona una ecuación lineal, veamos un ejemplo para recordarlo:
La motocicleta de Juan
Juan es un joven de 17 años que sueña con tener una motocicleta, para lo cual ha
ido ahorrando y tiene ₡170.000 colones, sin embargo en total necesita ₡350.000
colones, por lo cual ha iniciado un emprendimiento de lavar carros, y cobra ₡5000
colones por cada uno, por semana tiene una ganancia de ₡30.000 colones.
A partir de la situación anterior conteste las siguientes preguntas:
1. Determine la expresión algebraica que modela la cantidad de dinero que va
recaudando Juan en función de las semanas trabajadas.
2. Determine cuántas semanas debe trabajar Juan para obtener el dinero que
necesita. (Preimagen)
3. Grafique dicha situación en un sistema de ejes cartesianos.(Gráfica)
Habilidad 1. Identificar si una relación dada en forma tabular, simbólica
o gráfica corresponde a una función.
Funciones
Relación
Una relación es la correspondencia entre los elementos de dos conjuntos distintos
que conforman pares ordenados, una expresión que une dos o más elementos
entre sí conforma una relación.
Ejemplo
Ahora se va a relacionar los animales con su forma o formas de moverse.
Como se pudo observar anteriormente las relaciones de forma de movilizarse son:
➢ Caballo: camina
➢ Elefante: camina
➢ Pez: nada
➢ Tiburón: nada
Función
Una función es una relación
entre un conjunto nombrado
codominio (y= f(x)) y otro
llamado dominio (X) de
manera que a cada
elemento del dominio X se le
asigna un único elemento
del codominio f(x).
Esta relación queda más
clara con un Diagrama de
Venn
Es importante considerar que varios elementos del dominio(X) pueden estar
relacionados a un mismo elemento del codominio(Y), sin embargo un elemento del
dominio no puede estar relacionado a varios elementos del codominio.
Elementos de una función
★ Dominio: son los valores que se le asignan a la variable independiente y
sobre donde está definida la función, se le llama también conjunto de
partida y corresponden a las preimágenes. (𝐷𝑓). Para encontrar el dominio
se observa los puntos de la gráfica sobre el eje x para así encontrar el
conjunto. Se lee de izquierda a derecha.
★ Codominio: corresponden a las imágenes de la función.(𝐶𝑓)
★ Ámbito o Rango: corresponde al conjunto de imágenes que responden al
criterio de la función. (𝐴𝑓). Para encontrar el ámbito se observa los puntos
de la gráfica sobre el eje y para así encontrar el conjunto. Se lee de arriba a
abajo.
★ Criterio: corresponde a la expresión 𝑦 = 𝑓(𝑥 ).
Ejemplos:
1. Considere las siguientes representaciones gráficas
I
II
III
IV
¿Cuál o cuáles gráficas representan una función?
A) I y IV
B) III y II
C) I y II
D) III y IV
2. Considere las siguientes representaciones tabulares
I
X
1
2
3
2
Y
0
4
1
5
II
¿Cuál o cuáles de ellas representan una función?
A) Ambas
B) Ninguna
C) Sola la I
D) Solo la II
X
0
1
4
3
Y
2
2
7
1
3. Considere las siguientes relaciones
I.
ℎ: 𝑍 → 𝑍, 𝑐𝑜𝑛 ℎ(𝑥 ) = 𝑥
II.
𝑔: 𝑍
+
2
+ 9
→ 𝑍, 𝑐𝑜𝑛 𝑔(𝑥 ) = 𝑥 + 5
De las anteriores, ¿cuales corresponden a una función?
A) Ambas
B) Ninguna
D) Sola la I
C) Solo la II
4. Considere las siguientes representaciones gráficas:
De ellas, ¿Cuál o cuáles corresponden a una función?
A) Solo la 1
C) Ambas
B) Solo la 2
D) Ninguna
Habilidad 2. Evaluar el valor de una función dada en forma gráfica o
algebraica, en distintos puntos de su dominio.
Cálculo de Imágenes y Preimágenes
Imágen: en este caso se debe sustituir el elemento a en el criterio de la función
para así obtener su imágen f(a).
Preimagen: en este caso se debe igualar el elemento del codominio al criterio de
la función para así encontrar su preimagen.
Ejemplo
Considere la información de la siguiente figura que presenta la gráfica de una
función
De acuerdo a la imagen anterior, conteste las siguientes preguntas:
1. El valor de 𝑓(− 1) corresponde a
A) -1
B) -1.5
C) -2
D) 2
2. La preimagen de 0 corresponde a
A) -1
B) 0
C) 2
D) 1
Ejemplos:
1. La imagen de 2 en la función h dada por ℎ(𝑥 ) =
𝑥
3
+ 5
A) 12
B) 13
C) -1
D) 5
5
2. La preimagen de -3 en la función g dada por 𝑔(𝑥) = 2 + 4 𝑥
A) -4
B) 5
−7
C) 4
D) -3
Considere el siguiente gráfico para contestar las preguntas 3 y 4
3. ¿ Cuál es el valor de 𝑓(2)?
A) -1
B) 0
C) 2
D) 1
4. ¿ Cuáles son las preimágenes de 1?
A) -1 y -1
B) 0 y 1
C) 2 y 0
D) 1 y 2
Habilidad 3. Analizar una función a partir de sus representaciones.
Intervalos de monotonía
Creciente: una función f es creciente en un
intervalo, si cumple que para cualquier 𝑥 1, 𝑥 2,
que pertenecen al intervalo, tal que si 𝑥 1 < 𝑥 2
eso implica que 𝑓(𝑥 1) ≤ 𝑓(𝑥 2).
Decreciente: una función f es decreciente en un
intervalo, si cumple que para cualquier 𝑥 1, 𝑥 2, que
pertenecen al intervalo, tal que si 𝑥 1 < 𝑥 2 eso
implica que 𝑓(𝑥 1) ≥ 𝑓(𝑥 2).
Constante: una función f es constante en
un intervalo, si cumple que para cualquier
𝑥 1, 𝑥 2, que pertenecen al intervalo,
𝑓(𝑥 1) = 𝑓(𝑥 2).
Intersección con los ejes
Eje x: interseca en todos los puntos (x,0)
tal que f(x) = 0, en este caso lo que se
debe hacer es igualar el criterio a 0.
Eje y: interseca en todos los puntos (0,y)
tal que y = f(0), en este caso se sustituye
en el criterio.
Ejemplo
Considere la siguiente representación gráfica
1. De acuerdo con la información anterior, un intervalo en el cual el
comportamiento de la función es creciente corresponde a
A) ]-∞,4]
B) ]-2,0[ ∪ ]2,4[
C) ]-2,4[
D) [2,4]
2. De acuerdo con la información anterior, un intervalo en el cual el
comportamiento de la función es decreciente corresponde a
A) ]-∞,-2[ ∪]4,8]
B) ]-∞,-2[ ∪]4,8[
C) ]-∞,8[
D) ]-4,-2[ ∪]4,8]
Dominio y ámbito
Se debe recordar que anteriormente se estudió estos conceptos.
En el ámbito se consideran los puntos sobre el eje “y” y se lee de abajo hacia
arriba.
En el dominio se consideran los puntos sobre el eje “x” y se lee de izquierda a
derecha.
Ejemplo
Considere la siguiente representación gráfica
1. De acuerdo con la información anterior, el dominio de la función es.
A) ]-∞,4]
B) [-6,4]
C) ]-6,4[
D) [-6,+ ∞[
2. De acuerdo con la información anterior, el ámbito de la función es
A) [0,6]
B) ]0,6[
C) ]-6,4
D) ]4,8]
Habilidad 4. Calcular la composición de dos funciones.
Composición de funciones
Se describe la composición de funciones 𝑓: 𝐴 → 𝐸 y 𝑔: 𝐶 → 𝐵 denotado por 𝑔 ◦ 𝑓
a la función 𝑔 ◦ 𝑓: 𝐴 → 𝐵 , (𝑔 ◦ 𝑓)(𝑥 ) = 𝑔(𝑓(𝑥 )).
Ejemplo:
Consideremos las siguientes funciones
𝑓(𝑥) =
1
𝑥+2
𝑔(𝑥) =
𝑥
𝑥+1
definidas en su dominio máximo. Encuentre las funciones 𝑓
¿Será conmutativa la composición de funciones?
∘ 𝑔 y 𝑔 ∘ 𝑓.
Observación:
En general las funciones 𝑓 ◦ 𝑔 y 𝑔 ◦ 𝑓 no siempre son conmutativas.
Ejemplo:
Consideremos las siguientes funciones
𝑓(𝑥) =
𝑥+1
3
2
𝑔(𝑥) = 𝑥
definidas en su dominio máximo. Determine la composición
(𝑔 ∘ 𝑓 ) ( − 2 ).
Habilidad 5. Representar gráficamente una función lineal.
Función Lineal
Es una función de la forma
𝑦 = 𝑚𝑥 + 𝑏donde "𝑚"denota la
pendiente, la cual se calcula con la
fórmula 𝑚 =
𝑦 −𝑦1
2
𝑥2−𝑥1
, y "𝑏"corresponde
la intersección con el eje 𝑦 en (0, 𝑏).
Monotonía de la función:
Si 𝑚 = 0 es una función constante
Si 𝑚 < 0 es una función decreciente
Si 𝑚 > 0 es una función creciente
Ejemplo:
Observe la siguientes funciones lineales en un plano cartesiano
𝑓: ℝ → ℝ, 𝑓(𝑥) =
− 2𝑥y 𝑔: ℝ → ℝ, 𝑔(𝑥) =
https://www.geogebra.org/classic/pp9sakvu
Observaciones:
Si 𝑚 = 0 es una función constante.
Si 𝑚 < 0 es una función decreciente.
Si 𝑚 > 0 es una función creciente.
A continuación se le presentará un
link donde podrá ingresar a una
−
1
2
𝑥
animación, respecto a la función lineal, para visualizar los cambios en la gráfica al
modificar los valores de m y b.
https://www.geogebra.org/m/YxHkgqeB
Habilidad 6. Determinar la ecuación de una recta utilizando datos
relacionados con ella.
Recordemos que:
Para determinar la ecuación de una recta debemos tomar en cuenta lo siguiente:
𝑦 = 𝑚𝑥 + 𝑏
Ecuación de la recta:
Pares ordenados:
(𝑥1, 𝑦1) y (𝑥2, 𝑦2)
𝑦2−𝑦1
Valor de la pendiente:
𝑚 =
Valor de 𝑏 :
𝑏 = 𝑦 − 𝑚𝑥
𝑥2−𝑥1
Haciendo uso de la calculadora según el modelo:
Modelo fx-Class Wiz
Modelo fx-ES PLUS
MENU A 1:2
MODE 5:1
Aparecerá una ventana de esta forma:
Aparecerá una ventana de esta forma:
Para formar el criterio
𝑦 = 𝑚𝑥 + 𝑏
𝑥 = 𝑚
Ejemplo:
y
𝑦 = 𝑏
Determine la ecuación de la recta que contiene a los puntos A(-1,4) y B(3,6).
Habilidad 7. Analizar gráfica y algebraicamente la función cuadrática
con criterio 𝑓(𝑥) = 𝑎𝑥
2
+ 𝑏𝑥 + 𝑐, a ≠ 0.
Función cuadrática
Es una función de la forma
2
𝑓 ( 𝑥 ) = 𝑎𝑥
+ 𝑏𝑥 + 𝑐 , "𝑎" brinda
información sobre la concavidad de la
función si 𝑎 > 0 es cóncava hacia
arriba, y si 𝑎 < 0 es cóncava hacia
abajo.
Intersecciones con los ejes
El discriminante determina el número
de intersecciones con el eje x, su
fórmula es ∆ = 𝑏
2
− 4𝑎𝑐 , Si ∆ > 0
intersecta en dos puntos, ∆ = 0 interseca en un punto, ∆ < 0 no interseca en
ningún punto. Y estás intersecciones son las soluciones de dicha ecuación.
Y el punto (0, 𝑐) representa la intersección con el eje y.
Vértice
Se calcula con la fórmula 𝑉 = (
−𝑏
2𝑎
,
−∆
4𝑎
), representa el punto máximo o mínimo de
la función. Si 𝑎 > 0 es el vértice es punto mínimo y si 𝑎 < 0 el vértice es el punto
máximo. La coordenada 𝑥 =
Intervalos de monotonía
−𝑏
2𝑎
representa el eje de la simetría.
Para determinar los intervalos de monotonía de una función cuadrática, hay que
calcular
−𝑏
2𝑎
y la concavidad, y para determinar el ámbito hay que calcular
concavidad.
Ejemplo:
2
Consideremos la siguiente función 𝑥 + 5𝑥 + 6.
Determine la concavidad, vértices y las intersecciones con eje x y y.
−∆
4𝑎
y la
A continuación se le presentará un link donde podrá ingresar a una animación,
respecto a la función cuadrática, que le permitirá visualizar los cambios que sufre la
gráfica al modificar los valores de a, b y c.
https://www.geogebra.org/m/jVKqWYFy
Habilidad 8. Relacionar la representación gráfica con la algebraica.
Ejemplo. Considere la siguiente información:
Sea 𝑓 una función dada por 𝑓(𝑥 ) =
2
− 𝑥 + 3𝑥 , con ∆ > 0.
Considere las siguientes proposiciones:
I.
La gráfica de 𝑓 es cóncava hacia arriba.
II.
La gráfica de 𝑓 tiene dos intersecciones con el eje x.
De acuerdo con las afirmaciones anteriores, ¿cuál o cuáles son verdaderas de
acuerdo con la función de 𝑓 ?
A) Solo l
B) Solo ll
C) Ambas
D) Ninguna
Habilidad 9. Plantear y resolver problemas en contextos reales
utilizando las funciones estudiadas.
Ejemplo 1.
Considere el siguiente contexto:
Si el coste de fabricación de una blusa es de 2000 colones por unidad y lo
venden en el por 3000 colones.
De acuerdo con la información anterior, considere las siguientes proposiciones:
I.
La función de utilidades por cada blusa vendida es de forma
𝑓(𝑥 ) = 1000 𝑥 𝑠𝑖 𝑥 > 0.
II.
Si vendemos 15 blusas obtenemos una utilidad de 12000.
De acuerdo con las proposiciones, ¿cuál o cuáles son verdaderas?
A) Solo l
B) Solo ll
C) Ambas
D) Ninguna
Ejemplo 2. Consideremos la siguiente información:
En un partido de voleibol, un jugador logró pegarle a la pelota. Su trayectoria está
dada por la ecuación ℎ (𝑥 ) =
− 0. 0241 𝑥 ² + 𝑥 + 5. 5 , donde "ℎ " es la altura,
en metros, que alcanzó la pelota y “x” es la distancia que viajó horizontalmente, en
metros, después de que el jugador golpeó la pelota.
De acuerdo con la información anterior, considere las siguientes proposiciones:
I.
La pelota tiene mayor altura cuando ha recorrido una distancia horizontal
igual a 30 m que cuando ha recorrido 50 m.
II.
El tiro más largo es 46.4m.
De acuerdo con lo anterior, ¿cuál o cuáles afirmaciones son verdaderas?
A) Solo l
B) Solo ll
C) Ambas
D) Ninguna
Habilidad 10. Analizar sistemas de dos ecuaciones lineales con dos
incógnitas.
Sistemas de ecuaciones lineales
Se denomina sistema de ecuaciones lineales de dos incógnitas se satisfacen de
forma simultánea, estas ecuaciones son de la forma 𝑎𝑥
2
+ 𝑏𝑦 = 𝑐 y pueden
tener una solución, infinitas o no tener solución. Existen varios métodos:
1. Suma y resta: Consiste en multiplicar un número conveniente a cada lado
de la igualdad de manera que permita eliminar una de las incógnitas para
así lograr obtener el valor de la otra. Una vez obtenido este valor se
sustituye en cualquiera de las dos ecuaciones.
2. Sustitución: Este método consiste en escoger una de las dos ecuaciones y
despejar cualquiera de las dos incógnitas y sustituirlo en la ecuación no
elegida, esto brindará el valor de una incógnita, por lo que finalmente se
sustituye ese valor encontrado en una ecuación.
3. Igualación: Consiste en elegir una variable y despejar en ambas
ecuaciones, seguidamente igualar los resultados y así encontrar una
incógnita, para luego sustituirla en cualquiera de las dos ecuaciones
Interpretación gráfica:
I.
Sistema Independiente: Cuando el sistema de ecuaciones lineales es de
la forma:
si 𝑚1 ≠ 𝑚2.
II.
Sistema Incompatible: Cuando el sistema de ecuaciones lineales es de la
forma
y 𝑚1 = 𝑚2 , 𝑏1 ≠ 𝑏2
III.
Sistema dependiente: Cuando el sistema de ecuaciones lineales es de la
forma:
y 𝑚1 = 𝑚2 , 𝑏1 = 𝑏2
Ejemplo
Considere las siguientes situaciones:
I.
Kathia adquiere 2 manzanas y 1 naranjas por un monto de 5000 colones
mientras que Ana compra 2 manzanas y 1 naranjas, pero de diferentes
calidades de manzanas y naranjas. Ana paga la suma de 2000 colones.
¿Cuál es el precio de cada manzana y naranja de Kathia?
II.
Berta adquiere 1 corrector y 2 borradores por un monto de 2000 colones
mientras que Ana compra 2 correctores y 4 borradores, pero de diferentes
marcas de correctores y borradores. Esteban paga la suma de 4000
colones. ¿Cuál es el precio de cada corrector y borrador de Berta?
De acuerdo con las situaciones anteriores, ¿Cuál o cuáles no tiene
solución?
A) Solo l
B) Solo lI
C) Ambas
D) Ninguna
Habilidad 11. Plantear y resolver problemas en contextos reales,
utilizando sistemas de dos ecuaciones con dos incógnitas
Aplicación de los sistemas de ecuaciones.
Este proceso es una herramienta útil para la interpretación y resolución de
problemas a través de un sistema de dos ecuaciones lineales de dos variables de
forma tal que se entrelace con casos de la vida cotidiana.
Pasos a seguir para la resolución de problemas:
1. Tener claridad sobre lo que trata el problema antes de empezar a resolverlo.
2. Considerar varias formas para resolver el problema y seleccionar un método
específico para el problema.
3. Monitorear el proceso y decidir cuándo abandonar algún camino que no
resulte exitoso.
4. Revisar el proceso de resolución y evaluar la respuesta obtenida.
Ejemplo
¿Cuál es el área de un rectángulo sabiendo que su perímetro mide 36 cm y la
diferencia entre su largo y ancho?
Tema 3. Estadística y probabilidad
Las aplicaciones más antiguas, de que
se tiene constancia, de la Estadística
parece que tuvieron lugar en Egipto
Safnkit hace unos 5000 años: se trata de
sus
censos.
monumentos
encontrado
En
los
antiguos
egipcios
documentos
se
han
interesantes
que muestran la sabia organización y
administración de este pueblo; llevaban
la cuenta de los movimientos de la
población y hacían censos muy a
menudo. Hasta tenían a la diosa de los
libros y de las cuentas llamada Safnkit.
Según esta documentación, el censo se debía hacer bajo la dirección del
faraón y fue a partir del año 3050 a.C. cuando se empezaron a realizar los
trabajos censales. Estos trabajos censales se elaboraban cada año para
repartir los bienes y propiedades tras las crecidas periódicas del río Nilo. En
concreto, está perfectamente documentado un censo de las tierras que hizo
Ramsés
II
(1290-1224
(Compostela,2010,p.6)
a.C.)
para
realizar
un
nuevo
reparto.
Actividades deportivas
En un colegio se le preguntó a un grupo de 14 estudiantes de séptimo por el tiempo
que se dedica a realizar actividades deportivas por horas semanales y se registraron
sus respuestas en la siguiente tabla:
3
4
5
1
3
6
9
10
2
1
5
7
8
5
De acuerdo con la información anterior conteste las siguientes preguntas:
1. ¿Cuál es el tiempo dedicado en actividades deportivas con menor cantidad de
horas semanales?
2. ¿Cuál es el tiempo dedicado en actividades deportivas con mayor frecuencia en
las cantidades de horas semanales?
3. ¿Cuál es el tiempo dedicado en actividades deportivas con mayor cantidad de
horas semanales?
Habilidad 1. Resumir un grupo de datos mediante el uso de la moda, la
media aritmética, la mediana, los cuartiles, el máximo y el mínimo, e
interpretar la información que proporcionan dichas medidas.
Medidas de posición
Las medidas de posición son medidas estadísticas que pretenden resumir en un
solo número la localización o posición de la distribución de datos. La moda, la
mediana y la media aritmética son medidas de posición central.
Mínimo: Es el menor valor presente en un grupo de datos. Se denota por 𝑀𝑖𝑛.
Máximo: Es el mayor valor presente en un grupo de datos. Se denota por 𝑀𝑎𝑥 .
Moda: Es el valor que está presente con mayor frecuencia en el conjunto de datos.
Se denota con 𝑀𝑜. Puede no existir o puede no ser única.
Ejemplo 1: La siguiente tabla muestra las notas obtenidas en un curso:
80
85
90
90
92
85
85
80
85
Determine la Moda, la calificación mínima y la calificación mayor.
● La 𝑀𝑜 es _______________
5, ya
● El 𝑀𝑖𝑛 es _______________
80, ya que es la calificación mínima.
● El 𝑀𝑎𝑥 es _______________ 92, ya que es la calificación mayor.
Ejemplo 2: La siguiente tabla muestra la edad de los estudiantes:
17
16
17
15
16
17
16
17
16
Determine la Moda, según la información anterior:
● La 𝑀𝑜 es _____________________ 𝑀𝑜 es ,17 y 16, ya que son los datos que
más se repiten y se repiten la misma cantidad de veces.
Mediana: Es el valor que representa una serie de datos ordenados; es decir, un
valor tal que el 50% de los datos son menores o iguales a él y el otro 50% son
mayores o iguales que él. Se denota por 𝑀𝑒.
Para encontrar el valor de la mediana hacemos lo siguiente:
1. Lo primero que hacemos es ordenar los datos de menor a mayor.
2. Ubicamos la posición de la mediana con esta fórmula:
Posición de la mediana:
𝑀𝑒 =
𝑛+1
2
Si tenemos una cantidad de datos impares, la mediana estará posicionada donde
indique la fórmula anterior, pero para datos pares, la fórmula anterior nos dará un
número decimal, así que vamos a tomar los dos números entre los cuáles me da el
decimal, y lo dividimos en dos.
Ejemplo 1. (Datos impares)
Un profesor aplicó un exámen a 11 estudiantes de una sección. La siguiente tabla
muestra los resultados de las calificaciones.
96
92
92
93
98
92
100
93
97
96
Con base en la información anterior determine la mediana del grupo de
calificaciones e interprete los datos:
96
Ejemplo 2. (Datos pares , la posición de la mediana nos da en decimales)
Un estudiante realizó una encuesta a un grupo de 10 personas para saber las
notas obtenidas en un curso de física. La siguiente tabla muestra los resultados:
80
90
91
92
80
96
95
92
96
Con base en la información anterior determine la mediana del grupo de
calificaciones e interprete los datos:
98
Media aritmética o promedio: Se obtiene al sumar todos los datos y dividir este
resultado entre el número total de datos. Se denota por 𝑥 .
Observaciones:
● Para calcular la Media, los datos no necesitan estar ordenados.
● Media y Mediana suelen confundirse, pero la Media es un sinónimo de
promedio.
La fórmula se representa de la siguiente forma:
𝑥=
𝑥1 +𝑥2 +𝑥3 +...+𝑥𝑛
𝑛
Ejemplo: La siguiente tabla muestra las notas obtenidas en un curso:
80
85
90
90
92
85
85
Determine la Media e interprete los datos:
80
85
Cuartiles: Los cuartiles son medidas de posición que dividen un conjunto de datos
ordenados en 4 partes iguales. Se representan por 𝑸𝟏, 𝑸𝟐 𝒚 𝑸𝟑 y separan,
respectivamente, el 𝟐𝟓%, el 𝟓𝟎% y el 𝟕𝟓% de los datos ordenados. Observe que el
cuartil 2, el igual que la mediana, ya que ambos representan el 50%.
Para calcular los cuartiles se debe hacer o siguiente:
Ordenamos los datos de menor a mayor:
El grupo de 𝒏 observaciones deben estar ordenadas
Calculamos la posición del cuartil buscado:
Se utiliza esta fórmula para calcular los cuartiles:
● La posición 𝑷𝒌 del cuartil 𝑸𝒌 está dada por:
𝑃𝑘 =
𝑘(𝑛+1)
4
● Si 𝑷𝒌 contiene decimales ( cantidad de datos 𝒏 par), para calcular el cuartil
se usa la fórmula:
𝑄𝑘 =
𝑎+𝑏
2
donde 𝒂 𝒚 𝒃 son los datos de las posiciones entre las que se ubica 𝑷𝒌.
Al obtener el resultado, finalmente se da la interpretación de la medida de posición.
Ejemplo. Las emergencias realizadas en un hospital los últimos 12 días de
diciembre son las siguientes:
32
36
38
38
43
45
32
28
29
32
36
48
Según la información anterior determine:
El cuartil 1: R/
El cuartil 3: R/
⬜⬜⬜⬜,⬜⬜
Interpretación: ___________________
⬜⬜⬜⬜,⬜⬜ Interpretación: ___________________
Habilidad 2. Describir relaciones entre dos o más eventos de acuerdo
con sus puntos muestrales, utilizando para ello las operaciones: unión
“∪”, intersección “∩” y “complemento” e interpretar el significado dentro
de una situación o experimento aleatorio.
Teoría de conjuntos y eventos
Un conjunto es una agrupación de objetos, llamados elementos. En la mayoría de
los casos la agrupación de los elementos se realiza con un criterio que permite
identificar cuándo un objeto determinado pertenece o no a la agrupación.
Espacio muestral: Se define un espacio muestral como el conjunto formado por
todos los posibles resultados que pueden suceder en un experimento aleatorio, los
cuáles se llaman puntos muestrales.
Evento: Un evento es un conjunto formado por elementos del espacio muestral. Los
eventos se representan con letras mayúsculas, que por lo general son las primeras
letras del abecedario.
● Si los elementos de un evento son los mismos elementos del espacio
muestral, el evento se denomina seguro.
● Si el evento es el conjunto vacío, se llama imposible.
● Si el evento es un conjunto unitario, el evento se llama simple.
Las operaciones más usadas en teoría de eventos, tomadas de la teoría de
conjuntos son la unión, la intersección y el complemento.
Unión “⋃”
A ⋃ B , es el evento en que un elemento pertenezca al conjunto A o al B
Intersección “⋂”
A ⋂ B, es el evento en que los elementos pertenezcan a ambos conjuntos.
Complemento
𝐶
(A ⋃ B) , es el evento en que los elementos no pertenecen a ninguno de los dos
conjuntos.
Ejemplo 1. Sea el espacio muestral E= {1, 2, 3, 4, 5, 6, 7, 8}, el cual corresponde a
los puntos muestrales de un experimento. Este espacio muestral contiene los
siguientes eventos A= {1, 2, 3}y B= {4, 2, 3}
Determine A ⋃ B, A ⋂ B y el complemento (A ⋃ B)
𝐶
Ejemplo 2. Sea el espacio muestral E dado por E= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}, el
cual corresponde a los puntos muestrales de un experimento. Para este espacio
muestral se definen los siguientes eventos aleatorios:
A: Obtener un número divisible por 3.
B: Obtener un número mayor o igual que 6.
Considere las siguientes proposiciones:
I.
II. El evento de A está compuesto por 3 puntos muestrales.
III. A ⋂ B= {6}.
De ellas, ¿cuál o cuáles son verdaderas?
A) La I y II
B) La II y III
C) Solo la II
D) Solo la III
Habilidad 3. Representar mediante diagramas de Venn las operaciones
entre eventos.
Operaciones entre eventos con diagramas de Venn
Anteriormente estudiamos operaciones como la unión, la intersección, el
complemento de dos o más eventos dependiendo de sus puntos en un espacio
muestral, pero mediante diagramas de Venn podemos visualizar por medio de
representaciones a las operaciones que están ocurriendo entre eventos del
experimento estudiado.
Usualmente un diagrama de Venn son representados por círculos dentro de
rectángulo donde podemos representar por medio de la siguiente imagen:
Ejemplo:
Sean A ={1, 2, 4, 7, 9, 10, 28} , B = {1, 5, 7,6 ,8, 10} y C= {1, 2,3,6,7}. Coloque los
eventos A, B y C en un diagrama de Venn.
Solución:
Habilidad 4. Reconocer eventos mutuamente excluyentes en
situaciones aleatorias particulares.
Intersección de Eventos
La intersección de dos eventos dados A y B se define como un nuevo evento en
donde A y B ocurren simultáneamente y se denota por A∩B.
Ejemplo
Si se elige un número del 1 al 10 al azar. Si A es el evento de que salga un número
impar y B es el evento de que sea mayor que 4. Entonces A∩B es el evento de que
el número sea impar y mayor que 4.
Defina
E = Todos los números del 1 al 10
A = Número impar
B = Número mayor que 4
Entonces A∩B = {5,7,9}
Lo puede visualizar de una mejor
manera con un diagrama de Venn
Eventos mutuamente excluyentes
Sean A y B dos eventos, se dice que ambos eventos son mutuamente excluyentes si
A∩B es vacía.
Ejemplo
Si se elige un número del 1 al 10 al
azar. Si A es el evento de que sea
un número impar y B es el evento
de que sea un número par.
Entonces A∩B es el evento de que
el número sea impar y sea par.
Defina
E = Todos los números del 1 al 10
A = Número impar
B = Número par
Entonces A∩B = vacía.
Lo puede visualizar de una mejor manera con un diagrama de Venn
Ejemplo
Considere el siguiente diagrama de Venn, donde se han representado los eventos
A ={1,2,3,8} , B ={7,4,6,8,2,9} y E ={5,10} , respecto al universo de los enteros
positivos del 1 al 10.
De acuerdo con esto, conteste la pregunta
Dos eventos mutuamente excluyentes son
A) A y B
B) A∪B y A∩B
C) B y 𝐸
𝑐
D) A y E
Habilidad 5. Determinar la media aritmética en grupos de datos que
tienen pesos relativos (o ponderación) diferentes entre sí.
Media aritmética ponderada
Es una medida de tendencia central, es apropiada cuando en un conjunto de datos
cada uno de ellos tienen un peso relativo respecto a los demás datos. Se obtiene
multiplicando cada uno de los datos por su peso para luego ser sumados obteniendo
así un ponderado; después se divide éste entre la suma de los pesos de los datos
dando como resultado la medida ponderada:
𝑛
𝑥=
∑ 𝑥𝑖𝑝𝑖
𝑖=1
𝑛
Donde cada 𝑥 𝑖 tiene un peso 𝑝𝑖.
∑ 𝑝𝑖
𝑖=1
Ejemplo
Considere la siguiente información
Calificación estudiante
Evaluación
Nota
Porcentaje
Parcial I
90
20
Parcial II
85
20
Parcial III
70
20
Exposición
60
20
Otras evaluaciones
75
20
¿Cuál es la media aritmética (promedio) del estudiante?
R/
⬜⬜⬜⬜,⬜⬜
Habilidad 6. Utilizar la media aritmética ponderada para determinar el
promedio cuando los datos se encuentran agrupados en una distribución
de frecuencias.
Ejemplo: Una estudiante de la universidad obtuvo las siguientes calificaciones
en el curso de topología de la matemática, para una calificación de 0 a 10
donde la nota mínima para aprobar el curso es de 6.8.
Analice la siguiente tabla para apreciar las calificaciones que obtuvo en el
curso de topología la estudiante Leda.
Evaluaciones
Calificaciones
Primer examen corto
6.8
Segundo examen corto
5.8
Tercer examen corto
7
Proyecto
6
Primer parcial
7
Segundo parcial
8
Tercer parcial
7
De acuerdo con la información anterior de las calificaciones de Berta si los
exámenes cortos tiene un valor 5% cada uno, proyecto 20% y el primer
parcial 20%, segundo parcial 20% y el tercer parcial 25%.
Determine la forma en que podemos ponderar las evaluaciones del curso de
Topología de la Matemática de la estudiante Leda
Habilidad 7. Aplicar los axiomas y propiedades básicas de
probabilidades en la resolución de problemas e interpretar los resultados
generados.
Axiomas básicos de la probabilidad
Espacio muestral (Ω)
Es el conjunto de todos los posibles resultados de un experimento.
Ejemplo: El espacio muestral de lanzar un dado, es:𝑆 = {1, 2, 3, 4, 5, 6}
Punto muestral
Los puntos muestrales son los eventos de un espacio muestral.
Ejemplo:
Al lanzar un dado numerado de uno a seis, cada uno de los posibles resultados se
considera un punto muestral de este experimento.
Evento simple
Está formado por un único punto muestral.
Ejemplo:
Al tirar un dado, la probabilidad de obtener el número 2.
Evento compuesto
Está formado por varios eventos simples, es decir con más de un punto muestral.
Ejemplo:
Al tirar un dado, la probabilidad de obtener números pares.
Evento seguro
Es aquel que se tiene la certeza que se va a dar, en este caso el evento coincide
con todo el espacio muestral, así se garantiza que se va a cumplir.
Ejemplo:
Al tirar un dado, la probabilidad de obtener números menores o iguales que seis.
Evento imposible
Es un evento que no tiene posibilidades de que se llegue a cumplirse en ese
experimento aleatorio, es decir, nunca se va a verificar. Visto como conjunto este
evento sería un conjunto vacío.
Ejemplo: Al tirar un dado, la probabilidad de obtener el número siete.
Evento probable
Es aquel que tiene algunas posibilidades de que se dé. Estas posibilidades hacen
que, aunque nos sea un evento imposible, tampoco sea uno seguro.
Es el cociente entre la cantidad de veces que sucede un evento favorable y el total
de eventos posibles, es decir
𝑃(𝐴) =
𝑛ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑒𝑣𝑒𝑛𝑡𝑜𝑠 𝑓𝑎𝑣𝑜𝑟𝑎𝑏𝑙𝑒𝑠
𝑛ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑒𝑣𝑒𝑛𝑡𝑜𝑠 𝑝𝑜𝑠𝑖𝑏𝑙𝑒𝑠
Ejemplo:
Al tirar una moneda al aire, ¿Cuál es la probabilidad de obtener corona ?
Eventos posibles: corona y escudo (son dos eventos posibles)
Eventos favorables: corona (un evento favorable)
𝑃(𝐶) =
1
2
= 0, 5
Regla del mínimo de una probabilidad
El valor numérico más bajo que puede tomar una probabilidad de un evento es cero.
Los eventos imposibles tienen como probabilidad cero.
𝑃(𝐴) = 0
Nota: Cuando 𝐴 𝑦 𝐵 son eventos mutuamente excluyentes,
𝑃(𝐴 ∩ 𝐵) = 0
Regla del máximo de una probabilidad
El valor numérico más alto que puede tomar una probabilidad de un evento es uno.
Los eventos seguros tienen como probabilidad uno, ya que el evento debe coincidir
con todo el espacio muestral.
𝑃(𝐴) = 1
Ley fundamental de la probabilidad
Una probabilidad siempre estará entre cero y uno. Los eventos probables cumplen
0 < 𝑃(𝐴) < 1
esta ley.
Regla de la suma de total de las probabilidades
La suma de todas las probabilidades de un experimento aleatorio es uno, es decir
todo el espacio muestral.
𝑃(𝐴1) + 𝑃(𝐴2) + 𝑃(𝐴3) +... + 𝑃(𝐴𝑛) = 1
Regla de la suma de probabilidades de eventos mutuamente excluyentes
La probabilidad de la unión de dos eventos mutuamente excluyentes es igual a la
suma de las probabilidades de cada evento simple.
𝑃(𝐴 ∪ 𝐶) = 𝑃(𝐴) + 𝑃(𝐵)
Regla de la suma de probabilidades de eventos que no son mutuamente
excluyentes
La probabilidad de la unión de dos eventos siempre es igual a la suma de las
probabilidades de cada evento simple menos la probabilidad de la intersección de
ambos eventos.
𝑃(𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴 ∩ 𝐵)
Regla del evento contrario o del complemento
La probabilidad del complemento de un evento es 1 menos la probabilidad de ese
𝐶
𝑃(𝐴) = 1 − 𝑃(𝐴)
evento.
Ejemplo:
Tome en cuenta el espacio muestral de lanzar dos monedas el cuál es:
𝑆 = {𝐸𝐸, 𝐸𝐶, 𝐶𝐸, 𝐶𝐶}
¿Cuál es la probabilidad de que salga al menos una vez escudo?
𝑃(𝐸) =
3
4
= 0, 75
¿Cuál es la probabilidad de que no salga al menos una vez escudo?
𝐶
𝑃(𝐸) = 1 − 𝑃(𝐸) = 1 −
3
4
= 0, 75
Ejemplo. Sea el espacio muestral E dado por E= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}, el cual
corresponde a los puntos muestrales de un experimento. Para este espacio muestral
se definen los siguientes eventos aleatorios:
A: Obtener un número divisible por 2.
B: Obtener un número mayor que 5.
C: Obtener un número primo.
Considere las siguientes proposiciones:
I.
𝑃(𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵)
II.
𝑃(𝐵 ∩ 𝐶) = 0
III.
𝑃(𝐴 ∪ 𝐶) = 𝑃(𝐴) + 𝑃(𝐶) − 𝑃(𝐴 ∩ 𝐶)
IV.
𝑃(𝐴 ∪ 𝐵 ∪ 𝐶) = 1
De ellas, ¿cuál o cuáles son verdaderas?
A) La I y II
B) La II y III
C) La III y IV
D) Ninguna
Habilidad 8. Utilizar probabilidades para favorecer la toma de
decisiones en problemas vinculados con fenómenos aleatorios.
Resolución de problemas
Ejemplo. Considere la siguiente información sobre 4 bolsas que contienen bolas de
diferentes colores.
De acuerdo a la información anterior, conteste las siguientes preguntas:
1.Para obtener la mayor probabilidad de extraer al azar un balón de color blanco o
azul se debe elegir la bolsa #___.
A) 1
B) 2
C) 3
D) 4
2. Para obtener la menor probabilidad de extraer al azar un balón de color rojo o
blanco se debe elegir la bolsa #___.
A) 1
B) 2
C) 3
D) 4
Bibliografía
Compostela, B. (2010). Breve historia de la Estadística y el Azar. Recuperado de
https://umer.es/wp-content/uploads/2015/05/n62.pdf
Faro de contenido Gratuito de Dibujo Clipart - Cristiano Faros Cliparts - Faro, Libre
De Contenido, Dibujo - Imágenes gratuitas de alta calidad.
https://www.freepng.es/png-ua9nza/
Fuller, G. y Tarwater, D. (1995). Geometría Analítica. Séptima edición. Pearson
Educación. Recuperado el 28 de junio de 2021 de:
http://up-rid2.up.ac.pa:8080/xmlui/handle/123456789/1483
[Imagen]. (s. f.). Recuperado de
https://3.bp.blogspot.com/-cn4Bc-c7KbY/VPRVwTYplhI/AAAAAAADlBs/eCL_y
H87ous/s1600/ESTUDIANTES%2B(126).png
Imágenes de Graduación: sombreros, diplomas, libros, y más
https://www.freepng.es/png-bmur6h/download.html
Jiménez, J. (S.F). Funcion lineal. Recuperado 22 de septiembre de 2021, de
https://www.geogebra.org/m/YxHkgqeB
Lorente Morata, A. (S.F). Historia del algebra y de sus textos. Recuperado de
https://d1wqtxts1xzle7.cloudfront.net/38983595/Historia_del_algebra_y_de_su
s_textos-with-cover-page-v2.pdf?Expires=1630713604&Signature=ROhAew9
4hZBAtNk1DK7ZU1IkvZRLhsXwcGkjoVdV437m-z5FWl3fXqAGzNMa1yDcOa
ShdFgroGvF7J2P8A29hqUF77bS6MDtwvKKRyM7D47DHb0azCsJCUwp8Jy2
4ajVGy562qhF~N0vDk5MS1K6xLLGUNOWy6dcG~h2~KVapKJM9VjDGSnyD
lEVQ0mu4ZHrCNtY8V09fulFkSqVHVSN9o2LqdUTIzalhOktOUhMbLaqw9Xxc
dAQRq5r9fRjB~J8tQlpImTPtVj96eAsk3e9OtBY2NKfqewVtOgytZSHtCzAzrEr
LkhYIm3IAWILYDfa~AirqtmNozLRGwz2wdxkow__&Key-Pair-Id=APKAJLOHF
5GGSLRBV4ZA
Martínez, C. (S.F). Rectas horizontales y verticales. Recuperado 22 de septiembre
de 2021, de https://www.geogebra.org/m/cVgwQMXC
Miguel, A. (S.F). Animación de la función cuadrática. Recuperado 22 de septiembre
de 2021, de https://www.geogebra.org/m/jVKqWYFy
OpenClipart-Vectors. (2015, 2 enero). [Imagen]. Recuperado de
https://pixabay.com/es/images/search/pirámide%20egipcia/
WikiImages. (2013, 3 enero). [Imagen]. Recuperado de
https://pixabay.com/es/photos/jerogl%C3%ADficos-diosa-reina-fara%C3%B3n
-67471/