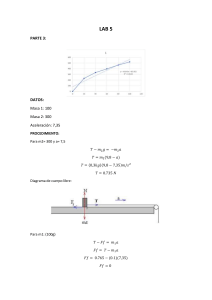
PÉRDIDAS POR FRICCIÓN EN TUBERÍAS Y ACCESORIOS RESUMEN Los sistemas de flujo de un fluido presentan ganancias de energías por bombas y pérdidas por fricción conforme el fluido que pasa por los ductos y tubos, pérdidas por cambios en el tamaño de la trayectoria de flujo y pérdidas de energía por las válvulas y accesorios. La realización de este informe de laboratorio tiene como propósito identificar, analizar y calcular las pérdidas por fricción de un fluido en un sistema con tuberías y accesorios. Palabras Claves: energía, flujo laminar, flujo turbulento, factor de fricción, número de Reynolds. BASES TEÓRICAS Las pérdidas por fricción se presentan porque al estar el fluido en movimiento habrá una resistencia que se opone a dicho movimiento (fricción al fluir), convirtiéndose parte de la energía del sistema en energía térmica (calor), que se disipa a través de las paredes de la tubería por la que circula el fluido. Las válvulas y accesorios se encargan de controlar la dirección o el flujo volumétrico del fluido generando turbulencia local en el fluido, esto ocasiona una pérdida de energía que se transforma en calor. Estas últimas pérdidas son consideradas perdidas menores ya que en un sistema grande las pérdidas por fricción en las tuberías son mayores en comparación a la de las válvulas y accesorios. Las pérdidas y ganancias de energía en un sistema se contabilizan en términos de energía por unidad de peso del fluido que circula por él. Esto también se conoce como carga (h): Energía que se agrega al fluido con un dispositivo mecánico; es común que se le denomine carga total sobre la bomba. Energía que se remueve del fluido por medio de un dispositivo mecánico. Pérdidas de energía del sistema por la fricción en las tuberías, o pérdidas menores por válvulas y otros accesorios. La magnitud de las pérdidas de energía que produce la fricción del fluido, las válvulas y accesorios, es directamente proporcional a la carga de velocidad del fluido. Esto se expresa en forma matemática así: El término K es el coeficiente de resistencia. Ecuación general de le energía: La ecuación general de la energía es una extensión de la ecuación de Bernoulli, lo que permite resolver problemas es los que hay pérdidas y ganancias de energía. Para un sistema, la expresión del principio de conservación de la energía es: y : denotan la energía que posee el fluido por unidad de peso en las secciones 1 y 2. La energía que posee el fluido por unidad de peso es: Es esencial que la ecuación general de la energía se escriba en la dirección del flujo. El comportamiento de un fluido, en lo que se refiere a las pérdidas de energía, depende de que el flujo sea laminar o turbulento. Un medio para predecir este comportamiento en el flujo es con el manejo del número adimensional Reynolds, demostrado por Osborne Reynolds. Esta ecuación de define como: Re= = Donde es la velocidad, es el diámetro de la tubería, la densidad del fluido y la viscosidad del fluido. Es de resaltar que es la viscosidad cinemática. Este número relaciona las fuerzas de inercia sobre un elemento de fluido a la fuerza viscosa. Para aplicaciones prácticas se tiene que los flujos con Re <2000, se encuentran en estado laminar, y los Re>4000, están en régimen turbulento. Los 2000<Re<4000, están en la región de transición o región crítica. Por lo general si un sistema llegase a estar en esta región, se debe jugar con las variables de Re, para acondicionarlo en un estado netamente conocido, como lo son el laminar o el turbulento. Teniendo en cuenta la ecuación general de la energía, es de resaltar que el término hL es la pérdida de energía en el sistema. De forma matemática esta se expresa a través de la ecuación de Darcy: hL = Donde f es el factor de fricción, L la longitud de la corriente, D el diámetro de la tubería, la velocidad promedio de flujo. Este factor de fricción, f, se evalúa dependiendo del régimen en el que se encuentre el fluido. Una vez se tenga certeza del régimen en el que se está, se aplica alguna de estas expresiones: , para flujo laminar. , para el régimen turbulento. Los términos , hacen referencia a la rugosidad relativa, donde es la rugosidad promedio de la pared del tubo. La ecuación para el flujo laminar se determina a partir de la ecuación de Hagen-Poiseuille (ciertas simplificaciones lo llevan a la ecuación de f para el flujo laminar). La ecuación para el flujo turbulento fue desarrollada por Swamee-Jain. Cabe resaltar que otro de los métodos indispensables para evaluar el factor de fricción es el Diagrama de Moody, el cual muestra la gráfica del factor de fricción versus el Re, con una serie de curvas paramétricas relacionadas con la rugosidad relativa.En los anexos se muestra esta. Es importante resaltar que las pérdidas por fricción también se dan por los accesorios que posean las tuberías, para esto siguiente: se aplica la relación hL = Donde es el factor de pérdida para el accesorio. En los anexos se muestra una tabla con los valores para algunos accesorios. DESCRIPCIÓN DEL EQUIPO El equipo para la determinación de las pérdidas de carga por fricción, dispone de los accesorios más representativos y habituales que las originan. En el siguiente cuadro, se describen las especificaciones y el empleo de dichos elementos en el desarrollo de la práctica. ACCESORIOS ESPECIFICACIÓN O TIPO EMPLEO Tanques. Fabricados en HDPE. Alimentación y recirculación. Bombas. Centrifuga. Probé deenergía al fluido. Válvulas PVC cedula 80 de tipo diafragma de membrana. Estudio y calculo del factor de fricción. Válvula de compuerta tipo regulación de flujo V2 de ¾ de pulgada. Válvula de bola V1 de ¾ de pulgada fabricada en PVC. Válvula de bola V3 de una pulgada fabricada en PVC. Válvula de asiento inclinado tipo regulación de flujo V4 de una pulgada fabricada en PVC. Válvula de bola V5 de media pulgada fabricada en PVC. Válvula de compuerta tipo regulación de flujo V6 de ¾ de pulgada fabricada en PVC. Válvulas fabricadas en acero inoxidable y conector rápido. Lectura de presión diferencial en diferentes puntos. Válvulas de asiento inclinado. Regulación de flujo laminar en experimento de Reynolds. Válvula de bronce Rotámetro Reducciones y ensanchamientos De flotador Medición de flujo. De una pulgada a ¾de pulgada Estudio y cálculo del factor de fricción De una pulgada a media pulgada fabricada Tuberías de experimentación Codos Ensayo de Numero de Reynolds en tubería 180°: de ¾de pulgada Y de media pulgada. 90° °: de ¾de pulgada, de una pulgada y de media pulgada. para estudio y cálculo del factor de fricción 45°: de una y media pulgada. Divisores Y de 3/4 y una pulgada. T de 3/4, media y una pulgada. Placa de orificio cálculo de flujo tubo de Venturi cálculo de flujo, convergente – divergente Otros. Dispositivos de inyección de tinta, Manovacuometro, Sensor electrónico de presión, Medidor de voltaje y amperaje. REVISIÓN DE LA TÉCNICA 1 2 3 1- Primeramente se define los tramos a analizar, done no se tiene en cuenta accesorios. 2- Se especifican diferentes caudales con el Rotámetro. 3- Se toman las lecturas de caída de presión para cada caudal con el sensor electrónico de presión. En esta práctica se analizó un tramo corto de 0,5 m y otro tramo de 1 m. En cada caso se midió la caída de presión con diferentes caudales. DATOS DE CAMPO Temperatura ambiente: 30°C. CAUDAL Presión: 1 atmosfera. CALCULOS Y RESULTADOS Datos y propiedades: Suponiendo una temperatura ambiente de 30°C. Diámetro interno de un tubo de ¾ in de PVC CD-80: VELOCIDAD (m/s) 1 2 REYNOLDS 1 2 (L/min) m3/s 4 0,00006667 2,51E-01 5.757,81 8 0,00013333 5,01E-01 11.515,62 12 0,00020000 7,52E-01 17.273,44 16 0,00026667 1,00E+00 23.031,25 20 0,00033333 1,25E+00 28.789,06 24 0,00040000 1,50E+00 34.546,87 TRAMO TRAMO TRAMO TRAMO 18,4mm= 0,0184m Área transversal del tubo: Viscosidad cinemática a 30°C. . En la siguiente tabla se mostrarán los caudales con las caídas de presión experimentales: CAUDAL (L/min) 1. Primero determinamos la velocidad mediante la relación de: 2. Luego hallamos las propiedades a la temperatura a la se encontraba, para determinar el Re del flujo con la expresión que se mencionó anteriormente. En la siguiente tabla encuentran tabulados resultados: se los 4 8 12 16 20 24 CAIDAS DE PRESIÓN (KPa) PRIMER SEGUNDO TRAMO TRAMO 0,2 0,18 0,33 0,25 0,52 0,4 0,77 0,62 1,11 0,87 1,47 1,12 Gráfica: Caídas de Presión en los Tramos 1,6 Caídas de Presión 1,4 1,2 1 0,8 Primer Tramo 0,6 Segundo Tramo 0,4 0,2 0 0 5 10 15 20 25 30 Caudal Ahora se mostrará los valores obtenidos a partir de cálculos teóricos, teniendo en cuenta que se aplicó la ecuación de balance de energía, con las respectivas simplificaciones a las que el sistema a estudiar se acomodaba: Simplificando queda que: Las perdidas por fricción se expresan como sigue: El valor de f se determina, teniendo en cuenta el régimen del fluido, cabe resaltar que todos estuvieron bajo el régimen turbulento, por lo que se aplicó la expresión: Ahora, la caída de presión en este tipo de sistema, está dada por las perdidas por fricción en la tubería. El cálculo de , se efectúa de la siguiente forma: El valor de , es de 61333,33333, donde el valor de = 3,00E-07 m. Los resultados continuación: se muestran CAUDAL (L/min) a Los datos tabulados de caída de presión y caudales teóricos, se muestran a continuación, junto con la grafica la cual describe el comportamiento funcional de estas variables: f 4 8 12 16 20 24 0,036294646 0,029834597 0,026829376 0,024966940 0,023654537 0,022658914 CAUDAL (L/min) 4 8 12 16 20 24 CAIDAS DE PRESIÓN (KPa) PRIMER SEGUNDO TRAMO TRAMO 0,06174766 0,20302902 0,41080055 0,67961546 1,00607977 1,38777652 0,03087383 0,10151451 0,20540028 0,33980773 0,50303988 0,69388826 Gráfica: Caída de Presión en los tramos 1,6 Caídas de presión 1,4 1,2 1 0,8 Primer Tramo 0,6 Segundo Tramo 0,4 0,2 0 0 10 20 Caudal CONCLUSIONES Y RECOMENDACIONES Conclusiones: 30 A medida que se aumente la longitud del tramo en donde se realizan las mediciones pertinentes a la caída de presión, estas van a ser mayores, por lo que se verifica la proporcionalidad que hay entre la perdidas de energía y la longitud como lo muestra la expresión: hL = Un aumento en el caudal produce una elevación en las caídas de presión, debido a que, en una sección de tubería de área constante, la velocidad va a ser mayor, por lo tanto las pérdidas de energía se incrementaran en un factor cuadrático, pues: hLα Las diferencia entre las medidas experimentales y teóricas, radican en parte a la sensibilidad y calibración del manómetro, pues cualquier entorpecimiento del sistema hacia que los datos arrojados cambiaran abruptamente. Recomendaciones: Hacer limpieza periódica al fluido con el que se trabaja para minimizar los errores con los cálculos de fricción. Suministrar de manera más precisa los datos de temperatura y presión. Calibrar los manómetros del equipo correctamente.