Puerto-de-palos-1ro-activados-4-pdf

os
AcT¡vA
o
R¡E
o
MATEMATICA
o
ffi$PrnRToDEPrros
Gen¡¡r¡ EIltroRtAt
Coono¡rloom o¡ D¡ssf,o
Daniel Arroyo
Natalia Udrisard
ferr orl Anrl o¡ Mnr¡mÁncl
D¡s¡f,noom
Gabriel H. Lagoa
Patricia Cabezas
Auron¡s
D¡lcmmlcró¡
Roxana Abálsamo
Adriana Berio
Cintia Kotowski
Lourdes Liberto
Silvana Mastucci
Gabriela Prandini
Nora Quirós
Susana Vázquez
Foto Activados: Laura Pezzatti
Pablo Alarcón y Alberto Scotti para Cerúleo
Conn¡cron
DE
Esnlo
DE mAeuETA
llusrmoon¡s
Wally Gómez
Viñetas de humorz Claudio Kappel
Forocm¡fls
Archivo de imágenes de Grupo Macmillan
Latinstock
Thinkstock
Wikimedia commons
Gabriel Valeiras
G¡n¡rr¡ o¡ Pn¡pn¡rs¡ v Pnooucc¡ór Eorron¡lt
Carlos Rodríguez
Matemática 1 : fotoactivados / Roxana Abálsamo ... [et.al.]. - 1a ed. 2a reimp. '
Boulogne: Puerto de Palos, 2013.
224 p: il.; 28 x 20 cm - (Activados)
tsBN 978-987-547 -527 -4
1. Matemática.
2.
Enseñanza Secundaria. 3. Libros de Texto. l. Abálsamo'
Roxana
cDD 510.712
@ Editorial Puerto de Palos S.A., 2012.
Editorial Puerto de Palos S.A. forma pafte del Grupo Macmillan.
Av. Blanco Encalada 104, San lsidro, provincia de Buenos Aires, Argentina.
lnternet: www.puertodepalos.com.ar
Queda hecho el depósito que dispone la Ley 77.723.
lmpreso en Argentina.
Printed in Argentina.
rsBN 978-987-547 -527 -4
La presente obra se ha elaborado teniendo en cuenta los aportes surgidos de los encuentros organizados por
el "lnstituto Nacional contra la Discriminación, la Xenofobia y el Racismo" (lNADl) con los editores de texto.
No se permite la reproducción parcial o total, e[ almacenamiento, e] alquiler, la transmisión o la
transformación de este tibro, en cualquier forma o por cualquier medio, sea electrónico o mecánico, mediante
fotocopias, digitalización y otros métodos, sin el permiso previo del editor.
Su inftacción está penada por las leyes 11.723 y 25.446'
Primera edición, segunda reimpresión.
Esta obra se terminó de imprimir en enero de 2O74, en los talleres de lmpresiones Sud América,
Andrés Ferreyra 3769, Cíudad Autónoma de Buenos Aires, Argentina.
AcT¡vA
o
a
o
a
MATEMATICA
o
KIPU¡nro
DE Pnros
T
I I
f
Es una nueva propuesta que facilita el aprendizaje de [a matemática a través de
635 actividades que favorecen [a comprensión de los distintos temas.
En formato binarizado, la sección Foto Activados conecta la matemática con la
vida cotidiana a través de la fotografln.
Fncn y llllFA son los personajes de esta serie. Les gusta mucho sacar fotos, principalmente
de todo aquello que los hace recordar algún tema de matemática. Así, le encuentran sentido a
todas las cosas que aprenden día a día en la escuela.
lilnn
LOS CAPíTULOS INCLT'YEN I.AS S¡GUIENTES SECCIONES Y PI-AQUETAS:
APrRrunn: cada capítulo comienza
con una actividad ilustrada
relacionada con la foto que aparece
en la sección Foto Activados.
En la situación iniciol de
aprendizaje se introduce el tema del
capítulo a través de una estrategia de
resolución de problemas.
lrrollrrwn:
En el cuadro de
contenidos aparecen los
temas numerados para su
fácil identificación.
brinda
defi niciones, clasifi caciones,
procedimientos básicos y
ejemplos de cada contenido
que facilitan la comprensión.
Ii,iÍl:::I-";
r..¿ .;;
L--
l:=:=,_
:t,&*;:"-a
¿ tEs¿\ .=
g;grh,ffi
ffi..1
'if":ffi"
f,nnecron: invita a repasar
conceptos explicados en páginas
anteriores.
Trnr ug EomPnEnsúft íncluye
preguntas básicas que permiten
evaluar la comprensión de la teoía y
revisar errores comunes.
I
Acrlvnnn¡¡i para cada tema se
proponen distintas actividades que
están organizadas de manera
secuencial (las actividades de cada
capítulo ltevan una numeración
independiente a la de los otros).
¡r¡rr¡AlTlVA:
propone
ones problemáticas con un
nivel de complejidad.
lnrgannclún! incluye más
actividades para resolver en la
carpeta.
Auorvnlunf,túfl ! propone
más actividades para que cada
alumno.pueda evaluar los
conocimientos adquiridos
durante el capítulo.
FOIO
Tnnen¡ns FHAETtEos:
incluyen más actividades para
practicar los temas del
capítulo.
lCtivAdos:
en esta sección, Laura
Pezzalti, especialista en el área de la matemática,
ofrece una serie de actividades que conectan [a
matemática con la vida cotidiana a través de la
fotograflia.
Foco y Mira presentan las fotos que obtuvieron
para que podamos advertir cuánta matemática hay
nuestro alrededor.
a
Crpfrulo l: nÚmrRos NATURAIES .............. 8
l. Sístema de numeración decimal. ......... 9
E. Multiplicación y división.
Propiedad distributiva. ........................ 11
3. Potenciación y radicación. ................. 13
h. Operaciones combinadas. .................. 15
lnr¡cn¡c¡ún
......................
19
S. Divisibilidad y factorización. .............. 27
E. Múttiplo común menor
y divisor común mayor. ..................... 23
7. Lenguaje simbólico. Ecuaciones. ........ 25
...................... 29
lnr¡cnncÉn
Auto¡vttulc¡ót
................................
€rpfrulo il: FRACCIONES
y EXPRESTONES DECIMALES
31
......................... 32
B. Orden y representación. ..................... 33
ll.
Fracciones equivalentes. .................... 35
Crpfrulo
l+:
cuERPos
.............74
lE. Clasificación de los cuerpos. ..............
........
El. Poliedros regulares.
75
77
flE. Desarrollo plano de cuerpos. .............79
..... 83
t3. Punto, recta y
...................... 85
Auro¡vlluecrót ................................ 87
plano.
lnt¡cnmún
Clpfrulo 5: Aneutos
............ 88
tl+. Sistema sexagesimal. Operaciones. ...... 89
Ángulos complementarios
y suplementarios. ............................... 91
ffi.
EE. Ángulos adyacentes
y opuestos
por eI vértice. .....................................
87. Mediatriz de un segmento
y bisectriz de un ángulo. ...................
......................
Auro¡vllunc¡ór ................................
lnffsnA$ún
93
95
97
99
l[1. Operaciones con números
racionales.
ll.
Potenciación
...................... 37
y radicación
de fracciones. .....................................
41
lE. Operaciones combinadas
con fracciones. ................................... +¡
...................... 47
lnrscnñún
13. Fracciones y expresiones decimales. ....49
Crpfru¡.o E: FIGURAS PLANAS. .................. 100
tE, Triángutos. Elementos'
y propiedades. ................................... 101
35. Construcción de triángulos. ............. 103
10. Cuadriláteros. Elementos
y propiedades. ..................................
31, Construcción de cuadriláteros. ......... 109
lnr¡snmún
ll+. Operaciones con expresiones
decimales. Porcentaje. ....................... 51
l$. Operaciones combinadas. .................. 55
...................... 57
lnrscR¡c¡ún
Auro¡vl¡.unctót ................................
59
107
3t.
.....................
113
Círculo y circunferencia. Elementos
y propiedades. ...................................
115
ll. Construcción de circunferencias. ....... 117
......779
3\, Polígonos. ................
ll5. Construcción de polQonos
Crpfru¡.o l: FUNCIONES ............................. 60
............ 61
lE. Gráficos y tablas.
17. Funciones.
E.
lll.
................
....... 65
Función de proporcionalidad directa. ... 67
Función de proporcionalidad inversa. ... 69
lmm¡ffi1
Auro¡vlturcrót
...................... 71
................................ 73
regulares.
lnreenAcún
....727
.................... 125
727
..............-...............
Auro¡vlr.urcrón
COLEGIO SANTA ROSA
SEDE YERBA EUENA
CIpfruIo 7: PERÍMETRO,
Y
AREA
VOTUMEN
Tnnen¡os
........ 128
3G. Perímetro y área de
figuras planas.
37. Area lateral y total de prismas,
pirámides y
cilindros.
... 733
38. Unidades de capacidad y
unidades de volumen. ...................... 737
l$. Volumen del prisma, de [a pirámide,
del cilindro y del cono. .................... 139
lnrssnncrún
Auro¡vllulc¡ór
lonrRol
..............
.......... 746
Td. Variables, población y muestra ....,.,. 747
\1. Recolección y organización
de datos. Tablas.
.......... 749
\8. Frecuencias absolutas y relativas. ....... 151
l+3. Gráficos.
.... 753
lntecRm¡ún
.................... 157
l+\. Promedio, mediana y moda. ............ 159
l+5. Experimentos aleatorios.
Probabilidad
..':..76t
simple.
combinatorio ...... 763
lnrrcnAflfi
.................... 165
t+8. Cálculo
Auro¡vlLulcró¡
.......... ........,:.,..,..... 767
Clpfrulo 9: nÚmeRos
ENTERoS ............. 168
l+7. Números negativos.
Orden
y representación. ...................
sustracción
TE. Adición y
t+ll. Multiplicación
Trabajo
Trabaio
Trabajo
Trabajo
Trabajo
Trabajo
Trabajo
Trabajo
Trabajo
práctico
práctico
práctico
práctico
práctico
práctico
práctico
práctico
práctico
................ 180
1 .............................. 181
2 ............................ 183
3 ............................ 185
4 ............................ 787
5 ............................ 189
6 ............................. 191
7 ............................ 193
8 ............................ 195
9 ....................,....... 797
.................... 143
.............................. 145
C¡PÍIUIO E: PROBABILIDAD
y EsrADfsflcA
pnAErE¡s
769
...... 777
y división. ................. 773
50. Operaciones combinadas. ..............,. 775
lrnrsn¡cfin
.................... 777
Auro¡ylrulctó¡
.......... .......:...,......... 779
0E nEsur?Aro¡ ............................... 199
f,onrrnru¡s
i"
Sistema de numeración
decima[.
Multipticación y división.
Propiedad distributiva.
Potenciación y radicación.
Operaciones combinadas.
Divisibitidad y factorización.
Múttipto común menor y
divisor común mayor.
Lenguaje simbótico.
Ecuaciones.
hié
\a
1:F
f"A
l'
F
..v:''rÉA
': ,il-
\le
t
'=:¡&=::*.=-,:...¡
¿-
^ ---,.'-"_-
r:::=:=L_:::=h*
Srrulc¡ó¡ tiltcrAl
DE APRENDTZATE
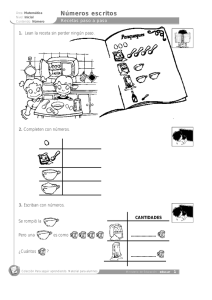
1. Observen la imagen y resuelvan.
a. Si todos van a ir al Circo Mógico, ácuánto dinero deberán pagar en total de entradas?
Escriban un cálculo para encontrar el resu]tado.
b. Si solo van a ir algunas personas, inventen situaciones que se respondan con cada uno de
los siguientes cálculos. Luego, respóndanlas.
'2.73+2.30:
o
3.13 +2.3O+ 4.20=
c. Comparen las situaciones que inventaron con las de sus compañeros.
SErEnrnEt
Sistema de numeración decimal
Nuestro sistema de numeración es:
. decimal, porque utiliza diez símbolos: O, 7, 2, 3, 4, 5, 6, 7, 8 y 9.
. posicional, porque el valor de cada cifra depende de la posición que ocupa en e[ número.
billón
mil de
millón
míllón
mil
TTT
T
1 000 000 00 oo oo
\Bs\ss!5s
stssssSts
\q¡AJ\qJq)Es)AJ
\s
sc
.Ba)
sg\s8\58\
5q)
u'\u'\u
SSotSuqss
q\
AJ 'B
ss
U.E
\f
Los números naturales se pueden descomponer de distintas formas. Por ejemplo:
35042=3OOOO +5OOO + 40 +2
35042 =3 . 1OOOO + 5 . 1OOO + 4 . 10 + 2.
35O42 = 3 . 1Oa + 5 . 1O3 + 4. 101 + 2. 1Oo
Se
\-
lee:
treinto y cinco mil cuarenta
y
1
dos.
2OO4OO1OOOO =2OOOOOOOOOO + 4OOOOOOO + \OOOO
2OO4OO\OOOO = 2 .1OOOOOOOOOO + 4 .1OOOOOOO + 1 .1OOOO
2OO4OOTOOOO = 2. 1O1o + 4. 1O7 + 1 . 1O4
'tt
\-
5e lee: veinte mil cuarenta millones diez mil.
Todos los números se pueden escribir como una suma de productos en los cuales uno de los
factores es una potencia de base 10.
Las unidades de un número se pueden expresar como el producto entre este y una potencia de
diez de exponente cero (tengan en cuenta que todo número elevado a la cero es igual a uno).
1. Respondan y expliquen las respuestas.
a. ZCuál de las descomposiciones del número 3085 es correcta?
3.7O2+8.101+5.100
3 . 103 + 0 . 102 + 8 . 101 + 5 . 100
b. En la descomposición del número 38548794, Zel 5 se multiplica por 105 o por 106?
c. ZEs verdad que 1000000000 es igual a 1.le?
d. iEs cierto que 10 es uno de los símbolos del sistema de numeración decimal?
I
ACNUDADES
Sistema de numeración decimal
1. Unan con flechas cada número con su descomposición.
.4.108 + 4.707 + 8.106 + 8.105 + 8.103 + 4.100
a.4048080380
4.
8.
8.
b.4480080840
o
8.
102
c.480388800
o 4 .lOe + 4 .707 + 8 . 106 + 8 . 10a + 3 . 102 + 8 .
1.01
d.448808004
o 4 .7Oe +
108 +
4.
107
+3.
108 +
105 +
10a +
8.
8 . 107 + 8 . 10a + 8 .
103 +
102 +
4.
101
2. Completen para gue se verifique la igualdad.
a. 6 . 107.
b.
1. 1Oe + 1.106
c. 9
.
d. 8 .
3.
O.
7012
1OO+ 3 . 102 + 2 . 100 = 60050302
O.1OO+ 1. 101 = 1001501010
+ 9 . 707.
O . 1OO+ 9 . 103 : 9OOOO90019OOO
1014.O.
+5
.105.
1OO+ 8 . 106 + 3 . 105 + 5 . 100 = 800000908300005
Escriban ia descomposición en potenc¡as de diez de los siguientes números.
a.4O4O4O4 =
b.78675675 =
c.742208056
:
4. Marquen con una X las
r expfes¡ones
expresiones que corespondan al número 360306.
a. Trescientos seis mil trescientos
+6
b. 300000 + 6000 + 300
0o+6
c.3
seis.
C
O
.707 + 6.105 + 3.103 + 6.101
d. Trescientos sesenta mil trescientos seis.
o
(
e. Tres centenas de mil, seis decenas de mil, tres centenas y seis unidades.
O
f. 3 . 106 + 6 . 105 + 3 . 103 + 6 . 101
g.
3.
105
+ 6.7Oa+
3.
102
+6. 100 O
h. Trescientos millones sesenta mil trescien tos
¡. 300000 + 60000 + 300 + 6
C
seis.
O
5. Rodeen con color el número que cumple con las condiciones dadas.
Es mayor gue doscientos mil y menor que doscientos diez mil. El valor de dos de sus cifras
equivale a 5 . le y 3 . 1ü. La cifra de las unidades es el doble de tres.
205356 215t56 206536
205303
Hnffiffiffi#Mu*u
Multiplicación y división. Propiedad distributiva
Los números que intervienen en una multiplicación y en una división tienen nombres especiales.
Muttipticación
\
a.b.:¿
\2
^
factores
A'
División
dividendo D
lt
'ñ.
ld
c
divisor
\-/' \-/
resto
cociente
D:d.c+r
Conmutativa: el orden de los factores no
cambia el resultado.
Asociativa: si se cambia el orden de los
paréntesis, e[ resultado no cambia.
6.8=8.6
(5.12).4=5.(12.4)
Disociativa: un factor se puede descomponer
en otros factores.
Elemento neutro: el número 1 como factor
no cambia e[ resultado.
15.1 =1 .15=15
7.24=7.(2.12)
Propiedad distributiva de la multiplicación
3.(4+5)=3.4+3.5
(9
-
3)
.2=9.2-3.2
Propiedad distributiva de la división
(2+Q:2=12:2+4:2
(15-g):3=15:3-9:3
En la división, solo se puede distribuir el divisor.
1. Respondan y expliquen las respuestas.
a. Si se multiplica un número por uno, Zqué número se obtiene?
b. aA qué es igual 532 . 7ü iCómo se puede resolver aplicando propiedades?
c. Los cálculos (3 + 6) .5 y 3 + 6.5, Ldan el mismo resultado?
d. ZCuál es el resultado de 0 : 5? LY de 5 : ü
e. Los cálculos (15 + 20) : 5 y 5 : (15 + 20), Ldan el mismo resultado?
f. Para obtener e[ resultado de 120 : (10 + 2), ise puede aplicar la propíedad distributiva?
ASTIVIDADES
Multiplicación y división. Propiedad distributiva
6.
Expresen las siguientes sumas como multiplicación, si es posible,
y resuelvan.
b.2+2+2:
d.3+4:
e.5+4+21:
c.4+4:
f.9+9+9:
a.3+3+3+3=
7.
Escriban
V
1.3:1
b.3.0:3
a.
8.
(Verdadero) o F (rabo), según conesponda.
C
c.0.0:0
d.to:10:o
o
e.0: 10:0
f.to:o:o
o
o
Resuelvan las siguientes divisiones.
d.to8:tz:
a.45:3:
b.78 : 6 :'
c.140 : 10 :
9.
I
Completen con
e.248:8:
¡. t26o
= o *,
a.3 + (2 + 4 + 7) [,
+
40)
2o
I
:
según conesponda. Expliquen la respuesta.
. 2 + 3 . 4 +7
.5O ro .5 + 40 .5
c. (6 + 72) :6!
u :6 +72:6
b. (zo
z
d.(zo+40):5Oro +4025
e. 120 : (20 + 40)
O
f. (165 - 9o) : tt O
10. Resuelvan de dos manera¡ diferentes, cuando sea posible.
720
165
:20 +
:75
-
720
9o :
: 4o
15
e
I
I
InErwwwwfi
Potenciación
radicación
Potenciación
La potenciación es una operación que permite escribir en forma abreviada una multiplicación de
factores iguales.
42 = 4
.4 = 16
"cuatro elevado al
cuodrodo"
43 = 4
o Para multiplicar dos potencias de igual base, se
escribe la misma base y se suman los exponentes.
.
.4 .4
=
64
32 .33
'cuatro elevado al cubo"
=3
.3.3.3 .3
Z2+3
-U
Para dividir dos potencias de igual base, se escribe
-.)
25
25:22 = (2.2.2.2.2): (2.2)
_ .>5-2 _ o3
la misma base y se restan los exponentes.
-L
e Para calcular la potencia de otra potencia, se escribe
la misma base y se multiplican los exponentes.
-L
(5r), = (5 .5)u
=(5.5),(5,5).(5.5)
_
-¿
.
^2.3
_
-J
^6
(4 .3)" = 42 .32
La potenciación es distributiva con respecto a la
multiplicación y a [a división.
(12:4)z = 122 :42
Radicación
La radicación es [a operación inversa a la potencíación.
W=3,porque7'=27
tl64 - B,porqueS2 =64
Se
lee'la
raíz cuadroda de 64 es 8".
Se lee
. La radicación es distributiva con respecto a
'lo raíz cúbico de 27 es 3".
.',9.16 = ''[9 .,[16
ta multípticacíón y a la divísión.
,t64'16 ="[64'\n6
o Para mulüplicar o dMdir níces de igual índice,
se escribe una raíz con el mismo índíce y con el
radicando igual a la multiplicación o división de
los radicandos dados, según
1. Respondan y expliquen las respuestas.
a
ZCuáles son los cuadrados de los primeros diez números? ZQué raíces pueden calcular conociéndolos?
b. El procedimiento
c
30
.3
.32 :31, ies correcto?
Para resolver 4[76, ¿se debe calcular 1.6 : 4?
ACTIVIDADES
Potenciación
y
radicación
11. gscdban el desanollo de cada potencia y resuelvan.
=
a.72
e. 105
:
:
g.5a :
d.4,:
h.6¡:
b.35=
c.7a
:
Í.2e
J
12. Escriban cómo se lee cada potencia.
a.25
b.322
c.23:
f
13. ¡scriban como potencia los siguientes productos y resuelvan.
d.!O=7-7.r=f-l
".OO:5.5 t:[-l
o'Oo:2'2'2'2'2'2
:6.6.6.6:f--l
".CO
*CO=e.e.n:f:]
"CO--'..'=f]
14. Completen con V (Verdadero) o F (rabo).
a. (s + 3)2:52
b. (s .
3)2
:
¡32 O
5z .32
c.(8-\)t:gz-42
d. (8:
o
c
fJ:
t
b. ./25 : C, porque
Ü : ,t
c lB = [-1, oorou. $ : t
d.fi=[-.),oorou.S:t
e. .lroo : O, porque fJ : too
{e = [-1,
oorou.
gz
' 4z
e.23 :32
Í. (2r)2 :
15. Completen con los números que faltan.
a.
\)z:
f.
g.
h.
t.
i.
27 .22
IE
:
'E
m
10, porque
f
O
o
o
1oO:
f-l
80: (-l
:2, porque 20: t
= 8, porque
lE
m
=
11, porque
flO :
'I
f
t-l
: 5, porque sO = t-l
16. Resuelvan aplicando propiedades, cuando sea posible.
a.23 .23
b.
1012
:
.2
1o1o
.2o
:
. 1o =
f../Z
9.,175 :
i/t
cga3:g1o.g25|.g57:
h.
d. (3)' .32 =
¡.{a1
e. (10. 2:5)2
:
. {18- =
.
{3
1,125
:
=
.16.a:
i.1t64.T-:ú
c
ffiffiffir*-r
Operaciones com binadas
SEDT
\
Para resolver una operación combinando todas las operaciones, se pueden seguir estos pasos.
2
1. Se separa en términos.
2. Se resuelven las potencias y raíces
(aplicando las propiedades cuando
2.6+12:2+25.3-36=
12+6+75-36=
93 -36=
sea posible). I
3. Se resuelven las multiplicaciones y
divisiones.
4. Se resuelven las sumas y restas.
.t|56 + 12 : 2 + 52 . 3 - 615 . 6b'. 621 =
2.6+12:2+25.3-62=
-
6'7
En ta págína 15
podrán repasr las
propiedades de la
potenciación y [a
iYAf,EgrARnl,AúA
bÉ
qr,oqwAu6
sF6rbsE8l
radicación.
g
W,
Si hay operaciones en el radicando o como base de una potenciación, se deben resolver antes
de calcular la raíz o [a potencia.
3 - (15 :3 - Z1z + 144 : 12 =
.,85;12 .5;3 - (15 : z - z7z + i44 : 12 =
- p - 3)" + 144 : 12 =
^tE¡56;3
,t64-22+12=
1. Se separan los términos.
B-4+12=
3. Se resuelven las potencias y raíces.
4. Se resuelven las sumas y restas.
"[Ú + 12.3
+
=16
2. Se resuelven las operaciones que hay
en e[ radicando y en la base de la
potencia respetando la ierarquía.
1. Respondan y expliquen las respuestas.
a. En e[ cálculo 10. (5 + 4) :3, ase separó en términos correctamente?
b. ZEn qué orden se deben resolver las operaciones que encierran los paréntesis?
c.iCómosesuprimenlosparéntesisene[
operaciones que ellos encierran?
d.
ZEs
cierto que',[z .
tz *
L t : let
cálculo(3+8).2+6.(5+4),sinresolverlas
ACÍIVIDADES
Operaciones combinadas
17. Resuelvan.
a.2.r/81-42=
e.25 . {t00 + 3.42 =
I
b.(50.2-62272)0=
c. (lT +
13)¡
f.^,[s, +50;16
:
+^lE .g-33
=
g. (o . n1 + 3 . 5 . 74 -1m : ^[7$ =
J
d. {1oO + "{25
:
(22
+
50)
-
14
=
h. (z' + \b6l .
^lV
.72 .3
:
f
18. Escriban el cálculo y resuélvanlo.
a. El doble de la raíz cuadrada de veinticinco.
b. La raíz cuadrada del doble de cincuenta.
J
c
La raíz cúbica del triple de setenta y dos.
d. E[ cuadrado del producto entre diez y el doble de cinco.
e. El cuadrado de la resta entre el cubo de cinco y cien.
,
f. El doble de la suma entre dieciocho y el cubo de tres, menos veintitrés.
ACTlvlDADES
Operaciones combinadas
19,
A.
Resuelvan aplicando las propiedades de la potenciación
317
:315 +
{G
y la radicación, cuando sea posible.
tL23.2.23+5.<IOiA3:
=
)
:7 + (2')' .({ñ - 16 . l-¡O
b.52.5.5+{8:{2=
1.
42
c
t
fuo-600ll0 * {to . úooo
L
f{Ñ
1oo
:
(102
-
s, . 3) - lTboolrot =
=
=
)
ir. (41" . 43 z (4t12
-
32 : 76 =
)
)
f. (./6I
*
)
+
{9) : 22 + 517 : 516 =
"'E ..'[27 + (10 +
3)'?
;'@
¡n
=
+ 74 .
^[4¿r:.
4+
: .,[49 .
15a
:A.
r'-480
: 60 =
(¡ - lB- + 2') :
n. (3e)': (3'5 . 3) * r/ro . (z * r)
-Y:
ACNUDADES
Operaciones combinadas
20. Completen con {, } o
_
r-r
e{+. lo uo.{36
b,26 .t [8r.1r.lr
-
según conesponda.
- 63[tt, + 63 - r22
,-r
f../mO . 102 + t [-f 1 + 102 . \ho-d
cl2, . (21,1D (2'o .2,)
4[u . t'
d.164 .
,'f
+
e.
112
g.
{2d . ./5
h.i6t
r22
+
22
lt'
D
(l'
+./i6
O40
.
Í
+ o : 52 + t/El
Marquen con una X el cálculo que coresponde a cada situación y rcsuelvan.
e. iCuál es el resultado de la suma entre el cubo de la raíz cuadrada de veinticinco y la raíz
cúbica del cuadrado de ocho?
2L
[-l
f]
zs' * ./at
aA qué es igual
b.
r.rzD,
.
te
f]
r
..,[25 +i/z-re-
el doble de la diferencia entre el cuadrado de cinco y la raíz cuadrada del
cubo de cuatro?
!,
2iL
({,
f]
.52-^[43
z
.$ . z- {-+')
f
z . (5'-./-43)
Completen.
nrñm:ffi='
fl
*iE+102=f-l*D=,0,
*
fJ
* i/rooo =
t
f:llJ
+ 720
si {G4 . 1oo
.
f::]* f]I]
zf-l= CJ
=,m
f"]
='o
+ 20 = 6e
. {10-o
.
fJ
fi
=D.ro*f-l=153
:
f-t-f-l,fIIIl:
"
menteACfl\lA
Para hacer un trabajo de educación artística, Luis y Juan deben cortar figuras de cartón. Luis
necesita doce cuadrados de 25 cm de lado y Juan, diez rectángulos de 15 cm por 42 cm.
ZCUánto mide la superficie de cada cuadrado? ZY la de cada rectángulo?
r
L iQuién usará
más cartón para cortar todas las figuras?
lr)
col{TEilTDOS
lnrEERAuún
23.
l.E.3.ll
Escriban los números que corresponden a
las siguientes expresiones. Luego, ordénenlos
de mayor a menor.
a.4Cdemil,SUdemily4u
b.4.706+8.103+4
28. Completen las operaciones teniendo
cuenta el siguiente dlculo.
30 .25 = 75O
a.6o.ru:f-:]
e.4.704+8.103+5.100
uO: zso
c.3) .25 : t-]
f. 400000 + 80000 + 80 + 6
d. 30
b.30.
c. 5 unidades de millón, 5 unidades.
d. 500000 + 6000 + 5
24.
Escdban el mayor y el menor número posi-
ble usando todas las cifras de cada uno de los
siguientes nfimeros.
29.
.25o:
t-l
Resuelvan las multiplicaciones
a.76.3.5 =
b.47.2.100:
c.32.6.10:30 =
d.15.426.5=
e.104.15:5.24=
f.450 t 90 .20 .73
h. 72 . 27 z 74 . 8 : 24
25. Marquen con una X el número que coresponde a la siguiente expresión.
1o5
a,4OO4397OO
+3.
104
+ 9 . 10t + 1.
102
y divisiones.
:
9.8100:923.5=
4. tú + 4,
:
Completen con = o É, según conesponda.
Expliquen la respuesta.
30.
a.3.4f]+
+4+4
b.(3+O.rC3.2+8.2
C
[-l
zo'
b,404309100
c
c.400403970
d.(2+8).(8.tO2+8.8+3
26.
Descompongan cada número de tres for-
mas diferentes.
a.500647
b.7206787
c 400004
1o
: (20 + 3o)
e. (zo + 30) :
10O
1o + 3o : 1o
ro : 10 + 30 : 10
f.(3+O.rO3+8.2
d.948999
e. 35772 048 910
Í.
6200 200 200 200
31. Resuelvan.
*3+4.72-7022:
b. (3 * 4) .12 -70
27.
en
Respondan.
a. En una división el cociente es 20, el divisor es el doble de 72 y el resto es la cuarta
parte del cociente. iCuát es el dividendo?
b. Al multiplicar dos números, se obtiene
9526. Si uno de los factores es 11, icuál es el
otro factor?
:2
=
c-3+4.(12-70):2:
d.3+(4.72-70)':2=
32. Resuelvan aplicando la propMad disüibutiva
a. (384 + 336) :72 =
b.35.(42-18):
c27.(72+75-27)=
d.(105-40+75):5=
e.(t6+8-10).26=
Qt¡lo:-
Fúta:.-/-/-
33.
Escriban un par de paréntesis para obtener
el resultado indicado.
a. t2 + 56 : 8 2 + 36 :74
b.100: 50 - 5.5 + 8 6 =52
c 34 - 76 : 2 + 7 2 :12
d. t5 + 3 18 - 50 : 2 + 26:43
34.
- 770 .2 =
b.100.7-70.5+8.9:
c.76.4+8:2-4.2=
d. 158+(78:2-27):
e.372 + (28 + 36:4) -119:
. (23')o :
a.
b.
2318
c
(10ú)10 .7012a
658
.23) .23 :
(2330
: (68¡t ,61e . (62)2:
: (tgtolro : 1070 =
d. 15.VF.ffia'lf=
e. lG. ls
'17 =
i..,[91 3+.J44 =
35. Escriban V
(Verdadero) o F (Falso), según
conesponda. Expliquen las respuestas.
a.3a:72
=23
d. {100
la iguatdad en cada caso.
¿28.2.2'/=20
751 71 76
O *s)'=x
e.32+O:t,
d' {/D ' ?'1725 =
.e. (3)' , (¡ .
731 71 6
31612
st7t25
5
¡O .39 :
31412
s
O
40.
O /-\
: 50 L_J
t r/9 + 'l-te :.{E D
O
O
lt6'r O
{7 = {16
h. lG. ,11 =
.
t
7271 71 27
e.(3+2+5)2:32 +22+52
'V8-
Rodeen con color el valor que hace cierta
D
b. (¡ . ))s :3s .2s
L32
39.
b.
f.543-(25.5+76:2):
36.
Resuelvan aplicando las propiedades.
Resuelvan.
a. 340 .2 + 72O .3
s.
38.
Escriban e[ cálculo
y resuélvanlo.
a. La resta entre e[ cubo del doble de diez y
el triple deI cuadrado de cuarenta.
b. La resta entre e[ cubo de seis y la mitad
de la raíz cuadrada de cuatro.
c. Et triple del producto entre e[ cuadrado de
dieciséis y la raíz cuadrada de dieciséis.
d. La mitad de la mitad del triple del cuadrado de dieciséis.
q
e. La mitad de [a raíz cúbica de la resta entre el
Completen.
cuadrado de diez y e[ cuadrado de seis.
f.
La tercera parte de la diferencia entre
ochenta y seis y cinco, aumentada en [a raíz
cuadrada de ciento sesenta y nueve.
41.
".c.o
f.(84-ze):['l=o-o=o
37. Escriban
el cálculo y resuélvanlo.
a. La tercera parte del cubo de seis.
b. La raÍz cuadrada de la suma entre ocho y
cincuenta y seis.
c La raíz cuadrada de treinta y seis, más la
quinta parte de doscientos cincuenta.
rt
Resuelvan.
aú00.4+53-3.r7=
b. (125 *^[-g).+:
c102.3+92.5:
d. 10 . (106 . 10e : 1012) - 1gr =
e. fu00-lr6llT + 82:
i. 25 z (2e : 27 + 16) + 4 .70 =
g.{(2.8:r/64+50).3:
¡. 1,[[ ¡l - r/4 + 3 . (27 : 64) :
a. <ltB + 1m . 5t -,[@ :
¡. 8 . ({900 + r/r 6oo
-
\D500-)
(,
:
mnn snmmml
Dluis¡biüdad y fiadorizacién
Un número a es divisible por otro b, cuando a : b es exacta, es decir, tiene resto igual a 0.
3 es divisor de 15
15 es divisible por 3
15 es múltiplo de 3
Cribr,b de divisibiüdad
Un número es divisible por:
.2, cuando es par.
¡7
Ejempto
.
3, cuando la suma de sus cifras es un múltiplo de 3.
o 4, cuando sus dos últimas cifras son ceros o múltiplos de 4.
. 5, cuando termina en 0 o en 5.
. 6, cuando es divisible por 2 y por 3 a la vez.
. 9, cuando la suma de sus cifras es un múltiplo de nueve.
. o 10, cuando termina en 0.
)7
76;174
153;6231
12;3OO
BO;315
138;942
198;9O9
50;23O
Un número es primo cuando tiene dos divisores: ell y el mismo número. Por ejemplo, 5 es primo,
ya que tiene como divisores et 1 y el 5.
Un número es compuesto cuando tiene más de dos divisores. Poreiemplo,T2es compuesto, ya
que tiene los siguientes divisores: 7,2,3, 4, 6 y 72.
Un número compuesto se puede descomponer de manera única en factores primos. A la descomposición se la denomina factorización. Para factorear un número, se pueden utilízar los siguientes
esquemas:
70
tt
l2
70=2.5.7
l?
rl
)
Para encontrar todos los divisores de un número, se puede realizar el siguiente procedimiento.
70=2.5.7
2.5=10 2.7=14 5.7=35.
Divisores de 70: 1; 2: 5; 7; 10: 14: 35:
)
L
70
1. Se factoriza el número.
2. Se calculan todos los productos posibles
de sus factores primos.
3. Todo número es divisible por 1 y por sí mismo.
y orpliquen las respuesta<.
a Para saber si un número es divisible por 6, talcanza con saber que es divisible por 2?
Respondan
b. iEs correcto decir gue 1 es un número primo?
c. E[ número 95356, ees múkipto de 4?
ACTIVIDADES
5
42.
Divisibitidad y factorización
Escriban los números que cumplen con la condición indicada.
a. Los múltiplos de 3, mayores que 120 y menores que 141:
f
b. Los múltiplos de 8, mayores que 200 y menores que 250:
c. Los divisores de 6:
d. Los divisores de 20:
e. Los divisores primos de 60:
43.
Escriban un número que cumpla con las condiciones dadas, usando las cifras
4,5,7 y8.
a. Múltiplo de 2, pero no múltiplo de 4:
b. Múltiplo de 4 menor que 7O0O:
c. Múltipto de
11
y par:
d. Divisible por 4 y que la cifra de las unidades sea menor que
D
8:
e. Divisible por 5 y mayor que 8000:
44. Marquen
una X, según conesponda.
fi
45.
Factoreen los siguientes números y exprésenlos como una multiplicación.
b. 600
c.1089
d.4470
a.792
792 =
46.
600:_-
1089:
4470:
Completen con la hctorización de los siguientes números. Tengan en cuenta el ejemplo.
oo eo
oo F
c72o=oo p co
a.280=oo
b.76s=co
m
co
co
e.2s7=co
d.3so:co
m
Í.3025=oo
oo
€
nnnmnmmnl
Múltipto común menor y divisor común mayor
El múltiplo común menor (mcm) entre dos números es el menor de [os múltiplos que tienen en
común esos números, sin tener en cuenta el 0.
4 son: o, 4, B, @, l o, zo,@
Atsunos múttiptos de 6 eon: o, o,@1 o,@, zo 2o...
-l
Algunos múrtipros de
I
1
2 ee el menor múltiplo
T::t"i;:á: ii^o^
Para hallar el mcm (12;30) se factorean los números y se eligen los factores para obtener el
múltipto común menor.
1213
,"o,
tlt" tZlZ 12=z.z.212.3O =3 .2.,2.L3,.5
3012
.5
mcm(12;30)=22.3,5=60
Para calcular el mcm se rnultipl¡cen los factores comunes y na
comunes con su mayor exqonente.
El dMsor común mayor (dcm) entre dos números es el mayor de los divisores que tienen en común
esos numeros.
I
Los divisores de 1B
Los divisores
de24
,12,24
JI
6 es elmayor delos divisores que
tienen en común.
dcm(18:24) =@
Para hallar el dcm (28;98) se hctorean los números y se eligen los fuctores para obtener el divisor
común mayor.
2Bl
2
141 z
2B=2.n
2 .7 es divisor comúnmayor entre2)y 98.
TI'
dcm (28:98) = 2
9b=,2.7,.7
.7 = 14
Para calcular el dcm se mul:tiplican los factorcs comunes con su tnenor
exponente.
1. Respondan y expliquen las respuestas.
a. Para calcular el mcm de dos o más números, asiempre hay que multiplicar los números?
b. Dos números son coprimos si su dcm es f. iDos números consecutivos siempre son coprimos?
c. ZCuáles son los factores primos comunes entre 10 y t5?
LY
los no comunes?
A TMDADES
Múltiplo común menor y divisor común mayor
47, Faúo¡een los siguientes números. Luego, hallen el mcm y el dcm en cada caso.
e
108
392
180
108 =
180
:
392 =
mcm (108;180;392) =
b.
200
20
dcm (108;180;392)
2
6
:
20=
000
200 =
2000:
mcm (20;200;2 000)
:
c60
36
dcm (20;200;2000) =
60=
6s
'
36=
fi
65=
mcm (60;36;65)
48,
Planteen
:
dcm (60;16;6S) =
y resuelvan.
a En un local de iluminación decoraron
la vidriera con tres tipos distintos de luces LED azules,
y
blancas lilas. Las luces azules se encienden cada 20 minutos; las blancas, cada 30 minutos y las
lilas, cada 15 minutos. iCada cuántos minutos se encienden simultáneamente los tres tipos de luz?
b. Un grupo de chicos recolectó 300 muñecas,42O pistotas de agua,480 pelotas y 600 rompecabezas para formar paquetes y regalar en el DÍa del Niño en un club det barrio. Si en cada
paquete colocarán la misma cantidad de cada juguete, Zcuál es [a mayor cantidad de paquetes
que podrán armar? ZCuántos juguetes de cada tipo tendrá cada paquete?
c. Juan va al club cada tres días, Santiago cada cuatro y Agustín cada seis días. Si fueron los tres
juntos el 1 de junio, icuándo volverán a encontrarse? iSe encontrarán el 23 de junio? iY el 25?
d. Para festeiar el DÍa del Amigo, Camila compró 12 esmaltes, 6 collares, 18 anillos y 36 caramelos. Si quiere armar bolsas de regalo con la misma cantidad de obsequios de cada tipo, ipara
cuántas amigas [e alcanza? iQué deberá colocar en cada botsa?
4
WWWWWWW
5
El tenguaje de las palabras, que puede ser oral o escrito, se denomina lenguaie coloquial.
La matemática utiliza un lenguaje particular denominado lenguaie simbólico.
Lenguaie simbólico
Lenguaie coloquial
3.x
a:4
b-1
Ellriple deunnúmero.
Lacuarla parte de un número.
El anl,erior de un número.
El doble de un número, disminuido en
2.x- 4
cuafro.
)
Si entre un número y ta tetra no se indica la operacibn, se entiende que hay un signo de muttiplicar.
6.x=6x
Una
eoacifu
es una iguatdaden [a que hay, por [o menot un valor desconocido [amado inoógnita.
x-3=20
7."
míembro
+
2.o miembro
Resolver una ecuación significa encontrar el valor o los valores de la incógnita que hacen verdadera la ígualdad. Cada valor de la incógnita es una solución de [a ecuación.
Para resolver una ecuación, se deben obtener ecuaciones equivalentes, es decir, con la misma
solución, teniendo en cuenta las siguientes propiedades.
. Se suma o resta un mismo número a ambos miembros de [a igualdad.
. Se multiplica o divide por un mismo número (distinto de cero) a ambos miembros de [a igualdad.
. Se aplica una potencia o raíz a ambos miembros de la igualdad.
x+3
= 12
x+5-3=12-3
x=9
x-
B =21
x-B+B=21 +B
x=29
t
6.x=42
xa=O1
<[¡
6.x:6=42:6
=W
X=7
x=3
x:5=B
Vx=5
x:5.5=8.5
?!x3 =
53
x= 125
x=40
1. Respondan y expliquen las respuestas.
a. E[ siguiente de un número, Zcómo se expresa en lenguaie simbólico?
b. iCómo se traduce x2 al lenguaje coloquial?
c La ecuación 5x + x + 2x = 56, Les equivalente a 7x
:
56?
@
tl
ACTIVIDADES
Lenguaje simbótico. Ecuaciones
49.
Traduzcan al lenguaje simbólico.
a. El doble de un número.[-l
b. El anterior del dobre de un
número.n
c. El doble del anterior de un
número.[-]
d. La mitad de un número.f-]
e. La diferencia entre un número y su
f.
anterior.[-]
El producto entre el dobre de un número y su consecutivo.
t-l
50.
Unan con flechas cada enunciado con la expresión simbólica conespondiente.
a. La tercera parte del cuadrado de un número.
.(¡:3)2
b. El cuadrado de la tercera parte de un número.
ox2:3
c. El producto entre un número y su cubo.
d. El cubo del producto entre un número y su cubo.
e. La mitad de la suma entre un número y su anterior.
f,
La raíz cúbica de la resta entre un número y su anterior.
.x.x3
.[x+(x-1)]:2
. ifi:-6a:l)
. (¡ . x3)3
51. Escriban un problema para cada una de las siguientes ecuaciones y resuélvanlas.
a.2.(x-5)=36
52.
b.x:2+24:2.75
Encuentren el valor de cada incógnita y verifiquen.
a.8+m=52
d.3+a:2=79
4
b.t-8:23
Q-Y3=25.2
c.3+x.2=79
f.{ñ=32+50
6
ACTMDADES
Lenguaie simbólico. Ecuaciones
53.
Resuelvan cada ecuación y verifiquen la soluclón.
a.3+x:^IB=B
b. 5x
-
22
=
,,[36
h.10x+15+4=37+4x
1.42+9x+{4=76.5+2+7x
c.x.(4+50)=5:
i.6x-6+3x=3x+6
d.r/9+xz3=32
k
C.5+x:2:2024
L9x+45-5x:76+5.6+3x
f.6x+3x+7.3=5+35.2
¡r. 6x + 343 : 72 - x = (2, + 1) : 5 + 14 + 3x
t 3x+50+x=25+1[I
n. 4x + 15 + 6x * i/8 : 2 = ú00 + 8x
3x+ 5x-49 = 2x+x+11
ACNUDADfS
Lenguaie simbólico. Ecuaciones
54. Resuelvan las siguientes ecuaciones aplicando la propiedad distributiva.
a4.(x+2)=29
e.77x-
5:5. Qx+7)-3
fl
b.36+59=QOx+10):2
16.(3x+5):3.(20+x)
f.3.(4x+6)=193
g.3.(x+2)=2.(x+2)+2
0
d. (x + 6)
.2+
79
= !87
h.3. (x-6) = (2x+1) . 5 -8.
9
55. Resuelvan las siguientes ecuaciones con potenciación y radicación. Verifiquen los resultados.
ax3+3.74:52.10+8
b. 3 . 100 + 26 + "lx
F
I
t
:72 .28
c(x-2)3+18:530
d
d.rF.T*r- =2.6
menteACTlVA
El triple de la edad que sebastián tendrá dentro de cinco años es iguat at dobte de ta
que tendrá dentro de 23 años. iCuát es la edad actual de
Sebastián?
edad I
I
fl
IntEEHAEún
56.
61.
Escriban.
a. Todos los divisores de 28.
b. Todos los divisores de 45.
c Todos los múltiplos de 15 mayores que
y menores que 90.
57. con las cifras 0, 2, I y 5 escriban
16
un
número que cumpla con las condiciones dadas.
a. Un número de cuatro cifras distintas que
sea múltiplo de 2 y de 5 a la vez.
b. Un número de cuatro cifras distintas que
sea divisible por 2, pero que no sea divisible
por
Resuelvan.
a. Si se divide un número por 3, por 5 y por
7, el resto es 0; pero si se [o divide por 6,
sobra 3. iCuál es el número?
b. Si al número de la actividad anterior se [o
divide por 2, i4ué resto se obtiene? iPor qué?
c Si se divide un número por 5, por 9 y por
7, el resto es 0; pero si se lo divide por 2,
sobra 1. Si se cuadruplica et número, iqué
número se obtiene?
d. iPor qué número se debe dividir 1548 para
que el cociente sea 642. ZCuál será el resto?
5.
c
Un número de cuatro cifras distintas que
sea divisible por 3, pero que no sea divisible
por 6.
62. tengan en cuenta la descomposición de los
siguientes números y escriban V (Verdadero) o
F (rabo), según corresponda. Expliquen la respuesta.
58. Resuelvan.
a. Marcos dividió un número por 15 y obtuvo
2700 = 22
.3 . 52 .7
2200 a
,52 .
_ resto 0.
a. 8 es divisor de z zoo.
.
.
iEl
iE[
o iEl
. iEl
. iEl
múltiplo de 15?
múltiplo de 3?
múltiplo de 10?
múttiplo de 5?
múltiplo de 30?
b. Florencia dividió un número por 8 y obtunúmero
número
número
número
número
es
es
es
es
es
vo resto 5.
. Si quiere convertir e[ número para que sea
divisible por 8, Zcuánto deberá sumarle?
. Si quisiera que el nuevo número fuera múltiplo de 80, ipor qué número deberia multiplicarlo?
59.
Factoreen los siguientes números
y expré-
senlos como multiplicación.
a. 1400 =
b. 1056 :
c 2500:
d.2835:
e,2548 =
Í.7O07 =
60.
Observen las siguientes potencias de diez
y respondan. Expliquen sus respuestas.
te3 to'¿ lozt le
a. iCuál expresa el dcm entre ellas?
b. iCuál expresa e[ mcm entre ellas?
21
t+41
ll
440
= 32 .72
= 23 .5 .11
[-l
b. 440 es divisible por zz. [-l
c. 49 es divisor de aa1.l-.]
' ''' l_J
d. 25 es divisor de 2100 y de 2 200. C
e.
22oo es divisibte por rs.
[-.)
f.
El dcm entre los cuatro números es 4.
g.
El mcm entre los cuatro números es:
23
.32 .52 .72.
y
h.
440
a.
22OO
441.
y
flo
son coprimos.
447
son.opritor.
[-.]
['l
k 2100 es divisible por 7, pero no por Ot.O
i.
1 es el dcm entre los cuatro
L
El dcm de 2100
63.
a
y
núteror.
22OO es:22
.5'.
C
Escriban.
Tres números mayores que 4
y que tengan
el 64 como mcm.
b. Tres números menores que 80 y que tengan el 20 como dcm.
Curso:-
Fecha'.-/-
64. Ha[ar el mcm y el dcm entre los siguientes nfimeros.
a. 60; 90; 150.
b.775;200; 280.
c
48; 80; 120; 180.
d.77; 7; 77.
e.84; 350; 450.
68.
Resuelvan.
a. Agustín y su hermana Belén completaron un
álbum de 420 figuritas deportivas. Agustín consiguió 162 figuritas más que su hermana. Six
representa la cantidad de figuritas que consiguió
Belén, icuál de las siguientes expresiones permi-
te calcular esas figuritas? ZCuántas figuritas obtuvo cada uno de ellos?
f.27;243;729.
x+
65.
a. Si el papá de Ema recibe una publicación
deportiva trimestralmente, una revista de
actual¡zac¡ón médica bimestralmente y un
suplemento deportivo europeo cada 5 meses,
Zcada cuántos meses recibe simultáneamente
las tres publicaciones?
b. La mamá de Andrea tiene 300 cintas verdes y 450 blancas para armar moños de rega1o. Si todos los moños deben tener la misma
cantidad de cintas de cada color, ácuántos
moños podrá hacer? iQué cantidad de cintas
verdes y blancas tendrá cada moño?
66. Planteen la ecuación y resuelvan. Luego
veffiquen.
a. El doble de la edad de Mariana es igual a
la mitad de cincuenta y seis. iCuál es la edad
de Mariana?
b. El precio de tres kilogramos de helado es
igual a cuatro veces cuarenta y cinco. ZCuánto
cuesta el kilo de helado?
c. El peso de Luca aumentado en seis es
igual a la mitad de veinte kilogramos.
420
x+ x=
x+162+x-162=420
162
Resuelvan.
=
t62 +
b. Dos amigas, Sandra y Andrea, han tejido
mantitas para vender. Andrea tejió 8 mantitas
menos que Sandra y entre ambas se comprometieron a entregar 60 mantitas. Six representa la cantidad de mantitas que tejió Sandra,
¿cuál de las siguientes expresiones permite cal-
cular esa cantidad? iCuántas mantitas tejió
iada
una?
8-x+x=60
x-8+x=60
69. ¡scriban la ecuación y
resuélvanla.
a. La suma entre el triple de un número y
el doble de su siguiente es igual a la mitad
de 84.
b. El cociente entre 20 y 5 es igual al dobte del
es el número?
70.
Resuelvan las ecuaciones e indiquen cuá-
les tienen la misma soluc¡ón.
a.{G4+x223=70+6.2
b.x+3x-812:811 :r/64
.3': (lfr ' 3m
d. La cuarta parte de lo vendido en el puesto
de panchos es igual a[ doble de ciento ocho.
iCuánto se vendió en total?
d.(54-5).x-25.70=250
y verifiquen.
!.(x+72):6-5=3
b.(x-3):3+20:42+8
c.5x-100:69-8x
d.6x-18+2x:3x+!7.6
c.3.(x+5)-2x+7=48t3
f. (x- 2) . 4 + 36 = 45 . 2 + x+ 4
I
anterior de un número, aumentado en 4. iCuál
c. (x + 2)
Resuelvan las ecuaciones
I
8-x-60=x
ZCuántos kilogramos pesa Luca?
67.
420
71. Resuelvan las siguientes ecuaciones con
potenciación y radicación. Veriñquen los resultados.
8.x2-
(36+2.5):2.32
b,25+x3:36+82+2.25
C,45:0+23)=3az
d.fi+6.8=52.2
e,(7+2)'?+rfi'=9.10
.5 :22 .32
f. rE + 6
I
AuroEvALUAcrón
72. Descompongan de tres formas diferentes.
26O62206 =
73. Resuelvan aplicando propiedades cuando sea posible.
".
b.
i
4 . (s . 7 + 7o) + 270 : 30
58
c.i[F
.
513
:
. +o
51e
+ (4 . 9 -
* zy
72)o
+ 102 . 5
-
(18
-
"'[45 : ^/5
-
4 . 2) =
:
:
74. Resuelvan.
8 horas y un analgésico cada 6 horas.
e. ZCada cuántas horas debe tomar los dos medicamentos juntos?
E[ médico le recetó a Florencia tomar ún antibiótico cada
b. iCuántas pastillas del antibiótico debe tomar por día? LY del analgésico?
75. Glculen el mcm y el dcm entre 675,
5¿O
y
180.
76. ¡sciiban en lenguaje simbólico y resuelvan. Verifiquen el resultado.
El doble de la suma entre un número y veinticinco es igual a la mitad de ciento ochenta y cuatro,
disminuido en cuatro.
f,¡nrrntnns
Orden y representación.
Fracciones equivalentes.
Operaciones con números
racionales.
Potenciación y radicación
de fracciones.
Operaciones combinadas
con fracciones.
.l
J,
>:-
Fracciones y expresiones
decimales.
Operaciones con
expresiones decimales.
T, JI
Porcentaje.
Operaciones combinadas.
-.
'.r:r"f.
#:;i
'otv'",; -,--;:-'
*,":
',
11' ¡
.{
Srrulcrór lNtctAl DE ApREr{DtzArE
1. Observen la imagen y resuelvan.
a. Comoleten.
rn et grupo hay
f]
,on varones y
son mujeres.
cuyas respuestas seanocadurrlu O. tas siguientes fracciones.
chicos, donde
b. lnventen preguntas
{-l
f]
9i g;5; g
c. Comparen con sus compañeros las preguntas que realizaron.
MMÑÑMMWI
Orden
y repres€ntación
rc
f,úmeros racionales
Los números racionales son aquellos que se pueden escribir como fracción.
Se denomina fracción al cociente entre dos números naturales a y b (con b distinto de O).
5-)
--)
8
numerador
Quedafiderc*a.
denominador
Toda fracción mayor que un entero se puede expresar como número mixto.
w
U
4 .7
3 '3
t
un entero
3
Representación en [a recta numérica
Para representar fracciones en la recta numérica, se divide cada unidad en tantas partes iguales
como indica el denominador y se toman tantas partes como indica el numerador.
Para representar
]:
a --.)
3
Como el numerador es 3,
se tomon 3 de esos partes.
1z
Como el denominador de lo fracción es 2,
se divide cade unidod en dos partes iguales.
Gomparación de fracciones
Para comparar dos fracciones, se pueden usar distintos procedimientos.
Para comparar
multiplican cruzados los numeradores y denominadores, comenzanv ft
.
f
t.
do por el numerador de la primera fracción. Se escríben los resultados obtenidos y se los
i, Z+ t.6c 4.5+ 6c 20, entonces f e f.
e Para comparar V j, como los numeradores son iguales y en se divide al entero en menos
J
+
compara.
partes que en
.
f,
Para comparar
entonces + > +.
I v f, .oro I
es
reno, que un entero v f es mayor que 1, entonces Ie
1. Respondan y expliquen las respuestas.
a. Para representar f en ta recta numérica, ien cuántas partes se puede dividir la unidad?
b. iCuál de las siguientes fracciones es mayor? I o #
c
iCómo pueden comparar
f
con Jz zv
{
con
lz-
f.
rE
AgfIVIDADES
Orden y representación
1. Representen en ta recta numérica las siguientes fracciones.
a.];
01
l;];l
a.l;l;|;]
01
7.3.2.5
.v416.3.6
2.
{|
Escriban la fracción que representan los puntos indicados con letras.
0ab1c2d3e
,=E
b=E
a:E
,:E
a:E
3. ¡scriban como número mixto las hacciones de la actividad anterior, siempre que sea posible.
.=OE '=OE .:OE ,=OE
d
.=OE
4.
Ordenen de menor a mayor las fracciones que aparecen en el enunciado.
Elvira decidió hacer un pan dulce para compartir con sus nietos. Compró tg O" frutas abrillantaf
das, t<g de pasas de uva, kg ae almendras acarameladar y O. nueces.
f
j
f
d
5. Escriban la fracción que indica la parte pintada. Luego, ordénenlas de mayor a menor.
"+E
'++E .++E
6. Ordenen de menor a mayor las siguientes fracciones y represéntenlas en una recta numérica.
107544215
T'6'6-F't-5'6'9
f
mnB mnmmml
Fracciones eq uivalentes
Dos fracciones son equivalentes cuando representan e[ mismo número racional.
cEi.\f5
Ir-
Para obtener fracciones equivalentes a una dada, se pueden aplicar estos procedimientos.
el numerador y el denominador
número natural distinto de cero.
a\
Se dividen el numerador y el denominador por
un mismo número natural que sea divisor de
los dos.
r'\
24
714
\_/
82
205
\9
es ineducible porque
no se puede simplificar.
t
si dos fracciones son eguivalentes, se puede aplicar la propiedad fundamental de
las proporciones. Si al multiplicar el numerador de la primera fracción por el denominador de la
segunda, se obtiene el mismo resultado que al multiplicar el denominador de la primera por el
numerador de la segunda, las fracciones son equivalentes.
Para verificar
fr ee equivalente
con
ft,
porqu" 15 , 1 6 = 12 . 20 = 24O
Fracción ineducible
Una fracción es ineducible cuando el numerador y el denominador son coprímos, es decir que
solo tienen a 1 como divisor común.
]
ee irreducible Vorque 4 y
7 son coprimoe.
1. Respondan y expliquen las respuestas.
)
a. ZCómo reconocen una fracción irreducible?
b. La fracción irreducible d. ?i, ¿"t?
c. ZCómo se puede comprobar que
;3 V f$ son equivalentes?
d. iCuál es la fracción irreducible ¿.
ÉrrZ
tr
ffJllH?To*".1enres
7.
¡scdban la fracción ineducible que representa cada color, en la siguiente figura.
a
Rojo:
d. Amarino:
3
b. Verde:
B
c fuul:
E
e. Blanco:
E
4
B
8.
Tachen las fracciones que no son equivalentes a la fracción dada.
-2
*7
t4
e'5 -s '
9.
cf; +
72 6 20 10 32
' t7 Z 76 n m
44 76 36 gg
68
55 2l E
d.8 ---+ #
"
56
75
45 90 27 216
1020652
^108307
'57752
6
Escdban como fracción ineducible la parte sombreada de cada figura.
A
B
E
E
E
TD E
E
M
¡.1
ñ
1O. Simplifiquen las siguientes fracciones y exprésenlas como fracción ineducible.
";á=B
o.#=E
lL
e'ff=B
cffi=3
#=E
'i#=E
,á .i,8,;
*ffi:E
n.ffi:f
Completen con una fracción que se encuentre entre las fracciones dadas.
*a'EJ '3
.á,El
ná,8.¿
o-?,8)
,3
'.r,8,+
,'?'!'i
,?,8.3
0,
Operaciones con números racionales
rc
Adición y susüacción
Para sumar o restar dos ftacciones de distinto denominador, se buscan fracciones equivalentes
que tengan el mismo denominador. Para encontrar un denominador común, se busca el múltiplo
común menor entre los denominadores.
2.1 B 5 13
5' 4- 20' 20- 20
=21
46121212
mcm(5;4) = 20
mcm (4:6) =
7
_5
_10 _11
12
)
Los siguientes cálculos se pueden resolver mentalmente.
I entero
son
,v
2
a
*?=Z
2
tonf
enteros
\_-,
^r-+=+
llulüplicación y división
Para mulüplicar dos fracciones, se multiplican los numeradores
zz tzlt
'iru
1
B'4= e-*r= Z
Se
y los denominadores entre
z.3
-z.o -td -1Z --l
5'4=5A=E;
simplificaron
que
multiplicar. tJ'firÍ"i,',ii,i,i"
E- ,^- r^_ --_^_
las ftacciones
se quiere
t------r-___--_--
4
L______________+
3
resultodo.
4
Para calcular una fracción de un entero, se debe multiplicar
sí.
Se simplificí
la ftacción
resultado,
el número por el numerador de la
fracción y dividirlo'por el denominador.
ftae tooo =fr,tooo
="ff/=75o
Toda fracción distinta de cero admite un inverso multiplicativo. Por ejemplo, el inverso multipliaa
. 2, = 1. Para dividir dos fracciones, se multiplica la primera fracción por
cativo de 1
1. porque 3
"t
el inverso multiplicativo de la segunda.
3. 1 _3.12 _a
' 4'12-4'
1 -v
1. Respondan y expliquen las respuestas.
a. iEs cierto que * ? 11r.t
b. Cuando se multiplican dos fracciones, iconviene simplificar antes de hacer el cálculo?
c En el cálculo # , tr,2se pueden simplificar el 15 y el 5?
f
:
rl[
ACTIVIDADES
Operaciones con números racionates
12. Resuelvan mentalmente.
*1*g=E
r.f
e.l+2.:E
-3-?.+:
E
d.?-¿.2=
E
-+:E
ú.
r.1_+=E
13. Marquen con una X el cálculo que representa la situación y resuélvanlo.
Un micro de larga distancia salió de la estación de Retiro rumbo a la costa atlántica. En el camino, realizó varias paradas en las que subieron o bajaron pasajeros. En Retiro subió del pasaje,
en San Clemente subió
del total, en Santa Teresita bajó de los pasaieros y en San Bernardo
f
]
fr
subió
f.
Si el recorrido finalizó en Mar de Ajó, Zqué parte del pasaie llegó?
*?* +o-+.?=
b.
1-?.#-\*?=
"t-(;.#-+.3) =o
ú
14. Resuelvan.
r
a|-1**=
b-1- (+.
E
E
E
E
E
+) =
'?.+-+
d-?-tr**=
e.l-
z*
j:
¡z-P.1)
:3
ú
I
15. Compteten los cálculos.
"+.EJ
16. Escriban (,
d+-!:;
'E -i:i
) o = según conesponda.
a.e+!!t
b.5-?o'
'tr.+!
t
d.7
-?oo
/t
tFl
AcrrvrDADEs
operaciones con números racionales
tU
17. Simplifiquen y resuelvan.
l
I
a.l.#=E
".+.+:
,.6'+:E
d.11
.E
d.
.ro:E
18. Completen las siguientes igualdades.
a.l.
'E 4=i
=5
t:,0
11
.!=+
19. Escriban en lenguaie simbólico y resuelvan.
i
I
a. El doble de ]:
d. Un tercio de
b.
El
e. Un medio de 472:
c
El cuádruple de $:
20.
Lean atentamente
a
triple de f,:
Florencia regaló
aún conserva?
f
93:
f. Tres cuartos de 56:
y resuelvan.
de las 45 figuritas que tenía repetidas. iCuántas regaló en totat? ZQué parte
b. Para [egar a Mar del Plata, Rubén consumió f, del tanque de nafta de su auto. Si el tanque
tiene una capacidad de 52 litros, icuántos litros le quedan aún?
c
Camila gasta
J
de su sueldo en impuestos y f,, .n el alquiler de su departamento. Si su suelicuánto dinero destina para alquiler e impuestos? iQué parte de su sueldo le
do es de $Z AOO,
queda para otros gastos?
21, Resuelvan.
,,?r+€
b.z,+=E
,.#,#=E
d.#,#=E
i
22.
,,
I
Completen con la fracción que verifica la igualdad.
*,8=*
o.?,E=,
"8,+:z
' E'+=1
rn
ACTIV|Dáü't5
OperacioRes con números racionales
23, Resuelvan y completen con
(
)o=segúnconesponda.
.+.3c+'3
¡"?.t Ü+,+
cs,fÜ+'u
d.+.io+,4
24" ¡scriban la letra del enunciado gue conesponde a cada dlculo. Luego, resuélvanlo.
a. Un poste se pintó la mitad de blanco y la tercera parte de azul. iQué parte está pintada?
b. La mitad de una herencia se reparte entre tres personas. iQué parte le corresponde a cada una?
c. Dos amigos recorren un camino en su auto; el primero maneja la mitad del recorrido y el
segundo, una tercera parte. iQué parte aún no recorrieron?
d. Eduardo llenó el tanque de nafta de su auto para salir de viaje. Luego de consumir la mitad
del combustible, cargó nuevamente un tercio de la capacidad del tangue. iQué parte del tanque
tiene nafta?
!,-(+.fl=E ü+.+=E C+,3=El !,-+.+=E
25.
6
Resuelvan las siguientes sltuaciones problemáticas.
a. La mamá de Josefina compró cuatro cajas de veinte bombones cada una. Entre Josefina y su
hermana Micaela comieron una caja V ae otra. ZCuántos bombones quedan?
6
f
ü. En un micro escolar viajan 36 alumnos. Si ] de los alumnos desciende en el barrio de
Saavedra, f, to trace en Belgrano V f en Núñez, Zcuántos alumnos continúan en el micro?
'l
c
fr ae sus libros el lunes, y el martes se
quedan
devolvieron 15, icuántos libros
aún en la biblioteca?
En una biblioteca hay 540 libros. Si se prestaron
rrcnteAIIIYA
Don Prudencio desea plantar 5 variedades de flores, gue en total son 240 plantines: 60 son
jazmines, 18 son fresias, 78 son rosales, 30 son lirios y el resto son orquídeas.
e
iCuántos plantines de orquídeas tiene?
ü. iQué fracción representa cada variedad?
lf
Potsnciación
y radicacién de fracciones
rcü
Potenciacién
=a
La potenciación permite escribir en forma abreviada una multiplicación de factores iguales.
l1\3_-41.1.1_
t1\2 1 1 1
\41 -4 4-16
\4)
1
e)'
4 4-64
(?)"
=,
t3
+{m
r-r-,
El
eector pinlado ocupala novena parI,e del cuadrado.
l1\2 1
l1\2
1 11 1
\3) -3 3-e
LLH
tHARtbrttE
WEqE€SN
Para obtener la potencia de una fracción, se debe calcular
la potencia del numerador y la del denominador.
\abcrto)É
0ilner¿...
l4\2 = 42 16
\B) ó"= g
Radicación
La radicación es la operación inversa a la potenciación.
Para obtener la raíz de una fracción, se debe calcular la
raíz del numerador y la del denominador:
- '[o+ -s
"@
125-.\lzo-5
,ffi =6?orqu"Éf =#
,E
=$?o,qu"(+)"
=+
La potenciación y la radicación de fracciones cumplen las
mismas propiedades gue para los números naturales.
I
En ta página 15
peden repasar
propiedada de
ta potenciación y
tas
l¡ ndicacion.
1. Respondan y expliquen las respuestas.
a ZQué indica el exponente en la potenciación? iY el índice en [a radicación?
b. iEs cierto
q"" (7)' : #?
c. icómo se resuetve
fɡ
II
AcTMDADEs
Potenciaciónyradicación de fracciones
II
26.
Resuelvan las siguientes potencias.
..(+)'=E
27.
,(?)':E
b.(+)':E
¿.(3)':E
ü
Resuelvan las siguientes raíces.
".rffi=
b'lE
tffi=
=
28. fscriban en lenguaje simbólico y
d.\8,
=
resuelvan.
a. La raíz cuadrada de cuarenta y nueve cuartos.
b. El cuadrado de cuatro tercios.
c. La raíz cúbica de ciento veinticinco sesentaicuatroavos.
rl
d. El cubo de cinco sextos.
e. La raíz quinta de un treintaidosavos.
f.
29.
El doble de la raÍz cuarta de un medio de treinta y dos.
Completen los cálculos
.fi:+
"(E)'=* "(E)'=+
30.
oiE=t
(t
Calculen el área de las siguientes figuras.
a.
4
b.
F
I
I
menteACTlVA
Si et área de un cuadrado es ¿"
#m2,
icuál es la longitud de su lado?
lq
=EE
EsSngl
Operaciones combinadas con fracciones
Para resolver una operación combinando las operaciones estud¡adas, pueden seguir estos pasos.
r:r
-G)".^l+.2+l,l=
4-1 .2*7.3=
9'.2-'5',5
{+ 1 +l=
_34
-9
1. Se separa en términos.
2. Se resuelven las potencias y raíces.
3. Se resuelven las multiplicaciones y divisiones.
4. Se resuelven las sumas Y restas.
Existen calculadoras que no respetan la jerar'
quía de las operaciones, es decir, no realizan la
Eñ UnñÍ¡SrS t, W$a)|a¡ lBlEpr LEF'
tñ¡tüIsr r&Éi\crnh uqünücl¡ t ¡ñftiórw
R*r¡til¡t,srqg,
qn k3
s$ñt
t-
m. m bt$ tttt*r¡nes
W¡Énbñ
¡QE
EIIeNE?
separación en términos.
Tengan en cuenta que en los cálculos donde
aparecen paréntesis, primero se resuelven las
operaciones que ellos encierran.
1--l
-l-l
t-l
f-r.
E)".ll&'..
-Z)'+=
1. Se separa en términos.
13 .25 _
l3\2 . -d'-d
2. Se resuelven los cálculos que están dentro de los paréntesis.
9 13.25
3. Se resuelven las potencias y raíces.
E- zb-
I,13_
4. Se resuelven las multiplicaciones y divisiones.
_22
5. Se resuelven las sumas Y restas.
1:
l
-
-
.
_
E-T'
6-
-25
1. Respondan y expliquen las respuestas.
a. ZCuáles son los pasos para realizar un cálculo combinado?
b. iEs ro mismo
c
En el cálculo
(+. ?). á qu. +. + .?
+ # . t,
O" puede simplificar antes de resolver la operación?
I lt
tfJllt'fnfcomb¡nadas
con rracciones
31. Resuelvan las siguientes operaciones combinadas.
".(+.
a-ffi +-Gr:
H.4-É:E
b.(3-*)
(T
-+ il=E
Planteen
.ffi =
rl
r;.f ,E-+=E
32.
".(+.*)'
I
i.?.¡W.Gr:
il
y resuelvan.
a
Eduardo leyó un libro de 840 páginas en 3 días. El primer día, leyó aet tiUro. El segundo día,
la tercera parte del resto. ZQué parte leyó el tercer día? ZCuántas págínas representa?
f
b. Tres amigas repartieron una torta de chocolate. Noelia se quedó con la mitad de la torta y
con la tercera parte del resto. iQué parte le corresponde a Celeste?
c
Belén, ..
[
Un atleta participó en una competencia de ciclismo que se realizó en cuatro etapas.
o Primera etapa: recorrió
$-Oet totat.
. Segunda etapa: recorrió del resto.
¡ Tercera etapa: recorrió las dos terceras partes de lo que llevaba recorrido.
f
iQué parte recorrió en la cuarta etapa?
q
ACNWDADES
Operaciones combinadas con fracciones
y resuelvan las siguientes situaciones.
a En la siguiente figura, abc y noc son triángulos equiláteros. Escriban la expresión que permite
calcular el perímetro del área sombreada.
33.
Planteen
In
b.
En la siguiente figura, el lado del cuadrado efcg mide
]
m y el del cuadrado abcd,
Escriban la expresión que permite calcular el área sombreada.
dCc
a
!lá. Completen
con
(, )
o
=,
-(+)'.(á)'ot
b.L, *+O t
35.
s¡n hacer los cálculos.
.(f)'f '
¿.1*i.rC,
Resuelvan.
. fi',8.#'f :
'\8.+.#-t,#=
b.(3)'-Z
d.T,+-+ i?=E
&'r*Er=
]
m.
I lt
tflX?'lLltcomb¡nadas
36.
con rracciones
Resuelvan.
a.,ffi
".(+. +)',+-,8.+:
b.rE;$.+.W
*1,T.8-ffi=
ü
-+:
".f:9.fffi_r-
6
..
(+
.
i. +) ' Ln.3- flffi
=
,.<84. {m - (+)'=
y resuelvan.
a. La suma entre un cuarto de diez y dos tercios de trece.
37.
ú
Escriban en lenguaie simbólico
b. La diferencia entre las dos quintas partes de quince medios y la décima parte de doce.
6
menteACT|VA
Uno de los lados de una alfombra rectangular mide
lndiquen cuál de las expresiones permite calcular.
J m y el otro, J m aumentado en 2 m.
a. E[ perímetro de la alfombra.
i.2.?+2.1+2
ti.z.|*z-(j*z)
iii.z.f+j+2
n z. (J. f)
iii.
b. El área de la alfombra.
t.|*2.]
(J.
z)
'f
t,
coilTEl{tDOS
E.g.ln.ll.la
38.
Representen en la recta numérica.
43.
Completen cada figura para obtener el
entero conespondiente a cada fracción.
c Un medio.
a. Un tercio.
..1;];l;26
a.t;l;t;]
t
39. Indiquen la fracción ineducible que representan los puntos marcados con letras.
b. Dos séptimos.
0123
d. Tres cuartos.
a
Y
abc
40. Tengan en cuenta el entero e indiquen la
fracción que representa cada figura.
44. Simplifiquen las siguientes
Entero:
fr
"mE
c.
[-T-l
,ffi8
bmE
a.ffi:E
r#:E
0.ffi=E
effi=E
c.ffi=E
*#=E
45.
41. Completen para obtener fracciones equiva-
Resuelvan. Escriban el resultado como frac-
ción ineducible.
lentes.
6gEB
b.#:
B B ts a
a.
''42.
$:
105_
315
E ts E ts
Escdban la ftacción ineducible que corres-
ffi
ponde a la parte sombreada de cada figura.
"A
d.
n
fracciones.
^-?.tn-+-+=
_
- 49 -t47
L'32t
76 -
46.
,20 32 25
-'16 15 8
e' 56L56
1s'74'5=
.t5 21 50
" f6' 20' 14
Ordenen de menor a mayor los resultados
de la actividad anterior.
47. escriban en lenguaje simbólico y resuelvan.
a. El triple de la raíz cuadrada de dieciséis
novenos.
b. La raíz cúbica de la mitad de cincuenta y
cuatro.
c El producto entre un medio y dos quintos.
d. El cociente entre d¡ez novenos y diez tercios.
e. La mitad de la suma entre dos tercios y
cinco cuartos.
f. El cuadrado de siete quintos, más uno.
Cuno:-
Fecha:-/-
48.
Lean atentamente
y resuelvan.
a
Anabella tiene 108 fotos que se tomó con
sus amigas. La cuarta parte las tiene pegadas
ciones.
a
en un mural en su pared, la mitad las colocó
en un álbum y el resto, las quiere guardar en
una caja. ZQué parte de las fotos piensa guardar? ZCuántas fotos tiene pegadas en el
El área y el perímetro del siguiente rectángulo.
Z.
)
mural?
b. iCuát es el perímetro de un cuadrado, si se
sabe que su área es de
cmr?
c. Adriana tiene un sueldo de $6 360; destina Rara el alquiler de su departamento,
á puru impuestos, la tercera parte para distintos gastos del mes y e[ resto ]o ahorra.
ffi
I
r
51. Planteen y resuelvan las siguientes situa-
b. El área sombreada sabiendo que abcd y
efcg son cuadrados, ;5'=
f m y -t: + .á8.
dgc
E
ZQué parte ahorra del sueldo?
49.
".
ab
Resuelvan.
\8.[(3)', . g]-
'9
:
c
1-(+)'.3'+*1ff=
".[+,9. h +-+. (3.?)]=
b.
E[ perímetro de la siguiente figura sabiendo
que abce es un cuadrado, cde es un triángulo
equiláteron;5:+:
n\F--''(+.#).2=
5O. Resuelvan.
a. Al casamiento de Graciela asistieron 60 invitados, entre adultos, jóvenes y niños. Si hay
] de adultos y 20 jóvenes, Zcuántos niños
hay en la reunión?
b. Nicolás tenÍa ahorrados $+32. Destinó la
mitad para comprar una bici, la cuarta parte
para comprar un videojuego para la computadora, la sexta parte para un libro V
Oara hacerle
un regalo a su hermana menor. iCuánto dinero
gastó en cada compra?
$
d. El área sombreada, si abcd es un rectángulo,á6=
, rt=f,cm.
dec
3r
c
En el cumpleaños de Rodrigo, su mamá
cortó [a torta en 16 porciones. Si su amígo
Juan come
Mariana
$ Ae U torta, su hermana
fr v Rodriso f,, Zcuántas porciones
sobraron?
d.
La cuarta parte de un edificio está compuesta por departamentos de un ambiente,
las dos terceras partes por departamentos de
dos ambientes y el resto de tres ambientes.
Si en total son 48 departamentos, Zcuántos
de cada tipo
hay?
,:2. Escriban en lenguaje coloquial y resuelvan.
a.
3t
8'6' :
b.
-3..10_
5'3-
"lFJ=
d.Z'tE
=
mEmmmmEH
Fracciones
y expresiones decimales
Una fracción representa una relación entre dos cantidades.
Aquelina quiere pintrar las paredes de su caea. Tara lograr el color que le gusta, mezcló dos
?oLee rqoo con cinco amarillos . ¿Cuál es la fracción que re?reoenta la relación eníre los potne
roJosy amarillos?
Lafracciónf;inaica que cada dos potee roios se deben utilizar cínco amarillos.
Si se efectúa la división entre el numerador y el denominador de una fracción, el cociente que
se obtiene es la expresión decimal de la fracción, que está formada por una parte entera y una parte
decimal.
ñ=
O,U "clnco
décimos" &
= O,O5 "ctnca centésimos'
&
=O,OO5 "cinco miléstmos"
El denominador de una fracción decimal tiene tantos ceros como lugares decimales tiene la
expresión decimal que le corresponde
Una fracción irreducible tiene una expresión decimal ftnita, cuando los factores primos del denominador son potencias de 2, de 5 o de ambos.
3_15_¡d
Z- 10- t'r
*m
&=ffi=o,32
=0125
Existen fracciones que no se pueden escribir como fracción decimal y por lo tanto, no tienen una
expresión decimal fi nita.
$ no üene unafracción decimal equivalenfn, porque uno de sus factores primos (elI)) no es
potencia de 2 ni de 5. ?or lo fnnln, eu una expresión decimal periódica.
$
3
= Z t 9 = 0,222... =
O,2
---+
Se puede segutr dividtendo lnfinttomente.
La expreslón tlene lnflnitas clfnis declmales perfódlcas.
1. Respondan y expliquen las respuestas.
a. iCómo se obtiene la expresión decimal de una fracción?
b. La expresión 2,10, ise lee dos enteros diez décimo.s o dos enteros diez centésimos?
c. ZQué estrategia pueden utilizar para decidir si la expresión decimal correspondiente aS
es finita o periódica (sin hacer la división)?
Curso:
Fecha:
rll
53.
ACTIVIDADES
Escriban la expresión decimal que corresponde a cada fracción.
c$=
+:
b. +:
a.
54.
y expresiones decimales
Fracciones
a.f,=
1_
Escriban la fracción que conesponde a cada expresión decimal.
Completen con
(, )
o
otll o?
b. 0,24[-l o,rot
a.
a.
b.
57.
Marquen con una
X
=
d.0,23:
r
según conesponda.
d.
0,230
g. 1,03
o2
,?
r. 1,030t,,
e. 2,777
"of!3
56.
9
h. 20
".0,r=[J b.0,14:E "r,r=!
55.
t:
g.
".I =
t.j=
O
n. o?
i.
[-l
t,or
O;
f [-l o,or
las fracciones decimales.
#D
áo
..¿c
e.
d.;eo
f.
áo
'.#C
n.áo
3c
Completen con una expresión decimal que se encuentre entre los números dados.
a.
L,5
7,7
b.
1,5
7,6
c. 0,09
0,9
d.
7,5
1,05
e.7,r2Dto
f.0,83D o,g¡
[-]
h. 0,68D
g. 0,83
o,e¡
o,ut
58. Resuelvan.
a. Escriban dos cuentas de dividir entre números naturales que den como resultado
0,2.
b. Escriban dos cuentas de dividir entre números naturales que den como resultado7,75.
59. Completen la tabta.
W # #M EgEl
Opemciones con expresiones decimales. Porcentaje
E[ resultado de multiplicar dos expresiones decimales finitas tiene tantos lugares decimales como
la suma de los lugares decimales de los factores.
Cuando se multiplica una expresión decimal por 10, 100, 1000, etc., se corre la coma a [a derecha tantos lugares como ceros tenga e[ 10,100,1000, etc.
1,21
.10=ffi.io=ff=tz,l
Para realizar ta división decimal, se debe multiplicar el dividendo y el divisor por 10, 100, 1000,
para que el divisor sea un número natural.
22,8 :4,12
43,25 : 1,5
ü.',: J.'o
15
J.roo J.roo
432,5
22BO
: 412
Cuando se divide una expresión decimal por 10, 100, 1000, etc., se corre [a coma a [a izquierda
tantos lugares como ceros tenga L0, 100, 1000, etc.
En ta
Para calcular la potencia o raíz de una expresión decimal, se puede escribir
la forma fraccionaria de la expresión y luego, se resuelve la operación.
o,7z=(+)'=ffi=o,+e
I
,fqos=ffi=#=o,t
pár$¡e41
peenqw
úno¡erccnhrc
bpaqri¡rfhy
hrffirde
ffirs.
Porcentaie
Un porcentaje indica la proporción de un entero. Para comprender cómo se obtiene un porcentaje se puede tener en cuenta e[ siguiente ejemplo:
2B%dezoo
=ffi.zoo
=?#=
B4
Aproximación
Para aproximar por redondeo a una cifra decimal determinada hay que observar [a cifra decimal
síguiente:
o Si es mayor o igual que 5, se suma uno a la cifla
o Si es menor que 5, la cifra considerada
se
considenda y se eliminan el resto de las cifras.
deja igual y se eliminan el resto de las ciftas.
O,27 aVroximado aloe décimoe esO,3
O,24 aproximado alos décimos es O,2
1. Respondan y expliquen las respuestas.
a. iQué estrategia se puede utilizar para multiplicar 5,24 . 0,3?
b. En el cálculo 5 : 7,2, iconviene multiplicar ambos números por cien?
c El73o/o de 1690, Zes lo mismo que 0,13 . 1690?
L
I I t+
60.
tf.'N.tfirtcon
expresiones decimares. porcentaie
Resuelvan los siguientes cálculos.
a. 6,25 + 8,73 =
Í.
f:::]
10,28 =
f-]
7g,7g
h.3,2t+4-6,77:t-]
f-l
d,75,097+3,809=f::-]
e.7 - 4,5!g
-
g. 20,08 -
b.5+3,807=
c.39,06 + 75,4\=
72,07
.. 8,72 + 3,75 - 7,07
:[::]
l. 77,03 - 8,25 - 7,7 =t-l
=f-l
61. Planteen y resuelvan.
a. Natalia compró una remera de $t25,30 y unas botas de $339,90. iCuánto gastó en total?
b. Pablo fue al supermercado con $879,50 y gastó $6Q7,45 en sus compras del mes. iCuánto
[e
sobró?
c. Marina tenía ahorrados $579,35, su madrina le regaló $t37,zo y luego gastó $308,75 en un
par de lentes. iCuánto dinero tiene ahorrado aún?
d. Ana Clara fue al shopping y gastó $739,99 en una remera, $150,50 en un short
V $205,30 en
una bikini. Si llevó $500,70, icuánto dinero le sobró?
e. En una carnicer-r,a, el kilogramo de lomo cuesta $75,10. Si Claudio compró 2 kilogramos y
medio, icuánto dinero gastó?
62. Escriban
como expresiones decimales y resuelvan.
a.10,2+]=
d.l*3,46-]u=
-+ =
cf-0,75:
e.22,7-l-z:
b.7,38s
Í.
6,23
- (+. t) =
ASTIVIDADES
Operaciones con expres¡ones decimales. Porcentaie
63. nodeen con color la respuesta corecta, sin hacer la cuenta.
L
.0,2
3,5
:
o,o7
b. 13.0,3=
c. o,o4 . 0,5 =
64.
b. 0,015 .0,2
L7,5
0,3913,910,039
0,002
:
.2:
d. 0,15 .0,2 :
e. 0,15 . O,O2 :
f. o,t5 .2 :
:
:
9.4,8 :,2,4 :
h. 0,48 i 2,\ =
¡. 0,048 :24 :
¡. 0,48 :0,24 :
k 0,048 : 0,2\
l. 0,048 :2,4 :
.3
o 0r3
'
.
0,03
0,003
o,o4l o,4l
4
0,41 4
0,32
I
I O,O4
3,21 0,032
.2
t
t
.
:
Completen las tablas.
o,43
:
c. 0,15 :
d.7,1, :
b.7,9'
Q.0,71
:
f.2,9, =
67.
f.9,6 : 3 :
lo,o2lo,2
66. ¡scriban cada número como fracción y
a.
d. r,2 z 0,3
e. 0,6 : 1,5
o,7 17
Unan con una flecha cada cálculo con su resultado.
?-7,5.0,2:
65.
I
Escriban en lenguaje simbólico
resuelvan.
g. {0,^81 =
h. {0,027
l.
{t,25
i..'t¡@
:
:
:
k. {/0O016 =
r.
lo34t:
y resuelvan. Expresen el resultado como fracción y como
erpresión decimal.
a. La diferencia entre [a cuarta parte de 128 y el cuadrado de 2,5.
b. La suma entre la tercera parte de 106,5 y [a raíz cuadrada de
Curso:-
1.,44.
Fecha:-/-
l-
Or2
0,02
0,002
I I Lf
68.
t
tflIll'f3trcon expresiones
Calculen mentalmente los siguientes porcentaies.
2oo/ode
100:
f
: f-l
t 25o/ode 80 : f-l
b. s'olo de z0
69.
t
decimates. porcentaie
I
d.1oolo de 200 =
e.10% de 50 =
f.3orode
100
f:J
*3oYode 1000 =
t-l
h. 5% de tro
:f
-
I
i.
3olo
f-l
:D
de too =
D
Resuelvan los siguientes porcentaies.
:
e.
55o/o
b.10% de 580 =
f.
42o/o
I
9,.730o/o de 500
4o/" de 720
260/" de 2 000 =
d.70"/o de 130
:
de 7 000 =
de 300
:
:
h.775o/o de 4oo =
70. Resuelvan las siguientes situaciones y redondeen el resultado a los centésimos, si es necesario.
¡.
Daniela compró una licuadora que costaba $355,5. Como abonó en efectivo, le hicieron un
descuento del 20%. ZCUánto pagó por la licuadora?
b. Sitvia compró la misma licuadora que Daniela, pero como abonó con tarieta de crédito, le
recargaron un 160/o. iCuánto pagó Silvia?
c. A una fiesta de egresados asistieron 160 personas. E|25"/" de los asistentes era de otras
escuelas y de los restantes, el 15olo eran los alumnos organizadores. ZCUántos chicos de otras
escuelas asistieron a la fiesta? iCuántos chicos la organizaron?
F
menreACflvA
| ,. librero uur.ntO un 25o/oe[ precio de una nove]a que costaba $tto. Una semana después se
I la vende a un amigo al mismo precio que tenía antes del aumento; idebió descontar un 25o/o al
nuevo precio para ltegar at mismo costo que tenía el [ibro?
I
l(
#MK#HgEEI
Operaciones combinadas
Para resolver una operación donde intervienen fracciones
las operaciones estudiadas, pueden seguir estos pasos:
2,5
tu+
O,42,+-^[036
=
25.4-14\2.3
_^[_?9__
10 5 ' \10) ', 10 1100 25 4.16 3 6
10'b* 1oo: io-1ó=
2.16 6 3
3' 30 10- 5
y expresiones decimales combinando
1. Se separa en términos.
2. Se pasan las expresiones decimales a fracción.
3. Se resuelven las potencias y raÍces.
4. Se resuelven las multiplicaciones y divisiones. Luego las
sumas
y restas, y se simplifica.
Si en el cálculo aparecen paréntesis, primero se resuelven las operaciones que ellos encierran.
f-------------1
2 1z.
É)
- ^n,21
=
3.(12,5\_"@__
2 \10 ' 5) 1100 z 1B y100
nz1
2 10
1. Se separa en términos.
2. Se convierten las expresiones decimales a fracción.
3. Se resuelven los paréntesis.
3,18 _11
4. Se resuelven las potencias y raíces.
27 _11 _O
5. Se resuelven las multiplicaciones y divisiones. Luego las
sumas y restas, y se simplifica.
210
10 =
10105
En algunos casos, es posible aplicar la propiedad distributiva para suprimir los paréntesis.
,,u
- (Z)'
5.(3_4\_(3\2_
(2 + o,B)
2 \2' 5) \2) 5 3.5 4 t3\2
2'Z*Z'5- \Z) =
53.54I
22'25
415.20
I
7
4 * 10-4=z
=
1. Se separa en términos.
2. 5e convierten las expresiones decimales a fracción.
3. Se aplica la propiedad distributiva.
4. Se resuelven las potencias y raíces.
5. Se resuelven las multiplicaciones y divisiones. Luego las
sumas y restas, y se simplifica.
1. Respondan y expliquen las respuestas.
a. ZCómo se resuelve un cálculo combinado que incluye fracciones y expresiones decimales?
b. ZCómo se resuetve lE. O,nZ
rls
A TMDADES
Operaciones combinadas
71. Coloquen ),
a. {/o,oo8
( o = según conesponda.
.t[
b.r,22-t!
72.
- +)' =
lm.o,r
c. 7,32 -
d.
7,r2-7
r
c. z .
^[o,e+! r . i/o¡64
d. 0,043 * o,r
[-)
0,42 +
e. i/0,00032
o,r
0,23
7,72
s. l0F00T :
fi + 7,2 -+ '? =
=
h.(+.
t)',",pn.?-#=
=
¡.
+ 3,2
-,8 :
i. (\E
e.J*{075-0,52:
f. lop-5 + 0-"0-75
l19t
.t. #:
-
+ 0,5')
(0,1,
z
* {Op4)
7,6e +
=
f.:
rc(Oaa.iE-t),*=
1.
({OFT
*
f-\
[
f. (0,1 + o,o3),
Resuelvan los siguientes cálculos.
a. (o,ez
b.
4[0,027 +
'[6-Jir)'
't
+ 0,72 =
._
1i10,0016
[-l t,l,
CONTENIDOS
NTEEHAf,I¡N
l3'll+.lS
73. Ubiquen los siguientes números en una
rccta numérica.
".(''.0,0) E:¿
t; 0,4; 7,2; ] ; 2
b.]; t3; z3;l; t
a.
74.
Escriban cada fracción como expresión
decimal. Luego, ordenen de mayor a menor las
expresiones obtenidas.
a.$
b.?
d.i
c.fr
75. Marquen con una X tas fracciones decimales.
..¿o
f.To
b.#ddO
s.iio
'+c
d.&o
..áo
_
{0,64
r-\
L J0,64
n.+o
1.#o
i';tO
O+
c iF,oor O (rt)'
d.ffio(+)'
b.
{r,56
e.3,52o+
r.
{op4
s.7?
rr.
!
!
O
+
lr,r,
o,a
¡.(t)'o(;)'
i.(?)'c\F
77. Resuelvan los siguientes cálculos combinados.
a.0,252 + 0,52 - 10,008 =
b.iE-0,25:2+ffi=
,
E)',+0,5:!
79. tean atentamente y
cuesta $s8,40.
Cliente 1: compró 5 kitos.
Cliente 2: compró 2,5 kilos.
Cliente 3: compró 7,5 kilos.
iCuánto pagó cada cliente por su compra?
. Si al comprar más de 4 kilos se realizara un
descuento de[ 10%, Zcuánto deber'r,a pagar
cada cliente?
b. Un pastelero compró 121. kg de chocolate a
$65,5 el kilo para elaborar bombones.
. iCuánto pagó por el chocolate que compró?
.
Si el kilo de bombones cuesta $82, ¿cuántos kilos de bombones necesita vender para
recuperar e[ dinero invertido?
80.
Calculen e[ perímetro de las siguientes
figuras.
a.b
áb- : 3,85 cm
b-c : 5,25 cm
I
:r
a
\E - (É . r,r)' =
d.0,2+ 18.3=
e. ldFr5rTFl2.Z-tr=
f.(iF+0,5,) :!5-1:
c 0,32.
s. (\ñF4 * r/0,09)'- (o,t .
resuelvan.
a. En una heladería, un kilogramo de helado
76. Completen con ), ( o = según conesponda.
a.
78. gscdban e[ número que verifica el oálculo.
b.
ñ:2,75
cm
b
+
Lr)
=
C.
áE
:
4,08
cm
ac=+.abcm
"4.
85.
81. Respondan.
a. Sabrina multiplicó un número por 10, luego
lo dividió por 13 y el resultado que obtuvo
fue f. iCuál es el número?
b. A otro número to dividió por 100, [e sumó
50,5 y obtuvo 100. iDe qué número se trata?
Lean atentamente
cálculo que permite resolyer el problema.
En el año 2005, una escuela tenía 600 alumnos en su matrícula. Si en el 2013 la matrícula
aumentó en un 15olo, icuántos alumnos tiene
ese año?
a. 600 .
82. Completen la tabla.
y marquen con una X el
1,15
b.600+600.$:roof.l
c 600.15 :100
d. 600 . 0,85
86.
Respondan.
a. El
4Oo/o
de una cant¡dad es 1 500. iCuál
es
esa cantidad?
b.El75"/" de cierta cantidad es 6000. iDe
83.
Resuelvan.
a
Antes de llegar a su destino, un avión realizó dos escalas. En la primera descendieron
35 personas, en la segunda 50 y 775 llegaron
al destino final. iQué porcentaje descendió en
cada escala? ZY en el lugar de destino?
b. En un curso de 36 alumnos, 3 no asistieron el lunes a la escuela, iqué porcentaje de
asistencia hubo ese día?
c Si durante el mes de abril llovió 6 días,
icuál es el porcentaje de días de lluvia?
qüé cantidad se trata?
c. 5i el 725"/" de una cantidad es 120, icuál
es esa cantidad? LY su 25o/o?
d. El2OYo de cierta cantidad aumentada en
75 es 29. iCuál es esa cantidad?
e. El30% de cierta cantidad, disminuido en 26
es igual a 22. LCUá| es esa cantidad?
f. El 50% de una cantidad, multiplicado por 3
es 141. iCuál es esa cantidad?
87. verifiquen que a todos los precios se les
haya realizado un 20% de descuento. Coniian
los precios inconectos.
d. Un equipo de música se vendió con un
!2o/o de descuento a $t331,6o. iCuál es el
precio sin descuento?
e. En un recital, se vendieron 624 entradas
de un total de 780. iQué porcentaje de entradas quedó sin vender?
84.
Calculen mentalmente.
a.7Oo/o de 140.
b.7OVo de 55.
c
d.
20"/" de 90.
2oo/o
de 300.
e.25o/o de 1000.
f.25Y" de 80.
g. 5Úo/o de 88.
h.50% de 1350.
i.75o/o de 100.
i. 75"/" de 1200.
k 75Oo/o de 64.
L 150o/o de 1300.
88.
Resuelvan los calculos combinados.
a.7o"/o de $sao + 3.5o/o de $rze
b. 772"/o de $53 50% de $47 =
c
:
-
36"A de $54 +
:
de $+g
d. 75o/o de $81 + 9Oo/o de $142 =
e. 32o/o de $6s - 72"/" de $73 =
2Oo/o
AuroEvALUAclón¡
89.
a.
90.
Representen en la recta numérica.
t;
{r;0,5; oJ;
o,7s
tE=r---r E=T
y la otpresión decimal que corresponde en cada caso.
Escriban la fracción ineducible
'^4,
9t Escriban en lenguaje simbólico y resuelvan.
a La suma entre la raíz cuadrada de 0,64 y el cuadrado de ].
E
E
E
E
b. La diferencia entre la raíz cuadrada de &, l^ raíz c(tbica ¿" &.
c
El cociente entre [a suma de 0,5 V f, V la raíz cuadrada de
d. Et producto entre la suma ae I
92.
a
Lean atentamente
V
t,u
t.
ffi.
raíz cuadrada de 2,56.
y resuetvan.
En la libreria "Pitágoras" se vendieron 120 novelas románticas durante el mes de marzo. En
y en mayo, aumentó un
marzo. iCuántas novelas se vendieron durante los meses de abril y mayo?
abril, la venta de esas novelas disminuyó un
75o/o
25o/o respecto de
b. En la misma tibreria hay un estante con libros de Matemática, Flsica y Biología. Los libros de
Matemática son 32 y los de Física son 16; entre ambos representan el 60% del total de los libros
del estante. iCuántos libros hay en el estante? ZCuántos son de Biología?
93.
Resuelvan los cálculos combinados.
" ffi:+
* ,[t a),75
-
(t
- 1)' =
b.3 ,F* + t[¡4
z 0,42
-(+)'=
E
f,snrrnronr
16. Gráficos y tablas.
17. Funciones.
18, Función de
proporcionalidad directa.
13. Función de
proporcionalidad inversa.
S¡ru¡cló¡r lilrc¡Al DE ApREf{DrzAlE
1. observen la escena y respondan.
a. iDe qué depende [a cantidad de personas que podemos encontrar en cada puesto?
b. Si una persona tiene $50 para comprar naranjas, Zde qué depende la cantidad que puede comprar?
c. Si solo se vende fruta por kilogramo y una señora gastó $36 en manzanas, Zdónde compró?
d. ZCuántos kilos de cada fruta compró una persona que gastó $39 en "Lo de Fermín"? Pueden
ayudarse armando una tabla donde registren los precios de cada fruta según [a cantidad.
e. Modifiquen las situaciones anteriores para que tengan una única solución. Luego, respóndanlas.
MNffiHHHHHI
Gráficos
tablas
Un sistema de ejes cartesianos está formado por dos rectas perpendiculares que se cortan en un
punto llamado origen de coordenadas.
La recta horizontal se denomina eje de abscisas (eje x) y la vertical, eje de ordenadas (eje y).
Cada punto queda determinado por un par ordenado de valores, donde el prímero representa la
abscisa y el segundo, [a ordenada.
v
5
v
250
4
200
3
150
2
100
7
50
72345x
12345x
s = (O:O) ee el orígen de coordenadas
a=(1:1) 6=(2;O)
6=(O;4)
p=
(1:150)
q= (5;2OO)
Los gráficos permiten leer con mayor hcilidad los
datos de una situación. El siguiente gráfico muestra la
o
2 20
u
variación de la temperatura a través de las horas.
o En el eje x se representó el tiempo (expresado en
horas) y en el eje ¡ la temperatura (en oC).
e A las 13 horas se registró la mayor temperatura
18
c
f T6
F
e 74
U
G
E 72
u
F
Para representar
estos puntos
conviene tomar
unidades distintas
en cada eje.
10
y a las 10 horas, la menor.
o Entre las 10 horas y las 13 horas la temperatura
aumentó y, luego, empezó a descender.
o Entre las 16 horas y las 77 horas [a temperatura
8
6
4
2
10 77 72 73 74 75 76
rr¡mpo
(Er.r
77
se mantuvo constante.
non¡s)
Los datos del gráfico se pueden traducir a una tabla como la siguiente.
1. Respondan y expliquen las respuestas.
a. iEs posible representar un punto a sabiendo que su abscisa es x :
b. aSe pueden usar diferentes escalas para cada eje de coordenadas?
c El punto s = (2;3), icoincide con el punto b = (J;2)?
3?
rlE
ACTIVIDADES
Gráficos
y tabtas
1. Representen los puntos en el sistema de eies cartesianos.
= (3;1)
6 = (2;3)
¿
c:
I
(6;7)
d = (7;0)
e = (o;9)
f=
s:
(0;0)
(9;5)
h : (5;10)
i : (1;6)
0
2. Escriban
(
las coordenadas de cada uno de los puntos representados en el gráfico.
d
c
ct-
b:
d:
g=
b
0
3. Representen
(oü)
I
.:(oo)
e
a
oo)
(Do)
oü)
los datos de la tabla en e[ sistema de eies cartesianos.
(
(
0
lE t#."'#H',,,
4.
)
completen con el par ordenado que cumple con lo indicado y luego, representen.
a
La ordenada es 5
b.
La abscisa es 4 y su ordenada, el doble.
c
Un punto que se encuentre sobre el eje de
y la abscisa,
Z.
.=(cü)
o=oc)
ordenadas y otro, sobre el eje de abscisas.
d.
.:(c'[])
a:OO)
La abscisa vale la mitad que la ordenada.
.=oo)
e. El punto que cumple la condición anterior
sty-5.
0
)
'=oo)
Observen el gÉfico y resuelvan.
a. Completen la tabla.
5.
z
F
&
r
)
o
I
F
qué hora la temperatura fue de 12
oC?
b.
aA
c
aA qué hora se registró la temperatura
máxima? ZCuál fue dicha temperatura?
0
ro
iN
il
)
6.
Observen el gráfico
y respondan.
Clara fue desde su casa al parque en bicicleta, tomó un
refresco y regresó. El gráfico representa la distancía desde la
casa de Clara al parque a medida que transcurrió eltiempo.
a iCuántos minutos...
r ... tardó en llegar al parque?
.
... estuvo en el parque?
r ... tardó en regresar
a su casa?
'tto
z
I
I
6
\
I
b. iTardó más para ir al parque o para volver? Expliquen
la respuesta.
\
z
I
rd
o
TI
""1
r_E
(Et
MI
t
TIE
ACTIVIDADES
Gráficos y tablas
7. lean¿tentamente y
respondan.
Para controla¡ el sano crecimiento de su perra lndia, Abigail decidió anotar su peso durante 360 días.
a. iCuánto pesaba lndia al nacer?
1;
b. ZCuántos días tenía lndia cuando pesaba 3 kg?
z
o
o
c. iCuál era e[ peso de la perra a los cua-
tro meses?
d. iEn algún período la perra mantuvo un
0
01
02
ot
0
0i
peso constante? En caso de ser afirmativo, indiquen en qué período.
0
0
\EN
Observen y respondan.
Una empresa registró mediante el siguiente gráfico sus ingresos de los últimos 1.8 meses.
8.
u
d
rJ
z
|¡
o
u
z
0
ts5
a. Transcriban en la siguiente tabla los ingresos de [a empresa en ]os seis últimos meses.
b. iEn qué mes se registró el mayor ingreso? iY e[ menor?
ZEn qué momento
del año los ingresos de la empresa descienden?
Completen
la tabla, sabiendo que en los cuatro meses siguientes, las ganancias de la empred.
sa aumentaron $Z SOO por mes.
c.
e. Continúen el gráfico con los datos obtenidos en el punto anterior.
f. Si en los meses 23 y 24 se registró un ingreso de $ZZ 500 cada mes, iel ingreso aumentó
disminuyó con respecto a[ mes 22? Representen estos datos en la gráfica.
o
ffiMHHHHHHI
Funciones
Cada una de las siguíentes gráficas representa una relación entre dos variables.
a
zU
o
U
g
É
I
)
72145x
200 300 400
x
CANnDAD oe ¡nmón (eH e)
En el grófico se relaciona la cantidad de paquetes de solchichas con su precio. Los puntos opare-
cen oislados porque se usan contidades enteras
(no se fraccíonan).
En el grdfico se relaciona la cantidod de jamón
con su precio. EI gráfico estó formodo por uno
líneo recta porque el jamón se puede vender en
d¡stintas cantidades.
Los dos gráficos corresponden a relaciones que son funciones.
)
Una relacíón es función cuando para todo vator representado sobre el eje x te corresponde un
valor representado sobre et eje
¡
únio
tF R NciartE6l
$KE, DR euub, ?AF[ CAq,uR EL REab
IE muÉB !É $aollfiiB,O qEñb6 !É fAl6rt-.
iQÉ IIüERESAñÉ Et EuAE'
Para una determinada cantidad (variable
independiente) existe un único precio. (variable
dependiente). Se dice que el precio depende
de la cantidad o que el precio está en función
qE w AEIÉr,lr ttttf,E
A€íA(E á¡FBA TbTB
ru&
Bieelg6ÑI¡g$R-
de la cantidad.
1. Respondan y expliquen las respuestas.
a. Si un mismo valor de x tiene tres valores de y distintos, ise puede decir que es función?
b. Si a cada valor de la variable independiente le corresponde por lo menos un valor de la
variable dependiente, ies función?
c. iEl gráfico de una recta siempre es función?
d. La variable independiente,
Zse representa en el eje horizontal?
r17
ACTlvlDADES
Funciones
9. Escriban tres ejemplos
de relaciones que sean función.
10. Marquen una X en los grráficos que corresponden a funciones. Expliquen la respuesta.
a.ce.
(
11. Resuelvan.
a
Completen la tabla teniendo en cuenta la medida del lado de un pentágono regular y su perímetro.
(
b. Representen la información de la tabla en un sistema de ejes cartesianos.
(
c. iEs correcto unir los puntos del gráfico anterior? ZPor qué?
d. La relación entre los lados de un pentágono regular y su perímetro,
Zes función?
iPor qué?
(
ffiHHHHNHHI
Función de proporcionalidad dirccta
Dos variables son directamente proporcionales cuando el cociente entre las cantidades es constante.
El número que se obtiene al dividir las cantidades se denomina constante de proporcionalidad (k).
El perímetro de un cuadrado es directamente proporcional a la medida del lado.
)
4:1=4
k*4
B:2=4
(constante de proporclonaltdaQ
. Lenguaie coloquiaL el cociente entre dos cantidades
. Lenguaie simbólico: y : x :4, entonces y : 4 . x
correspondientes es igual a 4.
fórmulo de la funclñn
)
eu
zU
o
É
F
U
E
É
U
I
La representación gráfica de cantidades directamente proporcionales da como resultado un conjun-
to de puntos alineados sobre una recta que pasa por
el origen de coordenadas.
)
1. Respondan y expliquen sus respuestas.
a. Si las dos variables aumentan o disminuyen, rse puede decir que son directamente proporcionales?
b. En una relación de proporcionalidad directa, si una variable aumenta e[ doble, icuánto
)
debe aumentar la otra?
Si se muttiplica por ] ta variable independiente, Zpor cuánto se debe muttiplicar la variable
dependiente para que se mantenga una relación de proporcionalidad directa?
d. A partir de los datos de una tabla, Zcómo se puede identificar si se trata de una relación
de proporcionalidad directa?
c
rlE
ACTlvlDADES
Función de proporcionalidad directa
12. Escriban tres eiemplos de que sean directamente proporcionales.
(
13. Marquen con una X las relaciones que son directamente proporcionales.
2
4
6
..c
b.c
".o
5
7
9
3
7
10
d.o
5
5
2
30
75
10
4
40
20
76
6
10
72
28
40
14. Resuelvan.
a. Completen la tabla para que las variables se relacionen en forma directamente proporcional.
Luego, representen tos puntos en un sistema de eies cartesianos'
b. iCuál es [a constante de proporcionalidad?
15. observen el g¡áfico Y resPondan.
El siguiente gráfico representa el precio de
un postre helado según su Peso.
.
a
Completen [a tabla.
v
b. Las variables, ise relacionan de forma
directamente proporcional? ZCUáI es la
constante de proporcionalidad?
0
HHHHmHHHT
-
Función de proporcionalidad inversa
Dos variables se relacionan de forma invesamente pruporcional cuando el producto entre los valores
que se conesponden es constante. A ese producto se lo denomina constante de proporcionalidad (k).
En la eiquienÍe t abla se regietraron algunos valores que corres?onden a la base y la altrura de
rectrángulos de
24
cmz de área,
2.12=24
3.8=24
4.6=24
€U
zU
:É
F
J
k:24
(constonte de proporcionalidad)
El producto entre dos cantidades correspondientes es
igual a 24.
x.Y:24,entoncesV=+.
Cuando los valores de una variable aumentan, los de
la otra.variable disminuyen en [a misma proporción.
La representación gráfica de variables inversamente
proporcionales da como resultado una curya denominada
hipérbola.
)
1. Respondan y expliquen las respuestas.
a. En una relación de proporcionalidad inversa, si una variable aumenta aI doble, iqué sucede con la otra?
b. En el gráfico de una función de proporcionalidad inversa, Zlos puntos están alineados?
c. Si en una función, una variable aumenta y la otra disminuye, ise puede decir que las
variables son inversamente proporcionales?
d. Si et producto entre la varíable dependiente y [a independiente es cero, ae puede decir
que se trata de una relación inversamente proporcional?
I I5
?fl:Ylt-tt-Troporcionaridad inversa
16. Escriban tres relaciones que sean inversamente proporcionales.
(
17. Marquen con una X las tablas gue corresponden a funciones de proporcionalidad inversa y
hatlen ta constante de proporcionalidad. Luego, representen los datos de esas tablas en un siste'
ma de eies cartesianos.
b.n
".n
"n
.".i?
-i{!
lltr."¡: la
r::4T*F
d.D
iri::ffi:Eryi
,
1
3
2
15
2
63
4
6
3
7
3
10
3
42
7
4
75
5
5
6
9
74
10
2
'fi-';
I
I
(
l&
Lean atentamente
y resPondan.
Laura está organiZando un festival de danzas árabes. Para ello, alquiló una sala en el compleio
cultural plaza. Como los gastos a cubrir por el alquiter del lugar son de $gOOO, deberá cobrar la
entrada en función de la cantidad de butacas que pueda ubicar en la sala.
a Completen la tabla.
h
Las variables,
&e relacionan en forma inversamente proporciona[? Si es así, escriban la cons-
tante de proporcionalidad.
c
Representen en sus carpetas los valores de la tabla en un sistema de ejes cartesianos.
lr*ffiffiffi,'
CONTENIDOS
19. Representen los siguientes puntos en un sistema de ejes cartesianos.
a = (2;6)
c:(5;18)
d:(7;74)
b = (6;0)
lE.l7.lE.lg
mmmm
e:(8;9)
f:(72;5)
20. Observen e[ gráfico y escdban las coorde-
22.
Resuelvan.
a. lndiquen cuál o cuáles de los siguientes
puntos están bien representados en eI sistema de ejes cartesianos.
a : (2;7) c: (7;7)
e : (7;3)
b:(5;6)
d:(7;2)
f:(8;6)
nadas de cada punto.
e
e
b
c
d
d
b
)
a
0
0
21. Ubiquen el vértice que htta para que se
b. Representen correctamente los puntos mal
forme [a figura indicada en cada caso.
ubicados.
a. Cuadrado.
23.
Lean atentamente
y respondan.
Una enfermera registró la temperatura de un
paciente en e[ siguiente cuadro.
d
a
0
b. Romboide.
a
c
a
Representen los valores de la tabla en los
ejes cartesianos.
b. ZLa relación es función? Expliquen [a respuesta.
c
ZSe pueden
unir los puntos del gráfico?
iPor qué?
2/l.
0
c
0
ZLas soluciones son únicas? Si no lo son,
indiquen otra posibilidad.
Escriban ejemplos según la condición.
a. Dos relaciones directamente proporcionales.
b. Dos relaciones inversamente proporcionales.
c
Dos relaciones no proporcionales.
Cuso:-
Feth¡:-/-
25.
28.
Resuelvan.
a Completen [a tabla para que sea una función de proporcionalidad directa. lndiquen la
constante de proporcionalidad.
b. Representen los datos en un gráfico cartesiano.
Resuelvan.
Héctor, el dueño de una estancia, se irá de vacaciones por 74 días y deja a Úrsula a cargo de
sus cinco caballos. Respetando la dieta indicada
por el veterinario, la cantidad de alimento que
le deja alcanza para esas dos semanas.
a. Si antes de irse, Héctor trae dos caballos
más, pero no agrega comida, ipara cuántos
días alcanzará?
b. Si solo hubiera dos caballos para alimentar
con la misma cantidad de comida, apara cuántos
días alcanzará e[ alimento?
26. tean atentamente y
c ila
resuelvan.
relación es una función de proporcionalidad directa o inversa?
d. Completen la siguiente tabla de acuerdo
con [a información anterior.
Para el cumpleaños de Julia, su mamá está
preparando un gran bizcochuelo y necesita tres
sobres de preparación.
cnsAffiq
3 cucharadas de leche tibia.
2 huevos.
5 cucharadas de agua.
200 g de manteca derretida.
a. ZQué cantidad de cada ingrediente necesita
la mamá de Julia?
b. Las variables Zse relacionan en forma directamente proporcional? Si es asÍ, indiquen cuál
es su constante.
e. Representen [a información de la tabla en
un sistema de ejes cartesianos.
29. lndiquen si las siguientes relaciones son
rectamente proporcion ales (DP), inversamente
proporcionales (lP) o no proporcionales (NP).
di
a
27.
Resuelvan.
Gabriel compró las entradas para él y sus cinco
amigos, para asistir a un recital.
e Si pagó $9oo por las seis entradas, Zcuánto dinero le tiene que dar cada
b. Completan la tabla.
La cantidad de harina y de pizzas que se
pueden hacer con
.,,u.f-]
b. La cantidad de agua para regar una planta
y su crecimi.nro.
amigo?
[-l
c- La cantidad de agua que arroja una manguera por minuto y el tiempo que tarda en
llenar una piscina.
d. La superficie representada de una provincia
en e[ mapa y tos kilómetros cuadradoi que
abarca dicha provincia dentro del territorio
c
ZCuál es [a constante de proporcionalidad?
ü
Representen la información en un gráfico.
nacional.
t-l
AuroEvAruActóru
30.
Observen el gáfico
y respondan.
Mariana realizó una excursión a las termas de Cacheuta. El siguiente gráfico representa la excursión
desde que partió del hotel hasta su regreso, en función del tiempo.
a. ZCuántas horas estuvo fuera del hotel?
b. iCuánto tiempo estuvo en las termas?
c. ¿A cuántos kilómetros del hotel se encontraban las termas de Cacheuta?
d. iRea lizaron alguna parada en el camino?
)
¿A
la ida o a la
vuelta?
e. ¿Cuántas horas duró el viaje de regreso?
31. Resuelvan.
Pablo tiene varias peceras con forma de prisma. Todas miden 40 cm de largo y 20 cm de ancho,
pero distintas alturas. La primera mide 60 cm de altura; la segunda 50 cm y la tercera, 70 cm.
a il-a altura de cada pecera y su volumen son variables directamente proporcionales? iPor qué?
)
b.
ZCUáI
c
Completen la siguiente tabla y luego representen la informacíón en un sistema de ejes cartesianos.
es la constante de proporcionalidad? ZCuál es la variable independiente? iY la dependiente?
I
I
32.
P¡ensen
y resuelvan.
En la reunión de consorcio del edificio de Ana, decidieron cambiar la decoración
delftente.
El costo de
I
la reforma es de $Z fOO y será dividido entre todos los propietarios.
I
a. Si en total son 14 los propietarios, Zcuánto dinero deberá abonar cada uno? iY si fueran 30 propietarios?
I
b. Las variables,
i
¿se relacionan en forma directa o inversamente proporc¡onal? lndiquen la consproporcionalidad.
tante de
I
I
L
t
c
Completen la tabla teniendo en cuenta la información de los ítems anteriores y representen
los puntos en un sistema de ejes cartesianos.
f,onrrnruns
Z!.
Ctasificación de los
cuerpos.
21. Potiedros regulares.
E!. Desarrollo plano
de
cuerpos.
EJ. Punto, recta y plano.
Sm¡eoór r¡rrcrrl DE APREIDIZAIE
1. Observen [a imagen y resuelvan.
a
El siguiente texto tiene datos incorrectos. Léanlo atentamente y escríbanlo como corresponde.
La gaseosa tiene forma de rectdngulo; el helado, de triángulo y la pelota, de círculo. Esta últi-
ma es una figura que rueda, por lo tanto su superficie no es plana.
b. iQué errores encontraron?
c La cajita de jugo, ies una figura o un cuerpo? ZQué forma tiene?
d. Comparen e[ texto que escribieron con el de sus compañeros.
nHErywwrymr
Clasificación de los cuerpos
Los cuerpos se clasifican en:
.
Poliedros: tienen todas sus caras planas.
Prisma: sus cans latentes son panlelogramos y sus bases son potígonos panletos.
.
PiÉmide: todas sus caras concurTen en un
vért¡ce, excepto una que es [a base.
Redondos: tienen a[ menos una cara no plana.
circunferencias
máximas
L
)
y expliquen las respuestas.
Un cubo, ies un prisma?
Respondan
a
b. ZQué figuras geométricas son las caras laterales de las pirámides?
c iQué cuerpos tienen una sola cara plana?
d. Las caras laterales de todos los poliedros, ison paralelogramos?
rt
I
t#il?ilJ.''."
los cuerpos
-)at
1. Unan con flechas, cuando sea posible.
o Prisma
r
Pirámide
o Cilindro
o Cono
o Esfera
2. gscriban los nombres de los cuerpos que forman los siguientes objetos.
a.
c.
e.
(
ffi
(
b.
d.
g ffi
(
HETWffiWWWi
Poliedros regulares
Se llaman poliedros regulares a aquellos en los que todas sus caras son polígonos regulares iguales.
Existen solo cinco poliedros regulares.
)
Tetraedro
Cubo
Sus caras son cua-
Sus caras son seis
Sus caras son
tro triángulos equi-
cuadrados iguales.
ocho triángulos
láteros iguales.
Octaedro
equiláteros iguales.
?Eb
gtrpg
tpt\ tog
TSUbS
\g5.ong,r.
'Un
eoi'lo\€CíA
Q¡l¡elbRqutAR
)
b&ugTaEr\
ToStl9
Dodecaedro
Sus caras son
doce pentágonos
regulares iguales.
)
En
cA$s\q[E$...
lcosaedro
Sus caras son
veinte triángulos
equiláteros iguales.
todo poliedro se verifica la relación de Euler.
(+\/=[+ I
C: cantidad de caras
V: cantidad de vértices
A: cantidad de aristas
)
1. Respondan y expliquen las respuestas.
a. Un prisma de base cuadrada, ies un poliedro regular?
b. iTodas las pirámides son poliedros regulares?
c. Las caras de una pirámide regular, Zpueden ser triángulos isósceles?
d. La relación de Euler, ise puede aplicar a los poliedros no regulares?
I tl
3.
i:1,'Jl*"3u,ares
Marquen con una
X los poliedros
*c
ur0
4.
regulares.
"D
".c
a.!
f.o
Unan con flechas cada cuerpo con el número de vértices que tiene.
a Cubo
b. Tetraedro
c
Octaedro
d. Dodecaedro
e. lcosaedro
I
c$
o2O
CI¡
¡15
(
o72
r$
5. Completen la tabla y verifiquen la relación de Euler.
Cubo
(
e
A
Tetraedro
I
A
@
@
(
SgEBgW
Desarrollo plano de cuerpos
El desanollo plano de un cuerpo es la forma del cuerpo cuando se lo desarma.
¡
I
El desarrollo de un cuerpo permite conocer las figuras que lo forman y también, construirlo. Para
ello, es necesario agregarle al desarrollo del cuerpo solapas en algunas de sus aristas para poder
doblarlas y pegarlas uniendo las caras.
I
1. Respondan y exptiquen las respuestas.
a. El desarrollo de un cubo, ipuede tener más de 6 cuadrados?
b. El desarrollo de una pirámide de base triangular, ipuede tener rectángulos?
c
E[ desarrotto det cono, Zes igual al de] cilindro, pero con solo un círculo de base?
F
F*
H
r tt
igyl3il3'0i","
de cuerpos
6. Completen la tabla.
7.
lndiquen el nombre del cuerpo al que peÉenece cada desanollo.
a.
8.
c.
e,
Marquen con una X el desanollo conespondiente al siguiente cuerpo.
'.o
..o
bc#
do
til
9.
ACTIVIDADES
Desarrollo plano de cuerpos
Marquen con une
X cl nombrc de los siguhntes cuerpos teniendo en cuenta su desanollo.
b.
)
f'-l
e,im,
de base
triangular.
f-.|
Prisma de base cuadrada.
fl
)
eirariae de base cuadrada.
10.
f-l
tr,r,n. de base triangular.
[-l tr'rr.
Prisma de base cuadrada.
ü
ü
ei,ariae de base cuadrada.
Respondan teniendo Gn cuenta quc
de base triangular.
Prisma de base cuadrada.
Pirámide de base cuadrada.
cl cutfpo está formado por cuboe i¡uelcs y se pintó de
viohta tod¡ la superllcie.
a. iCuántos cubos forman el cuerpo?
b. iHay algún cubo que tenga todas las caras pintadas?
)
c
iCuántos cubos tienen solo dos caras pintadas?
d. iHay cubos que tengan la mitad de sus caras pintadas? iCuántos?
e. iCuántos cubos más debefla tener el cuerpo para que queden cuatro cubos con solo dos caras
pintadas? ¿Dónde los ubicarían?
)
1L
)
Marquen con una
X los prism.s quc conesponden al siguiente
desanollo.
".o
"o
b.D
d.o
rtt
tffim*decuerpos
lil.
Completen con las caras que faltan para obtener el desanollo del cuerpo indicado. Luego,
copien los desanollos y armen los cuerpos.
¡.
c
Cilindro.
Prisma de base hexagonal.
d. Cubo.
b.Prisma recto de base triangular.
13, Conshuyan un octaedro regular y numeren sus cafas como se muestra en la imagen. Luego,
desarrollo que conesponde al cuerpo que armafon.
marguen con una
lel
w
".oA
.o
MENIEIGTnlA
La caja en la que Martín guarda sus ahorros tiene forma de prisma rectangular. Si decide
pintarla de modo que dos caras que tengan una arista en común no queden pintadas con
mismo color, icuántos colores diferentes necesita como mínimo?
e
l(
L*J L*J i-J,*J t*i
tJ t ilJ
Punto, recta y plano
En el siguiente prisma se pueden obser-
var los tres elementos fundamentales de la
geometrÍa del espacio: plano (u), recta (A)
y punto (b).
Cada cara del cubo representa una porción de un plano, las aristas son segmentos
)
de rectas y los vértices son los
puntos
donde concurren tres o más aristas.
En e[ siguiente cubo, las rectas A, B
y
D son coplanares porque están incluidas en un mismo plano.
Las rectas coplanares pueden ser secantes (tienen
un punto en común) o paralelas (no tienen puntos en
común).
DyCsonoecanles.
Ay ts eon Varalelas.
)
Las rectas secantes pueden ser perpendiculares (se
intersecan formando cuatro ángulos rectos) u oblicuas.
ts
y C eon perpendicularee.
Ay
)
D son oblicuas.
Si dos rectas no están incluidas en el mismo plano,
se denominan alabeadas.
D
y Eson alabeadae.
1. Respondan y expliquen las respuestas.
)
a. iCuántos puntos determinan una única recta?
b. iCuántas rectas pasan por un punto?
c. Dos rectas paralelas, ipueden tener puntos en común?
d. Dos recías alabeadas, Zson perpendiculares?
L
r tl
ffiil:'l?,:"p,ano
14. ttarquen con unaX las opciones
a. Por un punto pasan...
[-l
[-l
f-l
b.
conectas.
Dos rectas perpendiculares...
[-l
O
[-l
,non'r.s rectas.
un, sola recta.
,oto dos
c
rectas.
d.
Dos rectas paralelas...
,on secantes.
no tienen puntos en común.
torrun cuatro ángulos de
9oo.
Dos rectas alabeadas...
f-l
,on secantes.
C
[-l
no tienen puntos en común.
[J
no tienen puntos en común.
pu.o.n ser alabeadas.
f-l
ron perpendiculares.
15.
son paralelas.
Nombren dos rectas gue cumplan las condiciones indicadas en cada caso.
(
a.
Dos rectas perpendicutares.
b.
Dos rectas
paralerus.f-l
C tO
yO
yO
d. Dos rectas oblicu.r.O yO
e. Dos rectas alabeuaur.f-l vC
c
Dos rectas
secantes.[-l
I
I
I
¿¿-------
I
16. Pintcn con el cdor indicado.
a
Azub
dos planos paralelos.
b. Roio:
dos planos perpendiculares.
c Vcrde
dos plaños oblicuos.
I
(
lnrsEHAElún
17. filarquen una X donde conesponda.
ffi
t0.el.tt.t3
según conesponda.
a. Las pirámides tienen un solo vértice.
b. Todos los poliedros son prismas
c. El cono tiene un solo vértice.
El cuerpo está compuesto por:
[-l un cuuo.
C
c
)
o
Un prisma de base rectangular.
Una pirámide de base cuadrada.
Una pirámide de base triangular.
o F (rabo)
18. Completen con V (Verdadero)
[-')
C
[-l
d. La base del cono es una circunferenci".
O
e. Un prisma de base pentagonal tiene cinco
aristas.
[-l
19. Compteten teniendo en cuenta la relación
de Euler.
b.
a Un poliedro regular que tiene 6 caras,
ces y
Ouristas
8 véfti-
es un
tiene 12 caras,
vértices y 30 aristas.
E[ cuerpo está compuesto por:
Un cubo.
c. Un poliedro que tiene
[-l
caras, 6 vértices
y 12 aristas recibe el nombre de
Un prisma de base rectangular.
Una esfera.
Un cilindro.
d. Si un poliedro tiene 4
..r.r,
f-l
vértices y
6 aristas es un
Un cono.
20. Verinquen si se cumple la relación de Euler
en los siguientes cuerpos compuestos.
a.
El cuerpo está compuesto por:
)
C rr prisma de base triangular.
fl unu pirámide de base rectangular.
O ur prisma de base rectangular.
O rr cilindro.
[-l
un.
esrera.
b.
21. Marquen con una X el desanollo que
conesponde a un cubo.
'.o
b.o
23. Completen
con
ll
(paratelas) o
I
(perpendi-
culares). Pueden ayudarse realizando los gráficos.
a. A
ll
B; B llC, entonces O
C a.
b. A llB; B I C, entonces oO a.
c. A l- B; B ll C, entonces OO a.
d. A l- B; B I C, entonces OO a.
e. A llB; B l- C; D llC entonces OO
f. A -l- B; B I C; C l- D, entonces O O
(
o.
O.
24.
Dibujen en sus carpetas dos rectas que
cumplan con las condiciones indicadas en cada
caso.
a. Que dividan el plano en cuatro regiones.
b. Que dividan el plano en tres regiones.
c Que dividan el plano en dos regiones.
d. ZCómo son los pares de rectas trazados en
cada uno de los casos anteriores?
"o
25.
Realicen en sus carpetas un gráfico que
cumpla con las siguientes condiciones.
AllB;
d.o
(
26.
cI& D-tBvEllD
Copien en sus carpetas los siguientes cuer-
(
pos y pinten en cada uno de ellos un par de planos que cumplan con las condiciones indicadas.
a. ü y p son perpendiculares.
t
I
¡
-¿----t22.
Escriban rectas que cumplan con las condi-
ciones pedidas en cada caso.
b.eyDsonoblicuos.
c.
a. Tres rectas paralelas.
b. Un par de rectas paralelas.
c Un par de rectas perpendiculares.
d. Dos pares de rectas oblicuas.
TE
I
y y son paralelos.
(
AuroEvALUAclón
27.
Completen.
a.Unapirámidede6carastiene[lvérticesysubase",unE
h
Un pdsma de 8 caras
c
Un prisma de 10 vértices tiene
2&
Compteten la tabla.
29.
trtarquen con una
tiene[-l
afistas y su base es un
[-l
.urm y su base es
)
X
los desanollos que corresponden a este cuerpo.
*c
""o
)
u!-+ af$
!10. Marquen con una X la opción que representa las siguientes relaciones entre rectas.
AllB,All cyDLc
a.b.c.r
f,nnrsnrons
ill+. Sistema sexagesima[.
Operaciones.
35. Ángulos complementarios
y suplementarios.
3[. Ángutos adyacentes
y
opuestos por e[ vértice.
37. Mediatriz de un segmento
y bisectriz de un ángulo.
Srrutclót t¡uctAt
IrE ApRE¡rDrzAlE
1. Observen [a imagen y resuelvan.
a. iDónde rebotará la bola violeta si se le pega con la blanca en el centro? Dibujen [a trayectoria
que hace [a bola blanca hasta pegar en [a violeta y [a trayectoria de la violeta hasta tocar [a
banda.
b. iDónde ubicarÍan [a bola blanca para que haga entrar a [a violeta en un agujero? Dibujen las
trayectorias como en el punto anterior.
c Comparen e[ ángulo que forman las dos trayectorias de la bola violeta con el que forman las
trayectorias de la bola blanca.
d. Comparen las respuestas con sus compañeros.
Md
I
k#
SÍstema sexagesimat Operaciones
El sistema sexagesimal se utilíza para escribir medidas de ángulos. En este sistema, si se divide
un giro completo en 360 partes iguales; cada una de esas partes se denomina grado. para ángulos
menores que un grado se utilizan e[ minuto O y el segundo (').
10
.
: 60'
Un grado equivole o 60 minutos.
Adición de dos ángulos.
19'
* 48"
65o 35'
113" 54'
.
= 60"
107.
67" 41',
95"
35"
.
Multiplicación de un ánguto
por un número natural.
17" 51'z 5"
,¿
510 153', 15"
,o-azo' -+ 2 veces 6o'
/\=-/
530 33'
92'
,pú ¿y{
40"
st"
47"
51'
4"
al E g¡sÉrA Hlgsh,|At €oN Hur im*nÉ
lcÉ gflDcÉ. tR EüüPtDr Utl ffiltD FqnA^É A
6 lt¡rrJÉÉ... éqÉtE IÉCíg?
qE ei [Ag¡AlGtÉ, ffib6,ltoY €do
$É,
*
lJn minuto equivale a 60 segundos.
Sustracción de dos ángulos.
42"
52"
1'
113" 55',
7'
iñIffiA
n qgtgtcfñr€srúcA...
.
División de un ángulo
por un número natural.
86" 17' 12" | 2
86" 16')60" 43" B', 36"
1'/
- o"/-(-+72"
72"
15"
o')
1. Respondan y expliquen las respuestas.
a. iPor qué se llama sexagesimal aI sistema para la medición de ángulos?
b. zcuát es el procedimiento para encontrar el equivalente a l.5o en minutos?
c. ZCómo se pasan 72OOO" a grados?
d. La suma de dos ángulos, Zes correcto escribirla como 12o 65, 7g"?
Cuno:-
Fecha:-/_
It
t+ tfl'*:T.t.:ses¡mat. operaciones
1.
Expresen en segundos.
=f-l
a.23'
b.20:
2.
:
t-l
d. 3' 4o'= t-l
c
1Oo
3'
Expresen en minutos.
a. 360":
b.
450
.-3o2'=D
d. 15o : f-l
f-l
!20"
=
Unan con flechas las operaciones que dan el mismo resultado.
e 32o 25'
a. 43o 75' + 27o 35' =
3.
:
b. 79" 20' c.732o 40' ;3 =
d. 1304o 10' : 8 =
740 30',
4.
Escriban el cálculo
77o
.
.
78o 30" + 85o 45"
3' 20"
87o 20'10"
-
=
43"
:
6'50" =
y resuelvan.
a. El doble de [a suma entre
b.
.2:
.4
o
15o 35'
y 36" 42'.
La diferencia entre la tercera parte de 7260 45"
y 32o 7'.
l
c
La suma entre [a mitad de 47"
d.
El cuádruple de 650 23'menos 23o 45".
5.
34'y el doble de
l
26o 56"
Completen para que se verifique la igualdad.
". D
b. 1650 40'30'
=
*D
=
+ 35o 5o'
c.
27o
ro"
o.
73o 5'
f-l]
t.D
t[-l
".
779o 77'
6. Completen.
tn.oo
*O
a.
¡o'
rs"
7200 57'
5"
b. 840 40'
oo"fl
O
30"
o
37'
2e"
c.
35o
O.2
30"
C3r'O
d.
7730
C
*.0'
t*
o'l
O ,u'
z
4
:
43o
10' 30'
= 26307'75"
.4:r6eo22'
(
iri
I
jl
it." JÍ ;i,.il
,i¡t,:1rr
il",¡l- ji
Ángutos comptementar¡os y suplementarios
WW
Para nombrar un ángulo, pueden utilizar una de las siguientes formas:
aob, se escribe el vértice en e[ medio;
6, se escribe solo el vértice;
0, se escribe una letra griega.
Los ángulos se clasifican según su amplitud en: nulos (miden 0o), agudos (miden más de Oo y menos
de 90o), rectos (miden 90o), obtusos (miden más de 90o y menos de 18Oo) y ltanos (miden lgOo).
.
Dos ángulos son consecutivos cuando tienen
el vértice y un lado en común.
Dos ángulos son complementarios
Dos ángulos son suplementarios
cuando suman 90o.
cuando suman 1800.
--¿k_
i
y d son complementarios
i
d
es et complemento de d.
es et complemento de f.
5i
Q mide75', enfoncee &. mide 15',
porquef+&=90'.
?orque 90"
)
- 75' = 15'.
Py6solsuplementarios
RorqueB+6:1800.
B es el suplemento de 6.
n'n
6 es el suplemento de $.
5i ^/\
B mide75',entonces 6 mide 1O5',
?orque 1BO' - 75' = 1O5'.
1. Respondan y expliquen las respuestas.
a. Si dos ángulos suman 9Oo 7', rson complementarios?
b. Si A y B son suplementarios, ise puede asegurar que d
:
c. aSe puede calcular el complemento de un ángulo obtuso?
d. ZCuánto mide el suplemento de un ángulo recto?
B?
I tS
iflL1l?^S"Tprementarios y suprementarios
7. Coloquen
(
) o =, según
[-l
b. Suplemento de 1560. (-l
a. Suplemento de 1300.
c
Complemento de
4t".
C
d. Suplemento de 166o 56'.
corresponda.
Corptemento de
10.
Supt.rento de 745.. 30'.
Suplemento de 135o.
O
Complemento de 78o 45".
8, Marquen con una X los ángulos consecutivos.
".o
JP
b.o
L
d.o
\
9.
Ptanteen las ecuaciones, resuelvan e indiquen el valor de cada ánguto.
c. Datos:
a. Datos:
0=3x+10o
0=2x+35o
d y fi .on complementarios.
á:4x-1oo
a:( 10=D
e=f-]
b. Datos:
d. Datos:
6:5x+1000
0 y 6 son suplementarios.
t=+^
ff:zx-too
ft,=3x+96"
á:8x-4Oo
fi=D6:D
6:
?=
[-]
,^ =
V
v
[-l
10. Planteen las ecuaciones y resuelvan.
a
El complemento de un ángulo, dismínuido en 30o, da por resultado 21.o. iCuánto mide el ángulo?
b. La suma entre el complemento de un ángulo y el suplemento es igual a su doble. ZCuánto
mide el ángulo?
NHHHHMHHI
Angutw adyacentes y opustos por et vértÍce
-
&rguhÉ a{¡acents
Dos ángulos son edyacentcs cuando son consecutivos y suplementarios.
d*fi=139o
Angubs opuestos por et rÉrtice
Dos ángulos son opucstos por el vértice cuando tienen el vértice en común
semirrectas opuestas.
y sus lados son
0 y $ ton opuestos por el vértice.
ft y f son opuestos por el vértice.
Los ángulos opuestos por el vértice son iguales.
F
li
."
[ñl*a=1800
:
liJ. a 180.
&nseristus
\-
itr'flcffi!-'
ECIIIú',E
gHf qrÉ
-rmsr
tsr¡AB
'mflti-
Respmden y expliquen las respucstas.
e Si dos ángulos tienen un lado en común, ison adyacentes?
b. iTodos los ángulos adyacentes son suplementarios?
Los ángulos opuestos por el vértice, isiempre son suplementarios?
d, iTodos los ángulos suplementarios son adyacentes?
e. Si dos ángulos miden lo mismo, ase puede asegurar que son opuestos por el vértice?
c
rtE
ACÍIVIDADES
Ángutos adyacentes y opuestos por e[ vértice
11. Completen la tabla teniendo en cuenta el gráfico.
(
12. Escdban las ecuaciones, resuelvan y calculen el valor de los ángulos dados.
Datos:
d, = 2x - 18o
c
a.
2oo
/
0=[-l
ft=[-l
b. Datos:
d. Datos:
6:3x+33o
6=8x-47o
6:3x-13"
f:f-+75o).4
6=fl
\
t,=2.(zx+5o)
^:77x-
,
'=s*-t;
a=f-l
Datos:
a=D
?
:
f-]
,/
)K
a=D
6=f:_l
13. Tncen un par de ángulos que cumplan con las condiciones indicadas en cada caso.
b. Que tengan el vértice en común
a. Que tengan un lado en común
y no sean opuestos por el vértice.
y no sean adyacentes.
(
(
HHHWHMHMI
Hiaüiz
de un segmento y bisectriz de un ángulo
nediúiz de un segmerrb
La mediatslz de un segmento (Mz) es la recta perpendicular gue pasa por su punto medio. Los
puntos de la mediatriz equidistan, es decir, están a la misma distancia de los extremos delsegmento.
Para trazar la mediatriz pueden seguir estos pasos:
1. Se apoya el compás en uno de los extremos del
punto medio
detAE
segmento con una abertura mayor a la mitad del
segmento y se traza una circunferencia.
2. Se repite el procedimiento apoyando en el otro
extremo del segmento, con la misma abertura.
3. Se dibuja la recta que determinan los dos puntos
de intersección de las circunferencias.
¡liseüiz de un ángulo
La bisectriz de un ángulo (Bz) es la semirrecta que lo divide en dos ángulos iguales. Los puntos
de la bisectriz equidistan de los lados del ángulo.
Para trazar la bisectriz, pueden seguir estos pasos:
1. Se clava el compás en el vértice o
y se traza
un arco que corte a los dos lados del ángulo.
2. Con la misma abertura se apoya en o y se traza
un arco; luego, se apoya en b y se traza otro
arco que corte el anterior, por ejemplo, en p.
3. Se dibuia la semirrecta oÉ, qu. es la bisectriz
del ángulo.
L
)
Respondan y expliquen las respuestas.
a. iCualquier recta perpendicular a un segmento es su mediatriz?
b. La bisectriz de un ángulo, ilo divide en dos ángulos consecutivos?
c
iSe puede trazar la mediatriz de una recta?
d. aSe puede dividir un ángulo en cuatro ángulos iguales utilizando la bisectriz?
e. iSe puede trazar la bisectriz de un segmento?
ru7
ACÍIVIDADES
Mediatriz de un segmento
y bisectriz de un ángulo
LLL
14. Tracen la bisectriz de cada uno de los siguientcs ángulos.
a'
f
"1
L
15. Tracen la mediatriz de cada uno de los siguicntes segmentos.
a.
b.
(
16.
Resuelvan.
a. Tracen la mediatriz del ab. Llamen o
al punto medio del á5'.
b. Marquen el punto c sobre [a mediatiz.
c Tracen la oñ, bisectriz del c6b.
d. Tracen la oi, bisectriz del m6b.
e. Completen con las medidas de los ángulos
I
obtenidos.
a6c:t-l m6a:f-l
'6t
=f-l
.6,
=D
17. Completen el rt teniendo en cuenta las indicaciones en cada caso.
b. La recta M es la mediatriz del segmento que
a. La recta R es mediatriz del rt.
representa la mitad del ñ.
F
menteACflVA
de
fn",:J,:'.T :;:H;-gmento
I
(
7'5 cm en cuatro sesmentos iguales usando solo er
compás
(
I
coilTEHTDOS
TEEHAEIEN
18. Resuelvan.
a. Tracen un par de ángulos opuestos por el
vértice y un par de ángulos adyacentes.
b. Tracen las bisectrices de cada uno de los
ángulos del ítem anterior.
c. Completen las siguientes oraciones teniendo en cuenta los gráficos realizados.
r
Las bisectrices de los ángulos opuestos por
#i'e5-tE.t7
20.
Elijan un par de los siguientes ángulos de
modo que cumplan con la condición indicada
en cada caso.
0=
28o 30'
F = 77" 30'
151o 30'
0 = 18o 30'
a. La suma es un ángulo obtuso.
b. Son ángulos suplementarios.
c. Son ángulos complementarios.
6:
el vértice forman un ángulo
21. Tracen un par de ángulos que cumplan
¡
las condiciones indicadas en cada caso.
a. Un par de ángulos complementarios no
Las bisectrices de los ángulos adyacentes es-
con
tán incluidas en rectas
consecutivos.
o Las bisectrices de los ángulos adyacentes
b. Un par de ángulos suplementarios no consecutivos.
forman un ángulo
19. Calculen los ángulos indicados.
a. Datos:
oñ
bisectriz.
c. Un par de ángulos opuestos por el vértice
y complementarios.
d. Un par de ángulos adyacentes e iguales.
e. Un par de ángulos opuestos por e[ vértice
y suplementarios.
22.
Escriban la medida de cada uno de los
ángulos indicados.
a. El suplemento de 73Oo 25' - !2o 50'.
b. El complemento de 35o 30" .2.
c Elángulo adyacente al que mide 72o +75o 75'.
d. Cada uno de los ángulos que se obtienen al
trazar la bisectriz del ángulo que mide 733o 40'.
e. El ángulo opuesto por el vértice al que
mide 145o 20' - 37o 5O'.
t-r
v:
r-l
B=
cf,=
b. Datos:
23. ¡n cada caso, tracen el ángulo a6b
do que oñ es bisectriz del mismo.
RI5
b.
t-l
6: t-l
lt:
Q=
g=
t-l
f'-l
Curso:-
Fecha:-/-
sabien-
I
24. Planteen la ecuación e indiquen los valores
de cada ángulo.
a Datos:
25. Marquen una X donde conesponda teniendo en cuenta el siguiente gráfico.
Datos:
é:3x-3o
RJ-S
F:5x+2o
oñ
es bisectriz del &.
ñi bisectriz.
b. Datos:
6=6x
ft,=2x+50"
T mediatriz del á6'.
c
Datos:
á=4x-1Oo
F=5x+28o
26.
Resuelvan.
Datos:
6"22=77o
m6t = 45o
oi bisectr¡z de 0.
oñ bisectriz de &.
d. Datos:
ft,=3x-76o
6:
oñ
5x + 40o
bisectriz
cr,
c&*fi
b.p
d.0:z
a
l-
".fi*á,
f.0-a
AuroEvAruAcrótr
27. escriban el cálculo y resuelvan.
a
b. La mitad de la diferencia entre el
El doble del complemento de 34o 25'
suplemento de 12o 70'
más la tercera parte de 158o.
y
560 34'.
28. Completen con'a veces', *siempre" o "nunca', según corresponda.
a Si dos
ángulos son suplementarios, entonces son iguales.
b. Si dos ángulos son adyacentes, entonces son obtusos.
c
El complemento de un ángulo de 120o es el ángulo de 60o.
d. Si dos ángulos son suplementarios, entonces son rectos.
e. Dos ángulos adyacentes son suplementarios.
29. Planteen la ecuación e indiquen la medida de los ángulos indicados.
Datos:
fr bisectriz
d=3x-10o
9:x*4oo
o
p: o
x:
30. Tncen la mediatriz conespondiente al 16 y
h
c
bisectriz del
t.
ct:
6=
o
o
r
r
J
f,onrenlnns
Triángulos. Elementos y
propiedades.
Construcción de triángulos.
Cuadriláteros. Elementos y
propiedades.
Construcción de
cuad riláteros.
Círculo y circunferencia.
Elementos y propiedades.
Construcción de
circunferencias.
Potígonos.
Construcción de polígonos
regulares.
f
II
f
J
t-
l
I
--:' tl
k 54
&
4:
I!4
Strunclór¡ tiltctAl DE ApRENDtzAIE
1. Observen la imagen y resuelvan.
a- ZEn qué objetos se pueden identificar figuras de tres tados? Zy de cuatro lados?
b' ZHay algún objeto en el que se pueda identificar una figura que tenga todos sus lados
iguales?
c' Modifiquen las preguntas anteriores para que las respuestas sean únicas. Luego, respóndanlas.
d. Comparen con sus compañeros las preguntas que realizaron.
k# j rr# t Hl
Triángulos. Etementos y prop¡edades
-
Los triángulos se clasifican según sus lados en:
Los triángulos se clasifican según sus ángulos en:
. Escalenos: todos sus lados miden distinto.
. lsósceles: tienen a[ menos dos lados iguales.
. Equiláteros: todos sus lados son iguales.
. Acutángulos: tienen tres ángulos agudos.
. Rectángulos: tienen un ángulo recto.
. Obtusángulos: tienen un ángulo obtuso.
|[ reOEqEüIiÁI
En todo triángulo se cumplen las siguientes propiedades:
E¡üt$' ef,aNoub
blbq)EmtE$lo
h-c es
la altura.
E¡ HM{frCA-.
VA6AiTETR
ullGnüuR
ivsnaams,
.
ESIIEb o
La medida de cada lado es menor que la suma de los otros dos.
áb-<ñ*ca
bc<ca+ab
ca<áT*61
.
La suma de los ángulos i4teriores es igual a 180o.
.
La suma de los ángulos exteriores es igual a 360o.
R¡rt'Eb...?
á*t*t:reo"
t*0*&:¡eo"
.
.
Cada ángulo exterior es suplementario con el ángulo interíor correspondiente.
AA
a+c,=1800 ii*fi =139"
t*f=139'
Todo ángulo exter¡or es igual a la suma de los dos interiores no advacentes.
e=d;t-- 0:a-t
f=á*t'
Dos triángulos son iguales cuando al superponerlos coinciden en todos sus puntos.
1. Respondan y expliquen las respuestas.
a. Un triángulo obtusángulo, ipuede tener un ángulo menor que 90o?
b. iSe puede construir un triángulo cuyos ángulos interiores midan 35o, 27o y
c
Un ángulo exterior, Zpuede medir más de 1800?
d. ZEs posible construir un triángulo equilátero rectángulo?
7780?
I tE
+ffiffi5,.*.ntos y propiedades
L Calculen las medidas de los lados y de los ángulos que faltan.
a El abc es isósceles y rectángulo.
b. El def es obtusángulo e isósceles.
2
Calculen la medida de los ángulos teniendo en cuenta las propiedades.
Datos:
Datos:
c
¡.
á=7x+3"
b=95"-2x
t,:4x+37o
L.
Datos:
6=77"
d = 4x- 8o
f = 6x- 350
*=t"-39'-'\-¡{\
9:7x- 47o
0=26o+3x
ü Datng; ---d=90'
j:2x+7"
k:80+3x
MHH MHMHHI
Construcclén de trlángulos
Conctrucclón de un Húngruto dados sus ücs lados
Datos: á5 = 4,5 cm; áE 3 cm; b-c = 4 cm
:
L
Se traza et ab. Se apoya la punta
ompás en a y con una abertura
at ag se traza un
arco.
del
igual
L
Se apoya [a punta del compás en
b
y con una abertura iguat at bc se traza
un arco que corte al anterior en c.
Con¡trucclón dc un ülúngulo d¡dos doe l¡dc y et
Datos: á6 = 3,5 cm; ac = 2,5 cm; á = 97"
áqulo compnndldo enüe elbs
ab
a
L
5e traza el á y con centro en a se
traza un arco con radio igual a[ á5 que
interseque a uno de sus lados en ó.
L
Con una abertura igual al ag se
apoya [a punta del compás en a y se
traza un arco que interseque a[ otro
tado det ángulo en c.
Cor¡¡ür¡cdón dc un trlún¡ub dqdoc dc úngiub y
Datos: á5 = 3,5 cm; f; = 65";'i = 42o
AD
a
A
l.
centro en a y radio iguat at
gan los lados de ambos ángulos.
a-b
que
interseque a uno de sus lados en D.
L
e[ b
6i
para formar
tt hdo somún t dbc
I 5e traza et á. se traza un arco con
Sobre D se traza
3. Se traza e[ segmento
el triánguto.
y se prolon-
3.
l¡
intersección de tas prolongacio-
nes de los tados de los ángulos deter-
mina e[ punto c det triánguto.
Respondan y expliquen las respuestas.
a iCuántos áatos se necesitan conocer como mínimo para construir un triángulo?
h Si se conocen las medidas de los tres lados, ¿cuántos triángulos distintos se pueden construir?
c iEs posible construir un triángulo conociendo la medida de los tres ángulos?
rt5
ACÍIVIDADES
Construcción de triángutos
3. Escriban Y (Verdadero) o F (rabo). Expliquen las respuestas.
a Se puede construir un triángulo cuyos lados miden 5 cm, 9 cm y el ángulo comprendido entre
ellos, de OO'.
O
ü. No se puede construir un triángulo cuyos lados midan 15 cm, 8 cm y
c
f-.)
9O'.
n
un triángulo con un ángulo exterior de 1030 y cuyos ángulos interiores no
adyacentes a él midan 50"
i.
cm.
No se puede construir un triánguto cuyos ángulos interiores midan 77o,24" y
ü Se puede construir
'q
O
y 53".
f-l
No se puede construir un triángulo cuyos lados midan 8 cm, 6 cm y r2 cm.
f--l
Resuelvan.
e. Completen la tabla con un gráfico de análisis de un triángulo que cumpla con las condiciones.
Propongan las medidas de los lados y los ángulos.
L iSe pueden construir
todos los triángulos? iPor qué?
XT
ACTIVIDADES
Construcción de triángulos
5, Respondan y expliquen cómo lo pensaron. Luego, conshuyan los biángulos.
iEs posible construir los siguientes triángulos utilízando solo el compás y una regla no graduada?
a. Un triángulo equilátero.
c Un triángulo escaleno.
b. Un triángulo isósceles.
d. Un triángulo obtusángulo.
6. Construyan los siguientes triángulos usando solo transportador y regla.
r. Un triángulo isósceles def cuya base mida 5 cm y los ángulos adyacentes a la base midan
b. Un triángulo obtusángulo mño de lados
ñn = 5 cm y no :7
cm, y ángulo
fr =
105o.
50o.
rtt
7.
ACT¡UDADES
Construcción de triángulos
Conshuyan los siguientes triángulos.
abc; ab.:3 cm; bc = 5 cm; ac = 6 cm.
a
¡. ¿ár; G
= 5,5 cm; á = 6o'; á =
55o.
c. gñi; Eñ'= + .r; Ei
: 5,5 cm; 0 = 105o.
^A:A
d. ikl; jk = 4 cm; jl
6 cm;
:
k = 40o.
menteACtrfilA
Diego está realizando una tarea para la escuela. Debe dibujar un avión, pero está preocupado
por el diseño de las alas. Sabe que deben tener forma triangular y que uno de sus ángulos debe
medir 60o. ZQué tipo de triángulo puede usar para dibujar las alas?
I
mHHmmHPHl
<
Cuadrilátelos. Elemenüos y propiedades
Un cuadrilátero es una figura que tiene cuatro lados, cuatro ángulos y cumple con las siguientes
propiedades:
,
No tienen lados
paraletos.
El romboide tiene
dos pares de lados La principal es
mediatriz de la
consecutivos
Tienen un solo par
de lados opuestos
paralelos.
En el trapecio
isósceles los lados
no paralelos son
otra.
iguales.
No se cortan en el
Los ángulos no
opuestos ni adyacentes a las bases
son suplementarios.
punto medio.
En el hapecio
lsésceles son
iguales.
iguales.
Tiene cuatro lados
iguales. Los lados
opuestos son
Tiene un par de
ángulos opuestos
En el hapedo lsósceles los ángulos
adyacentes a las
bases son iguales.
Son perpendiculares
y se cortan en su
punto medio.
Se cortan
Los ángulos
opuestos son
iguales.
mutuamente en su
Tienen dos pares
de lados paralelos
y opuestos iguales. Son iguales y se
cortan en su punto
medio.
Tiene los cuatro
lados iguales y
paralelos dos a dos.
Son iguales,
perpendiculares y
se cortan en su
Tienen cuatro
ángulos rectos.
nto medio.
La suma de los ángulos intedores de un cuadrilátero es igual a 3600.
L
Respondan y expliguen las respuesbs.
a
iPor qué el rombo, el paralelogramo, el rectángulo y el cuadrado son paralelogramos?
b. ¿Se puede decir que el cuadrado es un rombo?
c. iPor qué los trapecios no son paralelogramos?
f 3n
HXit-t-t::"
Eremenros
y pr*predades
8. Observen los cuadriláteros y resuelvan.
a. Completen la tabla teniendo en cuenta que puede ir más de un cuadrilátero por cada casilla y
que cada cuadrilátero puede ir en más de una casilla.
FIGURA A
ta
/\
FIGURA B
,-.,,.,----+f-
\/
\,r'
L-l n
FIGURA C
FIGURA
FIGURA D
FIGURA F
E
F;I
l_,_J
FIGURA G
FIGURA
I
FIGURA
J
*r;l
n
FIGURA H
b. iPudieron ubicar todos los cuadriláteros? ZQuedó alguna celda vacía? iPor qué?
9. Nallen la medida de los lados y los ángulos de los siguientes cuaddláteros. Expliquen la respuesta.
a. Trapecio isósceles.
b. Romboíde.
Mk M #EHEHI
Construcción de cuadriláteros
Para construir un paralelogramo, teniendo como datos los lados, pueden seguir estos pasos.
fi:4,5cm;acl=3cm
a
1. Se trazan dos rectas paratelas y
se determina sobre una de eltas
el
tado áb.
2. Con centro en a y abertura iguat at
áii,se traza un arco que corte a [a recta
paralela en d.
3- Con [a misma abertura y centro en ó,
se repite e[ procedimiento anterior
para obtener e[ punto c. Se trazan los
para determinar e[
segmentos áii y
paratelogramo.
[[
Para consEuir un rombo conociendo la medida de sus dos diagonales, pueden seguir estos pasos.
ac:6cm;bd:3cm
1. 5e traza una semirrecta, sobre etla
se determina la diagonal ái y se traza
la
mediatriz.l
2. Con centro en et punto medio de [a
diagonal se trazan dos arcos cuyo radio
sea [a mitad de bii y se determinan los
puntos b y d.
J. Se trazan los segmentos para formar
e[ rombo.
En ta página 95
pueden repasar
[os pasos para
trazar [a mediatriz
de un
1. Respondan y expliquen las respuestas.
a trs posible construir un único rectángulo conocíendo la medida de uno de sus lados?
b. iEs posible construir un rombo conociendo [a medida de sus diagonales? iEs único?
c ZEs posible construir un cuadrilátero conociendo dos de sus lados y el ángulo comprendido entre ellos? iEs único?
r3l
ACÍIVIDADES
Construcción de cuadriláteros
10. Construyan los siguientes cuadriláteros en sus carpetas, tracen las diagonales y respondan.
'
.
Cuadrado de 3 cm de lado.
Paralelogramo cuyos lados midan 3 cm y 4 cm.
.
.
Rombo de 3 cm de lado.
Rectángulo de 4 cm por 3 cm.
a. iCómo se clasifican los cuadriláteros que construyeron? iCuántas diagonales tienen?
b. En cada cuadrilátero, ilas diagonales miden siempre lo mismo? iSe cortan en su punto medio?
c iEn qué
paralelogramos las diagonales forman un ángulo recto?
11. Construyan los siguientes trapecios en sus carpetas, tracen sus diagonales y respondan.
. Trapecio rectángulo cuyas bases miden 5 cm y 3 cm y el lado perpendicular a las bases mide 2 cm.
. Trapecio isósceles cuyas bases miden 5 cm y 3 cm y su altura sea de 2 cm.
. Trapecio escaleno cuyas bases miden 5 cm y 3 cm'
a. iCuántas diagonales tienen los trapecios?
b. iCómo son las diagonales? ZSe cortan en su punto medio?
12. Completen teniendo en cuenta las actividades anteriores.
a. Los
tienen dos diagonales.
b. Las diagonales de los paralelogramos se cortan en su punto medio y tienen igual medida
yenel
en
y diferente en el
yenel
c. Las diagonales de los trapecios
no se cortan en su punto medio y tie-
nen igual medida.
d. Las diagonales de los trapecios
en su punto medio y tienen diferente medida.
no se cortan
lr
ASNUDADES
Construcción de cuadriláteros
13. Construyan los siguientes cuaddláteros usando regla y compás. Expliquen los pasos que realizaron para construirlos.
a. Un cuadrado cuya diagonal es el pr.
c Un romboide defg.
)
Pl-{r
)
b. Un trapecio rectángulo de altura
base menor sea igual a su altura.
ñ6,
cuya
d. Un trapecio isósceles abcd.
)
14. Resuelvan.
MartÍn desea cubrir un rectángulo de telgopor con cuadriláteros de diversas formas, de modo tal
que no quede espacio libre entre ellos.
a. ZPodrá usar solo rombos y trapecios?.Realicen un diagrama.
)
b. Si decidiera usar paralelogramos, icon qué otros cuadriláteros los podria combinar para que no
queden espacios libres? Realicen un diagrama.
)
rII
tSXIH'ff
de cuadriráreros
15. Calculen tos ángulos interiores de cada uno de los siguientes cuadriláteros.
c Datos:
a. Datos:
Paralelogramo efgh
0=
11Oo
b. Datos:
Romboide mnop
6=78o
P=¿n
A^A
Trapecio isósceles abcd
A:zá
d. Datos:
Rombo ijkl
ft:
og"
MENTEACTIVA
lulián y su papá quieren hacer un barrilete con forma de rombo; para ello tienen un papel rec'
tangular cuyos lados miden 60 cm y 90 cm. iCómo debe ser el barrilete para que sobre [a menor
cantidad posible de papet?
pueden construir en sus carpetas un rectángulo de 6 cm por 9 cm para analizar los posibles casos.
I
lnrEEHAmnn
16. Resuelvan.
a. iCon cuáles de los siguientes segmentos se
puede construir et a6c? Constrúyanlo.
. á5: 72 cm;6c = O cm; ca- = 6 cm
. á6 = 9 cm; b-c = 4 cm; ca- : 3,5 cm
. á6: 7,5 cmt b-c = 5,5 cm; ca- = 4 cm
A,
b. Clasifiquen e[ abc que construyeron según
sus lados y sus ángulos.
tE-tg-ln.3l
21. lean atentamente, observen lo que hicieron
los chicos y respondan.
La profesora les pidió a Laura, a Mariano y a
Georgina que resuelvan el siguiente problema:
"Colculen la medida de los dngulos exteriores
A
de un triángulo aQc cuyos dngulos interiores
miden:
á
:
65";'i
:
ss" y
t
=
80"."
17. Resuelvan y expliquen cómo lo pensaron.
a Con varillas de madera de 3 cm, 4 cm, 5 cm,
6 cm y 7 cm; icuántos triángulos diferentes se
pueden armar?
b. Con varillas de 3 cm,
4
cm, 6 cm y 9 cm;
Zcuántos triángulos diferentes se pueden
armar?
@
18. Construyan los triángulos cuando sea posible y clasiñquenlos.
a. G = 2 cm ;-ef = ¡ cm; ftl = 4 cm
b. gñ = 3 cm; ñJ = 2,5 cm;iE = 3 cm
C mn : 8 cm; nO = 4,5 cm; Om = 4,5 Cm
d.xy=2cm yz=5cm;zx=3
19. Resuelvan.
Paula necesita recortar doce triángulos rectán-
gulos cuyos lados midan 3 cm, 4 cm y 5 cm.
a. Si tiene una hoja de cartulina de 10 cm por
30 cm, Zpodrá recortar los triángulos que
necesita? ile sobra cartulina?
b. Si le sobra, icuántos triángulos más podria
recortar?
20.
Laura
a
&=180o-35o-80o:65o
0=180o-65o-80o=35o
,\
s
6=
@
180o
l
J -,,,.
I
65"
- 35o = 80o
Mariano
&=80o+35o=115o
6=65o+8oo=145o
A=65o+35o=1ooo
o
@
6,l
-
\,,
@i
o
eJ e
io
jo
i
in
Georgina
= 1800 - 650 = 1150
= 1800 - 35o = 1450
róu" - 80o = lOOo
= 1800
10oo
f
Resuelvan.
a. Construyan en una hoja cinco triángulos
isósceles cuya base mida 3 cm y los lados
iguales midan 4 cm.
b. Recorten los triángulos y armen un paralelogramo, un rectángulo, un cuadrado, un trapecio isósceles y un trapezoide.
c iPudieron armar todas las figuras? iPor
qué? ZCuánto miden los lados y los ángulos
de cada uno de los cuadriláteros que armaron? ZCómo calcularon las medidas?
a
iQuiénes resolvieron correctamente el pro-
blema?
b. iQué propiedades usaron?
iQué propiedad pueden usar para verificar
si las medidas que calcularon son correctas?
c
22. Piensen y respondan.
a
iTodo cuadrado es rombo? iTodo cuadrado
es rectángulo? iPor qué?
b. iTodo paralelogramo es rectángulo?
23. tlatten la medida de los ángulos
indicados.
24.
Construyan las siguientes figuras
y
respon-
dan.
a. Datos:
.A
abcd cuadrado; abe equilátero
a. Un triángulo rectángulo en el que los lados
que forman el ángulo recto midan 4 cm y 5 cm.
b. Un triángulo isósceles, cuyo ángulo desigual
mida 35o y sus lados midan 3 cm y 5 cm.
c. Un cuadrado cuyo lado mida 3,5 cm.
d. Un rombo que tenga un ángulo de 50o y
e
:
[-]
0:t-l
b. Datos:
fghi trapecio rectángulo
una de sus diagonales mida 3 cm.
e. Un trapecio isóscetes, cuyas bases midan
3 cm y 6 cm y dos de sus ángulos midan 60o.
f. Un paraletogramo que tenga un lado de
7 cm y los ángulos adyacentes a él midan 50o
y
0=x-¡2"
130o.
g. Un rectángulo cuyas diagonales midan
8 cm y formen entre sí un ángulo de 45o.
h. Las figuras que construyeron, ¿son únicas?
h:3x-72"
ZPor qué?
0:rl
c
A
:
t-]
25. Calculen los lados y los ángulos interiores
de los siguientes cuadriláteros, sin medir.
a. abcd paralelogramo
6cm
Datos:
^. rectángulo
iklm paralelogrTo; ikn
jn bisectriz del j
h:
D2.
\
k
0:t---l
p=
//'
-
d. Datos:
opqr rombo
'n\
.//
f
?=80'
26.
Calculen e[ valor de x.
abcd trapezoide
ft:[-l
z,z.'
6=
[-]
MM EgEEry$
Círculo
y circunferencia. Elementos y propiedades
Se denomina lugar geométrico a[ conjunto de puntos que cumplen con una condición.
Una circunferencia es
el lugar geométrico de todos los puntos del plano que se encuentran
a
igual distancia de otro ltamado centro.
Los siguientes son los elementos de ]a circunferencia.
E[ radio es [a distancia de cualquier punto de la circunferencia aI centro.
Una cuerda es un segmento que une dos puntos de una
circunferencia.
La cuerda de mayor longitud es la que pasa por el cen-
tro. Se llama diámetro y equivale a dos radios.
Un arco es [a parte de [a circunferencia determinada por
fic
dos puntos de [a misma. Por ejempto
es un arco de la
circunferencia (e[ punto del medio se utiliza para identificar
de qué lado de la circunferencia está e[ arco).
Se denomina ángulo central al que tiene como vértice el
centro de [a circunferencia.
ci es un ánqulo centra|
La circunferencia y todos los puntos del plano interio-
res a ella determinan e[ círculo.
circunfercncia
Posiciones relaüvas de dos circunfurencias"
Dos circunferencios son tongentes,
Dos circunferencios son secaatcs,
si tienen un único punto en común.
si tienen dos puntos en común.
1. Respondan y expliquen las respuestas.
a. El radio, ies una cuerda?
b. ZEI diámetro es la cuerda más larga?
c La circunferencia, iforma parte del círculo?
Dos cirxunferencias son a ncénttsi tienen el centro en común.
cos,
I I t
27.
tflillti?,tirrr-,encia.
Realicen los pasos
y propiedades
y respondan.
ElementoE: hoja,Iápiz, gancho maripoaa
?asos:
1. Marquen un
Etrenner¡ros
;
e hilo.
G"
punto en el centro de la hoja.
ra
2. Aten un extremo del hilo al gancho maríposa y claven el gancho en el punto que marcaron.
3. Aten elotro extremo delhilo allápiz.
G.
f-d'
4. Extiendan el hilo y tracen la figura que se forma.
a
a. ZQUé figura geométrica se formó? iQué representa el gancho mariposa en la figura?
iy el hito?
b. Si se mantiene e[ centro, pero se modifica e[ largo del hilo, icómo es la circunferencia que
se
obtiene?
c. Si se mantiene e[ largo del hilo, pero se modifica el centro, Zcómo es la circunferencia que
se
obtiene?
d. ZCómo son las circunferencias del Ítem b? iY las del ítem c? ipor qué?
28.
Unan con flechas las respuestas correctas.
a. La cuerda más larga de una circunferencia es...
b. El arco es una parte de...
c. Una cuerda divide al círculo en dos...
d. La distancia del centro a la circunferencia es...
e. Et diámetro es el dobte det...
f. Los radios unen un punto de la circunfeiencia con...
g. Si se unen dos semicircunferencias se forma...
h. El interior de [a circunferencia es...
29. Marquen en [a circunferencia los elementos que se indican.
a. El radio y el diámetro. ZCuánto miden?
b. Un ángulo central de 60o.
c. Un ángulo central de 2100.
d. Una cuerda de 2 cm y marquen con distinto color
los arcos que córresponden a la cuerda.
... radio.
... el diámetro.
... el círculo.
... la circunferencia.
... el radio.
... arcos.
... el centro.
... la circunferencia.
ffiffiHBHHnnt
Construcción de circunferencias
Se pueden construir circunferencias a partir de diferentes datos sin utilizar una regla graduada.
' Dado el radio: se toma la medida del radio con el compás, se pincha en el centro y se traza
la circunferencia.
Dado el diámetro: se encuentran el centro y el radio trazando la mediatriz del diámetro y luego
se dibuja la circunferencia con el método anterior.
'
I
o Dada una cuerda, se pueden seguir estos pasos.
)
fueden repasar
como se tr¿za um
mediariz en la
pigina 95.
(mediatriz de ab)
t. Se traza [a mediatriz de [a cuerda y sobre e[[a se marca
un punto o cuatquiera (excepto e[ que pertenece a [a cuerda) porque todos los puntos de [a mediatriz equidistan de
2. Se traza [a circunferencia de centro o que pasa por los
extremos de la cuerda. En este caso, se pueden trazar infinitas circunferencias según e[ centro etegido.
sus extremos.
.
Dado un arco de circunfurencia, se pueden seguir estos pasos.
1.5e marcan tres puntos sobre e[ arco yse trazan [as dos
cuerdas que los unen. Se traza [a mediatriz de cada una. E[
2.5e pincha e[ compás en o yse traza [a circunferencia que
pasa por tos puntos marcados sobre e[ arco.
punto de ¡ntersección de las mediatrices (o) es e[ centro de
la circunferencia.
1. Respondan y expliquen las respuestas.
a 5i se conoce el diámetro de una circunferencia, ise puede construir una única circunferencia?
b. A partir de una cuerda, ise puede construir una única circunferencia?
c Si se conocen dos cuerdas consecutivas, zes posible construir la circunferencia?
r II
tflYllltt:de
30.
circunrerencias
Construyan en cada caso una circunferencia que cumpla con las condiciones dadas.
c
./
b. nrn diámetro.
31. Construyan una circunferencia que
cómo lo pensaron.
8.
d. G
arco
paÉe por los vértices de las siguientes figuras. Expliquen
b.
ffiEBEEEnBt
Polígonos
Se llama polígono a toda figura que tiene tres o más lados.
Ctasificación según sus ángulos:
Go¡rvexo: cuando todos sus ángulos interiores
son menores que 180o.
Clasificación según sus lados:
Reguhr: cuando todos sus [ados y sus ángulos
son iguales.
Clincavo: cuando atguno de sus ángulos inte-
lnegular: cuando uno de sus lados o de sus
ángutos es distinto a los demás.
Elementos del polígono:
Diagonak es elsegmento gue tiene por extremos un vértice a otro no adyacente a é1.
. Apotema (Ap): es el segmento perpendicular
.
al lado del polígono cuyos extremos son el
.
ángulo central
punto medio del lado y el centro del polígono.
Angulo centraL es el ángulo cuyo vértice es
el centro del polígono.
La suma de los ángutos interiores de un potígono es:
18ü . (n - 2),
En un hexáqono (n =
donde
n es [a cantidad de tados.
6) la suma de loe óngulos
.interiores es 1 BOo . (6 - Z) = 7 2Oo.
9i la suma de loe ángulos inlnriores de un Volíqono es 54oo , ¿cuánÍoe ladoe liene?
lBOo.(n-Z)=54Oo
n-2=54O":18O"
n=3 +2
11
=
5
Entonces, el Volígono ea un pentágono.
1. Respondan y expliquen las respuestas.
a. Un polígono irregular, Zpuede tener tres lados iguales?
b. un polígono convexo, ipuede tener una diagonat que no pase por su interior?
c. ZQué triángulo y qué cuadrilátero son polígonos regulares?
d. El ángulo central de un polígono regular, Zpuede medir g0o?
Curso:-
Fecha:-/-
: lt+ ff1,'Ji3f3*
32. Midan los ángulos de los siguientes polígonos y
FIGURA A
respondan.
FIGURA B
a. Clasifiquen los polígonos según sus lados y según sus ángulos.
b. Calculen [a suma de ángulos interiores de cada uno de los potígonos. ZCómo son los resultados?
c. Tracen las diagonales desde uno de los vértices en cada uno de los polígonos. ZCuántos triángulos se forman? aSe puede relacionar la cantidad de triángulos que quedan formados con la
suma de los ángulos interiores?
33.
Calculen la amplitud de los siguientes ángulos.
a. Datos:
á:8x+12o
b:7x+35o
^t
'i=153o-x
d=8x-13o
é=6x-1o
c. Datos:
ñ=53o-x
ñ=10x+3Oo
6=x+4o
P:¡x
f:3x+38o
b. Datos:
0=4x-10'
d. Datos:
? :4x-7oo
h = 5x-640
A:2x+15o
i:3x+160
i =2x-4o
k:8x+Lo
ü=3x-25o
0=x+20o
t=x-1o
t:go"
v
HBEESgEE
Construcción de polígonos regulares
Para consÍt¡ir un penEgono regular con compás, regla y transportador,
pueden seguir estos pasos.
1. se dibuja una circunferencia y
un
ánguto
"
radio. Se calcuta e[ vator del
centrat_oétp_otigono haciendo
360" :5
=72".
2. A partir det radio de [a circunferencia y tomando como vértice e[ centro,
;tóuujrn ,in,o
del2.
ángutos
.r*.riiuól
3. Los puntos en donde se cortan los
lados de los ángutos con [a circunferencia son los vértíces det pentágono.
se puede conshuir un polígono regular a partir de un triángulo isósceles. para
ello, la medida
del ángulo desigual det triángulo debe ser divisor de 3600.
Por ejemplo, dado un triángulo isósceles con el ángulo desigual
de 45o, se puede realizar la
siguiente construcción.
1. Se traza [a circunferencia tomando
c0m0 centro e[ vértice del ánguto desigual y como radio uno de los lados
iguales.
2. 5e toma con e[ ibmpás ta medida
del tado desigual del triánguto y se
marca sucesivamente en [a circunferencia comenzando en uno de los vértices det triánguto que íntersecan a [a
circunferencia.
3. Se determinan los segmentos que
son lados det potígono regutar. Et potígono obtenido en este caso es un
octógono.
1. Respondan y expliquen las respuestas.
a. iEs correcto decir que e[ ánguto central de un eneágono regular
mide 40o? ieué cálculo se
debe realizar?
b' Si se conoce el ángulo central de un polígono regular, Zse puede averiguar
la cantidad de
lados que tiene? ZCómo?
c' Si se unen el centro de un pentágono regular con cada uno de los vértices,
ien cuántos
triángulos isósceles se lo puede dividir?
d. A partir de un triángulo escaleno, ise puede construir un polígono regular?
r l5
34.
tflLYllltTde
porígonos resurares
Completen sabiendo que los polígonos son regulares.
35. Construyan los siguientes polígonos
a.
Cuadrado.
i^ii
i/
regulares.
c. Eneágono.
Lii
\ii
/
-
b. Hexágono.
L_*
\
l5
ACNV¡DADES
Construcción de polígonos regulares
36. Escriban V (Verdadero) o F (fabo) según corresponda. Exptiquen las respuestas.
a.
)
Et ánguto central de un potígono regular de 20 lados mide 18'.
[-l
b. Para construir un triángulo equilátero se debe trazar un ángulo centraI que mida
c. A partir de un triánguto equilátero se puede construir un polÍgono regutur.
d. Para calcular et ángulo central de un polígono de 15 lados se resuelve
60".O
[-l
360o
:
tt.C
e. Los lados de un polígono regular son cuerdas de una circunferencia.
f.
Para construir un polígono regular se debe conocer [a medida de un ángulo
interior.[-l
37. Ubiquen el centro, el radio, la apotema y la circunferencia que pasa por los vértices de cada
potígono. Expliquen cómo lo pensaron.
b.
)
38. Construyan un octógono y un dodecágono con regla y transportador.
Expüquen cómo lo pensaron.
*-*"-****t
{
rls
ACTMDADES
Construcción de polÍgonos regutares
39. Construyan un polfgono a partir de los siguientes triángulos, cuando sea posible. Luego escriban el nombre del polígono construido.
a.
c.
V
i
I
I
L
menteACT|VA
Mariano fue a una granja y vio cómo tas abejas construían su panal. Se dio
cuenta de que cada una de las celdas tenía forma de hexágono, y que cada
celda compartía sus lados con la celda vecina, sin dejar espacios vacíos.
a. ZEs posible construir un panal con otras figuras geométricas que no sean hexágonos? Si
fuera posible, Zqué polígonos usarían?
b. Diseñen en sus carpetas, dos posibles panales teniendo en cuenta las siguientes opciones:
o Usando un polígono regular de más de seis lados.
. Usando dos polígonos regulares distintos.
I
(
lnrrEHArlún
40.
Resuelvan.
Eugenia compró un nuevo compás y para probarlo realizó las siguientes figuras.
FIGURA A
Jt.33.J¡+.lS
42. Copien las siguientes figuras en sus carpetas y luego, tracen la circunferencia que pasa
por los vértices de cada una de ellas. Expliquen
cómo lo pensaron.
a.
b.
43.
Resuelvan.
a. iQué elementos del cuadrado permiten trazar
una circunferencia que pase por sus vértices?
a. Según su posición, icómo se clasifican las
circunferencias de cada figura?
b. Copien las figuras en sus carpetas.
b. iEs posible trazar una circunferencia que
pase por todos los vértices de un trapecio
Expliquen cómo 1o realizaron.
rectángulo? iPor qué?
c. Los puntos de la figura B, iestán alineados?
41. Construyan teniendo en cuenta las indicaciones dadas en cada caso.
a. Una circunferencia cuyo radio mida 2 cm.
b. Marquen los puntos b y c. Luego, tracen
una circunferencia con centro en c de modo
que b sea un punto interior.
c
Marquen los puntos d y e. Luego, tracen una
circunferencia con centro en e y que pase por d.
d. Marquen los puntos f y g. Luego tracen
una circunferencia que contenga a f y no a g.
e. Tracen el ñi y luego una circunferencia que
tenga al segmento como cuerda.
f. Tracen et jT y una circunferencia, de modo
que el segmento sea su mayor cuerda.
44. Construyan los polígonos.
a. Un pentágono regular cuyas diagonales
midan 5 cm.
b. Una circunferencia a partir de una cuerda
de 3,5 cm.
c. Un hexágono regular a partir de un triángulo equilátero de 3 cm.
45. Construyan los siguientes polígonos teniendo en cuenta los datos.
a. Es regular, el ángulo central mide 60o y es
convexo.
b. Es regular, tiene en total cinco diagonales y
la suma de sus ángulos interiores es de 5400.
c. Comparen los gráficos con sus compañeros.
ila solución es única? ipor qué?
46. Construyan y luego, respondan.
fl8. observen tos polígonos y
respondan.
* Triángulo equilátero.
.
Cuadrado.
', Pentágono regular.
"
Hexágono regular.
a. Tracen todas las diagonales que tienen
cada uno de los polígonos construidos y
completen [a tabla.
,\]
ti
r.i
!:
Triángulo
F
\\
f
¡
¡
!
-'g?
l
i
J
L-*_._.-.
Hexágono
b. iCuántas diagonales tiene un heptágono?
iY un octógono? Expliquen cómo lo pensaron.
47. Escriban V (verdadero) o F (rabo).
Expliquen [as respuestas.
a. Una cuerda es un segmento que une dos
puntos de la circunfer.n.ia. [-l
b. En un polígono regular, los lados y los
ángulos son iguales. [-l
c. E[ ángulo central de un octógono regular
mide 45". [-|
d. La suma de los ángulos interiores de un
,-l
polígono es 412o.
I
r
e. El círcuto es e[ contorno de la circunferencia.
[-l
g. Un rectángulo es un polígono r..gufur. [-l
h. El ángulo central de un triángulo equilátero
mide 120'. [..l
i. Un pentágono puede dividirse en cuatro
triángulos al trazar las diagonales desde uno
[--l
de sus uerti..s.
i. El decágono es un polígono que tiene doce
(-l
k. Para calcular el ángulo interior de un poli
gono regular, se debe dividir 360o por la cantidad de taOos.
a. Clasifiquen los polÍgonos en cóncavos y
convexos.
b. iCuántas diagonales tiene cada polígono?
c. Si dos polígonos tienen la misma cantidad
de lados, itienen la misma cantidad de diagonales?
49. Compteten con "siempre", "a veces" o
ttnuncatt.
a. Un cuadrado
rectángulo.
b. Los pentágonos, hexágonos y octógonos,
son regulares.
c. Un rectángulo
un cuadrado.
es
es posible que un
polígono regular sea cóncavo.
d.
f. El radio es el doble del diámetro.
tados.
l
"***.***-l
[-l
50. Lean atentamente y averigüen de qué potígono regular se trata en cada caso. Luego, cal'
culen la medida del ángulo central.
a. Desde uno de sus vértices se pueden trazar solo 12 diagonales.
b. La suma de sus ángulos interiores es 9000.
c. Es un polígono que no tiene diagonales.
d. Es un polígono que tiene el doble de
lados que e[ polígono que tiene un ángulo
central de 72o.
e. Su ángulo central mide el doble de 20o.
AuroEvALUActón
51. Construyan las siguientes figuras.
a. Un triángulo isósceles cuyos lados iguales
midan 4,5 cm y el ángulo entre e[[os mida 50o.
c. Un rombo cuya diagonal mayor mida 5 cm,
su diagonal menor mida 3 cm y uno de sus
lados mida 4 cm.
*-"*l
t
I
i
f
T
I
I
i
¡
I
i
I
I
i
I
j
!
b. Una circunferencía a partir de [a cuerda mn.
d. Un polígono regular a partir del siguiente
triángulo isósceles.
I
¡
i
I
I
I
I
I
!
\
¡
I
I
'.
i
L
52. Calculen los ángulos interiores.
a. Datos:
A :12x- 74o
t:9x+15o
"N
9=7x+99"
b. Datos:
fi:¡*
ñ:5x-16o
o:x
c. Datos:
?:8x+2"
A=o*
t : 22x- !4o
0:3x-6o
,ry
Slrulclór tilrcrAl
DE APRENDTzAfE
1. Observen la imagen y respondan.
a. Las siguientes son algunas de las preguntas que realizó un interesado por uno de los departamentos con las respuestas que recibió.
. Si quisiera colocar una guarda en las paredes, icuántos metros necesitaré? 24 m
. iE[ largo y el ancho coinciden? No.
. Si quisiera ubicar un mueble de 5 m de largo, ipuedo hacerlo sobre cualquiera de las paredes? lVo.
6obre qué departamento realizó la consulta? ZCUáles son sus dimensiones?
b. Si hubiese preguntado por el otro departamento, Zcuáles serían las respuestas?
SEEnnmnn
PerÍmetro y área de figuras planas
Medir una longitud signífica compararla con otra considerada como
unidad de medida.
,¿-"\ hm
ú-,r\,Á"\,
dam
km
m
decómerro melro
\i/vvv\/\/
kilómetro hectómeÍro
/-..r\ cmf..r\
dm
decímetro cenlímeÍro
mm
mílíme?ro
Pefmebo y área
El perímeho de una figura es igual a la suma de las medidas
de todos sus lados. para calcular
el perímetro, todos los lados deben estar expresados en la misma unidad
de medida.
se llama área a la cantidad de veces que entra en una superficie la
unidad de medida elegida.
Un cuadrado de 1 melro deladoÍiene un áreaigual a 1 m2.
lr+lr+1,
B+b+lr+1,
2 . lr+ 2 . l,
2 . lr+ 2 . l,
2'.lr+2.1,
1. Respondan y expliquen las respuestas.
a. ZCómo se calcula el perímetro de un triángulo equilátero con una
multiplicación?
b' si se divide un rombo por sus dos diagonales, ise obtienen cuatro
triángulos de igual
área? LY si es un romboide?
c. 6e puede calcular el área de un cuadrado teniendo como dato perímetro?
el
d. ZQué figuras tienen la misma fórmula del perímetro? iy el área?
Curso:-
Fecha:_/:_
rlE
ACÍIVIDADES
Perímetro y área de figuras planas
1. Escrlban V (Verdadero) o F (Falso) según conesponda. En caso de que sea F, escriban la respuesta conecta.
a.45 hm:45oOO
b. O,O54 m = 5,4
rC
d.7,2
rt O
dam
= 0,72
e. O,727 hm
f.32 cm:
c.3,18 dm = 0,00314 f<m !
:
nt
O
7 210 cm
0,0032
A.r [--.)
2. Calculen y escrlban el resultado en cm.
a. El perímetro de un rombo de 30 mm de lado.
b. El perímetro de un rectángulo si uno de sus lados mide 0,2 dm y el otro mide el doble.
c. La longitud de cada lado de un triángulo equilátero, si su perÍmetro es 0,15 m.
d.
Et perÍmetro de un cuadrado de 0,6 dm de lado.
e. Los lados de un romboide sabiendo que su perímetro es de 32 cm y el lado mayor es el tripte det menor.
3. Calculen el perfmetro de las siguientes figuras. Escdban el resultado en
a.
cm.
C.
12 cm
20 mm
0,000021 km
d.
b.
0,15 m
80 mm
1,2 dm
]E
ACTMDADES
Perímetro y área de figuras planas
4. Completen según corresponda.
a.3,2 m2:
b. o,oo5 hmz
)
o',
d. 0,0042 hm2 + 0,5 dam2 :
E
ou''
or,
f]--]
: [-]
f]]]]
c.3 cm2=
5. lndiquen cuántos cuadrados de área tienen las siguientes figuras.
r.!
'.c
..c
\
-
\
)
/
\
6.
Rodeen con color la respuesta conecta.
a. iCuál es el perímetro de un cuadrado de 9
dm
1,2
)
r'
cm2
de área?
36 cm
t2 cm2
b. Si en un rectángulo, la medida de la base y de la altura son números consecutivos y su perímetro es 18 cm, Zcuál es su área?
81
cm2
2O
cm2
c. iCuál es el perímetro de un círculo cuya área es7,O65
7,065
dm
9,42
dm
90
cm2
dm2?
!4,7 m
d. Si la base y la altura de un paralelogramo son iguales a las de un triángulo de área 75
icuál es su área?
)
30
cm2
7,5
ninguna de las anteriores
cmz
7. Calculen.
a. La base de un rectángulo de perímetro 30 cm y altura 6 cm.
b. La base de un triángulo de área 72
)
cm2
y altura 3 cm.
c. El radio de un círculo de perímetro 72,56 cm.
cm2,
rlE
ACTIVIDADES
Perímetro y área de figuras planas
8. Calculen
el área y el perímetro de las siguientes figuras.
ab.
8cm
"l -.'
perímetro
Área
: t-l
ll
Perímetro =
: f-l
Área =
9. Calculen el área
¡LC
(-l
sombreada de las siguientes figuras.
f
r---------!-!!----"-*r
5cm
1cm
Área sombreu.u
:D
Área sombrero. =
f--]
d.
Área sombreu.u
10.
:D
y resuelvan.
a. E[ área de un pentágono es de7,5
Área sombreuou =
f--l
Lean atentamente
dm2. Si la apotema mide 30 mm, Zcuánto mide
el lado?
b. Si at área de un rectángulo de 15 cm de base, se le resta el área de un pentágono de 80
se obtiene 55 cm2. ZCUánto mide la altura del rectángulo?
lF
cm2
menteACflVA
I o. una masa rectangular de 30 cm de largo y 20 cm de ancho se cortan círculos de 5 cm de
I radio para preparar empanadas, de modo que se aproveche la mayor cantidad de masa posible.
a. ZCuántas tapas de empanadas satdrán? iCuántos cm2 de masa sobran?
I
b. 6e pueden cortar más tapas con la masa que sobra? iCómo?
t
I
EEsEFnnnl
Area lateral y total de prismas, pirámides y cilindros
de un poliedro es la suma de las áreas de todas las caras laterales.
total de un poliedro es la suma de las áreas de todas sus caras.
Et área lateral
E[ área
Area del prisma
:
perímetro de [a base . altura
Área total = área lateral + 2 . área de la base
Área lateral
=sl
)
Area de la pirámide
L
. .
Área totat :
nt gq
perímetro de la base . altura de la cara lateral
lqLgt ol
2
área lateral + área de la base
)
Area del cilindro
Para calcular e[ área lateral de un cilindro, se debe calcular el área del rectángulo que forma su
parte lateral.
La base del rectángulo coincide con la longitud de la circunferencia de [a base del cilindro.
)
Área lateral
Área total
:
:
área del rectángulo: b
área lateral + 2 . n . 12
.h:2.n.r.h
1. Respondan y expliquen las respuestas.
a. Si un prisma de base triangular y un prisma de base cuadrada tienen la misma altura, iel
área total es la misma?
b. La diferencia entre el área total de una pirámide y su área lateral, Zes el área de la base?
c Si se conoce el área total de un cilindro, ise puede calcular el área de la base?
d. Para empapelar la columna de una habitación, ase debe calcular su área total?
I 17 t*tfáli:r totar de prismas, pirámides y cilindros
11. Unan con flechas los nombres de los cuerpos con sus conespondientes áreas laterales y totales.
Cuerpo
Area taterat
Area totat
Prisma de base triangular regular
o12.4
.Árealateral
Cilindro
ob.h.3
'o
Cubo
Pirámide de base rectangular
Pirámide de base heptagonal regular
rn '7
o2.n.r.h
.'r'rnr.r*
br.h,
2'
+2.n.Í2
. Área lateral * o )n . z
. Área lateral + 12 . 2
. Área lateral + Per . Ap : 2
. Área lateral + b. h . 2
12. Calculen el área lateral y el área total de los siguientes cuerpos. Pueden ayudarse realizando
una figura de análisis de los desanollos conespondientes.
c. Cilindro.
a. Prisma de base cuadrada.
2cm
10 cm
H
5cm
4cm
b. Pirámide de base cuadrada.
d. Pirámide truncada de base cuadrada.
13. Resuelvan.
Sofn quiere cubrir cinco macetas con forma de prisma de base rectangular de 0,5 m de largo, 2 dm
de ancho y 3OO mm de alto, con venecitas cuadradas de 3 cm de [ado. Si solo debe cubrir los laterales, icuántas venecitas necesita?
tl t
I I
AcrrvrDADEs
Área lateral y total de prismas, pirámides y cilindros
14. Calculen el área latenl y el área total. Escriban el nombre del cuerpo al que pertenece cada
desanollo.
7cm
Area lateral:
Area lateral:
Area totalt
Area total:
Nombre:
Nombre:
b.
Área lateral:
Area lateral:
Área total:
Area total:
Nombre:
Nombre:
15. tean atentamente y calculen. Escdban el resultado en dm2.
a. El área lateral de un prisma de base rectangular, si las medidas de su base (en dm) son dos
números impares y múltiplos de 3 comprendidos entre 8 y 18 y su altura es 10 cm.
b. El área total de un cilindro si el ndio y la altura son dos números consecutivos, cuya suma es 15 cm.
c. E[ área lateral de una pirámide de base cuadrada si la altura de sus caras es la mitad de la
medida del lado de la base, sabiendo que el área de la base es 16 cm2.
I 17 t*"fr*,*,
totat de prismas, pirámides y citindros
16. Calculen el valor de ta incógnita.
a
b. Datos:
Datos:
Área total :
62
Todas las aristas miden lo mismo.
cm2
Área total
:
2200
mm2
17. Resuelvan.
Una empresa hbrica dos tipos de carpas. ZCuántos m2 de lona se necesita para cada una de ellas?
b.
\'
-"L---'--
],'
l&
Respondan.
Pedro quiere pintar eltanque de agua de su casa, de forma cilíndrica, de 2 m de diámetro y 3 m de alto.
a. Si la pintura rinde 1 m2 por cada medio litro, icuántos litros serán necesarios?
b. Si el balde de 5 I cuesta $80, icuántos baldes deberá comprar? ZCuánto gastará en total?
19. Resuelvan.
las paredes de su cochera de 3 m de largo, 2 m de ancho y 2,5 m de
alto con listones de madera de 1 m por 5 cm. iCuántos listones necesitará?
a Agustín guiere cubrir
b. Cada cara de un cubo mágico se compone de 9 cuadrados de 20 mm de lado. Si se quieren
construir sus caras en acrílico, icuántos cm2 serán necesarios?
HEnnEnEn
)
Unidades de capacidad y unidades de volumen
cÉ
t¡.Mbl¡nb¡ a tsAR
q'E oütf,uü ü.ERb¡¡EL
Se llama volumen a[ lugar que ocupa un cuerpo en el espacio
y capacidad a aquello que puede contener.
Unidades de volumen
un metro cúbico es el volumen que ocupa un cubo de un metro de arista.
Un decímetro cúbico es el volumen que ocupa un cubo de un decímetro de arista.
Para armar 1 m3 son necesarios 1000 dm3.
)
Para pasar de una unidad de volumen a otra que sea su inmediata inferior, se debe multiplicar
por 1000 y para pasar a su inmediata superior, se debe dividir por 1000.
kilómetro cúbico
km3
hectómetro cúbico
decámetro cúbico
hm3
dam3
decímetro cúbico
centímetro cúbico
milímetro cúbico
dm3
cm3
mm3
1000000000 m3
1000000 m3
1000 m3
0,001 m3
0,000001 m3
0,000000001 m3
Unidades de capacidad
La capacidad de un cuerpo se mide.en litros.
/'1;ñ\ a.,^,
avar,\/cv
kl
hl
dal't
kilolilro hecÍolitro decalitro
\r'\/\i/\/\/V
lírro
dlctmt
decíliiro centilítro
La siguiente tabla muestra las equivalencias entre las unidades de volumen
1. Respondan y expliquen las respuestas.
a Para pasar de cm3 a m3, Zqué cálculo se debe realizar? Zy a mm3?
b. iEs cierto que 1 kl equivale a 100 litros?
c Para llenar un tanque, zes lo mismo saber el volumen que la capacidad?
mililil';ro
y las de capacidad.
I]E
20.
ACNUDADES
Unidades de capacidad
gscriban
a,2
mr
:
V
(Verdadero) o F (Falso) según conesponda. En caso de que sea F, conijan el enor.
200
r'
d. 0,540 dm3 - 40 cm3 = 0,5 Art
cm3
b. 0,000034 hm3
c. 4200
y unidades de volumen
:
34
O
e. 0,06 dam3 + 55 cm3 = 0,01 aamt [-l
m
. 0,5 hm = 2100
f. 3 cm'z .7,2 cm + 0,004
dam3
dm3
= l,e+ cm, [-..]
21. Completen las siguientes equivalencias.
a. 250 .,n, =
[-]
1OOO.r':
D
:
c.32 dl D.r'
b.
22.
t
t
d. 0,00018 m3 =
I
e. 280 dl =
r. 135kI
:Dor'
Resuelvan los siguientes problemas.
a. Para su fiesta de cumpleaños Pablo compró botellas de gaseosa de 2,5 l. Si tiene 40 invitados
y calculó 3 vasos de 300 cm3 por persona, Zcuántas botellas de gaseosa compró?
b. En un supermercado ofrecen tres botellas de aceite de la misma calidad. La primera es de
750 cm3 y cuesta $15, la segunda es de 1 I y su costo es de $t8 y la tercera es de 500 cm3 y
cuesta $fz. ¿Cuál conviene comprar?
c. Matías prepara un licuado con 500 cm3 de leche, f, titro de pulpa de frutillas y 200 ml de
pulpa de durazno. ZPodrá colocar la preparación en una jarra de un litro? iPor qué?
d. Ana prepara un perfume para sus dos mejores amigas mezclando
alcohol, 120 cm3 de
esencia de jazmines y 5 cl de agua. Si los frascos que consiguió tienen una capacidad de 80 m[,
$ta"
Zcuántos frascos puede llenar?
ile
sobra perfume?
e. Para el mantenimiento de la piscina de un club, se le debe agregar cloro al agua semanalmente. Si la piscina tiene una capacidad de 138 kl y por cada 10 m3 de agua se debe agregar
medio litro de cloro, icuántos litros por semana son necesarios?
menteACTlvA
Las equivalencias entre unidades de capacidad y de volumen pueden
servir, por ejemplo, para averiguar el volumen de una piedra. Si se dispone de un vaso medidor lleno de agua, cuya capacidad es de 500 ml, y
de una piedra que cabe dentro de ese vaso, icómo pueden hacer para
calcular el volumen de la piedra?
SEEEEEnEI
<
Volumen del prisma, de la pirámide, del cilindro y del cono
Volumen del prisma y de la pirámide
Volumen del prisma = área de la base .
Volumen del cubo
h
:
a3
a:aris'|affi]
ffi1"'*1ffi
\_,-a/
"
El volumen de un prisma es tres veces mayor que el volumen de la pirámide que tiene igual base
y altura.
.
.
1 área de la base h
'[a
ffit
Volumen de la pirámi¿e =
Volumen del cilindro y del cono
Volumen del cilindro = área de la base .
Volumen del cilindro =
fi.
12. h
h
área de E base
volumen del cono
-
Vofumen del cono
= t--4-=--h3
3
'
h
1. Respondan y expliquen las respuestas.
a. El volumen del cubo, ise puede calcular utilizando la fórmula del prisma de base cuadrada?
b. Si un cono y un cilindro tienen la misma base y altura, ies cierto que el volumen del cilindro es el triple que el del cono?
Curso:-
Fecha:-/-
I I 5
23.
i:llYl3f?t?
o,,rma, de la pirámide, der cirindro y der cono
Calculen el volumen de cada cuerpo. Escriban el resultado en cm3.
d.
a.
4cm
e.
b.
A
7cm
Al::
¿ü
--
0,6
.n,'-
3cm
C.
l..'
2cm
A
12 mm
0,3 dm
]T
ACTIVIDADES
Votumen del prisma, de la pirámide, del cilindro y del cono
24.
Completen el siguiente cuadro conespondiente a prismas de base rectangular.
25.
Calculen la capacidad de los siguientes cuerpos. Expresen el resultado en litros.
)
a.
b.
A
)
A
60 cm
700 mm
--_J d,
-
360 mm
)
26.
Resuelvan.
a. Completen la siguiente tabla con e[.volumen correspondiente a cada cilindro.
)
!2,56
cm3
b. Observen la tabla y completen.
)
. Si e[ radio se duplica, el volumen .t f]
. Si e[ radio se triplica, e[ volumen C
"r
. Si la altura se duplica, el volumen .r O
. Si la altura se triplica, e[ volumen C
"t
veces mayor.
veces mayor.
veces mayor.
veces mayor.
rlr
27.
ACÍIVIDADES
Volumen del prisma, de ta pirámide, del cilindro y del cono
Calculen lo pedido en cada caso, teniendo en cuenta los siguientes datos.
a. Prisma de base rectangular
c. Cono
4 cm
Ancho: 3 cm
La altura es igual a la mitad del largo.
Diámetro de la base
Altura : 8,5 cm
Largo :
Volumen
: f-l
Votumen
b. Cilindro
Diámetro de la base
Volumen
Attura
28.
:
:747,3
:
6
:
:
6 cm
t-l
d. Pirámide de base cuadrada
Altura = 10 cm
Volumen : 30 cm3
cm
cm3
f-l
Lado de la base
:
Calculen el volumen de los siguientes cuerpos.
a.
b.
2cm
6cm
29.
Resuelvan las siguientes situaciones problemáücas.
a. En una caja rectangular de 8 dm de largo, 60 cm de ancho y 1 m de alto se quieren colocar
velas de 20 cm de diámetro y 50 cm de altura. ZCUántas velas se pueden colocar? iQué volumen
de la caia queda vacío?
b. Como souvenir de su fiesta de 15 años Leila construye pirámides de vidrio que rellenará con
arena de colores.. Si quiere construir 90 pirámides de base cuadrada de 5 cm de lado y 4 cm de
altura, icuántos cm3 de arena necesitará?
menteACT|VA
r
cm3
de oro pesa 77,4 g, icuántos
l: 0,15 m
b: 0,65 dm
rB:8cm
r h: 400 mm
(g
pesa el lingote de oro?
COilTEilIDOS
IntrEHAETún
30.
JE.J7.3E.3S
32.
Calculen.
a. El perímetro de un paralelogramo de área
igual a 20 cm2, si la altura es 4 cm y sus
otros lados miden J de la base.
b. El perímetro de un trapecio isósceles, si
el área es de 30 cm2, la altura es de 4 cm y
cada uno de los lados iguales mide 6 cm.
c. El área de un romboide cuyas diagonales
son dos números primos que al sumarlos se
obtiene 15.
d. El área de un trapecio de base mayor igual
6 dm, base menor igual a ] ae U base mayor
y altura igual a la diferencia entre la base
mayor y menor.
e. El área de un cuadrado de lado igual al
Calculen el área lateral y total de cada uno
de los siguientes cuerpos.
a.
3cm
b.
H
O
ffi
diámetro de un círculo de área 3,74 m2.
4dm
l--J
1O dm
31. Calculen el área sombreada en cada caso.
a.
+
b.
6cm
?
1,.'
33.
Resuelvan las siguientes situaciones pro-
blemáticas.
a. Se desea colocar etiquetas alrededor de
20 ftascos de mermelada de 6 cm de diámetro e igual altura. iCuántos cm2 de papel
C.
6cm
d.
8cm
serán necesarios?
b. Se quieren construir cinco cubos de 50 cm
de arista para un juego didáctico. ZCuántos
m2 de cartón serán necesarios?
c. Manuel quiere cambiar el piso y las paredes de su baño, de 1,5 m de ancho y 2 m
de largo y 3 m de alto, colocando cerámicas
cuadradas de 25 cm de lado. Si cada caja
contiene 20 baldosas, Zcuántas caias deberá
comprar?
Curso:-
Fecha:-/-
Una jarra contiene 1 litro de agua y a[ colocar en
ella un cubo de plástico se derramaron 64 m1.
a. iCuánto mide la arista del cubo?
b. Si se colocan nueve cubos más en la
misma jarra, iqué volumen de agua quedará?
Escriban la respuesta en cm3.
35.
Resuelvan.
a. Si el volumen de un cubo es de 0,064 dm3,
Zcuánto mide [a arista?
b. Si la altura de un cilindro mide 6 cm y su
radio es igual a J O" t, altura, Zcuá[ es el
volumen?
c. El volumen de una pirámide cuya base es
un hexágono regular es de 67375 mm3. Si la
altura mide 0,7 dm y e[ lado de la base mide
Una nueva fragancia de perfume será envasada
3,5 cm, Zcuánto mide la apotema?
en frascos de forma piramidal con base cuadrada de 9 cm de lado y 72 cm de altura.
a. Si se quieren envasar 32 litros de perfume,
d. Si el volumen de un cono es de 42,39
y e[ radio de la base mide 3 cm, ácuánto
mide la altura?
cm3
Zcuántos frascos serán necesarios?
b. Si se quiere colocar de a nueve frascos en
cajas cuadradas sin apilar, Zqué dimensiones
39.
Calculen el volumen en cada caso.
debe tener cada caja?
0,3 m
36.
Piensen
y resuelvan.
a. Para festejar el Día det Estudiante, los chicos
llevaron a [a escuela gaseosas para compaftir.
En total había tres botellas de 2,25litros, dos
de 1000 cm3 y cuatro botellitas de 600 cm3. Si
cada alumno tomó dos vasos de
f
litro, apara
4dm
volumen =
f---]
o',
b.
cuántos alumnos alcanzó la bebida?
60 cm
b. Nicolás debe llenar frascos de forma cilíndrica de 6 cm de diámetro y altura igual a
f aef radio de la base con dulce de teche. Si
cada bolsa contíene 47,'J. cmj de dulce de
leche, Zcuántas bolsas serán necesarias para
llenar 12 frascos?
c. Se quieren fabricar conos de 50 cm de diámetro y 90 cm de altura para señalizar un
camino. Con 2 m3 de plástico, Zcuántos conos
pueden fabricarse?
d. Si el volumen de una pirámide de base
cuadrada es 45 cm3 y su altura es 5 cm,
Zcuánto mide el lado de [a base?
37.
Resuelvan.
Los caramelos de dulce de leche vienen enva-
sados en cajas de a 20, apilados en dos capas.
Las dimensiones de cada caramelo son 2 cm de
largo, 2 cm de ancho y 1 cm de espesor.
a. ZQué dimensiones tiene [a caja?
b. Si se duplican las dimensiones de la caja,
Zcuántos caramelos podrá contener?
Volumen
40.
: f].r'
Calculen en cada caso según corresponda.
a. Para llenar las J Rurt"r de un balde citíndrico de 24 cm de diámetro y 50 cm de altura, icuántos litros de agua se necesitan?
b. Si et área de la base de un cilindro es de
12,56 cm2 y el volumen es de 125,6 cm3, Zcuá[
es el área [atera[?
c. Si et área total de un prisma de base cuadrada es 38 cm2 y el área lateral es de 13 cm2,
icuánto mide e[ lado de la base?
d. En una pirámide de base pentagonaI regular, e[ lado de la base mide 4 cm y [a apotema,2,5 cm. Si e[ área total es 75 cm2, Lcuál
es el área de cada una de las caras?
AuroEvALUAclón
41. Completen.
a. El perÍmetro de una figura es igual a
la
b. La fórmula del área de un paralelogramo
de todos sus lados.
a la fórmula del área de
es
un rectángulo.
c
La fórmula para obtener el perímetro de cualquier figura regular de n lados de longitud /
es
d. El área lateral de un cilindro de diámetro d y altura h es
e. El área total de un cubo es
42.
Respondan.
Alrededor de una cancha de fútbol se colocan publicidades utilizando lonas de g0 cm de ancho. Si
la cancha mide 100 m de largo y 80 m de ancho, icuántos m2 de lona se necesitarán?
43.
Resuelvan.
Agustín acomodó su cuarto como se ve en el
siguiente plano. iCuántos m2 le quedaÉn libres
pan
circular?
2,5 m
100 cm
44.
meea deluz
Resuelvan las slgulentes sltuaclones problemádcas.
a. Naty prepara conos rellenos de mousse de chocolate para una fiesta de 100 invitados. Si los
conos tienen 6 cm de diámetro y 0,08 m de altura, icuántos litros de crema necesita? Escriban
la respuesta aproximada al litro.
b. Para preparar pan se necesitan 400 ml de agua tibia por cada 750 cm3 de harina leudante. Si
se colocan esas cantidades en una máquina de amasar que tiene una capacidad de 1,25 dm3,
iqué volumen de la máquina quedará {ibre?
f,nntenlons
Variables, pobtación y
muestra.
Recolección y organización
de datos. Tablas.
Frecuencias absolutas y
relativas.
Gráficos.
Promedio, mediana y
moda.
Experimentos aleatorios.
Votan 200 alumnos.
Probabitidad simpte.
illtil0l'¡["
Cálculo combinatorio.
Alumnos
de secundaria
básica
Alumnos
de secundaria
superior
S¡rurc¡ór rilrcrAt DE ApREt{DtzAlE
1. Observen la imagen y resuelvan.
a. lnventen un enunciado con preguntas cuyas respuestas
'
120 alumnos.
, 80 alumnos.
b. Comparen los enunciados con los de sus compañeros.
sean:
40 alumnos.
,i
tt
$t
tá¡**"6rá¡¡ÉS
Variabtes, p oblación
muestra
-
Estadística
La Estadística se ocupa de [a recolección, organización y anátisis de datos para obtener determi-
nada información. Los datos se recolectan, en algunos casos, a través de encuestas y se los puede
organizar a través de tablas y gráficos para poder entenderlos y utilizartos mejor.
Población
y muestra
Se denomina población al coniunto de individuos (personas, animales, plantas, etc.) que se pretende estudiar estadísticamente. Cuando es diffcil estudiar toda [a población, se selecciona una
parte de ella denominada muestra. La muestra debe ser representativa, es decir, debe elegirse de
manera tal que del estudio estadístico se obtengan resultados muy próximos a los que se obtendrían con toda la población.
Variables estadísticas
Cada uno de los temas que se estudia de una población o
muestra se denomina variable estadística. Por ejemplo, si se hace
una encuesta para averiguar las alturas de los atumnos de primer
año, la variable es "altura de los alumnos de primer año".
cüAllb
Las variables se clasifican en:
" Cualitativas: se miden a partir de datos no
numéricos.
"Comida preferida delos alumnos de prlmer afio".
" Cuantitativas: se miden a partir de datos numéricos.
"Edad de loe jugadores de un equipo de fútbol"
.
tüA
E$ ¡.ixol E5IIN¡R
tA bD¡tbrl. GE.
HHn.
qírbt€?A@qE
q€¡.€,ccioNA
uA
E[rErtsu)A¡6r.k6Abrl
tobE. €ÉtErq¡AR trr|A
\¡sg5Rl"..
1. Respondan y expliquen las respuestas.
a. ZCuát es el primer paso del trabajo estadístico?
b. La población, ies parte de [a muestra?
c. Si se quiere conocer el lugar preferido para el viaje de egresados de los 80 alumnos del
último año (repartidos en 3 cursos), Zcuál puede ser una muestra representativa?
d. Una variable, ipuede ser cualitativa y cuantitativa a la vez?
r hn ii,'Jli*:lsour,.¡on
y
muestra
1. Marquen con una X el tipo de vadable en estudio.
La edad de los empleados de una empresa.
Cantidad de hijos de las familias de cierto barrio.
Buscador de lnternet que utilizan los alumnos de una escuela.
Modelo de automóvil más vendido durante el último año.
Peso de cada uno de los jugadores de un equipo de fútbol.
Película más vista durante el mes de febrero.
2.
Lean atentamente
y respondan.
Una empresa de programación de juegos para computadora quiere crear un nuevo producto. Para
ello, realiza una encuesta entre los usuarios, de entre 72 y 20 años, registrados en su sitio web
para saber qué tipo de juegos prefieren. Entre las opciones están los juegos de acción, de estrategia, de cartas, de búsqueda y de carreras. La encuesta fue respondida por 125 chicos de entre 12 y
14 años, 132 chicos de entre 75 y 77 años y 93 chicos de entre 18 y 20 años.
a iCuál es [a población a la que estará destinado el juego? iCuál fue la muestra?
b.
ZCuát es
la variable en estudio? Clasiffquenla.
y un ejemplo de variable cuantitatiüa que puedan
poblaciones.
Luego, propongan una muestra para cada población.
ser analizados en las siguientes
a. Un grupo de alumnos de 1.o año.
3.
Escriban un ejemplo de variable cualitativa
b.
E[ personal de una empresa.
c
Golosinas vendidas en los 200 quioscos de un barrio, en e[ transcurso de una semana.
l
tJ
Recolección
y organización de datos. Tablas
Para realizar un estudio estadístico, es necesarío usar una serie de henamientas y técnicas que permitan
recolectar la información necesaria. Entre los principales insür¡mentos de rccolección de dabs se encuentran
las encuestas, los cuestionarios, las entrevistas. También se puede recolectar información mediante la
observación directa o experimentos. Luego, los datos obtenidos se pueden organizar en tablas.
Las tablas se utilizan para mostrar información sobre [a relación entre dos
o más datos.
Enlahisfnria delos juegos ol(mpicos,la delegación argenlina obtuvo unfnfnl deTO medallas:
1B de oro,24 deplaray 2B debronce.El deVorEe quemósmedallaeobEuvo es elboxeo,con24.
En la siguienÍeÍabla se muestrala cantidad de medallas ohenidas según el deporfre.
Boxeo
24
7
7
10
34,3
Vela
9
0
4
5
12,9
Atletismo
5
2
)
0
7.1
Fútbol
4
2
2
0
5,7
a. ¿Qué datos a?arecen enlatabla?
La cantidad de medallas, eldeUlle deltipo
de medalla por deporte y el porcentaje de
cada uno sobre
eltotalde medallas.
Remo
4
7
1
2
5,7
Hockev
4
0
2
2
5,7
Tenis
4
0
1
3
5,7
Natación
3
L
L
I
4.3
depor\ee que ofuuvieron la misma canÍiddd demedallas?
5e tuvo en cuenta cuál deporte obtuvo
Polo
2
2
0
0
2.9
Básquel
2
1
0
1
2,9
Pesas
2
o
I
7
2,9
Ciclismo
7
T
0
0
7,4
Taekwondo
1
7
0
0
7,4
Equitación
7
0
1
0
7,4
Tiro
7
0
7
0
7,4
b. ¿Con
qué crilerio se ordenaronlos
más medallas de oro,luego más medallas
de plata y fínalmente, el que obtuvo más
medallas de bronce.
c. 5i se euman loe porcentajes de cada
Vótey
7
o
0
1
1,4
deporEe, ¿coincide con eltohal? ¿?or
Eserima
I
0
0
1
r,4
qué ocurre eslo?
Yudo
1
0
0
1
1,4
9íbien la euma de los porcentajes repreeenta el total de los datos (1 OO7), no
coincide porque los porcentajes de cada
deporte están aproximados a los décímos.
1. Respondan y expliquen las respuestas.
a. ZPara qué se escriben los datos en una tabta? ZQué información brinda?
b. A través de una tabla, ise puede saber de qué tipo es la variable en estudio?
c. En una tabla se sumaron los porcentajes y se obtuvo 99,6o/o, zpor qué ocurre esto?
r l+l
4.
ACTMDADES
Recolección y organización de datos. Tablas
Resuelvan.
Martín hizo una encuesta entre sus compañeros de colegio acerca de cuál es el club favorito de
fútbol de cada uno de ellos y obtuvo los siguientes datos.
River, River, River, Boca, Boca, Racing, lndependiente, Racing, River, Boca, River, River, Boca'
Boca, San Lorenzo, Huracán, Racing, lndependiente, Boca, San Lorenzo, Racing, San Lorenzo,
Gimnasia, Vélez, River, River, Boca, San Lorenzo.
a. Completen la tabla.
San Lorenzo
lndependiente
b. ZCuál es la variable en estudio? Clasifíquenla.
c
iCuál es el club con mayor cantidad de simpatizantes?
d. iCuántos clubes tienen al menos tres simpatizantes?
ZCuáles?
5. Completen la tabla y respondan.
El profesor de matemática está preparando un informe sobre los alumnos de primer año para presentar junto con ta planilla de notas. Las siguientes fueroh las notas obtenidas por los alumnos al
finalizar el año.
7O 9;
9;8; 8; 8; 5; 5; 4;4;
10; 8; 8; 6; 6; 6; 6; 8; 7; 7; 70; 9; 3; 6; 6; 6; 10;
5
a. Completen la tabla.
b. iCuál es la variable en estudio? Clasiffquenla.
c
iCuántos alumnos hay en e[ curso?
d. Si se aprueba con a[ menos 7 puntos, Zcuántos alumnos aprobaron? ZCuántos desaprobaron?
e. ZCuántos alumnos obtuvieron 8 puntos como mínimo?
f. Si ta nota obtenida está entre 4 y 6, los alumnos deben rendir la materia en diciembre y si es
menor que 4, deben rendir en marzo; Zcuántos alumnos deben rendir en cada instancia?
J
;¡
tJ
Frecuencias absolutas
it*-JL*J
relativas
Se denomina frecuencia absoluta (se escribe fl al número de veces que se repite cada valor de
la variable. La suma de las frecuencias absolutas es el total de encuestados.
Se denomina frecuencia relativa (se escribe fr) al cociente entre la frecuencia absoluta y el total
de etementos que forman la muestra. La suma de las frecuencias relativas siempre es 1.
Si a cada frecuencia relativa expresada en forma decimal se la multiplica por 100, se obtiene el
porcentaje de la variable.
)
rr=*
n es el número de elementos que formon la muestra.
EnÍrelos alumnos de primer año de una escuela sehomó una mueelra de diez alumnoe para
averiguar cuánlag materias tenían con calificación debaio de seie. Loe resullados fueron: O; O:
3:4:3:5:4:3:6;5.
)
guNA9,gsroy
ItA06lb hIAEUTSR
eoreUTlliEzt
¿Eg€ANR[O?AR?
)
)
1. Respondan y expliquen las respuestas.
a. iEs posible que la suma total de las frecuencias relativas sea 1,4?
b. ZQué significa que un valor de la variable en estudio tenga frecuencia absoluta igual a 3?
c. Si en un caso e[ porcentaje de un valor de la variable es27o/o, isignifica que la frecuencia
relativa correspondienle es 2,7?
d. iPuede suceder que para un valor de la variable el porcentaje sea
125o/o?
t |t
ifJlill3l1o,'utas y rerarivas
6.
Resuelvan.
Los chicos de 1.o año tuvieron que elegir eI nombre que los representará en una competencia intercolegial. Las opciones fueron nombres de pueblos originarios de la Argentina: toba (T), mapuche
(M), wichí (W) y diaguitas (D). De la votación se obtuvieron las siguientes respuestas.
M.M.M.W.W.W.M- D- D-T-M-T. D. M-M-M- D.M- M-W
W-D-D.M-W-M.W.M.T.D-M.M-W-W-W-W- D,T.T.W
a. Completen la tabla de frecuencias.
b. iQué nombre resultó ganador? ZCómo se dieron cuenta? ZQué porcentaje obtuvo?
c. iQué pueblos obtuvieron como máximo diez votos?
7.
Lean atentamente
y resuelvan.
El siguiente cartel muestra los horarios de las clases que se dictan en un gimnasio.
18-19
AEROBOX
SPINNING
PITATES
AEROBOX
AEROBOX
PII¡TES
t9-20
SPINNING
PII¡TES
¡lonenoór
PII.ATES
SPINNING
RITMOS
20-21
RITMOS
rlorencró¡¡
RITMOS
SPINNING
RITMOS
RITMOS
a. Completen la tabla de frecuencias.
b. iDe qué clase hay más horarios disponibles?
c. iQué clase tiene el menor porcentaje? iPor qué?
K"Jilj J J # #L*J
Gráficos
En muchas situaciones, los datos se pueden leer con mayor facilidad a través de gráficos. El tipo
de gráfico puede variar según la información que se quiere brindar.
Gráfico circular
Los gráficos circulares o de secciones sirven para mostrar la distribución de respuestas en rela-
ción con el total de resultados obtenidos.
9e realizó una encueeta ?aró conocer la opinión de 20 ?ereonde sobre un nuevo chocolale.
)
excelente 107o
regular 20%
Es un círculo dividido en sectores. Cada sector representa
una parte del total de los datos. El ángulo central de cada sector se puede obtener, por ejemplo, usando una regla de tres:
100%
malo
)
2Oo/"
10%
_
360'
1olñ3?o'
=zo
Corresponde
a excetente.
Gráfico de barras
-"=
Los gráficos de banas sirven para comparar la cantidad de datos que corresponden a cada valor
de la variable. Para confeccionar un gráfico de barras, en e[ eje horizontal se representan los distintos
valores de [a variable y en el vertical, las frecuencias absolutas. Luego, se construyen rectángulos del
mismo ancho cuya altura coincide con [a frecuencia absoluta del valor de la variable.
6
z
o
72
6
É
10
U
8
6
4
u
o
o
)
ó
o
F
7or ejemVlo, diezpersonas oVinan que eo
bueno.
2
z
Pictogramas
Los pictogramas son gráficos donde se representan cantidades a través de dibujos. Cada dibujo
representa una determinada cantidad.
1. Respondan y expliquen las respuestas.
a. iQué diferencías hay entre un gráfico circular y uno de barras? ZCómo muestra la información
cada uno?
b. En un gráfico circular, iqué ángulo central debe tener un sector que represenla el 25"/o del total?
I l+3
8.
AcnvrDADEs
Completen las oraciones teniendo en cuenta [a relación entre los porcentajes, la fracción del total
y e[ ángulo central del gráfico de torta.
a.
rrf-lz
se representa con [a mitad de un círculo y su ángulo central
.,
o.
l'.
., O" [-.l".
c et [-l'2" se representa con la octava parte de un círculo y su ángulo central ., O" [--.)".
U.
rf
a. rf
!z
se representa con [a cuarta parte de un círculo y su ángulo central
Ov.
se representa con la décima parte de un círculo y su ángulo centra[ es O.
9. pinten según corresponda.
a!ü
Luego, escriban el porcentaie.
b+
f]'"
[-l'.
{_;
!r"
c'ía
,, -..-.-.:-..
i\
\-*o"
i
./'
!r"
d.i'{+J/
,/
-_*\'
\
\/
!"
10. Representen en un gráfico circular. Pinten del mismo color cada sector y su referencia.
Mariana distribuye las actividades del día viernes de la siguiente manera.
iJ
f-l
a horas para dormir.
6 horas pasa en la escuela.
fi
fi
z horas para realizar la tarea.
z horas para jugar con sus amigas.
[J r hora y media para viajar.
fl t hora y media para navegar por internet.
il El resto lo utiliza en las distintas comidas.
\
1
I
11. Resuelvan.
Luego del estreno de una película se realizó una encuesta para conocer [a opinión de los espectadores. Las respuestas fueron las siguientes.
a.
ZDe qué
tipo de variable se trata?
¿A cuántas personas se encuestó?
b. Realicen el gráfico circular con los datos de la tabla.
l+l
AcnvrDADEs
12. Observen los gráficos y respondan.
Los gráficos muestran la cantidad de alumnos distribuidos por sexo en cada curso que hay en el
último año.
)
CURSO B
cuRso c
z
z
o
o
l
=
J
f
J
CURSO A
6
o
E
U
r
F
z
tr
I
U
o
ó
o
o
o
o
z
z
E
f
U
o
o
o
F
z
a. iCuántas mujeres hay en cada curso?
)
b. iEn qué curso hay menor diferencia entre la cantidad de varones y de mujeres?
c
Entre los tres cursos, icuántos varones hay? ZY en total cuántos alumnos hay?
13. Completen la tabla con los datos de sus compañeros de aula y realicen et gnáfico de barras
)
conespondiente.
14. Resuelvan.
a. Realicen el gráfico de barras de acuerdo con la información de la tabla.
b.
¿A cuántas personas se encuestó para obtener
la información anterior?
r l+l
t*:l?^"'
15. Observen los siguientes pictogramas y respondan.
o
El pictograma muestra la cantidad de libros que
É
@
hay en cada una de las salas de una biblioteca.
a. iEn qué sala hay mayor cantidad de libros?
4
o
o
o
ZCuántos hay?
tr
z
W@@-@
?re ?zs ?-.e
b. ZCuántos libros hay en total entre todas
?¿-
las bibliotecas?
(z¿e
Representa
looo libros.
16. Completen el gráfico y respondan.
La siguiente tabla muestra eltotal de habitantes
de la Argentina registrados en los últimos cinco
censos de problación.
a. iCuántos millones de habitantes creció la
población entre 1980 y 2O7O?
(e¡¡ ntr-t-o¡¡es)
f
*uor.r.n,u o ,,l,tlntlll*tts
Fuente: INDEC, Censo de Población y Vivienda.
17. Observen los siguientes pictogramas y respondan.
En el pictograma se observa la cantidad de"dÍas
que permanecen en el país los turistas que visi-
Cantidad de días que permanecen en la Argentina
tan la Argentina, según su lugar de procedencía.
a. A partir del pictograma, ise puede saber
desde dónde provienen los turistas que se
quedan la mayor cantidad de días?
b.
6e
puede saber la cantidad de gente
encuestada?
F¡}
Representa 5 días.
Fuente: INDEC, encuesta de turismo internacional 2010.
CONTENIDOS
,$*
l+¡.ql.qE.q3
ffi]$kl$
18. Resuelvan.
21. Observen y respondan.
En una editorial se realiza un control de calidad
Las tablas muestran eI deporte preferido en dos
analizando uno de cada 100 libros impresos. Se
los revisa y se decide si [a impresión final es
cursos distintos.
correcta o incorrecta.
a. El conjunto de libros utilizados para el
control de calidad, irepresenta la muestra
la población?
b. La variable estudiada Zes cualitativa o
o
cuantitativa?
19. tean [os siguientes datos y resuelvan.
)
En 30 comercios minoristas se averiguó el total
de paquetes vendidos de una marca de galtetitas. Los datos obtenidos fueron los siguientes.
6; 6; 4; 5;9;7; 6; B;3; 4; 5; 5;7; 4;9;
8; 8; 5; 6;9;8;9;8;7; 6;6; 6;7;5;3
a. iCuál es [a variable? Clasifrquenla.
b. Realicen [a tabla de frecuencias.
c. Representen en un gráfico la información
obtenida.
)
20.
Fútbot
a. iCuát es [a variable? iDe qué tipo es?
b. ZEn qué curso es menor el porcentaie que
prefiere natación? iY básquet?
Resuelvan.
La siguiente tabla muestra el estado civil de los
22.
empleados de una empresa.
Se analizó la frecuencia con la que los usuarios
Resuelvan.
de 50 automóviles cargan combustible durante
un mes.
a. Completen [a tabla con los datos fa]tantes.
)
a. ZQUé variables están en estudio?
Clasifíquenlas.
)
b. Realicen un gráfico circular donde figuren
los porcentaies según el sexo de los empleados de [a empresa.
c. Realicen un diagrama de barras que muestre el estado civil de los empleados.
b. iCuál es la variable? Clasifrquenlas.
c. iCuántos autos cargan aI menos cinco
d. ZQué porcentaje de las mujeres son casadas?
veces al mes?
d. iQué porcentaje carga como mínimo ocho
veces al mes?
23.
Observen el gráfico
y resuelvan.
E[ siguiente gráfico muestra
25. Observen el pictograma y resuelvan.
la cantidad de
I
o
É
publicaciones de viviendas (en venta) según [a
cantidad de ambientes, de una página de anuncios clasificados.
.a
o
u
6
o
o
F
z
¿
¿
.¿
.¿
I
.¿
I
I
.¿
.¿
es la variable? iDe qué tipo
b. Completen la siguiente tabla.
a.
ZCUáI
es?
CANTIDAD DE AMBIENTES
a. Realicen una tabla de frecuencias a partir
de la información del gráfico.
b. ZCuántos departamentos se publicaron en
total?
c. iQué porcentaje de los departamentos es
de tres ambientes?
d. iQué porcentaje de los departamentos
tiene como mínimo tres ambientes?
e. ZCuántos departamentos tienen como mínimo cuatro ambientes?
f. ZCuántos departamentos tienen como máximo dos ambientes?
24. tean atentamente y
resuelvan.
A un grupo de 24 personas se les preguntó qué
juego de mesa preferÍan. La mitad contestó las
cartas; la cuarta parte, el aiedrez; dos, el ludo y
el resto, las damas.
a. Completen la tabla.
c. Representen [a situación en un gráfico circular, indicando el porcentaje que le corresponde a cada uno.
d. Si cada páiaro del pictograma representa a
tres, Zcuántos pájaros tiene Juan?
e. Si entre todos tienen 72 pájaros, icuánto
representa un pájaro dibujado?
26. tengan en cuenta la infumación y resuelvan.
En [a siguiente tabla se registró por edad un
grupo de personas de un club.
Esteban
Matías
Juan
Carlos
Julieta
María
Ana
Graciela
Belén
Rocío
Rodrigo
Roberto
Mía
Micaela
José
Anabella
Daniel
Hernán
Silvana
Javier
Carolina
Pamela
Germán
Valeria
a. Realicen una tabla de frecuencias para
hombres y otra para mujeres.
b. La suma total de los porcentajes en las
b. iCuál es el porcentaje de los que prefieren
iugar al ajedrez? iY a las damas?
tablas anteriores Zes igual al
TOOo/d
Expliquen
la respuesta.
c. Realicen un gráfico circular para cada tabla.
Promedio, mediana
y
moda
W
Promedio
El promedio, también llamado media aritmética (se escribe x ), es el resultado de dividir la sumal
de todos los valores de [a variable por la cantidad de valores que forman la
muestra.
'
5e registraron las venlas diarias de gaseoeas de 600 ml en delerminado quiosco, duranle
una oemanay se o%uvieron los eiguienles
-
datos:20, 16, 17,22,20,26,25.
16+ 17 +20 +2O +23+25 +26 _ 16+ 17 +2.2O +2b
,/
+ 25+-?g
= 21
Moda
La moda (se escribe mo) es el valor de la variable que aparece más veces, es decir, [a que tiene
mayor frecuencia.
En el ejemVlo anterior,ffio=
20.
Mediana
La mediana (se escribe m") es el valor de la variable que está ubi-
cado en e[ lugar central luego de ordenar todos los datos de menor a
mayor. La mediana divide la muestra de tal forma que deja igual can-
tidad de datos a su izquierda que a su derecha.
Cuando la cantidad de datos es un número par, la mediana
es igual al promedio de los dos valores centrales.
0[eaiB[ENbiERl,l
?U'lÉb'
'b
t€UAltA Y ttluA?
EII[É,\\í
b\É
\€úAllA...
5i se ordenanlas cantidadee de qaseoeasvendidae,
se obtienelo eiguiente.
,i
1
6: 17 ;
20:Ñ
u- 23: 25: 2O
{/
'i
,t¡r:;r
mediano
1. Respondan y expliquen las respuestas.
a. Si la variable es cualitativa, ise pueden calcular las tres medidas anteriores?
b. La moda, ies el mayor valor que alcanza la variable?
c. ZCuál es la medida que divide los datos obtenidos en dos grupos?
d. EI promedio, isiempre es representativo de los datos?
toE
I l+l+
i:JJ,Yi3il:H.o*n,y
moda
27. Calculen el promedio, la mediana y la moda pan cada uno de los siguientes grupos de datos.
a. 36; 38; 40:, 40;38; 38; 38; 42;38;36; 42;36;36;38.
t:E
t:D
t:f--l
'.:D
'.:D
'"=f:-:]
'"=C::-l
'":-]
b. 28; 30; 28;28;28;28;29;35; Z9;30.
'"=[:]
c.32; 29; 42;34;34; 40;28.
d. 25; 40; 56; 74; 74; 72;
'=f:::l
28.
720:. 72:.
22; 44; 77;
'.:D
Calculen el promedio, la mediana
7OO;
16; 80; 77;32:'17;5.
'":
f:--]
y la moda.
Al lanzar un dado 30 veces los resultados que se obtuvieron fueron los siguientes.
'=
f:::]
r":
f---]
29. Completen los datos para que se verifiquen los resultados.
a.75;76; fZ; 16;
ffi.=16
ffio=16
b,15;76;f7;
m"
30.
[-l;
= 16,5
16;
ly¡o
=
[-l;
16
c.75;76;77;
ffi"
t6;C,
: 16,5 mo:
d. 15; 16;
ffi" =
C
77
77;76;CtC
15,5
mo
:
16
Resuelvan.
Juliana, Pablo y Ana han recibido las notas de sus dos primeras evaluaciones. Juliana obtuvo 7 y 6,
Pablo8y5yAna,9y6.
a. Si Juliana quiere tener un promedio de 8 y todavía debe rendir dos evaluaciones más, iqué
notas tendrÍa que obtener para alcanzar el promedio deseado?
b. A Pablo le falta rendir una sola evaluación, ipuede alcanzar un promedio de 9 con las notas
que ya tiene?
c
Si Ana rinde dos evaluaciones más y obtiene un promedio de 7, Zcuáles son las notas que obtuvo?
mnEEEanrt
Egedmentos aleatorios. Plobabilidad simple
Egedmenbs aleablios
Existen situaciones en donde no se puede anticipar cuál será el resultado. A este tipo de situaciones, que dependen del azar, se las llama uperimentos aleatorios.
Se denomina espacio mueshal al conjunto formado por todos los resultados posibles de un
experimento. Cada uno de los resultados que forman el espacio muestral se denomina suceso.
Experimento:f,irar un dado y obseruar el resulf,odo.
Eepacío muesiral:
1
,2,3,4,5,6.
Para determinar el espacio muestral de un experimento aleatorio, se pueden usar, por ejemplo,
diagramas de árbol y tablas.
En unabolsa se colocaronñchas con números
los 1,2,3.
)
deires cifras distrinlasformadoe porlos dígr
¿Cuál ee el espacio muestral?
A
El eeVacio
muestral esfáformado
Vor loe números: 123, 132, Zg1,
88 E8 8E
213,321,312.
Probabilidad simple
En matemática se asigna un número a la probabilidad de que ocurra un suceso. Ese número
puede ser 0, 1 o cualquier número comprendido entre el O y el 1.
Probabilidad de un suceso (P)
=
ffi
áetiraun dado:
,Todaslas caras de
un dadotienenlamismaprobabilidad de salir.
. Es más probable que salga un número
?ar que un divisor de 3.
. Es seguro que salga un número natural menor
que 7 .
. Es impoeible,
ejemplo, que ealga el número 10.
Vor
1. Respondan y expliquen las respuestas.
a. Elegir qué remera usar, ies un experimento aleatorio?
b. ZPuede el resultado de una probabilidad ser 3?
c. iEn qué caso la probabilidad es igual a
0?
r
1+5
ACTIVIDADES
Experimentos aleatorios. Probabilidad simple
31. Marquen con una X los sucesos gue son aleatorios.
a. El número que satdrá a[ tirar un Aado.
b. Próximo partido de un campeonr,o.
32.
(-.l
c. Que llueva dentro de dos afas.
fl
O
d. Ganar [a loterÍa.
Escriban el espacio muestral en cada caso.
a. Se tira un dado.
b. Se tiran dos dados y se suman los puntos.
c
Se lanzan dos monedas.
d. Se lanza una moneda dos veces.
33. tean atentamente y calculen [a probabilidad en cada caso.
En la ruleta, los números van del 0 al 36 inclusive (el cero está pintado de color verde y del resto
de los números, [a mitad son rojos y [a mitad, negros). Calculen ta probabilidad de que a[ arrojar
una bola resulte alguno de los siguientes casos.
fl
"'-"LJ
d. Un múttip," O" ,.
a. Un número par.l-
b. Un número de color
c
34.
Un número menor
,"¡..8
Or. ,r.
e. un número mayor
i
!
or"
oo.
[J
f. Un número menor o igual que 36.
[f
E
Respondan.
En la escuela están organizando un festival para recaudar fondos para una excursión. Los chicos
prepararon un puesto de tiro al blanco con dos discos y los siguientes premios.
DISCO A
a ZCon cuál de los dos discos se tiene más posibilidades
DISCO B
de ganar un oso de peluche?
b. En el disco A, Zcuál es la probabitidad de acertar en el color roio?
c
ZEn cuál
de los dos discos es mayor la probabilidad de acertar en el color verde?
.{
L*j
U
L**J L*-i
L.**i i L# t i t-*i
Cálculo combinatorio
El cálculo combinatorio permite conocer la cantidad de grupos que se pueden formar con determi-
nados elementos, de acuerdo con una serie de condiciones, sin necesidad de enumerarlos uno por uno.
?ablo, Guillermo, Verónica y Lidia com?rdron enlradas para ir al leaÍro y deben decidir cómo
ubicarse. ¿De cuánÍas manerds puedenhacerlo?
La
primem ubícación tiene 4 posibilldades; Ia sequnda poslcíón, 3; la tercera, 2, y ia cuarta,
4 . 3 . 2 . 'l = 24.Iienen 24 maneraa distintas de ubicarse
)
otro con mayor cantidad de elementos, también se puede utilizar el
disLinlas
pue
den hac erlo?
En este caso, la prímera ubicación sique teniendo 4 posibílidades y Ia
sequnda, 3. Y no quedan más luqares.
For Io tanto,
4 . 3 = 'l 2.
Tienen '12 maneras
distintas de decídir quié-
nes van y en qué aaientos se ubícan.
Hay casos donde se deben combinar elementos de distintos grupos.
Marcosva air al ciney debe elegir qué ro?d?onerse.No se decide
si llevar remera roja,blanca o neqra: si ponerse jedno negroo o azules y si llevar sus zaVatillas preferidae o los zapat os nuevos.
¿Cu
)
.
Si se quieren formar grupos con determínadas condiciones a partir de
cálculo combinatorio.
En el ejemplo anterior, si pierden doe enÍradas y deben decidir
quiénesvan alfeatroy cómo se ubican, ¿de cuáníae manerdg
)
1
en los asientos.
ántas
Tiene
Ni
en
2
jeans y 2 parea de zapatillas.
e p ar a
ve
bilsn}BnnusünkI
ot)uslEnRüb
uuilma. ¿E0¡[rfAg
nm\Eilumo?
wm,hnqE
Si
IATEI¡BETftN,
buouogn{ng.
sfir s e?
sibili d a d e s
3 poeibles remerae,
po
t¡B,tlt&fy.üIlD[16
Porlotanto,3.2.2=12.
Tiene '12 posibilidades distintas para vestirse.
)
1. Respondan y expliquen las respuestas.
a. ZQué ventaja tiene el cálculo combinatorio respecto de los diagramas de árbol?
b. Si además de saber cuántos números se pueden formar con distintas cifras, se quiere
saber cuáles son los números, 2qué estrategia de resolución se debe utilizar?
c. ZCuántos números de dos cifras distintas se pueden formar con los dígitos del 1 al 9?
r l+ E
ülJy,?13:?inatorio
Lean y resuelvan.
Laura está organizando sus vacaciones y tiene que elegir entre e[ campo, el mar o la montaña
como destino. Para viajar tiene que elegir entre auto, micro o tren y para alojarse, entre el hotel o
35.
la casa de una amiga.
a. iDe cuántas maneras distintas puede combinar las opciones para poder organizar sus vacaciones?
b. Si decide viajar en auto, icuántas opciones tiene para elegir?
c
Si su amiga no puede prestarle la casa, icuántas opciones tiene?
36.
Respondan.
Con los dígitos 2, 3, 5, 6 y 7 se desean formar números de tres cifras distintas.
a. iCuántos números se pueden formar? ZCUántos de ellos son pares?
b. ZCuántos son múltiplos de 5 y cuántos son mayores que 500?
37.
Resuelvan.
está
realizando una selección para poner en escena la obra "Romeo y Julieta". Se presentaron
Se
Z actores y 4 actr¡ces. iDe cuántas maneras pueden elegirse a los integrantes de la pareia protagónica?
38.
Respondan.
El papá de Matías, Daniela y Marilina quíere regalarles a sus hijos un libro a cada uno. Tiene para
elegir entre 3 libros de poesías, 4 novelas y 5 cuentos.
a. Si a cada uno le puede tocar un líbro cualquiera, ide cuántas maneras puede realizar la compra?
b. Si a Matías solo le gustan los libros de novelas, Zde cuántas maneras puede comprar?
c. Si quiere comprar un libro de cada clase, Zde cuántas maneras puede realizar la compra?
F
I
|
menteAcflvA
,ur.
de I
confeccionar un examen se dispone de 4 problemas de geometría, 3 de aritmética y 2
o"o.' aparecer en rorma consecu'li.
;::::.::f:,"f:::::;::i:;':il:l:,ii":',ffffii:l"
/
lnrEEHAElún
39.
43. Marquen con una X la opción
Respondan.
En la siguiente lista se muestra el peso de un
)
l+t+.¡+5.|+E
grupo de 12 amigos.
correcta.
Se lanzó un dado 50 veces, con los siguientes
resultados.
45 kg; 50 kg; 57kg;47 kg; sl kg; 60 kg;
55 kg; 53 kg;48 kg; 50 kg;46 kg; 50 kg
a. ZCuál es la variable? ZDe qué tipo es?
b. Calculen el promedio, la mediana y la
moda.
40.
a. iCuát es la frecuencia absoluta correspondiente a la cara 4?
16%
Resuelvan.
La siguiente tabla muestra [a edad de un grupo
de chicos que integran el equipo de fútbot.
a. Completen [a tabla.
to Ü
10%
Ü
b. ZCuál es el porcentaje correspondiente a
cara
Ü
r,6./"
f]l
rc./.
C
c. ZCuál es la probabilidad de que salga el
0,24
44.
b. ZCuántos chicos conforman el equipo de
fútbol?
c. Calculen eI promedio, la mediana y la
moda de las edades del equipo.
d. Realicen un pictograma que muestre la
situación presentada.
41. Calculen el promedio, la mediana y la
moda en cada caso.
a.3; 4;9;12:' 4;7; 8; 6;7; 4.
b. 8; 15; 7;9;70; 6;5; 5;3.
c 2;7;8;
42.
10; 10; 72:,
4;3.
Resuelvan.
[a
7?
0,16,%
)
[-l
n
,,oo
3?
24o/o
Respondan.
La siguiente tabla muestra [a cantidad de
amonestados que hubo en [a última fecha del
campeonato de fútbot.
a. Completen la tabla.
Racing
6
lndependiente
4
Boca
6
River
0
San Lorenzo
7
Vélez
2
Rosario Central
3
Dado e[ siguiente conjunto de datos.
4; 5; 6;7;8; 9; 8; 8; 9; 10; 12;
11; 10; 10; 11; 8;7; 5;9; 8; 8; 8
a. Calculen el promedio, la moda y [a mediana.
b. 5i a los datos anteriores se agrega el 654,
iqué ocurre con las medidas? iCambian?
Expliquen sus respuestas.
En determinadas situaciones, ison representativas todas las medidas estadísticas?
c
iPor qué?
28
b. ZCuál fue e[ porcentaje de amonestados
que tuvo Boca?
c iCuát es la frecuencia relativa de amonestados que tuvo San Lorenzo?
d. iCuántos amonestados tuvo lndependiente?
e. Realicen un gráfico de barras con las frecuencias absolutas.
45.
50.
Resuelvan.
Los siguientes valores corresponden a las precipitaciones registradas (en mm) mensualmente
en una ciudad del interior del país.
4A 36 24 43 56
78 78 44 78 4A
Respondan.
Con los dígitos
3,4y
2 se forman todos los núme-
ros de tres ciftas posibles para realizar un sorteo.
a. ZCuántos números conforman el espacio
78
muestral?
40
a
Calculen el promedio, la mediana y la moda.
b. Realicen un pictograma que muestre los
b. ZCuál es la probabilidad de que salga un
múltiplo de 4?
c iCuál es la probabilidad de que salga un
registros.
número impar?
Escriban tres experimentos aleatorios y
determinen sus espacios muestrales.
46.
47.
Resuelvan.
Se tiene un mazo de cartas españolas (50 car-
tas) y se toma una. Calculen la probabilidad en
cada uno de los siguientes casos.
a. Sea de oros.
b. No sea de espadas.
c
Sea imPar.
d. Sea un comodín.
e. Sea un número menor que siete.
f. Sea un múttiplo de tres.
51. Resuelvan los siguientes problemas.
a. Con las cifras 5, 6, 7 y 8, Zcuántos números de dos cifras distintas se pueden formar?
ZY de cuatro?
b. En una camioneta entran ocho personas. Si
todos saben manejar, ide cuántas formas se
pueden ubicar?
c
Una persona tiene cuatro remeras, tres
pantalones, dos camperas y tres pares de
zapatos. Si quiere vestirse con una prenda de
cada tipo, icuántas combinaciones distintas
puede realizar?
52.
48.
Resuelvan.
Una urna contíene siete bolillas rojas, cuatro
blancas y nueve negras. Calculen las siguientes
probabilidades al extraer una bolilla al azar.
a. Que sea roja.
b. Que sea blanca o negra.
c Que no sea negra.
d. Que sea de cualquier color.
Calculen la probabilidad en cada caso.
Antonella y sus dos hermanas compraron una
49.
docena de facturas: tres medialunas de grasa,
tres churros, cuatro medialunas de manteca y
dos vigilantes.
a. Si Antonella decide comer tres facturas,
ácuántas posibilidades tiene para combinar
las facturas?
b. Si eligen al azar una factura, icuál es la
probabilidad de comer un vigilante? ZY de
comer una medialuna de manteca? iY una de
grasa?
Resuelvan.
a. Para crear la bandera que represente al
colegio de Ana se deben utilizar los colores
rojo, verde, azul y amarillo. Si ta bandera
tiene que ser con rayas horizontales, ide
cuántas maneras diferentes se'pueden ubicar
los colores?
b. Eliana posee cuatro collares, cinco pulseras
y cuatro anillos. Si desea ponerse un accesorio de cada tipo, icuántas combinaciones distintas puede realizar?
c Nicolás tiene que rendir un examen oral en
el que debe explicar tres de los siete temas
gue se vieron durante el año. ZDe cuántas
maneras puede organizar su exposición?
d. En un restaurante el plato del día se
puede armar combinando cada una de las
siguientes opciones: una porción de carne o
una de pollo; como acompañamiento, se
puede elegir entre papas fritas, puré o ensa'
lada y como postre, helado, flan o ensalada
de frutas. iDe cuántas maneras se puede
armar el plato del día?
AuroEvALuAclón
I
I
53. Resuelvan.
En la siguiente tabla se observa la cantidad de materias que deben recuperar los alumnos de una
escuela en el mes de diciembre.
a. Completen la tabla.
)
b. iCuál es la variable? iEs cualitativa o cuantitativa?
c
Los datos obtenidos, icorresponden a la población o a una muestra? ipor qué?
d. Realicen en una hoja el gráfico de barras que muestra la situación.
e. Calculen el promedio, la mediana y la moda.
)
f. iCuál es el porcentaje de alumnos que tiene que recuperar entre una y tres materias inclusive?
54. Resuelvan.
tira dos veces un dado.
Se
a. Escriban todos los pares que se pueden obtener.
b. Calculen la probabilidad de que la suma sea 7.
55. Respondan.
En una escuela se deben cubrir los puestos de rector, director y vicedirector. Si hay diez candidatos, ide cuántas formas se pueden cubrir los cargos?
t-
h*
Srruroór lllcrAr
L
DC APnErDtzAlE
Observen la imagen y resuelvan.
e lnventen un enunciado con los datos que se necesitan para responder a las siguientes preguntas. Luego respóndanlas.
. Si se utilizaron 20 metros de soga, ca qué profundidad se encuentra el gancho?
. iCuántos metros de soga son necesarios para alcanzar el cofre desde el barco?
r ZCuántos metros debe descender aún e[ buzo para bnganchar el cofre?
b. Comparen el enunciado que inventaron con el de sus compañeros. iSon iguales? ZTienen las
mismas respuestas?
llúmeros negativos. Orden y representación
túmeros negativoc
Los números naturales también se denominan enteros positivos.
Los números negativos son aquellos que tienen adelante un signo menos. Estos números suelen
utilizarse, por ejemplo, para escribir las temperaturas bajo cero, indicar los subsuelos de un edificio,
las pérdidas de dinero, las fechas ocurridas antes del nacimiento de cristo, etc.
+3 =
-3 +
3 G fs un entero positivo.
Es un entero negativo.
Los enteros negativos, el cero y los enteros positivos forman el conjunto de los números enteros.
...-3,-2,-1 ,O,1,2,3.,
Orden
y
Los
puntos suspensivos indicon que existen infinitos negotivos y positivos.
representación
Para representar números enteros en [a recta numérica, pueden seguir estos pasos:
1. Se ubica e[ cero y se determina una distancia
entre dos enteros consecutivos.
2. Se representan los negativos a la izquierda
del cero y los positivos a la derecha.
-4-3-2-101234
A partir de la representación en [a recta, se puede decir que un número es mayor que otro que
se encuentra a su izquíerda.
'
-5
es mayor que -6.
tódulo o Yalor absoluto
Se llama módulo o valorabsoluto de un'número entero a la distancia que existe entre ese núme-
ro y el cero.
l-21= 2 5e lee nabr obsoluto de -2 es igual a 2'.
l2l= 2 Se be nabr obsoluto de 2 es iguol a 2'.
-3-210123
Dos números son opuestos cuando tienen el mismo valor absoluto y distinto signo.
2y -2 son opuestoe.
-(-2) = 2 Se lee 'el opuesto de -2 es iguol a 2".
f- Respondan y expliquen las respuestas.
a El cero ies positivo? 2Y negativo?
b. iEs cierto que e[ valor absoluto de un número entero siempre es positivo?
c Dos números distintos ipueden tener el mismo módulo?
il t+7
ffi:i3i?t-?-,*"-s.
clrri*n v represenracién
1. Indiquen el número entero que conesponde a cada situación.
a. Se realizá un descuento de $ZO en la primera compra con tarjeta de crédito.
b.Seacreditan$tsalsaldotelefónicoporunapromoción.
c.Laplayadeestacionamientoseencuentraene1tercersubsuelo.
d. Maria Angélica tiene una deuda de $:oo.
e.Ene1nordestedeFrancialatemperatural1egóalos15gradosbajocero.
f.Laempresadisminuyó[asventasenunpromediode50O0unidadespor'",.D
2.
Escriban una situación que represente el número entero indicado.
3.Completencon()o=.
a.-r!+
c.
u.-r!r-rr
d.
4.
-s
[-l Fst
r.-z!-+
[-l-z
e. r+t
-34[-l-usz
g.
l+31
C
h.l37l
o
l-31
-37
Representen en la recta numédca cada número y su opuesto con un mismo color.
-5; 4; -9; 6; -2; 8
01
5. Observen y resuelvan teniendo en cuenH que o, b y c representan números enteros.
a. lndiquen el signo de cada uno de los números que representan las letras y expliquen por qué.
b. Teniendo en cuenta el ítem anterior, iqué signos tendrán -a,
c. iCuát es e[ opuesto de b?
-b y -C
Í:
F
k
É
Adición
sustracción
Para resolver sumas y restas de números enteros, se deben tener en cuenta estos casos.
.
Si los números enteros tienen el mismo signo, se suman sus valores absolutos y el resultado
lleva el mismo signo que los sumandos.
En una ciudad, alae 7 de la mañana ee regielraron 3 grados bajo cero. Unahora después,la
temperaturabajó
-3 -
)
1=
-4
un grado.
¿CuálfuelaÍemperaturaregislrada alae B delamañana?
La temperatura fue de
-4
oC.
r
Si los números enteros tienen signos distintos, se restan sus valores absolutos y el resultado
[]eva el signo del sumando que tiene el mayor valor absoluto.
9i dos horae deepuée,latemVeralura eubió 5 grados, ¿a cuánto aumenÍó latemperaf,ura?
-4 + 5 = 1
La temperatum aumentó
a'l
oC.
Si en e[ cálculo aparecen paréntesis, se los debe eliminar aplicando estas reglas.
)
. Si e[ signo que lo precede
es "+", el signo del número
encerrado entre los paréntesis no cambia.
-15+(+12)=-15+12=-Z
-9+(fl--9-4=-13
.
Si e[ signo que lo precede €s "-", el signo del
número encerrado entre los paréntesis cambia.
)
]CND N
\íA IIABIANb \E ANffiES¡
\tE ]Htr$ CANgA\o, t'tgeR ttÉ
bt
AVERAbÑ\ERÉE.
3-(-2O)=3+20=23
5-(+16)=5-16=-11
1. Respondan y exptiquen las respuestas.
a. La suma de dos números negativos, ida como resultado un número negativo?
b. La suma de dos números enteros, uno positivo y e[ otro negativo, Zda como resultado
número negativo?
c iCómo se puede escribir una resta de números negativos como una suma?
d. iEs cierto que la suma de dos números opuestos es 1?
un
r l+E i:Il#1'nrrac*ér¡
6.
Resuelvan las siguientes sumas.
a.3 + (-4)
:
b. -2 + (-3)
D
D
:
c-5+G3):
o
o
d. -2 + (+9) :
e,3+(-¡):
n
f.3-(+5):
s. -2 - (-2) =
h. -3 - (-5) =
1.4 - (*3) :
i. -e - (-3) :
ü
D
c
D
C
7. Completen con el número que verifica la igualdad.
".Ü
+(2):7
",Ü+
b.-5+(-3)=C
8.
Lean atentamente
d.-3
+
e.4+(Ü) :-.
r.[+(+12):6
(+5) = 3
(Ü) =,
y respondan.
lazmín tiene una deuda bancaria de $¡OO. Si quiere saldar la deuda, Zcuánto dinero tiene que depositar? iCuál es la operación que representa esta situación?
y calculen cuál es el número.
a. La diferencia entre un número y -5 es igual a 2.
9.
Escriban en lenguaje simbólico
b. La diferencia entre un número y
c
La diferencia entre un número
-9
es igual a 10.
y 3 es igual a 0.
10. Completen la tabla.
menteACT|VA
En la calculadora de Malena no funciona el signo
mente la suma 340 + 520.
a. iQué operación pueden hacer?
b. áCuát es el resultado?
"+'y
necesita verificar si resolvió conecta-
Multiplicación y división
Para multiplicar o dividir números enteros, se deben tener en cuenta estos casos.
. El producto entre dos números de igual
.
signo es un número positivo.
tinto signo es un número negat¡vo.
4.2=2+2+2+2=B
El producto entre dos números de dis-
4.(-2)=-2-2-2-2=-B
(-4) 2=-4-4=-B
-(-3)=(-1).(-3)=3
\t
\-/
.
.
Si se dividen dos números de igual
signo, el resultado es positivo.
Si se dividen dos números de distinto
signo, el resultado es negativo.
1O:5=2?orque2.5=1O
10 : (-5) = -2 ?orque (-Z) . (-5) = 10
(-1O):5 = -2 ?orque (-Z) .5 = -1O
(-1O) : (-5) = 2 porque 2 . (-5) = -1O
Para saber elsigno de una dívísión o muttipticación de
números enteros,se puede utí[izar la regta de los signos.
. Sí los sígnos de los dos números son iguates,e[ resuttado
es positivo.
+.+=+
.
-,-=+
+',+=+
-',-=4
IA CCAAVAETIAL
Si los signos de los dos números son distíntos,e[ resutta-
do es negatívo.
+ -=-
El
- 1=-
+,-=-
(-86fl : 216
de 864 . 216 y de (-86fl : (-216)
resultado de 864 . (-216) y de
El resultado
-'+=-
Crslbtül[Ulft¡$
bEl¡0lf6Nffifi\hA
tg il'ruSE qnfcÉA-:
es negativo.
ee Vosifivo.
1. Respondan y expliquen las respuestas.
a. iEs cierto que (-3) . (-S) es igual a 6?
b. El producto de un número positivo por un número negativo
Zes un número positivo?
c. El cociente de dos números negativos Zes un número positivo?
d. ila regla de los signos para el producto es la misma que para e[ cociente?
e. aA qué es igual el cociente entre un número y su opuesto?
t t+ t
t-T,llJilffi',, y divisién
11. Resuelvan las siguientes mulüplicaciones.
a.3.(-2):O
b.7 .0: O
c.
(-rz).eA:
d.-2
.3:
s.-2 .3 . F2):
h.-3. (-2).(-1) = O
C
e.725.(-2).0:
f.-2.(-5).eo):D
C
i.-2.e4).to:
o
12. Completen la tabla.
-2
3
-3
5
0
7
-1
-4
4
-2
13. Resuelvan las siguientes divisiones.
a.72; F¿ =
b. -18
c. -34, (-2) :
C
d.-725 :25
: (-3) :
O
=
e. -60 ,
rz =
f. -1oo , (-2)
[-l
:
O
14. Completen con el número entero que f'alta para que se cumplan las siguientes igualdades.
o.n.(-5):1oo
c.
-7
.l-l
:
-270
o.E.e3):t+z
e. 15.D:-ou
f---] : -ru
n.f_J:(-6)=o
s. -725,
t'D:(43):1
15. Lean atentamente y respondan.
Romina le pidió a su papá $600 prestados.
a. ZCuál es el número entero que representa la deuda que tiene Romina con su padre?
b. Si en el mes de septiembre le devuelve un tercio del dinero, Zcuá[ es la operación que debe
realizar para calcular cuánto [e tiene que dar a su papá?
c. ZCuál es el número que representa la cantidad que aún le falta pagar?
menteACT|VA
iQué signo üene el resultado de cada cálculo?
a. (-5) . (-15) . e25) . (-45): (-s) : (-1s) . (-115) . (-115) : (-5)
b. (-8) . (-8) . (-64) : (-8) . (-4) . (-128) : (-16) : (-1)
c (-240) . (-344) . o . (-441) : (-3) . 504 : (4) . (-115) : (-80)
I
t
l
iE
¡r
ttf¡ti¡¡*á¡ttiÍ¡*b
L
re
=.
j F*¿*{ii t,*,,*,,i, L**&gl¡i t"*édj¡rL*"*#¡;L.-**,:;j;l L, _ *j
¡
Operaciones com binadas
Para resolver un cálculo combinando las cuatro operaciones con números enteros, se deben
seguir los mismos pasos que con los números naturales.
-42.o:4+4+s q-$-ffr=
-252 : 4 + 4 + (-1 5) - (-16)
1. Se separa en términos.
2. Se resuelven las multiplicaciones y divisiones,
aplicando la regla de los signos. I
=
-63+4+(-15)-(-16)=
-63+4-15+16=
3. Se suprimen los paréntesis.
4. se resuelven las sumas y
restas. ;l.T#flüjll
@+16)-(63+15)=
20-78=-58
rEla
de los
siqnos.
Para resolver un cálculo combinado donde hay paréntesis, primero se separa en términos. Luego
resuelven las operaciones que ellos encierran.
(-17 - 41) . (-2) + e6: (-32) - 1oo
(-58) .(-2) + e6: (-32) - 1oo =
116 + (-3)- 1OO =
=
1. Se separa en términos y se resuelven las
operaciones que se encuentran entre paréntesis.
2. Se resuelven las multiplicaciones y divisiones.
3. Se suprimen los paréntesis.
116-3-1OO=
116 - (3 + 1oo) =
116-1O3=13
4. Se resuelven las sumas y restas.
PRiUEbTA¡€p qf, o&RAR A UN
lAe€lüE lÉ ArErüuctrgr \EsrÉg A 0rrA
t6mE,
cñiAR¡rTAg,Y TIASTARE A
ofBosÉr*,\É rA ftritrA.
eSrg qf
qt Sol¡
otÉRA[hf6 o,tsllA\4$.-
1. Respondan y expliquen las respuestas.
a. ZEs cierto que -1 + 1 . 2 : 0?
b. En un cálculo combinado, ise pueden resolver primero las sumas y las restas y luego las
multiplicaciones y divisiones?
c. iQué significa el signo menos delante de un paréntesis?
I 5 n ff-'Iitf-t-?combinadas
16. Unan con una flecha cada cálculo con su resultado.
a.3-5.(-z)+s:
b. -23 . (-2) * 23 -
o -25
72: (-6) :
c 45 - 45 : (-9) + 8 - 7 . (-3) =
d. 79 : (-rq) + 15 . 0 - 18 . 3 :
e. 15 + 16 : (-4) + 12 . (-3) :
.77
.
2'J.
17. Observen cómo resolvieron Martín y Laura los cálculos y respondan.
Martín
2-5.(-2)+4:
4.(-2)+4
6+4=ro
st
o
0
r
i3
'rf
¡t
@
Laura
2-5.(-Z)+t+:
2-7O+4
-8+4:4
iResolvieron correctamente los cálculos? ZPor qué?
18. Resuelvan los siguientes cálculos combinados.
a.-'J,. (-3) + 6 : (2-tS z3) + 4:
b. 18
: 02 - 3 . 2) + 2 . (26 -
72 . 3)
c24-672: (-36-5.12) -15
:
d. Ot +16) . (-1) - (23
=
- 6) . 3 =
19. Coloquen los paréntesis donde conesponda para que se verifiguen los resultados.
a.72-3
b,72-3
c.12-3
20.
4-5
4-5
4-5
-55
.
.79
2:26
2:-10
2:-2
d.12-3
e.72-3
f.72-3
4-5
4-5
4-5
Rodeen el resultado conecto en cada caso.
a. El triple de la diferencia entre cinco y doce.
-27
2t
b. El doble del opuesto de tres más cuatro.
t-142
c. La tercera parte de la suma del opuesto de ocho y el módulo de
1-3-1
5.
2=-54
2:7O
2:18
lnrEEHnnmn
2f.
l+7-19-l'l9.5n
Ubiquen en una recta numérica los siguien-
tes números.
a. -5; -:L;2; -2; -6;8
b. -'L; -3;0; -10; 72; -72
22.
Escriban un nfimero que represente cada
situación.
a. La temperatura-fue de 3 grados bajo cero.
b. La deuda bancaria es de $500.
c Una fosa marina es de 8800 m.
d. Tengo $zoo.
e. Debo $zoo.
f. Un bebé bajó 300 g en su último control.
23. Lean atentamente y respondan.
¿ ZQué número es mayor: -3 o elopuesto de 8?
b. iQué número es mayor: el módulo de -5 o 5?
c iQué número es menor: -4 o el opuesto de 5?
d. iQué número es menor: el opuesto de 3 o
el opuesto del módulo de -3?
24. Completen con el anterior y el posterior
cada número.
a.
b.
c.
d.
.€.
t
t-l
t-l
,-r,f---]
(
r-l
-500,
( t-3t (
[-l
f-l
(-(-31),f:.']
25. tean atentamente y
respondan.
a. iCuántos números naturales se encuentran
entre
-6 y -3?
b. ZCuántos números enteros se encuentran
entre
26.
-6 y -3?
Completen con
a.-r!-r
u.o!-z
c -a
fl
a. ro
f-l -zo
rst
(¡ ) o =.
[-l-rs
t.-+Q-z
s. atilQlrz
rr. + ['-l r-zr
e.
-rz
28.
Resuelvan las siguientes sumas
d. -3 + (-5) =
b. -4 + (+8) =
r-e-(-3):
d.0-(+3):
e --72 -
y restas.
G2)
:
f. -79 - (+19) =
s. -7e - (-1e)
:
h. 20 - (+24) =
Lean atentamente y respondan.
a. Si a pertenece a los números enteros, iqué
29.
número hay que sumarle para que dé como
resultado cero?
b. Si b pertenece a los números enteros, iqué
número hay que restarle para que dé como
resultado cero?
c Si c es un número entero negativo, isu
opuesto es un número negativo?
de
,-o,f.-]
f-l
f-l
27. Orde¡en de menor a mayor.
a- -{20i;r,4; -36; l-zl;-lr37; o
b. -40; -l-t+l; SZ; -3; 4;723;7
c.15; 44;0; -2;33;740; -72;3
30,
Lean atentamente
y resuelvan.
a. Un famoso matemát¡co nació en el año
384 antes de Cristo y murió en el año 322
antes de Cristo. iCuántos años vivió?
b. Algunos documentos afirman que Thales de
Mileto nació en el año 624 a. C. y hlleció en
el año 547 a. C. iCuántos años vivió?
c Si una persona nació en el año 15 a. C. y
murió en el año 43 d. C., Zcuántos años vivió?
31. Resuelvan los siguientes problemas.
a En una montaña donde se practica esguí,
la temperatura más alta fue de -3 oC, y la
más baja, de -25 oC. ZCuál fue la diferencia
de temperatura?
b. Un avión vuela a 9000 m y un submarino
está a -850 m. iCuál es la distancia entre
ambos?
c
Cecilia tiene $250 en el banco y debe pagar
$fSO ¿e lnternet y $180 de expensas. ile
alcanza el dinero? iCuánto le falta, si ademáÉ
quiere pagar $tZO de la cuota del gimnasio?
32.
38.
Resuelvan.
Hernán se retrasó varios meses con el pago del
servicio de televisión por cable y financió su
deuda de $zeo en 6 pagos.
a. Si abonó $520, ¿cuántas cuotas pagó?
iCuál es el valor de cada cuota?
iCuánto dinero [e falta pagar? iQué opera-
b.
ción debe realizar para averiguarlo?
33.
Respondan.
a. ZCuál es el triple de -3?
b. iCuál es el número que al dividirto por -2
dé como resultado 5?
c ZHay algún número que al dividirlo por -7
Completen
y respondan.
a. ZCuáles pueden ser los factores para que
se verifique e[ siguiente producto?
C O=,,
b. iExiste una única posibitidad? En caso de
existir otra, indiquen cuál.
c ZPueden ser los dos factores positivos?
iPor qué?
35.
Resuelvan las siguientes divisiones.
a. -15 : G3)
:
il. t4 : (-7) =
¿.24 . (-t)
b. 1o : (-2) =
G -18 : (-3) :
:
f.t6:o:
(, ) s =
sin hacer lq cuen'
ta. Expliquen cómo lo pensaron.
36.
Completen con
a.2 . (+l
!e
b.-4.(-r)!rz
c.-4:{-zl!-z
d.18:{-r)!z
37.
Resuelnan los siguientes cálculos combinados.
a.2.(-3)+5-15:(-3):
y respondan.
Julia introdujo el siguiente cálculo en la calculadora: 3 - 5 . 2 + 4 y obtuvo 0 como resultado.
ZEs
correcto? iPor qué?
39.
Resuelvan.
-
- 72. (-3) =
b. -(23 - 36) .(-3) - 34 , (-2) :
c. 48 - 3 . 29 - (3 - 23 . 4) - 24 : (-24) :
d.-53-(4.2+18)-20=
e.-30-72.2-Ge-4.2)=
l. 25 - (-t . ++ 5 . 8) - 3 . (-7) :
a. 2
40.
-
O2
45) + 3
Escriban en lenguaje simbólico
y resuelvan.
disminuido en
dé como resultado cero?
34.
Observen atentamente
b. tz + 3 : (-3) - 76 - 4 z F2) :
G -3 . 6 . e7) - 60 + t2: (-6):
d. 34 . (-$) + 72: (-3) - 4 . e, :
e.23 - 25 . (-5) + 725 - 72 =
a. El doble del móduto de -8
4 unidades, aa qué es igual?
b. La mitad de la suma entre el opuesto de 8
y 20, ia qué es igual?
c E[ producto entre el opuesto de 4 y un
número es igual a -72. LCUáI es ese número?
d. El cociente entre un número y et módulo
de -5 es igual a -6. iCuát es ese número?
e. La diferencia entre e[ siguiente de -3 y el
opuesto de un número da por resultado -5.
iCuá[ es ese número?
La suma entre e[ opuesto de 4 y un número es igual a 14. ZCuá[ es ese número?
f.
41. Resuelvan los siguienbs cálculos combinados.
a. -22 : (-rr) - (-18 + 14 : 2) + (-7) :
b. z + 8' (-a) - 14 + (a2) : 4l :
c. (-24), (-6) - [8 : (-4) - (-2 - 3)1. z + t :
d.(-3) +3.(-4 + 5) - 5.1-2+7 .(t) + 9l =
e. (-1 - 8) : (-3) + ( e - 2 . 5) . (-2) . (-2) =
f. -(-+ + 5) + 3 - 27 : (-7) : 3 . (-19 + 22) :
42.
Respondan.
a. iEl triple de[ opuesto de qué número
sumado cinco da como resultado L4?
b. iEt doble del siguiente de qué número da
como resultado -10?
ZLa tercera parte de qué número es -30?
d. ila suma entre qué dos números enteros
c.
es -15?
e. 2La diferencia entre qué dos números enteros
es -L0?
AuroEvALuAclór
43.
a
4Il.
Escriban un número que represente cada situación.
segundo subsueto.
f-l
Ordenen de menor a mayor
b. Debo sloo.
f-l
c
euinto piro.
[-l
y representen en la recta numérica.
-18; l-211; 6; -75;9
45. Completen la tabla.
46.
Resuelvan las siguientes operaciones.
a.15+(-3)=
c -9 -
b. -12 +
d.76 . (-2) =
47.ltnan
(+8)
(+72)
e.
J.-75: (-5)
cada cálculo con su resultado.
o _I7
o74
.79
o -22
o -32
o24
a.3.(-2)+5.4=
b.-z+3.(-4)+7:
c.72:(-2)+a.(-s)+6:
ll. -4 - 76 : C4) - 72 + 5 . (-z) =
e.72 + (-z) . t+ - 10 . (-2) :
f.75-(-r0):(-8)+3.2=
4&
)
18:e9)=O
o -l¡
o-/
Resuelvan las siguientes operaciones combinadas.
a.3.(-2+5)-(4-5.2):
c--72-(3.
b.7-(2-4)+6:
¿ -(-3 + 4 . 2). 5 -
2
-
8) +
72 (-6):
(s . 2 + 3) =
=n
FECTTA
crpfrulo I
Números naturates
c Plrulo t
Fracciones y expresiones
decimales
c/¡¡rfrure J
Funciones
cepfrulo
l+
Cuerpos
c*pkulo
S
Ángutos
cAPíruLo E
Figuras planas
cnpfrulo
7
Perímetro, área y volumen
crpín¡ro
E
Probabilidad y estadística
crpÍn¡ro t
Números enteros
EE
EITREü
cff.rncActór
Números naturales
En un juego de mesa, hay cartas con descomposiciones de distintos números. Cada jugador recibe
una tarjeta con un número y debe [evantar cartas deI mazo hasta juntar las tres descomposiciones
que corresponden a su número. Gana e[ que logra juntar primero las tres descomposiciones.
Lota jugó con Flor y con Marcos. Estos son los números que les tocaron a los chicos.
-"--"f
g
LoLA
X
L:JUrcAe"*L
+oo+o
--
o
1
44oo5
I
t
I
4
¡-"
a. Flor dice que ganó. Estas son las cartas que juntó. iTiene raz6n? ZPor qué?
4OOOOO+4OOO+B
4.105+4.103+B.1Oo
t
4.1OOOOO+4'1OOO+B
,-:_.¡
b. iQué cartas debía juntar Lola para ganar? ZY Marcos?
2. Descompongan los siguientes números en potencias de diez y respondan.
45650
:
54506:
a. Si las cifras de los números anteriores son las mismas, Zpor qué los números no lo son?
b. ZQué posicíón ocupa la cifra 6 en cada número? iRepresentan el mismo valor? iPor qué?
)' -
3. Rodeen con color el número que cumple con las condiciones indicadas.
y menor que 123. Todas sus cifras son diferentes. La cifra de las unidades es la
Es mayor que372
mitad de la de las centenas. La diferencia entre las centenas y las decenas es
1472
1
540
7545
1653
100.
4.
Resuelvan e indiquen las operaciones que tienen el mismo resultado.
a.
lro60.z'-.,[9oo z3=
b.
(103)'?
:
(103
. tG)
+ 1[64 =
c
(5. . 5 . 59 : (57)' +-,tB
d.
'tr6E
+ \86-
. 't]rÉ
:
-./9 - G .2)o =
5. Escriban lo pedido en cada caso.
a. Todos los divisores de 36:
b. Los primeros seis múltiplos de
13:
G E[ mcm (78;24;30)z
d. El dcm (78;24;30):
e. E[ mcm (48;56;84):
f. el dcm (48;56;84)z
6.
Unan con flechas la expresión simbólica que corresponda con cada enunciado.
.2. (a + 1) + 10
a. E[ doble del tripte del anterior de un número.
. 2 . 3 . (a - 1)
b. Et dobte del anterior del triple de un número.
o 2 . (3a - 1)
c El siguiente del doble de un número aumentado en 10.
o (2a + 10) + 1
d. La suma entre 10 y el doble del siguierite de un número.
7.
Resuelvan las siguientes ecuaciones.
,., . (t+ 4x) :
2x +.,[87 .
b. 3x + 16 + 5x - (2 . 5 + 1)
c 3 . (x2 + 50) +
lÍ:l . 2 + 6 . 3
^l@ =
2z
:
6x + (72 - 8)
d..,/x-úoo:2=42-4.2
Fracciones
y expresiones decimales
1. Marquen con una X las figuras en donde se pintó
".o
o.
f.
o.!
..o
fl
2. lndiquen la fracción que representa cada letra.
Luego, escriban la expresión decimal que
corresponde en cada caso.
0
E t-r
:
ct-
b=
3.
b1
E
:
r-r
2d
c
E =f-:l
L-
d=
E
=
e3f
e=
E
f:
E
c-]
:
f-r
=
t-l
Exoresen como fracción irreducible.
''#=E '#:E
4. Marquen con
una
X las fracciones decimales.
-99
r"
l ooo
b.#
a.$
''s:B ''ás=E
''#:E
".+c
5. Ordenen de menor a mayor.
#rt,
6.
o,2;?;0,301; 0,3;
l; o2
Escriban [a expresión decimal que corresponde a cada fracción.
lf; :
b.+ =
a.
f-l
f-l
"3=f-l
d.+=f-l
".#
f.3:
=
t-l
[-l
7. Completen con (, ) o =, según corresponda.
..
f [-l
b.33
o,zr
C r,t
" lf
[-l o,oo+
u.!!r,6
[-l o,ttt
t,t,rQ33
e. o,57
8.
Escriban como fracción ineducible.
¿o,ee:E b.o,e=B co,oe=B d.o,27=B
9.
Escriban en lenguaje simbólico
a. La diferencia entre la
e.0,72:E
y resuelvan.
raíz cúbica ae
{
V e[ cuadrado de 7,2.
b. El cociente entre el cubo de 0,2 y la raízcuadrada de la diferencia entre 1 y E.
c. La suma entre e[ cuadrado de ta mitad de
d. El producto entre la raíz cuarta
Oe
f
V 0,39.
fr V la raíz quinta de $.
10. Resuelvan las siguientes operaciones combinadas.
,S-t8.4 ,E:
b.(3)'- (+)',.
1L
# +:
c- 0,22.
T .r iF - 0,6 =
d.0,52:|+2,5-ffi:
Resuelvan las siguientes situaciones problemáticas.
a. De un rollo de cinta de 25 m, se deben cortar 1,2 m para la confección de moños. iCuántos
moños se pueden obtener? ZQué porcentaje de la cinta sobra?
b. En un libro de Matemática se destina el 65"/" de las páginas para eiercicios, el 25% del total
para la teoria y el resto para los trabajos prácticos. Si tiene 24 páginas de trabajos prácticos,
Zcuántas páginas tiene el libro? iY las demás secciones?
Funciones
1. Resuelvan.
a
Escriban las coordenadas de cada punto.
a-
b=
L-
d=
e:
f:
0
)
b. Representen los siguientes puntos
en un sistema de ejes cartesianos.
:
b:
a
s
(ZOO;/+)
(400;6)
=
(50;2)
d : (o;8)
e : (250;10)
f : (450;72)
2. Resuelvan.
E[ siguiente gráfico muestra
a
la cantidad de casas vendidas durante un año.
ZCuántas casas se vendieron en
el mes de
mano?
t4
b. iEn qué meses se vendieron más
casas?
o
/
o
F
c. jEn qué mes se vendieron 180 casas?
iY menos de
d.
L,
/
7707
ZEn algún mes
no se vendieron
\
casas?
e. iCuántas casas se vendieron entre abril y
\
I
\
I
/
0
:s
julio inclusive?
.L
!o
3. Completen las tablas para que se cumpla lo indicado en cada caso. Escriban la constante de
proporcionalidad.
a. Variables directamente proporcionales.
b. Variables inversamente proporcionales.
42
5
14
21
10
o:
35
f__:l
o:
[-l
4. Escriban un ejemplo de proporcionalidad directa, uno de relación de proporcionalidad inversa y
otro de relación no proporcional.
5. Resuelvan.
Malena quiere ampliar una foto de su perra para colocarla en un portarretrato, sin que se deforme.
Las medidas reales de [a imagen son de 10 cm de ancho por 15 cm de alto.
a. Si el ancho de la foto debe ser de 30 cm, Zcuánto debe medir el alto?
b. Si el alto de la foto pasa a ser de 30 cm, Zcuánto debe medir de ancho?
c
La relación entre el ancho y el alto de la foto, Zes directa o inversamente proporcional? iCuál
es la constante de proporcionalidad?
6.
Lean atentamente
y respondan.
Guadalupe recorrió, con su bicicleta, cierta distancia en 2 horas con una velocidad de 20 km/h.
a. Si quiere reducir la velocidad a [a mitad, Zcuánto tiempo tardará?
b. Si quiere recorrer la misma distancia en una hora, ia qué velocidad debe
ir?
c. ZLas variables son directa o inversamente proporcionales? ZCuál es [a constante de proporcionalidad?
Cuerpos
1. Completen con el cuerpo que corresponde a cada objeto.
a. Rollo de servilletas.
e. Pelota de tenis.
b. Caja de zapatos.
f. Tanque de agua.
c. Dado.
g. Ladritlo.
d. Bonete.
h. Lata de pintura.
2.
Escriban
V (Verdadero) o F (fabo). Expliquen las respuestas.
a. En cualquier pirámide, [a cantidad de caras coincide con [a cantidad de vértic.r.
O
b. Un prisma de diez caras tiene diez vértices.
c
Un cilindro no tiene .urur.
[-]
d. La cantidad de aristas de la base de cualquier pirámide es igual a la cantidad de vértices
menos
1
O
3. Marquen con una X cuál de tos desarrollos corresponde a un prisma de base hexagonal.
ab.c.
4.
Copien el siguiente desarrollo y construyan el cuerpo. Luego, rodeen con color el cuerpo que
corresponde al desarrollo.
5. Unan con flechas la cantidad de caras con el nombre del poliedro regular conespondiente.
a.72
r
b.s
o Octaedro
c4
o lcosaedro
d.
o Tetraedro
15
.
e.20
Cubo
Dodecaedro
Í.6
6. Representen la siguiente situación y luego, completen con ll(Paralelas) o I (perpendiculares).
^ll4cLAyBllo
rO.
7. Completen
con
.Co
oCo
ll(paralelas), -|. (perpendiculares), -¿i (oblicuas) o AL (alabeadas).
B
D
Calculen lo pedido en cada caso teniendo en cuenta los ángulos dados.
a(d*0)'t=
fi = xF ut, f; = TT 2T; i = n&B: 30'
c'i-(&.01:
d.ff'r*f:
b.iz2-&:
)
)
)
2- Coloquen una X para indicar la relación que existe entre & y f,.
3"
Escriban las ecuaciones
y resuelvan.
a
El
b.
La tercera parte de un ángulo es de 15o 20'. iCuánto mide el ángulo?
triple de un ángulo es 1650 30'. iCuánto mide el ángulo?
e. La suma entre el doble de un ángulo y su suplemento es 200o. iCuánto mide el ángulo?
4.
Calculen el valor de los ángulos desconocidos
Datos:
PAQ
&":
)
22o 35'
l-l
¡.8*&= [-l
a€-c[':
.A*d*é:f-l
y
resuelvan.
t-l
6- l-l
¿B=
f-l
¿6.4-a:r-l
e.tA-6).r=t---l
Í"&"22*t=
f--]'
5.
Resuelvan.
a
Dibujen un ángulo obtuso y divídanlo
en cuatro ángulos iguales.
6.
Tracen lo pedido en cada caso
b. Dibujen un ángulo cóncavo y tracen
su bisectriz.
y completen.
a Tracen
[a mediatriz de mq y llamen f al punto medio.
b. Tracen las mediatrices del n¡t y det tq. Llamen r at
punto medio de nrt y z al punto medio de tq.
c Escriban V (Verdadero) o F (Falso) según corresponda.
. nrr mide lo mismo que tz.
. nrr mide lo mismo que tq.O
. f es punto medio delE. O
7.
Planteen la ecuación y calculen el valor de cada uno de los ángulos de las figuras.
a
Datos:
MIT
a=7x
F:4x+18o
t=5x+80
&=O
6:C t:O
&=O
0:O A:O t:O
b. Datos:
ft,:4x+72"
&. = 6x- 24o
F:2x-too
Figuras planas
1. Lean atentamente y resuelvan.
Una artesana quiere armar portarretratos de forma triangular. Para ello, cuenta con dos maderas de
8 cm, dos de 5 cm, cuatro de 9 cm, dos de 72 cm, dos de 15 cm y tres de 3 cm.
a. Completen la tabla con algunas de las posibles combinaciones que puede armar según la longitud de las maderas. Tengan en cuenta la cantidad que tiene de cada una.
)
b. ZPuede armar portarretratos con todas las maderas? ZPor qué?
c
)
Clasifiquen los triángulos que forman los portarretratos según sus lados y sus ángulos.
2. Resuelvan.
a Calculen la medida del lado desconocido
FIGURA A
)
-:[-l
sabiendo que e[ perímetro total de cada potígono es 35 cm.
FIGURA B
FIGURA C
n:[-l
':f_:J
b. Calculen [a suma de los ángulos interiores (SAl) de cada uno de los siguientes polígonos.
3.
Calculen la medida de los ángulos desconocidos.
a.
En el trapecio isósceles defg,
el 0 mide
et cuádruple Aet
á y el é mide
36o.
b. En et pentágono irregular stuvw, et t mide ta mitad del A. rf ü mide 3Zo más que et t. rt
mide 47o más que et A. ¡t fi mide 10 más que el tytmider3o".
V
4.
Tracen en las siguientes circunferencias lo pedido en cada caso.
c. Un diámetro pq
Una cuerda ab de menos de 3 cm y
otra
a
cuerda cd de 3 cm.
b. Una cuerda
ft
a
de más de 1,5 cm y uno de
y una cuerda E perpendicular
[!, de menos de 2,5 cm de longitud.
d. Un sector circular con un ángulo de
80o.
los arcos que quedan determinados.
5. Completen la tabla.
lrregular
3
360"
Regular
Trapecio isósceles
lrregular
4
Regular
600
Regular
Regular
6.
1
0800
400
Construyan en sus carpetas las siituientes figuras.
a. Un triángulo isósceles cuyos lado$;iguales midan 5 cm y el lado desigual mida 3,5 cm.
b. Un paralelogramo cuyos lados midan 2,5 cm y 4,7 cm y uno de sus ángulos mida 45o.
c Un pentágono regular de 4 cm de lado.
Perlmetro, área y volumen
1. Ordenen de mayor a menor.
a,7 500 dm; 48 m; 5 600 mm; 0,5 km; 50,4 dam
b.3,2 dam2;500000
mm2; 0,052 hm2; 800 dm2
c. 0,65 m3; 0,0012 dam3; 420000 cm3: 3000 dm3
d.3500 l;4 kl;9800 dl;12
hl
)
2. calculen el área lateral, el
área total
a. Cilindro.
Área lateral:
12
cm
Área total:
)
Volumen:
y el volumen de los siguientes cuerpos.
b. Pirámide de base cuadrada.
f-l
Área lateral:
f-l
f-]
t-l
Volumen: f-l
6 cm
Área total:
(-l
5cm
3. Completen la tabla sabiendo que se hata de pdsmas de base regular.
4.
Cuadrada
1cm
Pentagonal
2dm
Hexagonal
3m
Octogonal
3mm
2cm
3dm
3m
cm3
27
m3
24 ml
15 dm2
1m
10 mm
24
320
mm2
476 mm2
480
mm3
0,48 ml
Resuelvan.
Se volcaron en tres momentos diferentes 500 l, 25 000 cl y 82 dal de agua en un tanque cilíndrico
de 1 m de diámetro. Si el tanque se llenó, icuál es su altura?
5. Ordenen de mayor a menor. Escriban previamente todas las expresiones en litros.
2,5
4
-
42O cm,
- 0,075 kl - 3 dmt - ?,2 dal-
0,OOg
hl
6.
Resuelvan.
a. Un prisma tiene una base de forma octogonal. E[ perímetro de [a base es de 40 cm y su apotema mide 3 cm. Si e[ volumen es de 600 cm3, icuánto mide la altura?
b. El perímetro de la base de un cono es de 314 cm. Si la altura es igual a[ diámetro de la
base, icuál es el volumen del cono? Expresen e[ resultado en dm3.
c
El área lateral de un cubo es de 64 mm'?. iCuál es su volumen?
d. El volumen de una pirámide de base pentagonal es de 25,5 cm3. Si [a altura mide 6 cm, icuánto mide el área de la base?
7.
Piensen
y resuelvan.
Pilar quiere pintar un vitraux utilizando acrílicos de diferentes colores como indica el dibujo.
a. ZCuál es el área que ocupa cada color?
b. Si cada frasco de acrílico rinde 500 cm2, icuántos frascos de
cada color necesita?
2m
8.
Respondan.
a. Andrés llena una bañera con forma de prisma rectangular de L m de largo, 60 cm de ancho y
40 cm de alto para bañar a su perro. iCuántos litros de agua necesitará para llenarla?
b. Francisco construye cajas de aluminio de 50 cm de ancho, 70 cm de largo y 30 cm de altura,
sin tapa. 5i desea construir 2O cajas, icuántos m2 de alumínio necesitará?
c. Martín debe colocar dados de 2 cm de arista en una caja de 1,5 dm de ancho por 100 mm de
largo y 8 cm de alto. iCuántos dados entrarán en la caja?
d. Et termotanque de la casa de Pedro tiene forma cilÍndrica de 7,52 m de alto y 45 cm de diámetro. Si al bañarse consume 100 [, icuántos litros de agua quedarán en el termotanque?
Probabilidad y estadística
1. Escriban tres eiemplos de variables cualitativas.
2.
Escriban tres eiemplos de variables cuantitativas.
3.
Resuelvan.
)
5e encuestó a 25 personas al azar, para saber cuántas veces por día ingieren alguna fruta.
Los
datos obtenidos fueron los siguientes.
2; O;7;7; 5; 3; 2; 4; 5;7;3;3i 7;7;
a. Completen la tabla de frecuencias.
4;2; A:3;2; 2;7;7; 2; O;7
)
b. iCuát es [a cantidad promedio de frutas que ingieren por
día?
c. Calculen la mediana y la moda.
)
4.
Respondan.
Juan y Santiago están jugando a los dardos. En la siguiente tabla se observan los puntajes que
obtuvieron.
a. iCuál es el promedio de Jt¡an?
)
b. ZQué puntaje debe obtener Santiago para igualar e[ promedio de
Juan?
rr
5. observen y luego, respondan.
La tabla muestra el registro de temperaturas mínimas deI mes de junio.
a. Completen la tabla de frecuencias y realicen un gráfico de barras.
4
5
5
3
6
6
7
2
8
4
9
2
77
4
72
2
13
2
b. iCuál es el promedio, la mediana y la moda?
6.
Calculen las siguientes probabilidades.
Se extrae una carta al azar de un mazo de 40 cartas españolas.
a.
ZCuál es
la probabilidad que sea oros?
b. iCuál es la probabilidad que no sea un
c. iCuál es la probabilidad que sea un
7.
as?
rey?
Resuelvan.
a. Tres corredores participan en una competencia.
. iDe cuántas maneras distintas podrán llegar a la meta? iCuáles?
.
Si en [a misma carrera se inscriben cinco personas más, ide cuántas formas distintas pueden
llegar a la meta?
b. En un torneo de fútbot participan 12 equipos.
o Si un mismo equipo juega una vez por fecha, icuántas fechas deberá jugar cada uno?
.
Al finalizar el torneo, ide cuántas formas distintas pueden ubicarse los tres primeros puestos?
Números enteros
1. Escriban el número entero
que corresponda a cada situación.
a. Carla gastó $500 de sus ahorros.
b.Latemperaturamáximaenelmesdeenerofuede39oC.
c. Un pez se encUentra a 4 m de profundidad
d. Euctides nació en el año 300 a. c.
(-l
e.Marianodejóelautoenelsegundosubsuelodelestacionamiento.
f. Daniela tiene cinco mascotas.
)
2. ubiquen en la recta numérica los siguientes números enteros. Marquen con color el
opuesto de
cada uno de los números marcados.
-30; l-61; 18. -42i
3. lndiquen el nfimero que representa la letra a en cada caso. Erpliquen cómo lo pensaron.
a.
b.
4. Completen con
a.-s!-a
r. r
!
r-rr
(,)o=.
c.
-32O *u
a.
-s
!-rsr
e. -16
f. l-8t
o
C -9
5. Resuelvan.
a.
-3 + (+5) =
Í. -72 - (-l) =
b.8-(+9)=
s. -(-3) + (-a)
-
- (+20) =
¡. -18 - (-18) :
i-8*(+9)=
c.
-7
(+72) =
d. -76 + (+25)
e. -15 + (+7) =
h.72
-26
g. -567
h.
|
-234!
-+ro
-too
6.
Resuelvan.
a.3.(-2):(-l
b.
-7 . (-4)
8. 57 t (-19) =
=
c.-76.r=D
¡.
-740
:20
i. 418 : (-19)
=
:
7. Completen la tabla.
15
-3
5
3
0
-4
74
-7
-3
-7
8.
Resuelvan los siguientes cálculos.
a.t6-3.2+
15: (-5) =
e. -19
-
57 : (-3) + 18 . (-2) =
b.-ro: (-z)++.3-30:
Í.4 : (-2) + 72 . (-3) + 10 :
c.12- (rS-¡.2)-1.4:
g. (5 - 3 . 4) . (-0
d. 16
9.
h.2.(72-74:7)-3.5+2=
- 3 . 2 + (12 - 9. 3) : (-¡) =
Escriban el cálculo conespondiente
- ¡ . (z - 5¡ =
y resuelvan.
a. La suma entre el opuesto de -20 y el doble
del opuesto de 5.
b. La diferencia entre -15 y el móduto del
opuesto de 6.
CoNTRoL DE REsurrADos
18.
L Slstema de numeraclón
declmal
2,
b.t;
c,7;
4
3
4
d.9;8
c,3
d,62
e,2
t.
lL
L223
m.27
n,76
110
Por ejemplo,
¡.
a.529
b.7296
m.
a.3200
<.
Por ejemplo, a.251, 9
MEÍ{TEAITIVA
Solución a cargo del alumno.
0, ilultlpllcaclón y dlvlslón.
Propledad dlstrlbutlva
a,72
b. 6
c. 8
d. No se puede,
7.
e. No se puede, 30.
i,27
7.
Por ejemplo, a.
a,75
b. 13
F.
1
168 : 6
:
96:6+60:.6+12l.6=28.
3. Potenclaclón y radlcaclón
tt,
Por ejemplo, a. 49.
la quinta potencia.
tt.
Por ejemplo, a, 5i 3i 125.
Por ejemplo, a, 3; 3 y f. 1000;
3;1000.
a.728 e.76
b. 1000 Í,6
c8
9.5
d.729 h. 5
l.
18
l.
60
Operaclones comblnadas
17.
8
10
4t,
Por eiemplo, a. puede ser 5874.
u.
.77 c 32 . !72
b,23.3.52 d,2.32.5.72
a.23 .32
e,298
¡.24
tt6,
Solución a cargo del alumno.
1500
b.2
c.75
G.
d,7500
9.7
h,152
Múlüplo comf¡n menor y
dlvlsor óomfin mayor
47.
a,240 d. 50
b.9400 e.7488 h.6
c,64 f. 1300
g. 1500
30.
Por ejemplo,
¡.
=.
46 b,79 c,7
d.22
60
840
e.364
c-
a. mcm
= 52920, dcm = 4
c
:2340,
b. mcm : 2000, dcm
mcm
:
dcm =
20
1
48.
762
d.28
Solución a cargo del alumno.
34.
a.
820 c. 60
b,722 d.170
f.
c.
d.
28,
a.
92.
a.
b.
5
b. 866
t3.
16.
a.2
b. 1
e. 2,3,
45.
s. 485
a.
tt.
6
Por ejemplo, en la fila 1 va X en:
27.
37.
F.
9.3
h.6
¡. 1000
7,2, 4,5,70.
29.
12.
Por ejemplo, a. Dos elevado a
14.
Por ejemplo, a.
98 727;72789.
Í.
d.7, 2, 4, 5,70,20
a.VaXena.
28;
1,160
e.
b,32
c,705
d.9000
c.7,2,3,
Solución a cargo del alumno.
10.
Por ejemplo, fita
t
26.
rc.
67
45
a.774
a, 723, 726, 729, 732, 735, 738
b. 208, 276, 224, 232, 240, 248
25,
Í.63
J.40
42.
d. 506005
Por ejemplo, fita
e.37
9.
Por ejemplo, a.
408004
b.4008004 e.48005
c. 5 000005 f. 48008ó
crb.>d.tf.r¿>e.
24,
c,74
d.9
d.792
S. Dlvlslbllldad y hctorlzaclón
lrrucmc¡ór le.:l+
23.
a.
¡. 6
c 3072 e,2
41.
205356
10000 e.2
d.5
Por eiemplo, a. 16.
22,
5.
c.56
t9,
Solución a cargo del alumno.
Va X en d., e., g., l.
c.
b.275
2t,
4,
b.8
a,72
38.
733
20.
Solución a cargo del alumno.
E.
10000 Í,67
8
9,22
h.743
1.326
b.627
3.
6.
e.625
f.
a.77
Por ejemplo, a. con 3.o opción.
a,5;
d.
t9.
7,
37,
c,6
a. 10
b. 10
35,
Por ejemplo, a.
F.
36.
Por ejemplo, a. 5, 48.
e.290
i.470
a. Cada 60 minutos.
b. 60 paquetes.
c. Et 13 de junio. No. Sí.
d. Para 6 amigas.
7. lenguale slmbóllco.
Ecuaclones
49,
Por ejemplo, a. 2a.
50.
Por ejemplo, a. con 2.o opción.
57.
Por ejemplo, a. Et doble de [a
diferencia entre un número y
cinco es igual a 35. x: 73
52.
d.a:lZ
a.m=!7
b.t=16
c.x=8
e.y=4
f.n=100
53.
ax:0
b.x:2
c.x= 25
d.x=87
e.x:0
f.x=6
g.x:8
*.
ex:5
b.x=9
c.x:15
d.x=12
h.x=3
i.x:32
i.x:2
k.x:72
Lx=1
m.x:4
n.x:4
6.
a.14años.
b. $60
tl, Fracciones equ¡valentes
c"4kg
d.864 panchos.
f.x=2
g.x:0
h.x=7
55.
ax=6
b.x=100
67.
a.
x:36
b.x=15
G. x = 13
e¡erpto
d. x = 24
e.x:0
f.
68.
a-x:729
x:'22
ax=8
b.x:4
Por eiemplo, a.
Por ejemplo, a.
IL
Por eiemplo, g.
Í.x=36
13.
Va X en
2.107 + 6.106 + 6.7O4
rrrEGRAoóil S{'7
20 000 000 + 6 000 000 + 60 000 +
2000+2OO+6
T'.
57.
a 2850 b.5028 c8o25
5&
¿779
a
Sí. Sí. No se sabe. Sí. No se
sabe.
b.3. Por 10.
c- 507
d.34 . 5 .7
¿ 22 .72 .73
172 .77.73
..23 . 52 .7
b. 3 pastitlas de antibiótico
Y4
del analgésico.
b.25 .3 . tl
(.22 .54
mcm
=
27OO; dcm
=
762 . (x + 25) = 784' 2
-
t¡;
: 79
Por eiemplo,
6¡t.
.-792,
728,
a
E. O¡dm
Resto 12.
20, 40, 60
6/L
a
mcm = 900, dcm = 30
b. mcm = 1400, dcm = 5
c. mcm = 72O, dcm : 4
d. mcm = 1309, dcm = 1
e. mcm = 6300, dcm = 2
f. mcm :729, dcm = 27
65.
e. Cada 30 meses. b. 150 moños.
y representación
L
Solución a cargo del alumno.
L
V.
320 I
a {.
c.= d.(
af
b-+
'+ d-f.
i"i
b.3
b.8 ,? ¿.2
t+ e.2o6
d.
31
1.42
m.
Regaló 18. Aún conserva 27.
b. Le quedan aún 13 litros.
c7260
d. Por 24.
6L
del pasa¡e.
b. I
a
b.1023
6L
¡.105
b. 1
jf
a)
a.5
x
r.7
..#
'#
d-+ r.t
Por eiemplo,
19.
45
60.
1 103
Llegó
',
".
15.
17.
Cada 24 horas.
7t.
59.
b.á
a
t6.
b.23
74.
a
2
a.f
2 . 10000000 + 6 . 1000000 +
6 . 10000 + 2 . 1000 + 2 .700 + 6;
I
7, 2, 4,7,74,28
b. 1, 3, 5,9, !5, 45
c 30, 45, 60,75
t4'
+
2.703+2.7O2+67Oo:,
56.
fr.
b.9 d.l
e.x=81
7L
TETTEAf,tla
f.
";? 't
d.x=8
AI'TOEYAUTAG|Óil
Solución a cargo del alumno.
j.
racionales
d.x:1
ax:8
b.x:5
c.x:1
(
E. Operacionss con números
Gx=1
7t-
,..8,8.
10.
b.x:1
ax=8
j.
9.
b.x=34
69.
c.x=10
d.x=15
Por eiemplo, a.
8'Po,
70.
e.x=1
7.
edL
b.8
, '+
o.t
'\
3'Por
"¡"rplo,
+r.l.l.1
"'?
a o*.
t'*? b.?
'+
2'5',4'5
t,t,?
^¿,+,?,3.?.f .t,!
c
Alquiler e impuestos $+sso.
Otros gastos $¡ Z:0.
"*tr '+ '# 0.1
\q b-+ .Z d.+
a.
a=
2+
-
b.)
eor eiemplo,
c)
a
con
+.
d.(
+=Z
2t.
a
Quedan 55 bombones.
b. Continúan 7 alumnos.
c Quedan 525 libros.
TEITIEATNYA
Solución a cargo del alumno.
(
ll. Potenciación y radicaclón de
fracciones
26.
Solución a cargo del alumno.
27.
Solución a cargo del alumno.
4t
28.
43.
Solución a cargo del alumno.
_
a.t c.]
e.j
b.+ d.t+ Í.4
58.
a.2:70;7:5.
a. 4;2OO; 5;720
b. tl; toz;340;336
b.775 :700;7 : 4.
c.7; 63; 7; 705
42.
Solución a cargo del alumno.
ry.
Solución a cargo del alumno.
u;.+
b.; ,ffi o.# o';.a ,.¿
".+
a.S
a.l
rl
r'
,.3.'
".#
30.
4.
MENIEAI?IVA
'a.4 ,.+
b.3 a.]
Openciones combinadas
con fracciones
,+
^.+
".4
a.fr a.ft rfi
37.
32.
^
lto
páginas.
f,
b.+
.#
tt;.r.l..In+]n:zn
a.
o.l
34.
^, -1.,
a.(
35.
_
".;
b.=
a.j
=
r-)
d.(
E.x.E.n.E
3&
Solución a cargo del alumno.
*;.
a.10 niños.
tt;.¡.=
".t
d.2
á a.l ,.4
l^,,r=#.
a.ns=ftm,
J
$465,70
g272,os
a.
4,2i
i.
1,08
d. $4,97
e. 9189,28
63.
lf.
y expresiones
53.
Por ejemplo, a. 0,25 y b. 0,33...
54.
Solución a cargo del alumno.
55.
<.
56.
Va X en a., b., d., f., g.
Hay infinitas posibilidades. Por
ejemplo, a. 1,6.
O,7
0,39
d.
4,735
e.9,9
Í. 4,23
c.
O,2
4
¡.3,2
d.
e.0,4
64.
Por ejemplo, a. con 0,3. y
g. con 2.
65.
Por ejemplo, tabla 1, fila 1: 0,2;
0,02.
66.
a,0,064 g. 0,9
b.3,67
h. 0,3
c. 0,00001 ¡. 1,5
d. 1,27
i.7,3
e. 0,343
k 0,2
¡.8,47
L O,7
a.ns=frn'
u.$,.+ a.]
10,8 c.2,5
b.3,739
a.
57.
a.
a.
68.
Por eiemplo, a.
".i3
a.
67.
52.
-
Í.7,79
g. 0,89
h. 1,04
61.
.e=f,'
Fracciones
decimales
Solución a cargo del alumno.
a.t
a.fl
50.
a.fr
MENTEAITIVA
-
c.$ttte
;.+ b.3 .. #
a.74,98
b. 8,807
c. 54,47
d. 18,906
e.2,487
a.
b.
aet total. 2z fotos.
49.
..+ a.ft
+-# ":?
;.+
t
t! r
..#
r.fr
rnr¡emcút
-
60.
62.
".n
r.ft
b. $216; $roe; $zz; $¡e
c. Sobraron 9 porciones.
d. 12 de un ambiente, 32 de dos
arnbientes y 4 de tres ambientes.
+
u.f, 'a.t
t';.+.rc+j.B:+
t9.
a.
\^,
";.x
,.?
48.
Operaciones con expresiones decimales. Porcentaje
c. $406,80
47.
It.
jf; $; o,e.
It+.
b.
c<f.<a.<e.<b.<d.
Solución a cargo del alumno.
59.
Por eiemplo, fila r:
25,75
20
35
c.20
a.
b.
69.
a. 4,8
b. 58
c 520
b.36,7
d.
20
5
f.30
g. 300
e.
h.6
¡.3
d.97
3850
g. 650
e.
h. 700
Í.726
70.
a. $284,4
b. $408,825c 40 chicos de otras escuelas.
15 chicos organizaron la fiesta.
I,TENTEAITIVA
Solución a cargo del alumno.
lS. Operaciones combinadas
71.
Por ejemplo, a.
<.
.".+
u.f r.ft
,. ,+5 s. o
";.+h.
t.ffi
i.ft
90.
r. fia
n.ffi
d.ro*E
ruro¡vlluncÚil
ufr
¡mremc¡ót l¡.lr.m
73.
Solución a cargo del alumno.
74.
a.
^
]: o,zs
a.
o,G
c.
$ = o,tts
j:
tt;.# u.f c.1 a.!
a,7O2;750 b.80;32
Va X en a., b., d., f., h. e i.
Solución gráfica.
b.k:7
15.
b.sí.k=25
<.
#
n.t a.f ".1
t.l
";.?o
tt;.4
s.ffi
..
S
u.
79.
Cliente
lG. Gráficos
2.
a.]
".+
4.
b, $792,55. Necesita vender 10 kg.
80.
c
b. 4950
82.
1.o escala: 13,5olo;
2.o escala: 19,2%; destino: 67,3o/o.
a.74
b. 5,5
c. 18
d. 60
e.25o 1.75
f.20
¡. 900
5.44 k 96
h.675 [ 1950
7.
c. Solución gráfica.
(7;5)
(a;8)
kg
días.
c.2 kg
d. 188,55
TilTEGRACTóil E.t7.tE.tC
Solución a cargo de[ alumno.
d. No, siempre
b.150
aumentó de
peso.
E[ ingreso disminuyó.
17. Fundones
9.
e.72,Q4
b. Si son variables inversamente
proporcionales. k = 8000
t9.
a. 0,5
f.
87.
102,8
a. a :
b. b :
a. Solución a cargo de[ alumno.
b. En el mes 12. En e[ mes 18.
c A mitad de año.
d. Sotución a cargo del alumno.
e. Solución a cargo del alumno.
a.3750 c.96;24 e. 160
Í.94
b. 8000 d.70
b. 35,86
c.29,24
a. Fila 1: 200. Fila 2: 64, 25.
8.
8ó.
a.
Va X en b. y c. Sotución gráfica.
18.
a. Tardó 30 min. Estuvo 30 min.
Tardó 20 min.
b. Tardó más para ir.
VaXena.yb.
Pantalón: $232,4; Gmpen: $280.
t7.
Solución a cargo del alumno.
6.
2O"/o
85.
88.
(5;ó),
a. Por ejemplo, fila 1: 14.
b. 0 horas; entre las 2 h y las 4 h.
c. A las 11 horas. Fue de 24 oC.
d.7520
e.
c.2Oo/"
a= (2;2),6: (4;0), c:
¿=(0;ó),e:(8;2)
5.
83.
a
t6.
Solución a cargo del alumno.
¿. = (3;6)
e. f" = (2,5;5)
Por eiemplo, fita 1: 3; 3,5;3,49.
91,7"/o
inversa
c.c=(0;3)yd=(7;o)
10,2 cm
81.
a.77,7
19. Funclón de proporclonalldad
3.
$262,8; cliente 2: $146;
a.18,2 cm b.8,ó cm
y tabtas
t.
Solución a cargo del alumno.
!,
cliente 3: $lg+,2
84.
Solución a cargo del alumno.
73.
a. Por eiemplo, fila 1: 250.
Por eiemplo, a.
b.
72.
a. Por ejemplo, fila 1: 7.
76.
a
lE. Función de proporclonalldad
directa
74.
a.ff
^.{
75.
a. Fila 1: 7, 2. Fila 2: 75,25.
b. Solución a cargo del alumno.
c. Sí, es correcto. d. Sí.
VaXenb.yc.
92.
93.
0,7 <o,t <0,9<0,04
77.
89.
Solución a cargo del alumno.
Solución a cargo del alumno.
10.
VaXend.,e.yf.
20,
Solución a cargo del alumno.
27.
a. y b. solución a cargo del
alumno.
c
En
a es único y en b., no. (4;1)
22,
a. Puntos mal ubicados: b, c y e.
b. Sotución a cargo del alumno.
23.
a. Solución a cargo del alumno.
b. Sí.
c. Sí.
24,
Solución a cargo del alumno.
25,
a Fila n 7. Fila 2:77,50;37,5Q;35.
b. Solución a cargo del alumno.
26.
a. Solución a cargo del alumno.
b.Sí.k=3
27.
a. $rso
b. Por ejemplo, fila 1: 300.
c.k:150
d. Solución a cargo del alumno.
2A.
a. 10
¡
,
22.
7.
b. 35
c. lnversa.
b. Pirámide de base triangular.
c
d. Por eíemplo, fila 1: 70.
e. Sotucíón u .urgo del alumno.
29.
ADP b.NP cDP d. DP
f. Pirámide de base hexagonal.
d.AyE;EyF.
23.
8.
VaXenb.
a.10 horas.
b. 4 horas.
c. Estaban a 160 km del hotet.
d. Sí, a ta ida.
e. Duró 2 horas.
a.ll
c.I
e.l-
b.
d.
f. r-
r_
Solución a cargo del alumno.
Va X en:
a. Prisma de base triangular.
b. Pirámide de base cuadrada.
c Prisma de base triangular.
25.
Solución a cargo del alumno.
26.
Solución a cargo del alumno.
10.
a. El cuerpo está formado por
31.
A. Sí.
b. k = 800.
La variable indepen.
diente es [a altura. La variable
dependiente es el volumen.
c. Fila 1: 50, 60.
Fila 2: 32000, 56000.
32.
a. Cada uno deberá pagar $150.
Si fueran 30, deberia pagar $ZO.
b. Son variables inversamente
proporcionales. k = 2100
c. Fila 1: 27; 28. Fila 2: t5O;70.
ll
24.
9.
30.
c. Uno solo.
d.
AUTOEVATUACóN
27.
a. 6; pentágono.
b. 18; hexágono.
c. 7; pentágono.
11 cubos.
b. No.
No.
e. Habría que agregar 6 cubos
más. En el centro del cuerpo.
11.
24.
6:6;70:6+6:70+2
29.
VaXena.
VaXena.,b.yd.
12.
Solución a cargo del alumno.
30.
VaXenb.
13.
VaXena.
MEI{TEAITIVA
)
Solución a cargo del alumno.
[0. Clasiñcación de los cuerpos
1.
c. Cono. cilindro.
d. Prisma de base hexagonal,
cilindro.
e. Prisma de base triangular,
pirámide de base triangular.
f. Prisma de base rectangular,
prisma de base triangular.
¡lrTEGRACIór{ eD.¿}A¿.e3
Por ejemplo, en a.
d. con
6.
5.
12.
20.
5.
Por ejemplo, fila 1: solución grá-
fica;6;8172;6+I=72+2.
tX. Desanollo plano de cuerpos
6.
Solución a cargo del alumno.
b. Dodecaedro;20.
c. 8; octaedro.
d. 4; tetraedro.
20.
a.5í.9+9:!6+2
b.Sí.7+70:75+2
2t
VaXena.yd.
a.6'
b.2702',
c.I82'
36180"
d.220"
d. 900'
a
y b. con 32o 25' .2
a.7040 34'
c.75" 48' 52"
b. 90 53'15" d. 2380 37',75"
75'
d.7720 42'
b. 150 50' 20', e. g70 40' 25"
c.920 70' 30" Í.42" 20', 30"
a.37o
6.
a. 74'; 50"; 47o C. 45'; 77oi 0"
b.3';7"; 44o d. 44') !"t 43o
a. 12; cubo.
e. con
c
Por ejemplo,
4.
F.
79.
a.1380"
b.72oo"
3.
18.
Va X en b., c., e., y f.
c, con
2.
d.DyE
77.
Por ejemplo en b. va X en un
cilindro, un cono y un prisma
de base rectangular.
3.
8.
4.
c.CyE e.AyD
76.
Solución a cargo del alumno.
Poliedros regulares
a. con
b. con
1.
a.AyB
b.ByC
cuadrada.
b. Esfera, cilindro.
4.
14.
15.
a. Cubo, pirámide de base
ll.
Operaciones
infinitas rectas.
2.
_
¡
t
!+. Sistema sexages¡mal.
t3. Punto, recta y plano
Por ejemplo, en a. va X en
Solución a cargo del alumno.
)
Pirámide de base cuadrangular.
d. Cono.
e. Prisma de base pentagonal.
AUTOEVALUACIóN
)
a.C,DyE.
b.AyB.
c.FyA.
a. Prisma de base rectangular.
tS. Ángutos complementarios y
suplementarios
7.
a.(
b.(
8.
VaXenb.yd.
c.:
d.)
9.^A
a.&:37";F=53o
23.
b.ff:ra";t=72.
c. t : 30"; 6: rso"
24.
Solución a cargo del alumno.
7.
^^
b.6=íi=75o;g:t5";
10.
tG. Angulos adyacentes y
opuestos por el vértice
11.
..4=á:ur.,fi=f
d.ft:a=2q";fi=fi:roo"
Por eiemplo, en fila 1 va X en:
consecutivos, suplementarios y
12.
13.
Solución a cargo del alumno.
26,
a.34o
b. 560
c.
d.
90o
280
e.73"
Í.22"
50'
b. 550 38'
veces. d. A veces.
b. Nunca. e. Siempre.
c. Nunca.
a. Paralelogramos. Tienen dos
diagonales.
6=50o
Solución a cargo del alumno.
b.
tB. Triángulos. Elementos y
prop¡edades
18.
a. y b. Solución a cargo del
alumno.
1.
a.i=42o;
f
a.ac:6cm;t=45"
a. Cuadriláteros.
b. Cuadrado; rectángulo; para-
l.df=7-cm;'ei
c
:f=39";
: 1020
2.^,.
d
c=5/"
b. x = 12o; ^
d
f:37o
:
ii^ = 1030;
40o;
-
b. A = 2oo; A = 160"; 6 = 90";
c. x
t. = 70'
á=95" A
A
j=37";
^ ^ =1ooo c.[i *é:ro"
a.&*[i
[:
t3.
k:53o;
Construcción de triángulos
V.
4.
22.
c.92o 45'
rZO.;
-
Por ejemplo, a.
Solución a cargo del alumno.
25'
b.19o
90o
A
ij :
3.
2t
a.620
23o: A" = t45o;
d.x:15o;
20.
¡.&*8=1800
=
d. 660 50'
e. 1070 30'
lelogramo; rombo.
lsósceles.
d. Rectángulo; escaleno.
a.x=5o;á=38o;b=85o;
=ue"; &.=21
En e[ trapecio isósceles las
diagonales son iguales, en los
trapecios rectángulos y escalenos, no. No, en ningún caso.
72.
^A
c. Llano; perpendiculares; recto.
19.
Solución gráfica. Existen muchas
posibilidades.
a. Dos diagonales.
ut. = 90o; m6a = 7350;
: zzo ¡o'; ctt = 670 3o'
TNTEGRACóI{ A\.ffi .AG.e7
b. Depende del paralelogramo. Sí.
c. En cuadrados y en rombos.
11.
30.
".
r6t
Solución a cargo del alumno.
"a.á=6=130";t=á=so",
9.
10.
29.
Solución a cargo del alumno.
MENTEAITIVA
a. Por ejemplo, en fila 1: B, F, .l;
31. Constn¡cción de cuadriláteros
a. A
\= 2so; fi = es"; & = 65o;
17.
Solución a cargo del alumno.
8.
da:2cm
AAA
b. j= 126oik = 360; i = 72o;
jk:4cm;ij :3cm
24.
15.
76.
a., b., c. y d. Solución gráfica.
lE. Cuadriláteros. Elementos
y prop¡edades
No hay; No hay.
b. sí. sí.
AUTOEVATUAClÓN
27.
a.1630
t7. Mediatriz de un segmento
y bisectriz de un ángulo
74.
Solución a cargo del alumno.
Solucíón a cargo del alumno.
adyacentes.
¡A
d.y=136';O=44o
It/IENTEA[TIVA
=11s"
25,
745";35.
a.&=4oo;ii:r+0"
b. 6 = 81o; A: 81o
c.ft=150o;t:rso"
,Solución a cargo del alumno.
& = 105'
b.x=67030'
Por eiemplo, fila 1: 1450;
Solución a cargo del alumno.
6.
0 = 138'
a.f:+e";k=t32o
it.x=39o
5.
Sotución a cargo del alumno.
a. Solución gráfica.
b. No. No se pueden construir
triángulos equiláteros rectángulos
ni obtusángulos.
13.
Solución gráfica.
14.
a. Sí. Los ángulos de las distintas
figuras que queden consecutivos
deben sumar 3600 o 1800.
b. Con rombos y trapecios.
--1.t=0=zo.;?=nn:no"
15-
b.fi=6=102o;fi:sz.;
6 :104o
;. 4 =$ = 6oo;^t =^á = rzoo
d. i= k :42o; j = [ = 1380
MEI{TEAITIVA
Solución a cargo del alumno.
t]{TEGRAC|ÓI{ eB.A9.t0.3t
16.
a. No; No; Sí.
b. Escaleno obtusángulo.
)
31.
Solución a cargo del alumno.
a. El "A" es convexa regular, el
b.2
"B" es
18.
79.
más.
alumno.
c. No son posibles las construcciones del rectángulo y del
cuadrado.
a. Mariano y Georgina.
b. Solución a cargo del alumno.
c. Suma de ángulos exteriores.
Sí.
b.
h. 0
e. Eneágono. 40o
b. 24";7560
j=64";k ^273"; l=33o
fi : 32o;'i : 23t"; 6 = 2503
0=6¡'
51,
d. ?
52.
t:77o
35. Construcción
regulares
34.
AUTOEVATUACóil
Solución a cargo del alumno.
a. á : Z0o; 'ü = 32": t : Ze"
b. ñ = 84o; f, = 7240; 6 : 28o;
polígonos
6=
724"
i. ? = 98';
t=30'
744O;744;36.
t :72"; t
Por ejemplo, a. V.
Sí.
Sí.
c.
d.
-ef
= zso;
t6.
Sí.
e.
Sí.
No. f. No.
g.
No.
= E^: il.^= 7,2
3G. Perímetro
37.
Solución a cargo del alumno.
'i:75";d:b=1050
cm;
Solución a cargo del alumno.
Por ejemplo, a.
2.
3.
Solución a cargo del alumno.
lfl.
Círculo y c¡rcunferenc¡a.
Elementos y prop¡edades
27.
a. Una circunferencia. El centro.
El radio.
b. Tiene e[ mismo centro, pero
distinto radio.
c. Se forma una circunferencia
del mismo radio, pero con el
centro corrido.
d. En b., son concéntricas. En c,
son iguales, pero no concéntricas.
28.
Por ejemplo, a. con e[ diámetro.
29.
Solución a cargo del alumno.
31. Construcción de circunfurenc¡as
30.
Solución a cargo del alumno.
TNTEGRACóil 3A.33.3r+.3S
N,
4.
b. y b. solución a cargo del
alumno.
c Alineados.
5.
47.
Solución a cargo del alumno.
a. Mediatrices o diagonales.
b. No.
46.
a.
O;2;5;9
b.74.20
47.
Por ejemplo, a. V.
d.47,42
8.
cm
a,0,032
b. 5 000
a.77
b.2O
44.
Solución a cargo del alumno.
45.
Solución a cargo del alumno.
c
b.22,28
a.7,2
7.
43.
a. 15,3 cm
6.
42.
Solución a cargo del alumno.
F.
a.72cm c.5cm e.4cmy
b.72 cm d.24 cm 72 cm
Solución a cargo del alumno.
32o
área de figuras
1..
39.
MEf{TEAffiIVA
y
planas
38.
3=65o;f:h=115o
26.
)
de
Decágono. 360
Solución a cargo del alumno.
c.29o;6!0
d.40o; 50o
25.
a. a¿ = 4.cm; ab = 6 cm;
¡A^
x:
: nef;t: 106,i t : ue",
Por ejemplo, fila 7:
No.
c. Triángulo. 1200
d.
: B4o; 0 = ttTo;t = 128o;
24o
35.
23.
a. 30o;30o
b.
a. Polígono de 15 lados.
b. Heptágono,57,420
d:tt2o; ij:95o; f=86o
c.
21.
)
50.
a. á = 140o; i = r+t;; t. = t37";
Sí.
20.
a. y b. Solución a cargo del
24.
a.
b.
Sí.
33.
b. 36 triángulos
22.
a. Sí.
a. siempre c. a veces
b. a veces d. nunca
cóncava irregular.
c. Se forman 5 triángulos.
Sí.
49.
b. En ambos casos es 900o.
Solución a cargo del alumno.
¡
,
alumno.
c.
32,
a. Sí.
a. y b. Solución a cargo del
3t+. Polígonos
77.
a.7
$.
b.
42 cm
cm
c. 0,03
d.92
10
c.23
dm c 9,42 dm
cm2 d. 30 cm,
a.9cm b.8cm c.2cm
a. P : 27,64 cm; Á. = 2O cm2
b. P = 27,42 dm; [. = 50,13 dm,
9.
a.7,74
b.74,2
10.
a.10
cm2 c 37,5 cm2
cm2 d. 9 cm2
dm
b.9
cm
TIEilTEAITIVA
Solución a cargo del alumno.
37. Area lateral de prismas,
piÉmides y cilindros
Por ejemplo, prisma de base triangular regular se une con b . h . 3
Uf
. z.
72.
a. AL: 80 cm2; AT: 88 cm2
b. AL: 30 cm2; AT: 39 cm2
c. AL: 62,8 cm2; AT: 87,92
d. AL: 36 cm2; AT: 56 cm2
cm2
dm2
b.6,59
c. 0,16
dm'z
76.
a.286
m2
b.x=10mm
b.464
m2
18.
a.72,56 I
b. 3 baldes. Gastará $240.
79.
a. 400 listones.
b. 216 cm2
lB. Unidades de capacidad y
un¡dades de volumen
20.
Por eiemplo, a. F.
a.250 c.32OO e.28
f. 135 000
b. 1
d. 18
22.
a. Compró 15 botellas de gaseosa.
b. Conviene la de 1 litro.
c. Sí.
d. Tres frascos. Sobran 10 m[.
e. 6,9 I de cloro por semana.
MENTEAI?IVA
Solución a cargo del alumno.
19. Volumen del prisma, de la
piÉmide, del cilindro y del cono
cm3
b.0,6594 cmj
c.42 cm3
d,777,75 cm3
e. 27,25 cm3
f.
1,13 cm3
d.n.d.h
b. lgual.
e. 12.6
42.
288
m2
43.
4,99
c
a.24 cm3
b.5cm
80,07 cm3
d.3cm
cÑ
b. 100
a. 75
t+0.
Vadables, población y
7.
Por ejemplo, fila 1: Cuantitativa.
INTEGRACIóN 38.37.38.]9
2.
30.
c. 13
b. 600 cml
muestra
MENTEAITIVA
cm
b.27 cm
litros.
cm3
Solución a cargo del alumno.
a. Población: chicos de entre
d. 10 dm'?
e. 4 m1
a.16
m2
Ir4.
29.
a. 30 velas. 9000 cm3
b. Necesitará 3 000 cm3 de arena.
12
y 20 años. Muestra: 350 chicos.
b. Tipo de videojuego. Cualitativa.
cm2
3.
31.
Solución a cargo del alumno.
32.
\1. Recolección y organización
de datos. Tablas
a. !3,76 cm2 c. 18 cm2
b, 14,72 cm2 d.79,25 cmz
a. AL 24
b.
cm2; AT:
40
4.
cm2
a River:8;
Boca: 7; Racing:4;
San Lorenzo: 4; lndependiente: 2;
Otros: 3.
b. Equipo de fútbol. Cualitativa.
AL: 725,6 dm2; AT: 282,6 dm2
c. AL: 90 cm2; AT: 720
33.
a.226O,8
b.7,5
cm2
cm2
c. 20 caias.
c. River.
d. Cuatro clubes. San Lorenzo,
m2
Racing, Boca
34.
a.4cm
b. 360
cm3
5.
35.
a. 98
b. Largó: 27 cm. Ancho:27 cm.
36.
a. 22 alumnos. c. 33 conos.
b. 72 bolsas. d. 3 cm
37.
a. Largo: 20 cm, ancho: 2 cm
alto: 2 cm.
Y
b. Podrá contener 160 caramelos.
a. 0,04
dm
b. 1 884 cm3
39.
a.97,4
a. 17
y
River.
a. 4;3; 6;2;7;3; 2;7
b. Nota del trimestre. Cuantitativa.
c. 28 alumnos.
d. Aprobaron 15 alumnos y
desaprobaron 13.
e. 13 alumnos.
f. En diciembre deben rendir
12 alumnos y en marzo 1.
hE. Frecuencias absolutas
y
relativas
6.
a. Por ejempto, fila 1: 5; 0,725;
38.
40.
23.
a. Suma.
c.n.l
Alto: 12 cm.
27.
a. 108
I
4:9; 2; 3
a.56,52
dm2
a.x:2cm
b. 30,24
a. 50,24 cm];773,04 cm3;
25,72 cm3; 37,68 cm3;37,68 cm3.
28.
74.
a. AL: 60 cm2; AT: 76 cm2:'
Prisma de base rectangular.
b. AL: 188,4 cm2;
AT 244,9 cm'?; Cilindro.
c. AL: 112 cm2; AT: 767 cm2:
Pirámide de base cuadrada.
d. AL: 96 cm2; AT: 744 cm1'
Prisma de base octagonal.
77,
t
41,
26.
b.
Necesita 467 venecitas.
a. 4,8
25.
a. 25,72
27.
13.
15.
AUTOEVALUAC¡ÓN
Por ejemplo, fila 7: 24; 24.
11.
y con Área lateral+
24.
b.62,8
cm2
b. Mapuche, porque es el que
tiene mayor frecuencia. 37,5"/o
c. Los tobas y los diaguitas.
d. 4,5 cm
b. 24000
litros.
72,5.
c. Q,92 cm
c. 5 cm2
d. 5 cm2
7.
a. Por ejemplo, fila 1: 3; 0,77;
76,67.
b. En ritmos.
c. Elongación.
l+3. Gráficos
25.
a. Cantidad de pájaros.
8.
Por ejemplo, a. 50; 180.
9.
a.25 b.20 c.75
d.60
10.
Solución a cargo del alumno.
71.
a. Cualitativa. A 65 personas.
b. Solución a cargo del alumno.
t2.
a.10 en el A,12 en e[ B y 15 el
b. En el B.
c
C.
38 varones. 75 alumnos.
13.
Solución a cargo del alumno.
74.
a. Solución a cargo del a]umno.
b. Se encuestó a 72 personas.
15.
a. En la sala B, hay 6 000 libros.
b. En totat hay 18000 libros.
a. 13 millones de habitantes.
26.
a. Solución a cargo de[ alumno.
b. En [a de hombres, sí. En la
de mujeres, no.
c. Solución a cargo del alumno.
l\.
Promedio, mediana y moda
27.
a. X = 38,29; m" = 38; mo = 38
b. x : 29,3; m" : 28,5; mo = 28
c. x = 34,74; m" = 34; mo: 34
d. x = 42,7; m" = 30; mo: 72
28,
x: 3,27 m" : 3,5
fro
:
29.
a.76;76
b. 18; 19
En a.
c,77;77
d.76;73
y b. las soluciones no son
INTEGRAOÓN hD{+l.rA.\3
5;9y6;8y7.
a. Representa la muestra.
b. Cualitativa.
19.
a. Cantidad de paquetes vendi-
Cuantitativa.
c.
33
d.72o/"
23.
a. Solución a cargo del alumno.
b. 29
d.34,5Y" f.79
c.73,8o/o e. 6
24.
a. Solución a cargo del alumno.
b.
25o/o ajedrez
y
76,670/o damas.
a.X=5,ftffi"=5;ño:4
b.x=7,5;fr"=7i ffio = 5
c.x=7;m"=7,5;mo:10
42.
a.i=8,23;m":8;fi.=8
c.
No.
43.
Va X en:
b.7,60/o
c. 0,24
44.
b.2770 d.4
0,25 e. Solución gráfica.
32.
d. cara-cara; cara-ceca; ceca-
22.
a. Por eiemplo, fila 1: 3; 0,06.
b. Cantidad de cargas por mes.
13 años; bimodal, 12 años
y 14 años; m" = 13 años.
d. Solución gráfica.
c.
c. cara-cara; cara-ceca; ceca-ceca.
a. Deporte preferido. Cualitativa.
b. Natación, en el grupo A y
Básquet, en el grupo B.
0,375; 37,5.
a. Por ejemplo, fila 1: 0,27;27.
alumno.
21.
7:.
b.24
c. x =
Probabilidad simple
a.7; 2;3; 4; 5; 6.
b.2;3; 4; 5; 6;7;8;9;7O;77;72.
a. Sexo y estado civil. Cualitativas.
b. y c. solución a cargo del
alumno.
d.33,330/o
a. Por eiemplo , frla
3t
VaXena.,c.yd.
dos. Cualitativa.
b. y c. sotución a cargo del
20.
m":50k9
40.
a. 10
+S. Experimentos aleatorios.
18.
TNTEGRACóN bh.|{S{r6
39.
a. Peso. Cuantitativa.
b. X: 50,83 kg; m" : 50 kg;
mantienen. x = 36,30.
c. Hay varias posibilidades: 10 y
No.
MET{TEAITIVA
Solución a cargo del alumno.
b. La moda y [a mediana se
30.
19 puntos entre las dos pruebas.
b. No.
a. Europa.
a. 7320 maneras distintas.
b. 440 maneras distintas.
c. 60 maneras distintas.
47.
1
a
t7.
)
Cuantitativa.
b. 37,25; 72,5; 37,5; 78,7 5
c. Solución a cargo del alumno.
d.15 pájaros. e. 4,5 páiaros.
únicas.
76.
b.
38.
cara;- ceca-ceca.
";.# ,.#
b.+ d.+
t+6.
".+
r.+
c.EnelA.
: ].
Cálculo comb¡nator¡o
52,92 mm; me
:
43,5 mm;
mm
b. Solución a cargo del alumno.
t+6.
47.
Por eiemplo, a.
*;.+
b.*
c.9
36.
a. 60 números. 24 son pares.
b. 12 números son múltiplos de
5 y 36 son mayores que 500.
37.
De 28 maneras distintas.
ffi.
,.#
d.#
49.
a.72 .77 .70 :7320
,.h,#, #
b.+
50.
35.
a.18 b.6
x:
mo: 78
Solución a cargo del alumno.
34.
a. Con el disco B, e(azul)
-1
b.+
5
45.
a.
a.27
..+
51.
a.72 y 24 b.4O32O c.72
52.
a.24
b.
80 c.270 d.t2
72,
Por eiemplo, fila 7: 2; -3;
AUTOEVATUACIóil
53.
a. Solución a cargo del alumno.
b. Cantidad de materias.
Cuantitativa.
c. Población.
d. Solución a cargo del alumno.
e.7 : 7,36; fiu = 0; fro : 0
f.
34o/o
54.
a. Solución a cargo del alumno.
b.P(suma
=n=2
55,
720
30.
-6;
6;
-6.
a.-6
b.6
a.
b.
c.
c.77
d. -5
f.
9.5
h.0
r. (-5)
3
b. -600 :
MEilTEAITIVA
S0. Operaclones comblnadas
76.
Por ejemplo, a. con 21.
y representac¡ón
t.
Las dos son. incorrectas.
18.
Por ejemplo, fila 1: 5 años a.
79,
a.
2,
C.
3.
Por ejemplo, a.
4.
Solución a cargo del alumno.
5.
a. b, negativoi a y c, positivos.
b. b, positivo; a y c, negativos.
l+8.
6.
Adición y sustracc¡ón
-! d,7
-5 e. 0
c. -2 Í. -2
a.
b.
7.
a.3
b. -8
g.
0
h.2
a. -7
c -2
d.
-6
l. -6
Í,12
8.
Debe depositar $¡OO. -300 + 300
9.
a.x=-3 b.x=1 c.x=3
10.
Por eiemplo, fila 1: -5; 1; -1;
-4;
5.
Solución a cargo del alumno.
ir9. Mutüpllcaclón y divisién
-
-6
c 24
a.
b.0
d, -6
e.0
Í. -40
t6
-
2t.
a.
-500
200
-3
c. -1
f. -300
s -5.
b. Son iguales. d. Son iguales.
a, -4;
b. -5;
-2
-3
d,2; 4
e,30;32
c, -5O7; -499
25.
a. Ninguno. b. Dos.
Por ejemplo, a.
<.
27,
a.-{37; -720; -36; 0;7:34
b, -40; -4; -3:'7; 52;723
c, -75; -72; -2; 0;3;33; 44;
9.72
h. -6
¡. 80
a.
b,
t5,
d,-2
e. -24
f. No es
a.( b.:
b.
posibte.
c.)
4 c,64
-3 d, -796
d.(
e,267
38.
No.
39,
a.74 c.57
b. -22 d, -99
e.-62
f.
18
40.
a.72 c,3
b. 6
d. -30
4t,
a.6
b,4
e. -3
f.
-1
d.0
c.
18
e. -1
Í.5
42.
a,3 c. -90
b.-6 ó.-8y-7
e,5 y 75
AI'TOEVAIUACóII
a,
4.
-2
b.
-300 c 5
-24; -75; 6; 9;
27
Solución a cargo del alumno.
45.
Por ejemplo, fila 1:
-4; -2;3;3.
tt6.
-8
4
c
d.
-6
-3
-74 9.0
Í, -38 h. -4
e,
29.
a. Hay que sumar -o.
b. Hay que restar b.
c
b. No. Puede ser 2 . (-6).
c. No. Et resultado sería positivo.
43,
26.
28.
a.4.(4):a2
37,
a,
5.2
c -8800 m e. -200
d.
t4.
-
3) . 4
Solución a cargo del alumno.
-3
b. El número es -10.
c. Sí, et 0.
36,
2t.
22.
33.
d. -84
740
TIEI{TEAI?IVA
71.
c.
-27 b,14
24.
e. -10
-77
IilTEGRACóil h7.rr8.hs. n
a.
b.
-b
c.
b,
Por eiemplo, a. O2
20,
a,
<.
5
a. 4 cuotas de $130 cada una.
b. 780 - 520 = 260.
a.5
b. -5
c, 6
77.
Por eiemplo, a. -20.
m
a.3.(-3):-e
c. -400
Solución a cargo del alumno.
l+7. Números negativos. Orden
c. No. Le tultan $200.
b.9850
50
t2.
(-2) d. -74
-20 e. (-3)
30 i.43
-600
a.22o
e. -5
t5,
a.
b,77 años.
37,
13.
14.
c. 58 años.
a. 62 años.
No, es positivo.
a.72 c -27
b, -4
d. -32
e. -2
Í.3
47.
Por ejemplo, a. con 14.
4E.
a.75 b. 15 c --72 d. -38
F
{
rl-¡
#
.-r
t-li
-f-l--J -lAdtvft
r .")
I nt
ie'-t}L:1'
.,u
ú
,t
t
t
'frJHI:
[rfl'r',
R¡sporollr.
f. iQué observan en la foto?
2. ácómo les parece que podemos relacionar esta foto con [a matemática?
3. iQuiénes pertenecen a la misma generación?
áCuántas generaciones hay representadas en la foto?
4.
áCuántas personas hay de cada generación distinta a la de Martín? iHay alguna relación entre
estas cantidades?
5.
El grupo formado por los bisabuelos de Martín, icuántas personas lo integran?
6.
Resuelvan.
a. Si pudiéramos reunir en una foto a los padres de Martín, a todos sus abuelos, sus bisabuelos
y sus tatarabuelos, Zcuántas personas habría en ella?
)
b. Escriban un cálculo que les permita encontrar [a cantidad de integrantes de cada nueva generación.
7.
)
)
Lean atentamente
y respondan.
Juan le contó un secreto a su mejor amigo y él pensó lo siguiente: "Como no voy a aguantar más
de 30 minutos sin contárselo a nadie, voy a elegir a dos compañeros para contarles este secreto".
a. Si a su vez, cada uno de estos compañeros le contó el secreto a otros dos a los 30 minutos y en
el curso hay 25 alumnos, ien cuánto tiempo se enteraron todos del secreto de Juan?
b. Si ta misma situación les sucediera a ustedes, ien cuánto tiempo se enteraría todo el curso?
c. iQué suposiciones están haciendo para responder estas preguntas?
t
r*UO,
I
I
\
R¡sponont.
f. iQué observan en la foto?
2. ¿c6mo les parece
que podemos relacionar esta foto con la matemática?
3. tas barritas verticales de metal que tiene et diapasón (mango de la guitarra), áson paralelas
entre sí? áAparecen a la misma distancia una de la otra? zpor qué piensan que es así?
t
4.
Tengan en cuenta [a foto de la guitarn
y resuelvan.
mástit - díapasón
cejuela
traste 4
a. Midan con una regla la longitud de una cuerda entre el puente y la cejuela y marguen en la
foto los puntos que se piden a continuación (tomen la cejuela como 0 y el puente como 1):
¡ La mitad de su longitud. . La tercera parte de su longitud. . La cuarta parte de su longitud.
b. Numeren los casilleros y los trastes comenzando por e[ más cercano a la cejuela. ZCon qué
número de trastes coinciden los puntos que marcaron en el ítem anterior?
c. A cada traste le corresponde un casillero que lleva el mismo número. ZQué parte de [a cuerda
puede vibrar cuando se presiona en los casilleros correspondientes a los trastes marcados?
5.
¡
Lean atentamente y respondan.
En la escala musical hay un total de 12 sonidos (contando las notas y sus sostenidos que se
escriben con #): DO, DO#, RE, RE#, Ml, FA, FA#, SOL, SOL#, LA, LA#, Sl. Después del Sl viene
otra vez DO, y todo recomienza.
Cada cuerda corresponde a una nota diferente. Cuando se apoya e[ dedo sobre un casillero, se
obtiene otra nota y se avanza en la escala según se presionen distintos casilleros.
a. La cuerda de arriba es Ml; si ponemos el dedo en el primer casillero obtenemos FA, en el
segundo FA#, etc. ZQUé nota corresponde al casillero 12? iY al7? LY al
b.
6.
La siguiente cuerda es
lA.
5?
ZQué nota corresponde alcasilleroT2? LY al7? LY al5?
Tengan en cuenta las actividades anter¡ores
y respondan.
La siguiente cuerda produce el sonido DO, pero no tiene los trastes marcados.
PUENTE
CEJUELA
DO
a.
¿En dónde ubicarian el
traste para obtener el siguiente D0? ¿Y para obtener el siguiente
SOL?
Márquenlos en la cuerda.
b. La parte de la cuerda que vibra para obtener DO, Zqué fracción es respecto de la que vibra
para obtener
SOL?
c. Zftiste alguna relación entre las respuestas anteriores y el hecho de que
la respuesta
i
1
: ]i
fxpliquen
I
-j\::
Respot¡ott¡.
1. ¿Qué observan en [a foto?
2.
¿C6mo les parece que podemos relacionar esta foto con [a matemática?
3. A través de [a imagen se pueden descubrir distintas relaciones. Por eiemplo, en algunos
tos hay más compradores que en otros. iA qué se puede deber esta diferencia?
0
,[M
pues-
.^
r
entre el precio de las berenienas y la
cantidad que se vende por día, áen qué momento se venderá más: cuando sube o cuando baia el
precio del kilogramo de bereniena?
4. Por ejemplo, si se tiene en cuenta la relación que existe
5.
Lean atentamente
y resuelvan.
En el barrio donde se tomó [a fotografln viven Estela, Lucio, Héctor y Marisa. Cada uno dijo lo
¡
siguiente sobre e[ precio de [a berenjena:
¡ Estela: "siempre compro 5 kilos de berenjenas, pero si el kilo cuesta $10 o más, no compro nada".
o Lucio: "Si la bereniena cuesta menos de $S el kilo, compro 3 kilos; si cuesta entre $5 y $S (ambos incluidos) compro 1 kilo y si no, no compro".
o Héctor: "siempre compro la cantidad de kilos que me alcance con $10".
o Marisa: "Si e[ precio de la berenjena es $4 o menos, compro 5 kilos; si es mayor que $4 y menor
que $8 compro 4 kitos y si es $8 o más, compro 3 kilos y obviamente no pago más de $12 el kilo".
a. Completen la tabla con las cantidades de berenjenas (en kg), según lo que dijo cada uno.
l
b. Cierto dÍa e[ precio de la berenjena era de $4 et kg y Estela, Lucio,,Héctor y Marisa compraron según lo que comentaron. Si el verdulero pagó e[ kilogramo a $3, icuánto dinero ganó?
)
c
Otro día ofreció las berenjenas a $5 el kg y volvieron a comprar las cuatro personas según lo
que comentaron. Si el verdulero pagó el kilogramo a $3, icuánto dinero ganó?
le conviene vender el kilogramo de berenjenas para obtener la mayor ganancia
posible si paga el kilogramo a $3?
d.
aA qué precio
Rgspo¡onn.
1.
¿Qué obseryan en [a foto? áCómo les parece que podemos relacionarla con
la matemática?
2.
¿Qué figuras forman la superficie de ta pelota? lPor qué piensan que se usa este poliedro
para construir [a pelota y no uno regular?
3.
4.
¿Cuántas figuras de cada tipo ttegan a ver en ta foto? áDe cuáles les parece que hay
más?
Calcuten la cantidad de hexágonos, [a cantidad de aristas
ta tiene en total 12 pentágonos.
y de vértices, si se sabe que ta peto-
o
R¡spo¡or¡.
1. ¿Qué observan en la foto? iCómo les parece que podemos relacionarla con la matemática?
2.
eA qué bola les parece que le va a pegar la chica que está jugando? iEn qué dirección saldrá
la bola si la bola blanca pega en el centro de aquella?
3.
Lean atentamente y respondan.
Cuando se juega sin efecto y se pega a una bola, el ángulo que
forma [a trayectoria de entrada de la bola con la banda es igual al
ángulo de la trayectoria de rebote con la banda.
En el tiro anterior, la bola violeta ientrará en algún agujero?
4- ¿tn qué
dirección debería poner el taco la chica que está jugando, si quiere pegarle a la bola azut?
5. 5i la chica que
estiá iugando quiere pegarle a la bola 15 haciendo una banda, icómo puede
hacer? iEntrará en algún
6-
En el
7.
Lean atentamente
lado?
:
tiro anterior, áde qué tado habrÍa que pegarte a la bola 15 para que haya más chances
de que entre en el hoyo del fondo a la derecha?
y respondan.
Las marquitas que están en e[ borde de [a mesa dividen el ancho de esta en 4 partes iguales y et
largo, en 8. Sirven para poder medir los ángulos de entrada y satida de las bolas aI hacer banda.
En la imagen se ven las líneas imaginarias que pueden s"r¡t de guía para calcular las trayector¡as
y un ejemplo en e[ que [a bola 1 entra en el agujero de coordenadas (8;0) si hace banda en (6;4).
a
iDónde tendria que hacer banda [a bola
2 para que entre en el agujero de coordenadas (0;O)?
b. iDónde tendría que hacer banda la bola 3 para que entre en el agujero de coordenadas (4;4)?
c
&
ZDónde tendr'r,a que hacer banda la bola
4
para que entre en el agujero de coordenadas (4;4)?
Trabaien con un compañero. Dibujen en una hoja cuadriculada un rectángulo como el det ejercicio anterior con algunas bolas. Propongan distintas jugadas para que las botas entren en los
agujeros. Recuerden escribir las coordenadas.
r
r
J
Respor,¡onn.
1. ¿Qué observan en [a foto? áCómo les parece que podemos retacionarla con [a matemática?
2.
Las mesas áson todas iguales? áCómo se podrían clasificar según su forma? iQué otros tipos
de mesas conocen?
3.
Foco, Fran, Santi, Seba, Lucas y Pablo quieren cenar en este restaurante.
a. ZQué tipo de mesa les puede ofrecer eI mozb para sentarse? iQué opción les conviene elegir?
b. Si etigen la mesa circutar y piden una porción de papas fritas de entrada, Zdónde tienen que
ubicar e[ ptato para que esté a[ alcance de todos?
c. Si et mozo les prepara dos mesas cuadradas juntas, Zdónde debería ubicar el plato de papas fritas?
4.
¿Qué otra forma podría tener una mesa para 6 personas que permita ubicar et ptato de papas
fritas para que esté a[ atcance de todos?
R¡sporolrr.
1. ¿Qué observan en [a foto? áCómo les parece que podemos relacionarla con [a matemática?
2.
Resuelvan.
observen e[ sector del estacionamiento que se encuentra al lado del edificio
de techos negros.
a. Si un auto mide en promedio entre 4 y 5 metros de largo, y entre 1.,6y 2 metros
de ancho,
icuál es el perímetro de ese sector? Zy su
área?
b. Si una persona quiere dar una vuelta completa al edificio de techos negros (caminando
cerca
de la pared), icuántos metros recorrerá aproximadamente?
c ZQué área ocupa aproximadamente ese edificio?
o
'%.
rrl
f'-
J
-r#r,)r0Ntrs
\
lú;)
'
.¡d-.
.l
h,
l;r.'
l.l
i
N'iff
RrspoHo¡r.
1. áQue observan en [a foto?
2. iC6mo les parece
que se puede retacionar esta foto con [a matemática?
3. i,Cómo se puede hacer e[ recuento de votos para que sea
1o
más rápido posible?
4'
Antes de la votación' se encuestó a 30 de los 500 alumnos que
concurren a la escuela para
saber a quién iban a votar como'presidente. iEs representativa
la información que se pudo haber
conseguido?
5' ¿y s¡ se tuviera los datos de un curso de 40 atumnos? isená [o mismo
si se elige a
de distintos cursos?
ft
alumnos
6' Reúnanse en gruPos y realicen una encuesta en el curso para obtener los siguientes
datos:
sexo, altura, talle de calzado, color de pelo. luego, resuelvan.
a' Representen en el pizarrÓn los datos que obtuvieron usando algún recurso que
sirva para
analizarlos.
b. iCuát es [a altura que más veces se repite?
c. iCuát es e[ talle de calzado que más veces se repite?
d.
ZCuát es
el color de pelo que más veces se repite?
e'
ZHay alguna relación entre el sexo y la altura? ZY entre
la altura y e[ color de pelo?
altura y el talle de calzado? Expliquen las respuestas.
' A paftir de tos datos que obtuvieron en la encuesta
ise puede asegurar gue es [a misma en todo et país?
7
iy
entre la
sobre la altura que más veces se repite,
t
r
Respotromr.
1. áQué observan en [a foto? iCómo les parece que podemos relacionarla con [a matemática?
2. Si et buzo que se encuentra más cerca de [a superfcie está situado 20 metros baio et nivel del mar,
áa qué profundidad se encuentran sus compañeros? iQué cosas tuvieron en cuenta para responder?
3. iQué pasaría si todos
4.
ascienden 5 metros? áQué cálcuto hicieron?
Dos metros más abajo del buzo que se encuentra a mayor profundidad comienza la formación
de coral, que tiene 12 metros de altura desde e[ fondo del mar. iQué profundidad tiene e[ mar en
esa zona?
5. Si a 20 m sobre [a supefficie del mar pasa un helicóptero que envía una señal sonoft¡ para calcular
la profundidad del mar, icuántos metros recore la onda sonon hasta chocar con e[ fondo?
Ad'NÑ
Fil
I
C
t)
]GRIJPO
]MACMILLAN
N-Nn@
l
ffi
MATEMATICA
rEé1,***l
| :.1 con l¡bros,
I
I
I
no con fotocopias
Pupnro DEPrros