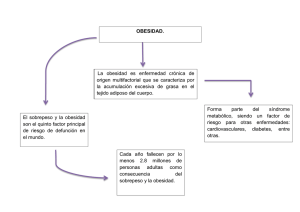
Universidad Autónoma de Yucatán Facultad de matemáticas Licenciatura en Actuaría Estadística No Paramétrica Profesor: M. en C. Salvador Medina Peralta ADA 4 Unidad 4 Equipo 5: Cauich Loria Dianelly Yireth Lope Estrella Jesús Daniel Pinto Itzá Neidy Fabiola Fecha de entrega: 30 de octubre de 2023 Prueba exacta de Fisher (Para una tabla de contingencia) La prueba de probabilidad exacta de Fisher para tablas de 2x2 es una herramienta empleada para analizar datos discretos cuando se tienen dos muestras independientes con tamaños pequeños. Se utiliza cuando se desean comparar dos puntuaciones pertenecientes a dos grupos distintos que caen en una de dos categorías mutuamente excluyentes. Es decir, la prueba de Fisher se emplea para determinar si existe una asociación significativa entre dos o más variables cualitativas cuando la muestra es demasiado pequeña y no se pueden cumplir los supuestos necesarios para utilizar la prueba chi-cuadrado. Estas variables se presentan en forma de frecuencias en una tabla de contingencia de 2x2, como se muestra en la Tabla 1. Es importante destacar que la prueba de Fisher puede aplicarse a tablas de mayor tamaño, es decir, de m x n, siempre que m y n sean mayores o iguales a 2. No obstante, en este contexto específico, se enfoca en tablas de contingencia de 2x2. Tabla 1. Tabla de contingencia de 2 × 2. Grupo Variable I II Combinación + a b a+b c d c+d Total a+c b+d n La prueba evalúa si hay una diferencia significativa en las proporciones de signos positivos y negativos entre los grupos I y II, tal como se refleja en los valores de a, b, c y d en la Tabla 1. En otras palabras, se busca determinar si hay una disparidad estadísticamente relevante en la distribución de signos más (+) y menos (-) en ambos grupos. Ejemplos 1. [Fuente: Pértega, S. Pita, S. (2004), ejemplo 1] En una determinada población se desea averiguar si existen diferencias en la prevalencia de obesidad entre hombres y mujeres o si, por el contrario, el porcentaje de obesos no varía entre sexos. Tras ser observada una muestra de 14 sujetos se obtuvieron los resultados que se muestran en la Tabla 1.1. Tabla 1.1. Tabla de contingencia para estudiar las diferencias en la prevalencia de obesidad entre sexos. Estudio de prevalencia sobre 14 sujetos. Obesidad Sexo Sí No Total Mujeres Hombres Total 1 (a) 7 (c) 8 (a+c) 4 (b) 2 (d) 6 (b+d) 5 (a+b) 9 (c+d) 14 (n) Supuestos Según Daniel (1990), la prueba exacta de Fisher, que también se denomina prueba de Fisher-Irwin, fue descrita simultáneamente por Fisher (1934, 1935), Irwin (1935) y Yates (1934). Por lo que comparten los mismos supuestos para la prueba de ji-cuadrado para tablas 𝑟 × 𝑐 con la excepción del supuesto relativo a las frecuencias esperadas pequeñas (que refleja las limitaciones de esta última prueba con tamaños de muestra pequeños). - Se tienen 𝑘 muestras independientes. Escala de medición nominal u ordinal. Los dos grupos de la variable categórica son mutuamente excluyentes (cada observación contribuye únicamente a uno de los niveles). Las frecuencias marginales de las columnas y las filas son fijas. Hipótesis Coloquialmente: 𝐻0 : La proporción de observaciones en la fila 1 que cae en la celda a es igual a la proporción de observaciones en la fila 2 que cae en la celda c. 𝐻1 : La proporción de observaciones de la fila 1 que cae en la celda a no es igual a la proporción de observaciones en la fila 2 que cae en la celda c. Formalmente: 𝐻0 : 𝜋1 = 𝜋2 𝑣𝑠 𝐻1 : 𝜋1 ≠ 𝜋2 Estadística de prueba Se sabe que la distribución chi-cuadrado proporciona una aproximación a la distribución muestral exacta para una tabla de contingencia. En el caso de tablas de 2 × 2, la distribución chi-cuadrado se emplea para aproximar la distribución hipergeométrica. La ecuación para una variable con distribución hipergeométrica, permite el cálculo de la probabilidad exacta (P) de obtener un conjunto específico de frecuencias observadas en una tabla de contingencia 2 × 2. Por lo que el estadístico de prueba es: 𝑎+𝑐 𝑏+𝑑 ( )( ) 𝑎 𝑏 𝑃= 𝑛 ( ) 𝑎+𝑏 Esto es equivalente a = (𝑎 + 𝑐)! (𝑏 + 𝑑)! (𝑎 + 𝑏)! (𝑐 + 𝑑)! 𝑛! 𝑎! 𝑏! 𝑐! 𝑑! Cálculo del valor P Dada la ecuación 𝑃= (𝑎 + 𝑐)! (𝑏 + 𝑑)! (𝑎 + 𝑏)! (𝑐 + 𝑑)! 𝑛! 𝑎! 𝑏! 𝑐! 𝑑! genera el mismo valor p que la distribución hipergeométrica con los siguientes parámetros: 𝑛 = tamaño de la población 𝑎 + 𝑏 = “éxitos” de la población 𝑎 + 𝑐 = tamaño de muestra 𝑎 = muestra de “éxitos” Región de rechazo A diferencia de algunas pruebas de hipótesis paramétricas, como la prueba t o la prueba F, la prueba exacta de Fisher no se basa en una región de rechazo específica. En su lugar, calcula la probabilidad de observar los resultados observados, o resultados más extremos, bajo la hipótesis nula de independencia entre las variables categóricas. Si esta probabilidad es lo suficientemente baja, generalmente por debajo de un nivel de significancia previamente definido (como 0.05), se rechaza la hipótesis nula, lo que sugiere que hay una asociación significativa entre las variables. Ejemplos 1. [Fuente: Pértega, S. Pita, S. (2004), ejemplo 1] En una determinada población se desea averiguar si existen diferencias en la prevalencia de obesidad entre hombres y mujeres o si, por el contrario, el porcentaje de obesos no varía entre sexos. Tras ser observada una muestra de 14 sujetos se obtuvieron los resultados que se muestran en la Tabla 1.1. Tabla 1.1. Tabla de contingencia para estudiar las diferencias en la prevalencia de obesidad entre sexos. Estudio de prevalencia sobre 14 sujetos. Obesidad Sexo Sí No Total Mujeres Hombres Total 1 (a) 7 (c) 8 (a+c) 4 (b) 2 (d) 6 (b+d) 5 (a+b) 9 (c+d) 14 (n) Solución Identificación de elementos *Unidad experimental: Personas que se les pregunto si tienen obesidad o no (14 sujetos). *Variable respuesta: Hay dos variables de respuesta en este contexto - Padecimiento (Sí tiene obesidad, No tiene obesidad). -Sexo (Mujeres, Hombres). *Escala de medición de las variables: Escala nominal. *Parámetros involucrados en el contexto del problema: La proporción de sujetos mujeres que sí tienen obesidad (𝜋1 ) y la proporción de sujetos hombres que sí tienen obesidad (𝜋2 ). *Verificación de supuestos: 1.- Las muestras son independientes, la muestra de mujeres con obesidad y sin obesidad es independientes a la muestra de hombres con obesidad y sin obesidad. 2.- Escala de medición nominal. 3.- Los dos grupos de la variable categórica (Con obesidad y sin obesidad) son mutuamente excluyentes (cada observación contribuye únicamente a uno de los niveles). 4.- Las frecuencias marginales de las columnas y las filas son fijas. Hipótesis Coloquialmente: 𝐻0 : La proporción de sujetos mujeres que sí tienen obesidad es mayor o igual a la proporción de sujetos hombres que sí tienen obesidad. 𝐻1 : La proporción de sujetos mujeres que sí tienen obesidad es menor a la proporción de sujetos hombres que sí tienen obesidad Formalmente: 𝐻0 : 𝜋1 ≥ 𝜋2 𝑣𝑠 𝐻1 : 𝜋1 < 𝜋2 Estadístico de prueba 𝑎+𝑐 𝑏+𝑑 ( )( ) 𝑎 𝑏 𝑃= 𝑛 ( ) 𝑎+𝑏 O su equivalente 𝑃= (𝑎 + 𝑐)! (𝑏 + 𝑑)! (𝑎 + 𝑏)! (𝑐 + 𝑑)! 𝑛! 𝑎! 𝑏! 𝑐! 𝑑! donde 𝑛 = tamaño de la población 𝑎 + 𝑏 = “éxitos” de la población 𝑎 + 𝑐 = tamaño de muestra 𝑎 = muestra de “éxitos” Cálculo del estadístico de prueba 1+7 4+2 8 6 ( )( ) ( ) ( ) (8)(15) 120 1 4 𝑃= = 1 4 = = = 0.059940059 14 14 (2002) 2002 ( ) ( ) 1+4 5 = (8)! (6)! (5)! (9)! 1,264,146,186,000,000 = = 0.059940059 14! 1! 4! 7! 2! 21,090,172,210,000,000 Valor P El valor p es eta dado por el mismo estadístico de prueba. 𝑃= (𝑎 + 𝑐)! (𝑏 + 𝑑)! (𝑎 + 𝑏)! (𝑐 + 𝑑)! (8)! (6)! (5)! (9)! 1,264,146,186,000,000 = = 𝑛! 𝑎! 𝑏! 𝑐! 𝑑! 14! 1! 4! 7! 2! 21,090,172,210,000,000 = 0.059940059 Ahora, se debe identificar las desviaciones más extremas de la distribución supuesta por 𝐻0 que podrían ocurrir con los mismos totales marginales, y se debe tener en cuenta esas posibles desviaciones extremas, para el establecimiento de la hipótesis nula. Se analiza cuál es la probabilidad cuando 𝐻0 es verdadera, de la ocurrencia de las posibles combinaciones de frecuencias que se podrían obtener con los mismos totales marginales . Dada por la Tabla 1.2: Tabla 1.2. Posibles combinaciones de frecuencias con los mismos totales marginales (i) (ii) (iii) Obesidad Obesidad Si No Si No Mujeres 0 5 5 Mujeres 3 2 5 Hombres 8 1 9 Hombres 5 4 9 8 6 14 8 6 14 Mujeres 1 4 5 Mujeres 4 1 5 Hombres 7 2 9 Hombres 4 5 9 8 6 14 8 6 14 Mujeres 2 3 5 Mujeres 5 0 5 Hombres 6 3 9 Hombres 3 6 9 8 6 14 8 6 14 (iv) (v) (vi) Se calcula P para cada caso, usando la misma ecuación, de manera que se obtiene la tabla 1.3. Tabla 1.3. Probabilidad exacta asociada con cada una de las disposiciones de frecuencias. a b c d p (i) 0 5 8 1 0,0030 (ii) 1 4 7 2 0,0599 (iii) 2 3 6 3 0,2797 (iv) 3 2 5 4 0,4196 (v) 4 1 4 5 0,2098 (vi) 5 0 3 6 0,0280 El valor de la p asociado al test exacto de Fisher puede entonces calcularse sumando las probabilidades de las tablas que resultan ser menores o iguales a la probabilidad de la Tabla 1.1 (𝑃 = 0.0599) que ha sido observada: 𝑃 = 0.0599 + 0.0030 + 0.0280 𝑃 = 0.0909 Decisión con 𝜶 = 𝟎. 𝟎𝟓, utilizando el valo-p Como 𝑃 = 0.0909 > 0.05, no se rechaza 𝐻0 y se puede concluir con un nivel de significancia del 5% que existe evidencia estadísticamente significativa para decir que la proporción de sujetos mujeres que sí tienen obesidad es mayor o igual a la proporción de sujetos hombres que sí tienen obesidad. Por lo tanto, los datos indican que el padecimiento de obesidad no está influenciado por el sexo. Resultado en R Medida de asociación (Odds e intervalo de confianza) El Odds Ratio es una medida ampliamente utilizada en epidemiología, particularmente en estudios de casos y controles. Representa la relación entre la probabilidad de que un evento ocurra en comparación con la probabilidad de que no ocurra. En términos sencillos, el Odds Ratio es el cociente entre dos Odds. En estudios de casos y controles, el Odds Ratio compara la probabilidad de estar expuesto a un factor de riesgo en el grupo de casos (personas con la enfermedad o condición en estudio) con la probabilidad de estar expuesto al mismo factor de riesgo en el grupo de control (personas sin la enfermedad o condición). Básicamente, nos permite entender si la exposición a un factor en particular está asociada con un mayor riesgo de desarrollar la enfermedad en cuestión. Un Odds Ratio mayor a 1 indica un mayor riesgo asociado, mientras que un Odds Ratio menor a 1 indica un menor riesgo. Formula Expuestos No expuestos Casos A C Controles b d 𝑎 (𝑎)(𝑑) 𝑜𝑑𝑑𝑠 𝑑𝑒 𝑒𝑥𝑝𝑜𝑠𝑖𝑐𝑖ó𝑛 𝑒𝑛 𝑐𝑎𝑠𝑜𝑠 𝑂𝑅 = = 𝑐 = 𝑜𝑑𝑑𝑠 𝑑𝑒 𝑒𝑥𝑝𝑜𝑠𝑖𝑐𝑖ó𝑛 𝑒𝑛 𝑐𝑜𝑛𝑡𝑟𝑜𝑙𝑒𝑠 𝑏 (𝑐)(𝑏) 𝑑 Intervalo de confianza Exactamente, el Odds Ratio es una medida que ayuda a entender la asociación entre un factor y una enfermedad, pero como cualquier estimación, tiene un grado de incertidumbre. El intervalo de confianza (IC) es una herramienta estadística que proporciona un rango dentro del cual es probable que se encuentre el valor real del Odds Ratio. Esto es especialmente útil cuando se está tratando de evaluar la fuerza de la asociación. Cuando el Odds Ratio se acerca a 1, significa que el factor de riesgo no está fuertemente asociado con la enfermedad, y el IC generalmente será más estrecho, lo que indica mayor precisión. Sin embargo, cuando el Odds Ratio es significativamente mayor o menor que 1, la estimación puede ser menos precisa, y el IC se vuelve más amplio, reflejando la mayor incertidumbre. En otras palabras, el IC nos dice cuán seguros podemos estar de la estimación del Odds Ratio, y un IC más estrecho indica una estimación más precisa. En resumen, el intervalo de confianza del Odds Ratio nos proporciona una medida de la incertidumbre alrededor de la asociación entre un factor y una enfermedad, lo que es esencial para interpretar adecuadamente los resultados de un estudio epidemiológico. Formula 𝐼𝐶 = 𝑂𝑅 Donde 𝑶𝑹 es Odds Ratio 𝑍 (1± ) 𝑋ℎ𝑚 𝒁 constante dependiente del porcentaje (Por ejemplo: 95% = 1.96) 𝑿𝒉𝒎 es el chi cuadrado de 𝐻𝑀 (𝑛 − 1)(𝑎 ∙ 𝑑 − 𝑏 ∙ 𝑐)2 𝑋ℎ𝑚 = √ (𝑎 + 𝑏)(𝑐 + 𝑑)(𝑎 + 𝑐)(𝑏 + 𝑑) Usos: Permite reconocer la naturaleza como factor de riesgo o de protección de una exposición Permite identificar la magnitud o fuerza de asociación, lo que permite hacer comparaciones Es de gran utilidad en los estudios de casos y controles Si el resultado de Odds Ratio es mayor a 1 la asociación es positiva, es decir que la presencia del factor se asocia a la mayor ocurrencia del evento. Se le considera un Factor de Riesgo. Si el resultado de Odds Ratio es menor a 1 la asociación es negativa, es decir que la presencia del factor no se asocia con la mayor ocurrencia del evento. Se le considera un Factor de Protección. Si el resultado de Odds Ratio es igual a 1 no hay asociación entre las variables, es decir que la cantidad de veces que el evento ocurra va a ser igual con o sin la presencia del factor, la relación es 1:1. El Odds Ratio puede ser traducido a probabilidades, mediante la siguiente formula: 𝑃= 𝑂𝑅 1 + 𝑂𝑅 Por ejemplo, si el OR es 0.4 interpretaríamos como que es 0.4 veces más probable que un evento este asociado a la presencia de un factor, al traducirlo a probabilidad se obtiene 0.286 o lo que es igual a 28.6% en este caso la interpretación seria que existe un 28.6% de probabilidad de que un evento este asociado a la presencia de un factor. Los resultados del Intervalo de Confianza permiten establecer si una asociación es estadísticamente significativa. Cuando el resultado incluye el 1 podemos decir que la asociación encontrada no es estadísticamente significativa y si no incluye el 1 la asociación es estadísticamente significativa Ejemplo 2. [Fuente: Cerda, J, Vera, C, Rada, G. (2013), ejemplo 1] Se evaluó la asociación entre el antecedente de migraña y el desarrollo de síndrome hipertensivo del embarazo (SHE) utilizando un estudio de cohorte. Para ello siguieron a 685 embarazadas normotensas entre 11 y 16 semanas de gestación, 264 con antecedente de migraña y 421 sin este antecedente. En el grupo de embarazadas con antecedente de migraña 24 desarrollaron SHE y 240 no lo hicieron; por su parte, en el grupo de embarazadas sin antecedente de migraña 13 desarrollaron SHE y 408 no lo hicieron. Estime un intervalo de confianza del 95%. Solución Identificación de elementos *Unidad experimental: Mujeres embarazadas de entre 11 y 16 semanas de gestación. *Variable de respuesta en el contexto del problema: Se tiene dos variables de respuesta en este caso: 1. Síndrome hipertensivo del embarazo. 2. Antecedentes de migraña. *Escala de medición de las variables involucradas: Escala nominal. *Parámetro(s) involucrado(s) en el contexto del problema: 𝑂𝑅. *Verificación de supuestos: (264)(37) 𝐸[𝑛11 ] = = 14.2598 685 (264)(648) 𝐸[𝑛12 ] = = 249.7401 685 (421)(37) 𝐸[𝑛21 ] = = 22.7401 685 (421)(648) 𝐸[𝑛22 ] = = 398.2598 685 Se confirma que las frecuencias esperadas 𝐸[𝑛𝑖𝑗 ] son mayores que 1 y ninguna es menor que 5. Calculo del valor de 𝑶𝑹 Exposición: Antecedente de migraña Sí No Total Evento de interés: Síndrome hipertensivo del embarazo (SHE) Ocurre No ocurre 𝑎 = 24 𝑏 = 240 𝑐 = 13 𝑑 = 408 𝑎 + 𝑐 = 37 𝑏 + 𝑑 = 648 𝑂𝑅 = (𝑎)(𝑑) (24)(408) 9792 = = = 3.1384 (𝑐)(𝑏) (13)(240) 3129 Total 𝑎 + 𝑏 =264 𝑐 + 𝑑 =421 𝑛 = 685 Además el valor de chi cuadrado de 𝐻, está dado por: (𝑛 − 1)(𝑎 ∙ 𝑑 − 𝑏 ∙ 𝑐)2 (684)(9792 − 3129)2 𝑋ℎ𝑚 = √ =√ = 3.3757 (𝑎 + 𝑏)(𝑐 + 𝑑)(𝑎 + 𝑐)(𝑏 + 𝑑) (264)(421)(37)(648) Calcular el valor 𝒁 con un 95% de confianza. 𝑍 = 1.96 Calcular los límites del intervalo de confianza. 𝐼𝐶 = 𝑂𝑅 𝑍 (1± ) 𝑋ℎ𝑚 Límite inferior: 1.96 (1− ) 3.3757 = 1.3161 1.96 (1+ ) 3.3757 = 4.9606 𝐼𝐶 = (3.1384) Límite superior: 𝐼𝐶 = (3.1384) Por lo que el intervalo de confianza es [1.3161, 4.9606] En probabilidades 𝑃= 𝑂𝑅 3.1384 = = 0.7583 1 + 𝑂𝑅 1 + 3.1384 Los límites del intervalo de confianza para el 95% para un 𝑂𝑅 de 3.1384 están entre 1.3161 y 4.9606, lo que significa que no se trata de una asociación estadísticamente significativa de protección. Es 3.1384 veces más probable que la posibilidad de padecer síndrome hipertensivo del embarazo (SHE) no este asociado a los antecedentes de migraña. Otra interpretación es: existe un 75.83% de probabilidad de que la posibilidad de padecer síndrome hipertensivo del embarazo (SHE), no este asociado a los antecedentes de migraña. Resultado en R Referencias Kvam, P. &. (2007). En Nonparametric Statistics with Applications to Science and Engineering (pág. 163). New Jersey: NU: Willey. Sheskin, D. J. (2000). En D. J. Sheskin, Handbook of Parametric and Nonparametric Statistical Procedures (pág. 390). Florida: FL: Chapman & Hall. Siegel, S. y. (2007). En Estadística no paramétrica: aplicada a las ciencias de la conducta (pág. 129). México: Trilla, 4a. ed. Pértega, S, Pita, S (2004). Asociación de variables cualitativas: El test exacto de Fisher y el test de Mcnemar. Recuperado de: https://www.fisterra.com/formacion/metodologiainvestigacion/asociacion-variables-cualitativas-test-exacto-fisher-test-mcnemar/#sec5 Cerda, J, Vera, C, Rada, G. (2013). Odds ratio: aspectos teóricos y prácticos. Reviste medica de chile. Recuperado de: https://www.scielo.cl/scielo.php?script=sci_arttext&pid=S0034-98872013001000014