Matriz de rotación en geogebra

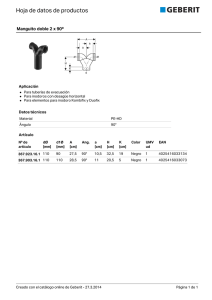
Rotación de curvas en geogebra
”Geogebra Animado”
No olvides comentar y suscribirte al canal
Matrı́z de rotación:
R(θ) =
cosθ −senθ
senθ cosθ
Transformación lineal asociada:
cosθ −senθ
x
T [R(θ)] =
senθ cosθ
y
T (x, y) = (xcosθ − ysenθ, xsenθ + ycosθ)
Sea V una función vectorial V : R −→ R2 definida por V (t) = (x(t), y(t)),
formando la composición T ◦ V : R −→ R2 :
T [V (t)] = (x(t)cosθ − y(t)senθ, x(t)senθ + y(t)cosθ)
T ◦ V representa las imágenes de la función V rotadas un ángulo fijo θ , para
algún 0 ≤ θ ≤ 2π.
1
Ejemplo 1: Rotación de una elipse ξ con centro en el origen.
Sea ξ :
x2 y 2
+ 2 = 1 una elipse tal que a 6= b y a, b > 0
a2
b
A continuación se encontrarán unas ecuaciones parámetricas para ξ como
sigue:
x 2 y 2
x2 y 2
+
=1
+ 2 = 1 −→
a2
b
a
b
x
y
haciendo cos(t) = , y, sen(t) = , cos2 (t) + sen2 (t) = 1, ası́, las ecuaciones
a
b
paramétricas para ξ vienen dadas por:
(
x(t) = a · cos(t)
, 0 ≤ t ≤ 2π
y(t) = b · sen(t)
generando la función vectorial V (t) = (x(t), y(t)) (el lector debe probar que
efectivamente V (t) es una función), haciendo la composición T [V (t)]:
T [V (t)] = (x(t)cosθ − y(t)senθ, x(t)senθ + y(t)cosθ)
sustituyendo x(t) = acos(t) , y, y(t) = bsen(t) en T [V (t)] , se obtiene:
T [V (t)] = (acos(t)cosθ − bsen(t)senθ, acos(t)senθ + bsen(t)cosθ)
T [V (t)] es la elipse ξ rotada un ángulo fijo θ , con, 0 ≤ θ ≤ 2π
2
Ensamble con Geogebra 6
A continuación se mostrará el ejemplo 1 en Geogebra 6, para esta ejemplificación se utilizarán deslizadores y el comando curva.
Comando curva:
Curva(< Expresión >, < Expresión >, < P arámetro >, < V alor inicial >, < V alor f inal >)
Si se toman las ecuaciones paramétricas
(
x(t) = 3 · cos(t)
y(t) = 2 · sen(t)
, 0 ≤ t ≤ 2π
en la sentencia del comando curva, hay dos espacios que dicen < Expresión >,
cada uno de esos espacios se llenan con x(t) y y(t), esto es,
Curva(3cos(t), 2sen(t), < P arámetro >, < V alor inicial >, < V alor f inal >)
en parámetro va a ir la letra con que se quiera asignar el parámetro, en este
caso ”t”, quedando de la siguiente forma:
Curva(3cos(t), 2sen(t), t, < V alor inicial >, < V alor f inal >)
los espacios < V alor inicial > y < V alor f inal >, se llenarán con los valores
entre los cuales varı́a el parámetro ”t”, esto es, 0 y 2π, quedando construida
la sentencia de la siguiente forma:
Curva(3cos(t), 2sen(t), t, 0, 2π)
3
en la siguiente figura se muestra la gráfica obtenida:
Figura 1:
Ahora, ya sabiendo los parámetros de la sentencia ”curva”, se mostrará la
construcción paso a paso de una animación que rote cualquier ángulo dado,
una elipse cualquiera con centro en el origen.
Paso 1: Creación de los deslizadores necesarios
Son necesarios tres deslizadores, uno que va a variar el ángulo de rotación,
y dos deslizadores numéricos a y b no nulos, que van a variar en la función
V (t) = (acos(t), bsen(t)).
Deslizador angular:
Primero que todo debe dirigirse a la barra de herramientas y dar click en
deslizador, al realizar esta acción, se abre un cuadro de diálogo como el que
se muestra en al siguiente figura:
4
Figura 2:
Se selecciona la opción ángulo y se asigna un nombre a este; la configuración
se realiza acorde con las condiciones del ejemplo 1, θ es un ángulo positivo
entre 0 y 2π, para el caso de geogebra 6, se declarará el recorrido del ángulo
en el sistema sexagesimal, el mı́nimo se establecerá en 0◦ y el máximo en
360◦ , y, el aumento del deslizador en 0,1◦ , naturalmente, el aumento es de la
escogencia adecuada del usuario.
5
Deslizadores numéricos:
Debe dirigirse a la barra de herramientas y dar click en deslizador, al realizar
esta acción, se abre un cuadro de diálogo como el que se muestra en la
siguiente figura:
Figura 3:
Se selecciona la opción número y se asigna un nombre a este, en este caso a al
primer deslizador numérico, y b al segundo, en el ejemplo 1, se establecieron
las condiciones a 6= b y a, b > 0, por tanto, en la imagen anterior el deslizador
comienza en 0,1, naturalmente puede empezar según la escogencia del usuario, además, cabe resaltar que si a = b, la elipse se torna una circunferencia y
la rotación expuesta carecerı́a de sentido, además, a y b son reales positivos
ya que, en la construcción de la elipse, estos son distancias.
Botones asociados a la animación de los deslizadores:
Con el fin de facilitar la animación de un deslizador en Geogebra 6, resulta
conveniente usar la herramienta botón ubicada en la barra de herramientas,
en este ejemplo 1, solo se animará el deslizador correspondiente al ángulo fijo
θ de la matriz de rotación, y se utilizarán los siguientes cuatro botones:
6
”P lay”, ”P ause”, ”Stop”, ”Centrar V ista”
P lay: al dar click en este botón, la animación del deslizador asociado empieza.
Cuando se da click en al herramienta botón y luego se da click sobre la vista
gráfica, se abre un cuadro de diálogo en el cual se va a configurar la animación
del deslizador ”ang”, en la sección ”Guión (script) de GeoGebra”, en donde
se escribirá la siguiente sentencia incluyendo acentos ”tíldes ”:
IniciaAnimación[ang, true]
”ang” hace referencia al nombre del deslizador angular, y ”true” al valor
de verdad, a continuación se expone una imagen que muestra la situación
planteada:
Figura 4:
P ause: al dar click en este botón, la animación del deslizador asociado se
detiene en el valor en el que se encuentre.
Para la programación del botón ”P ause”, se siguen los mismos pasos de
creación del botón ”P lay” pero con la siguiente sentencia:
IniciaAnimación[ang, f alse]
7
”ang” hace referencia al nombre del deslizador angular, y ”f alse” al valor
de verdad, a continuación se expone una imagen que muestra la situación
planteada:
Figura 5:
Stop: al dar click en este botón, la animación del deslizador asociado se detiene y además regresa el deslizador a su valor inicial.
La creación del botón ”Stop” lleva la siguiente sentencia:
IniciaAnimación[ang, f alse]
ang = 0◦
”ang” hace referencia al nombre del deslizador angular, ”f alse” al valor de
verdad, y ang = 0◦ reinicia el deslizador a cero grados, a continuación se
expone una imagen que muestra la situación planteada:
8
Figura 6:
Centrar vista: al dar click en este botón, el origen de la vista gráfica [punto
(0, 0)] se desplaza al centro de la pantalla
La creación del botón ”Centrar vista” lleva la siguiente sentencia:
V istaCentrada[(0, 0)]
”(0, 0)” hace referencia al origen que es el punto que se va a desplazar al
centro de la pantalla, a continuación se expone una imagen que muestra la
situación planteada:
9
Figura 7:
Perzonalización de botones (Opcional): para establecer un entonrno gráfico
más agradable, es posible personalizar los botones poniendo una imagen en
este para esto, se da click derecho encima del botón, se abre un menú desplegable y luego entrar a configuración, después en la pestaña estilo hay un
recuadro que dice ”Elegir desde archivo”, al dar click se abre un nuevo recuadro ”Seleccionar archivo”, en donde se seleccionará la imagen de tamaños
adecuados que se desee poner en el botón. La siguiente imagen muestra la
configuración del archivo con los botones personalizados.
10
Figura 8:
Descargar Botones Personalizados
Paso 2: definición de las funciones seno y coseno
Después de creados los deslizadores, en la barra de entrada se escriben la
siguientes sentencias: f (x) = acos(x) , y luego, g(x) = bsen(t)
cabe recordar que f y g vienen de una previa parametrización de la elipse ξ.
11
Figura 9:
Recuerde ocultar las gráficas de las funciones f y g.
Paso 3: definición de la rotación
La composición T ◦ V definida en el ejemplo 1, generaba la rotación de las
imágenes de la función V un ángulo fijo θ, ahora, con la ayuda de la sentencia
”Curva”se va a graficar la elipse y además se va a rotar; con anterioridad
se definió T [V (t)] = (x(t)cosθ − y(t)senθ, x(t)senθ + y(t)cosθ), esta función
vectorial se puede escribir en la barra de entrada de Geogebra 6 como:
h(t) = (f (t) ∗ cos(ang) − g(t) ∗ sen(ang), f (t) ∗ sen(ang) + g(t) ∗ cos(ang))
nótese que en esa definición no se está restringiendo el parámetro t, por tanto,
es necesario plantear una sentencia condicional que especifique la restricción
de parámetro como sigue:
Si[0 ≤ t ≤ 2π, h(t) = f (t) ∗ cos(ang) − g(t) ∗ sen(ang), f (t) ∗ sen(ang) + g(t) ∗ cos(ang)]
con el fin de evitar la sentencia condicional ”Si”, se recurrirá a la sentencia
”Curva”, cuya estructura es algo más simple, tal y como se habı́a expuesto
con anterioridad, ası́ que la sentencia que genera la rotación de la imágenes
de la función vectorial asociada a la elipse ξ esta dada por:
Curva(f (t) ∗ cos(ang) − g(t) ∗ sen(ang), f (t) ∗ sen(ang) + g(t) ∗ cos(ang), t, 0, 2π)
12
la siguiente imágen muestra el resultado final de la construcción de la rotación de la elipse ξ, naturalmente, con modificaciones de color y grosor del
trazo.
Figura 10:
(QPDQX
HO
)UDQFLVF
R&DVWUR
*XHUUHUR
13
)LUPDGRGLJLWDOPHQWH
SRU(QPDQXHO)UDQFLVFR
&DVWUR*XHUUHUR
'1FQ (QPDQXHO
)UDQFLVFR&DVWUR*XHUUHUR
JQ (QPDQXHO)UDQFLVFR
&DVWUR*XHUUHUR
F &RORPELDO &2
H SDFKROVOP#JPDLOFRP
0RWLYR6R\HODXWRUGHHVWH
GRFXPHQWR
8ELFDFLyQ%RJRWi
&RORPELD
)HFKD