matlab 1

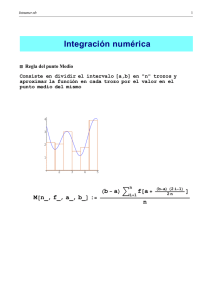
a)
X = [0, 0.25, 0.5, 0.75, 1.0];
Y = [0, 0.32, 0.82, 1.59, 2.72];
plot(X,Y)
b)
c)
d) Trapecio:
function salida=trapecios(f,a,b,n);
h=(b-a)/n; %calcula la distancia entre los intervalos
integral=f(a)+f(b);
nodo=a+h;
for k=1:(n-1)
integral=integral+2*f(nodo);
nodo=nodo+h;
end
integral=(integral*h)/2;
salida=integral;
Simpson:
function salida=simpson(f,a,b,n);
h=(b-a)/(2*n);
simpson=f(a)+f(b);
nodo=a+h;
for k=1:(n-1)
simpson=simpson+4*f(nodo);
nodo=nodo+h;
simpson=simpson+2*f(nodo);
nodo=nodo+h;
end
simpson=simpson+4*f(nodo);
simpson=(simpson*h)/3;
salida=simpson;
e)
Método
Trapecio
Simpson
Valor de la integral
1.0026
1.0026
f)
a) El valor de la integral es el mismo. En la regla de Simpson basta con coger un n=1,
mientras que la regla del trapecio necesita más valores (n=12) para obtener el mismo
valor de la integral. El valor es el esperado ya que el error en ambas va a ser menor
que 0.005, y por tanto obtendremos el mismo valor.
b)
Si en la regla del trapecio cogemos un n menor (n=7) obtendremos un valor de la
integral mayor al del apartado e:
En cambio, si cogemos un n mayor (n=14) el valor de la integral será menor:
Por otra parte, si cogemos un n mayor (n=4) en la regla de Simpson obtendremos un
valor menor: