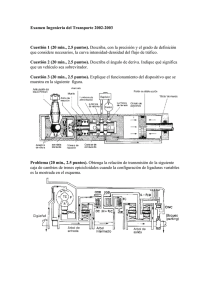
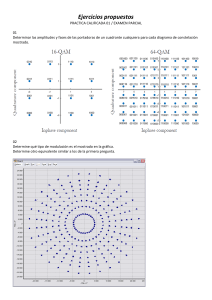
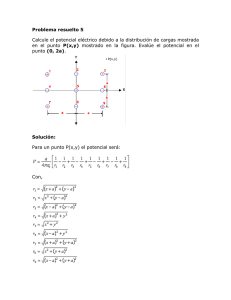
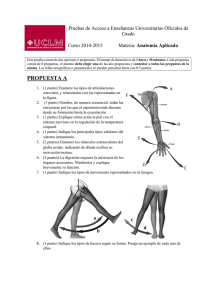
UNIVERSIDAD NACIONAL DE INGENIERÍA Facultad de Ingeniería Civil Departamento Académico de Estructuras EXAMEN PARCIAL DE ANALISIS ESTRUCTURAL I Profesora Día y hora Ciclo 2019-2 (EC211-J) : GIBU YAGUE, Patricia : Miércoles 09 de Octubre 2019 Indicaciones : Sin copias ni apuntes ni elementos de consulta. Prohibido el préstamo de calculadoras y correctores, uso de celulares. Importante: Sustente sus procedimientos y respuestas Tiempo total: 110min TEORIA Y CONCEPTOS: Responder al principio de la prueba en la primera cara de su cuadernillo – máx. 20min) PREGUNTA 1 (3 puntos) Responder brevemente de acuerdo a las lecturas o lo discutido en clase solo 3 de las siguientes preguntas a) ¿Qué ventajas tiene usar el método de trabajo virtual, respecto al del teorema de Castigliano? b) ¿Por qué el asentamiento o desplazamiento especificado de un apoyo desarrolla trabajo virtual externo y no energía interna? Explique c) ¿Cuándo una estructura es estable? ¿qué condiciones debe cumplir? Que características de la estructura lograrán dichas condiciones de estabilidad d) “El sistema virtual Q desarrolla trabajo virtual externo WQ”. Explique por que esta expresión es falsa e) Defina el coeficiente de flexibilidad, indique que significan sus índices i, j PREGUNTA 2 (2 puntos) -Leer con atención: No se resuelve numéricamente Considere la estructura hiperestática mostrada. Para resolver por el método de las fuerzas se pueden plantear diferentes estructuras fundamentales (o isostatizadas) a) ¿Cuántas incógnitas (redundantes) hay? b) ¿Cuántos casos se superponen? c) Plantee al menos 2 alternativas de dichas estructuras fundamentales equivalentes e indique que condiciones debe cumplir d) (+1p) Elija una de las alternativa de c) y dibuje los esquemas de las deformadas que corresponden a los casos de superposición (cada una con su deformada y que muestre las deflexiones io y ij) y plantee las ecuaciones de compatibilidad Importante: la nomenclatura de sus esquemas sea acorde a los términos en sus ecuaciones FORMULAS UTILES: 𝒅𝒊 = ∑ 𝒔𝑺𝑳 𝑬𝑨 𝒅𝒙 𝒅𝒙 𝒅𝒙 𝒅𝒙 + ∑ ∫ 𝑴𝒎 + ∑ ∫ 𝒌𝒗𝑽 + ∑ ∫ 𝑴𝒕 𝒎 𝑬𝑨 𝑬𝑰 𝑮𝑨 𝑮𝑱 𝑭𝑷 𝑳 ∑ 𝑸𝜹𝑷 = ∑ 𝑭𝑸 ∗ ( + 𝜶∆𝑻𝑳 + ∆𝑳𝒇𝒂𝒃𝒓 ) 𝑬𝑨 𝒅𝒊 = ∑ ∫ 𝒏𝑵 PROBLEMAS. Resuelva en forma ordenada, consecutiva D PREGUNTA 3 (5 puntos) (Teorema de Castigliano, forma (5000) PREGUNTA 4 (5 puntos) (Método carga unitaria) a) Calcule el desplazamiento horizontal en B en la estructura mostrada. Desarrolle la expresión literal. b) Para los valores numéricos q=2.5t/m, r=3m, evalúe la expresión que obtuvo en (a) A ) 000 (15 En la armadura mostrada se expresan las secciones en cada barra en mm2, E=12000 MPa a) (3) Determine el desplazamiento horizontal de C b) (2) ¿Cuál es la carga horizontal que se debe aplicar en C para que su desplazamiento horizontal sea cero? c) (+1, opcional) Explique con un esquema a que caso hiperestático correspondería la pregunta (b) e indique como usaría su respuesta en (a) (15 00 0) general) (15000) C (15000) B 24kN B q EI constante (sólo flexión) C A PREGUNTA 5 (5 puntos) (Método trabajo virtual) En la armadura mostrada la sección de las barras AB, BD y CD es de 4plg2, el área de las demás es de 2.5plg2. E= 29000ksi. a) Calcule el desplazamiento vertical de C generado por las cargas mostradas si además la barra BD se fabrica 0.5plg más cortas y el apoyo D tiene un asentamiento de 0.3plg