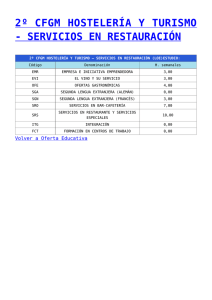
Educación Matemática Realista Hans Freudenthal (1905 - 1990) Principios de la EMR 1. La exploración fenomenológica. La búsqueda de fenómenos ricos, significativos y no pre-estructurados con vías a desarrollar en los alumnos nociones intuitivas que los lleven a la formación de objetos matemáticos. Principios de la EMR 1. La exploración fenomenológica. 2. El uso de modelos y símbolos. Proceso de matematización progresiva apoyado por una gran variedad de modelos Principios de la EMR 1. La exploración fenomenológica. 2. El uso de modelos y símbolos. 3. El uso de construcciones y producciones de los alumnos. Es esencial que los alumnos hagan uso de sus construcciones y producciones durante los procesos de aprendizaje, ya que esto les da significación. Principios de la EMR 1. La exploración fenomenológica. 2. El uso de modelos y símbolos. 3. El uso de construcciones y producciones de los alumnos. 4. La interacción. Las contribuciones de diversos alumnos pueden ser comparadas y contrastadas lo cual permite reflexionar acerca de la actividad matematizadora, tanto la propia como la de otros. Principios de la EMR 1. La exploración fenomenológica. 2. El uso de modelos y símbolos. 3. El uso de construcciones y producciones de los alumnos. 4. La interacción. 5. El entrecruzado de ejes y temas curriculares Es importante considerar a las secuencias didácticas en sus múltiples interrelaciones. Matematización Progresiva Freudenthal propone enseñarles a los alumnos a matematizar, distingue dos dimensiones en la matematización: horizontal y vertical. Horizontal: Consiste en convertir un problema de la realidad en un problema matemático haciendo uso del sentido común, la intuición, la observación, la aproximación empírica y la experimentación inductiva. Vertical: consiste en moverse dentro de la realidad matemática haciendo uso de la esquematización, la generalización, la prueba, el rigor y la simbolización. Niveles de Matematización Una maestra necesita cortar trozos de piolín de 2,75 m. Ella tiene un ovillo de piolín de 80 metros. ¿Cuántos trozos de piolín puede cortar? Contextos y Situaciones Una situación es realista en tanto se presenta ante el sujeto como realizable, razonable o imaginable (Freudenthal, 1973, 1991; van den HeuvelPanhuizen, 1996). Contextos y Situaciones Cuando un contexto es significativo para el alumno, éste sirve de punto de partida para su actividad matemática en tanto moviliza su sentido común y sugiere el uso de estrategias informales ligadas a la situación en cuestión. Es importante subrayar que el que un contexto sea o no realista depende de la experiencia previa del alumno y/o de su capacidad para imaginarlo o visualizarlo. Contextos y Situaciones Desde este punto de vista resulta tan “real” o “realista” para un alumno del primer ciclo trabajar en torno a situaciones que involucran cambios en el número de pasajeros de un autobús durante distintas trayectorias como lo será, años más tarde, trabajar directamente con el lenguaje de flechas como herramienta para simbolizar tales cambios (van der Brink, 1991), abriendo la puerta al trabajo con operadores y ecuaciones en los años superiores. Contextos y Situaciones MODELOS MODELOS MODELOS MODELOS Interacción y Reflexión Interacción y Reflexión Interacción y Reflexión Interacción y Reflexión Etapas para la EMR Etapas para la EMR Etapas para la EMR