FIUBA 2022
Análisis Matemático II
20221022P1
p
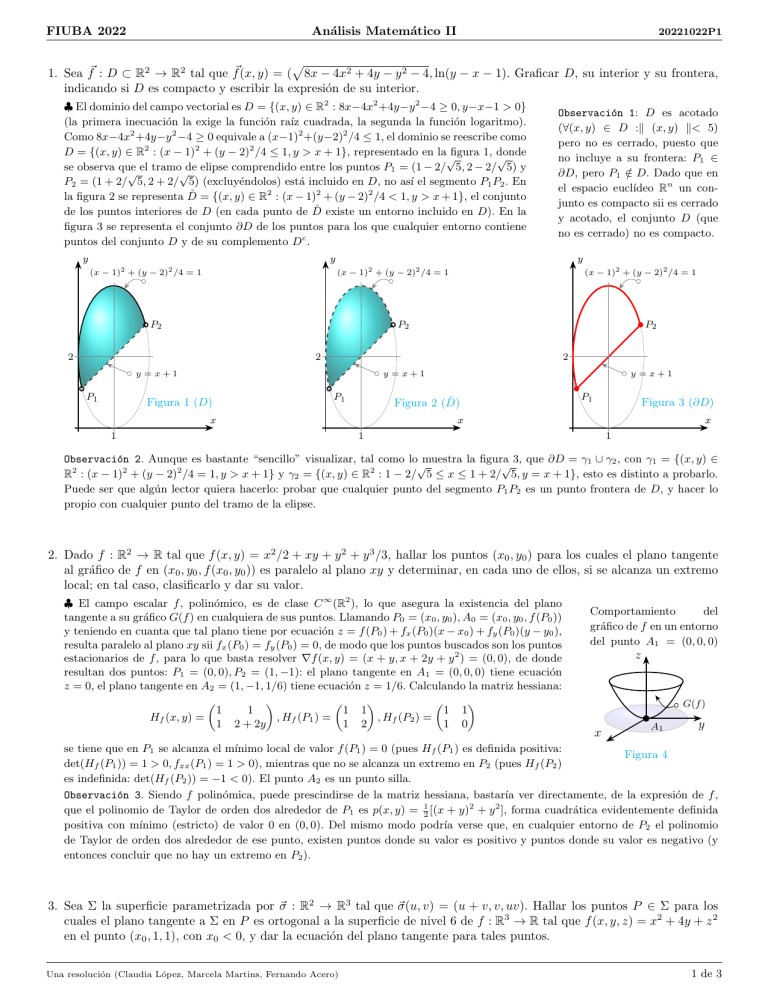
1. Sea f~ : D ⊂ R2 → R2 tal que f~(x, y) = ( 8x − 4x2 + 4y − y 2 − 4, ln(y − x − 1). Graficar D, su interior y su frontera,
indicando si D es compacto y escribir la expresión de su interior.
♣ El dominio del campo vectorial es D = {(x, y) ∈ R2 : 8x−4x2 +4y−y 2 −4 ≥ 0, y−x−1 > 0}
(la primera inecuación la exige la función raı́z cuadrada, la segunda la función logaritmo).
Como 8x−4x2 +4y−y 2 −4 ≥ 0 equivale a (x−1)2 +(y−2)2 /4 ≤ 1, el dominio se reescribe como
D = {(x, y) ∈ R2 : (x − 1)2 + (y − 2)2 /4 ≤ 1, y > x + 1}, representado en la figura 1, donde
√
√
se observa que el tramo de elipse comprendido entre los puntos P1 = (1 − 2/ 5, 2 − 2/ 5) y
√
√
P2 = (1 + 2/ 5, 2 + 2/ 5) (excluyéndolos) está incluido en D, no ası́ el segmento P1 P2 . En
la figura 2 se representa D̊ = {(x, y) ∈ R2 : (x − 1)2 + (y − 2)2 /4 < 1, y > x + 1}, el conjunto
de los puntos interiores de D (en cada punto de D̊ existe un entorno incluido en D). En la
figura 3 se representa el conjunto ∂D de los puntos para los que cualquier entorno contiene
puntos del conjunto D y de su complemento Dc .
y
Observación 1: D es acotado
(∀(x, y) ∈ D :k (x, y) k< 5)
pero no es cerrado, puesto que
no incluye a su frontera: P1 ∈
∂D, pero P1 ∈
/ D. Dado que en
el espacio euclı́deo Rn un conjunto es compacto sii es cerrado
y acotado, el conjunto D (que
no es cerrado) no es compacto.
y
(x − 1)2 + (y − 2)2 /4 = 1
y
(x − 1)2 + (y − 2)2 /4 = 1
P2
(x − 1)2 + (y − 2)2 /4 = 1
P2
2
P2
2
2
y =x+1
P1
y =x+1
Figura 1 (D)
P1
Figura 2 (D̊)
x
1
y =x+1
P1
Figura 3 (∂D)
x
x
1
1
Observación 2. Aunque es bastante “sencillo” visualizar, tal como lo muestra la figura 3, que ∂D = γ1 ∪ γ2 , con γ1 = {(x, y) ∈
√
√
R2 : (x − 1)2 + (y − 2)2 /4 = 1, y > x + 1} y γ2 = {(x, y) ∈ R2 : 1 − 2/ 5 ≤ x ≤ 1 + 2/ 5, y = x + 1}, esto es distinto a probarlo.
Puede ser que algún lector quiera hacerlo: probar que cualquier punto del segmento P1 P2 es un punto frontera de D, y hacer lo
propio con cualquier punto del tramo de la elipse.
2. Dado f : R2 → R tal que f (x, y) = x2 /2 + xy + y 2 + y 3 /3, hallar los puntos (x0 , y0 ) para los cuales el plano tangente
al gráfico de f en (x0 , y0 , f (x0 , y0 )) es paralelo al plano xy y determinar, en cada uno de ellos, si se alcanza un extremo
local; en tal caso, clasificarlo y dar su valor.
♣ El campo escalar f , polinómico, es de clase C ∞ (R2 ), lo que asegura la existencia del plano
tangente a su gráfico G(f ) en cualquiera de sus puntos. Llamando P0 = (x0 , y0 ), A0 = (x0 , y0 , f (P0 ))
y teniendo en cuanta que tal plano tiene por ecuación z = f (P0 ) + fx (P0 )(x − x0 ) + fy (P0 )(y − y0 ),
resulta paralelo al plano xy sii fx (P0 ) = fy (P0 ) = 0, de modo que los puntos buscados son los puntos
estacionarios de f , para lo que basta resolver ∇f (x, y) = (x + y, x + 2y + y 2 ) = (0, 0), de donde
resultan dos puntos: P1 = (0, 0), P2 = (1, −1): el plano tangente en A1 = (0, 0, 0) tiene ecuación
z = 0, el plano tangente en A2 = (1, −1, 1/6) tiene ecuación z = 1/6. Calculando la matriz hessiana:
1
1
1 1
1 1
Hf (x, y) =
, Hf (P1 ) =
, Hf (P2 ) =
1 2 + 2y
1 2
1 0
Comportamiento
del
gráfico de f en un entorno
del punto A1 = (0, 0, 0)
z
G(f )
x
A1
y
se tiene que en P1 se alcanza el mı́nimo local de valor f (P1 ) = 0 (pues Hf (P1 ) es definida positiva:
Figura 4
det(Hf (P1 )) = 1 > 0, fxx (P1 ) = 1 > 0), mientras que no se alcanza un extremo en P2 (pues Hf (P2 )
es indefinida: det(Hf (P2 )) = −1 < 0). El punto A2 es un punto silla.
Observación 3. Siendo f polinómica, puede prescindirse de la matriz hessiana, bastarı́a ver directamente, de la expresión de f ,
que el polinomio de Taylor de orden dos alrededor de P1 es p(x, y) = 12 [(x + y)2 + y 2 ], forma cuadrática evidentemente definida
positiva con mı́nimo (estricto) de valor 0 en (0, 0). Del mismo modo podrı́a verse que, en cualquier entorno de P2 el polinomio
de Taylor de orden dos alrededor de ese punto, existen puntos donde su valor es positivo y puntos donde su valor es negativo (y
entonces concluir que no hay un extremo en P2 ).
3. Sea Σ la superficie parametrizada por ~σ : R2 → R3 tal que ~σ (u, v) = (u + v, v, uv). Hallar los puntos P ∈ Σ para los
cuales el plano tangente a Σ en P es ortogonal a la superficie de nivel 6 de f : R3 → R tal que f (x, y, z) = x2 + 4y + z 2
en el punto (x0 , 1, 1), con x0 < 0, y dar la ecuación del plano tangente para tales puntos.
Una resolución (Claudia López, Marcela Martins, Fernando Acero)
1 de 3
FIUBA 2022
Análisis Matemático II
20221022P1
♣ Llamando A0 = (x0 , 1, 1) y dado que A0 ∈ C6 (f ), por definición debe ser
∇Φ(P )
f (A0 ) = x20 + 4(1) + 12 = 6, de donde x20 = 1 y entonces (ya que x0 < 0) es
π
x0 = −1, luego ya se sabe que A0 = (−1, 1, 1). Como, por otra parte f es diferΣ = C0 (Φ)
3
∞
3
enciable en R (de hecho, es C (R )), se tiene que un vector normal a C6 (f )
en A0 es ∇f (A0 ); siendo ∇f (x, y, z) = (2x, 4, 2z), es ∇f (A0 ) = (−2, 4, 2).
Como el plano tangente π a Σ en P debe ser ortogonal a la recta de ecuación
P
X = A0 + µ∇f (A0 ), µ ∈ R, la superficie Σ misma ha de ser, en P , normal
C6 (f )
a ∇f (A0 ). Dado que (x, y, z) = (u + v, v, uv), es z = (x − y)y, de modo que
Σ = C0 (Φ), definiendo Φ(x, y, z) = (x − y)y − z, y entonces, el problema se
∇f (A0 )
reduce a hallar los puntos P = (x, y, z) ∈ Σ tales que ∇Φ(P ) = λ∇f (A0 ),
para algún λ real:(−y, −x + 2y, 1) = λ(−2, 4, 2), z = (x − y)y, sistema que
tiene por solución λ = 1/2, x = 0, y = 1, z = −1, de modo que el (único) punto
A0
Figura 5
es P = (0, 1, −1). La ecuación del plano π es entonces (X − P ) · (−1, 2, 1) = 0,
que escrita en forma normal es −x + 2y + z = 1.
Observación 4. En lugar de subsumir Σ en un conjunto de nivel del campo escalar Φ, también pudo plantearse, en su lugar,
que el producto vectorial fundamental de la parametrización regular ~σ fuese un múltiplo del vector ∇f (A0 ), esto es determinar
u, v tales que ~σu (u, v) × ~σv (u, v) = α∇f (A0 ), para algún real α, y ulteriormente determinar el punto P como la imagen a través
de ~σ del par (u, v) ası́ obtenido. Resolviendo la igualdad ~σu (u, v) × ~σv (u, v) = α∇f (A0 ) es (−v, v − u, 1) = α(−2, 4, 2) resulta
α = 1/2, u = −1, v = 1, de modo que P = ~σ (−1, 1) = (0, 1, −1), como se obtuviera anteriormente.
4. Justificar, mediante el teorema de la función implı́cita, que existe z0 ∈ R tal que la ecuación ex z + yz 2 + z 3 = 1 define
en un entorno del punto (x0 , y0 ) = (0, −1) la función z = h(x, y) de clase C 1 en ese entorno y que cumple h(0, −1) = z0 .
Calcular una aproximación lineal de h(0.1, −1.05) y hallar el versor que hace máxima la derivada direccional de h en el
punto (0, −1).
♣ Definiendo f : R3 → R tal que f (x, y, z) = ex z + yz 2 + z 3 − 1, que es
C ∞ (R3 ), y llamando P0 = (0, −1) y A0 = (0, −1, z0 ), se tiene que la ecuación
f (x, y, z) = 0 es satisfecha por A0 sii f (A0 ) = z0 − z02 + z02 − 1 = (z0 −
1)(z02 + 1) = 0 sii z0 = 1 ( luego A0 = (0, −1, 1) cumple f (A0 ) = 0), y siendo
fz (x, y, z) = ex + 2yz + 3z 2 , fz (A0 ) = 1 − 2 + 3 = 2 6= 0, el teorema de la
función implı́cita, asegura, en un entorno E(P0 ), la existencia de un único
campo escalar h : E(P0 ) ⊂ R2 → R de clase C 1 (E(P0 )) tal que h(P0 ) = 1
y tal que ∀(x, y) ∈ R2 ∈ E(P0 ) : f (x, y, h(x, y)) = 0, y además ∇h(P0 ) =
(−1/fz (A0 ))(fx (A0 ), fy (A0 ). Como fx (x, y, z) = ex z, fx (A0 ) = 1, fy (x, y, z) =
z2 , fy (A0 ) = 1, se tiene que ∇h(P0 ) = (−1/2, −1/2).
π
A0
G(h)
Figura 6
El gráfico del polinomio de Taylor de orden 1 de h en P0 es el plano π, tangente al gráfico G(h) en A0 y su ecuación es p(x, y) =
h(P0 ) + hx (P0 )x + hy (P0 )(y + 1) = 1 − (1/2)x − (1/2)(y + 1), de modo que p(0.1, −1.05) = 1 − (1/2)(0.1) − (1/2)(−0.05) = 0.975
es una aproximación lineal de h(0.1, −1.05). Finalmente, siendo h diferenciable, la derivada direccional en P0 √
en la dirección
de
√
un versor v̌ es fv̌ (P0 ) = ∇h(P0 ) · v̌, producto escalar que se hace máximo con v̌ =√
∇h(P0 )/ k ∇h(P0 ) k= (−1/ 2, −1/ 2) (en la
dirección de tal versor la derivada direccional toma el valor máximo k ∇h(P0 ) k= 2/2).
Observación 5. Siendo h diferenciable en P0 , cualquiera sea el versor v̌ se tiene que hv̌ (P0 ) = ∇h(P0 ) · v̌, y entonces
− k ∇h(P0 ) k≤ hv̌ (P0 ) ≤k ∇h(P0 ) k
alcanzándose min{hv̌ (P0 )} = − k ∇h(P0 ) k con (únicamente) v̌ = −∇h(P0 )/ k ∇h(P0 ) k, y el max{hv̌ (P0 )} =k ∇h(P0 ) k con
(únicamente) v̌ = ∇h(P0 )/ k ∇h(P0 ) k.
5. Probar que el campo escalar f : R2 → R admite en P0 = (0, 0) derivadas direccionales en todas las direcciones, calcular
sus derivadas parciales en ese punto y determinar todos los versores v̌ para los que fv̌ (P0 ) = 0.
(
f (x, y) =
Una resolución (Claudia López, Marcela Martins, Fernando Acero)
sin(x3 )−y 3
x2 +2y 2
0
si (x, y) 6= (0, 0)
si (x, y) = (0, 0)
2 de 3
FIUBA 2022
Análisis Matemático II
20221022P1
y
?
2
2
♣ Sean E (P0 ) un entorno reducido de P0 , un cualquier versor v̌ = (a, b) con a + b = 1
y h 6= 0 tal que P o + hv̌ ∈ E ? (P0 ); en tal caso el valor f (P o + hv̌) se calcula mediante la
primera rama de la función f , siendo entonces f (P0 + hv̌) = (sin(h3 a3 ) − h3 b3 )/(h2 + h2 b2 ),
mientras que f (P0 ) = 0, tal como lo define la segunda rama de f . De esta manera, el cociente
incremental es (f (P0 + hv̌) − f (P0 ))/h = (sin(h3 a3 ) − h3 b3 )/(h3 + h3 b2 ), de modo que, por
definición, es
def
fv̌ (P0 ) = lim
h→0
f (P0 + hv̌) − f (P0 )
sin(h3 a3 ) − h3 b3
1
a3 − b3
=
lim
=
2
3
h
1 + b h→0
h
1 + b2
E ? (P0 )
P0 + hv̌
x
P0
con a2 +b2 = 1
Figura 7
3 3
3 3
3 3
3 3
a )
a )
a )
a )
La última igualdad resulta de que, si a 6= 0, es sin(h
= a3 sin(h
de modo que (a 6= 0) es limh→0 sin(h
= a3 limh→0 sin(h
=
h3
a3 h3
h3
a3 h3
3
3
3
a ; si en cambio, a = 0 el lı́mite es directamente 0, que también es a = 0 = 0, de modo que, cualquiera sea a (con |a| ≤ 1) es
3 3
a )
limh→0 sin(h
= a3 .
h3
Para asegurar la existencia de las derivadas direccionales, no alcanza con la obtención de la expresión anterior: se requiere examinar
el denominador. Dado que el denominador de la expresión anterior no se anula, pues 1 ≤ 1 + b2 ≤ 2, las derivadas direccionales
existen para todos los versores v̌.
En particular, las derivadas parciales se obtienen para los versores canónicos (1, 0) y (0, 1), de modo que fx (P0 ) = 1, fy (P0 ) = −1/2.
2
2
Finalmente, las derivadas direccionales son nulas√
sii el numerador
de la expresión es
√
√ nulo, esto
√ es sii a = b, y puesto que a + b = 1,
esto se produce (solamente) o bien con v̌1 = (1/ 2, 1/ 2), o bien con v̌2 = (−1/ 2, −1/ 2).
Observación 6. Aunque no se pregunta aquı́, el campo escalar no es diferenciable en P0 , lo que puede probarse de muchos modos.
Uno de ellos, que aprovecha el cálculo ya hecho, argumenta que si fuera diferenciable, las derivadas direccionales nulas se obtienen en
direcciones normales al ∇f (P0 ) = (1, −1/2), que no es el caso de los versores obtenidos. Otro argumento descarta la diferenciabilidad
desde el vamos, pues f tiene una discontinuidad esencial en P0 , lo que puede verse examinando el lı́mite por dos caminos que
ciertamente pasan por P0 , tales como γ1 = {(x, y) ∈ R2 : sin(x3 ) − y 3 = 0}, γ2 = {(x, y) ∈ R2 : sin(x3 ) − x2 − 2y 2 − y 3 = 0}. Por
el primer camino, el lı́mite resulta nulo, por el segundo vale 1, de modo que (por la unicidad del lı́mite) no existe limP →P0 f (P ),
la discontinuidad es entonces esencial en P0 y el campo ya no puede ser diferenciable en ese punto (se supone sabido que la
continuidad es una condición necesaria de la diferenciabilidad).
Una resolución (Claudia López, Marcela Martins, Fernando Acero)
3 de 3









