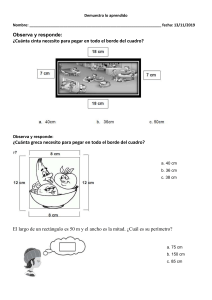
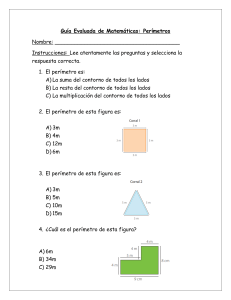
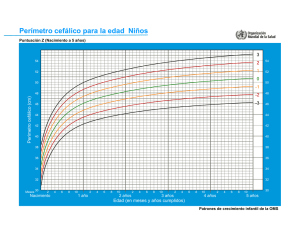
SESIÓN DE APRENDIZAJE Resolvemos problemas con cuadriláteros DATOS INFORMATIVOS: Institución educativa: 0014 “Andrés Bello” Fecha: 04 de octubre 2022. Docente: Percy Brayam Balbuena Cardich. Grado : 3º Sección: “C” PROPÓSITOS DE APRENDIZAJE: Matemática Área Competencia Resuelve problemas forma, movimiento localización Desempeños de y Resuelve problemas en los que modela las características y la ubicación de objetos del entorno a formas bidimensionales y tridimensionales, sus propiedades, su ampliación, reducción o rotación. Describe y clasifica prismas rectos, cuadriláteros, triángulos, círculos, por sus elementos: vértices, lados, caras, ángulos, y por sus propiedades; usando lenguaje geométrico.. Emplea procedimientos e instrumentos para estimar o medir la longitud, superficie y capacidad de los objetos, seleccionando la unidad de medida convencional apropiada y realizando conversiones Evidencia Resuelve problemas con cuadriláteros e identifica diversas estrategias para establecer sus medidas. Enfoques transversales Actitudes o acciones observables Se desenvuelve en los entornos virtuales Los estudiantes hacen uso de aplicaciones digitales para desarrollar actitudes del razonamiento lógico matemática. De Orientación al bien común. Los estudiantes respetan brindando oportunidades de convivencia y aprendizaje. SECUENCIA DIDÁCTICA DE LA SESIÓN Inicio: tiempo estimado 10 minutos. A nivel de aula: Saluda a los estudiantes cordialmente dándoles la bienvenida y expresarles la alegría de empezar a trabajar el área de matemática. Recoge los saberes previos de los niños y las niñas a través de las siguientes preguntas: ¿Alguna vez has identificado la medida de los lados de un cuadrilátero?, ¿Cómo lo hiciste?, ¿Con que propósito lo hiciste?, ¿En qué lugar lo aplicaste? Comunica el propósito de la sesión: Usaremos estrategias aditivas o multiplicativas para resolver problemas con cuadriláteros, usando la aplicación Jclic en el AIP. Observando los acuerdos de convivencia del aula de Innovación Pedagógica, propone con los estudiantes 3 acuerdos que les permitirán trabajar en un clima favorable para la presente sesión. Desarrollo: tiempo estimado 100 minutos. Comprensión y familiarización del problema. En pares: Invita a cada par de estudiantes a leer con mucha tención el problema propuesto “Patty, para sus maquetas representadas en las figuras 1 y 2, planea colocar árboles en los puntos rojos que están separados una distancia de 5 cm uno de otro. ¿Cuánto miden los lados de cada maqueta? ¿Cuántos árboles colocará en cada una?” Comenten con su compañera o compañero cómo podrían resolver el problema e induce a la comprensión del problema respondiendo las siguientes preguntas: ¿De qué trata el problema?, ¿Qué datos nos brinda?, ¿Qué nos pide hallar el problema? Búsqueda y aplicación de la estrategia. A nivel grupal: Para buscar la estrategia más adecuada para resolver el problema proponles las siguientes preguntas: ¿Qué deberíamos hacer primero?, ¿Cómo haríamos para resolver el reto que se nos ha propuesto?, ¿Qué operación matemática utilizaremos?, ¿Qué material utilizaremos para representar el problema?, motiva a que ellos generen sus propias cuestiones para hallar la estrategia más acertada y escriben el procedimiento a seguir en un papelote. Realizan la aplicación de la estrategia elegida ¿Consideras que los procedimientos a seguir te ayudaran a cumplir el reto planteado?, ¿Cuál es procedimiento a seguir?, ¿Qué debemos hacer primero? Entrégales papelotes y plumones de colores e indícales que, deben realizar la actividad Socialización del problema. A nivel de aula: Eligen a un representante de su par para que exponga sus conclusiones al grupo clase. Durante la presentación de los resultados realiza las siguientes preguntas: ¿Qué es lo que se representó?, ¿El material les ayudó en la representación de lo que pidió el problema?, ¿Cómo realizaron la representación utilizando el material?, ¿Cómo determinaron la solución al problema? Reflexión y formalización. A nivel de aula: En grupo clase, dialogan sobre los procesos desarrollados. Pregúntales: ¿Crees qué las estrategias que has utilizado te han ayudado para logara el reto?, ¿Les pareció que este reto es parecido a lo que hiciste alguna vez?, ¿Creen que es importante identificar las características de los cuadriláteros? Formaliza el conocimiento: Perímetro de un rectángulo Sea un rectángulo cuyos lados son iguales dos a dos de longitud a=3 cm y b=5 cm. Su perímetro será dos veces la suma de dos lados contiguos: Y se obtiene que el perímetro del rectángulo de lados a=3 cm y b=5 cm es de 16 cm. Perímetro de un cuadrado Multiplica la longitud del lado por 4 para hallar el perímetro. Toma la longitud del lado L que acabas de calcular y conéctalo en la fórmula del perímetro, P = 4L. ¡El resultado será el perímetro del cuadrado P= 5x4 = 20 ó 5+5+5+5= 20 Planteamiento de otros problemas. A nivel de aula: En el AIP desarrollamos ejercicios y resolvemos problemas en la aplicación JCLIC M20. Luego indícales que cada equipo debe superar el reto de crear un problema similar con una casuística relacionada a su contexto escolar o social y lo socializan con sus compañeros de aula. En el aula de clases. Cierre: tiempo estimado 10 minutos. A nivel individual. Se plantea las siguientes preguntas de metacognición: ¿Qué aprendí?, ¿Tuve alguna dificultad para aprenderlo y como lo superaste? ¿En qué me servirá lo aprendido hoy? El patio del colegio es un cuadrilátero según se observa, ¿cuántos metros de banderines se necesita para colocar alrededor del patio? 25 m 20 m 20 m 48 m c) El perímetro de un salón cuadrado es 80 m. Si deseo colocar zócalos a lo largo de cada pared, ¿cuánto medirá el zócalo de una pared? d) En un parque han dejado espacios en forma de rombo para 6 plantas. Si se compró 48 m de cerco para las 6 plantas y se sabe que los rombos de cada planta son iguales, ¿cuánto mide el lado de cada rombo? GUÍA DE OBSERVACIÓN Grado Sección y 3º “C” Clasificamos cuadriláteros Competencia Resuelve problemas de forma, movimiento y localización Expresa con dibujos su comprensión sobre los elementos y propiedades del N° NOMBRES Y APELLIDOS rectángulo con relación a la medida de su perímetro. 1 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. Matemática AREA 2 3 LEYENDA: 1.Incio 2.Proceso 3.Logrado Emplea la unidad de medida no convencional o convencional, según convenga, así como instrumentos de medición, y diversos recursos. 1 2 3 Propone al menos una estrategia para resolver el problema y explica cómo se organizará para lograr las metas. 1 2 3 LOGRO