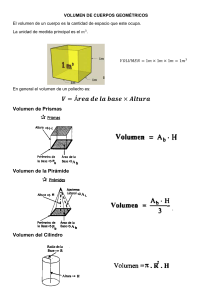
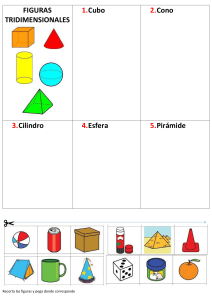
INSTITUCIÓN EDUCATIVA JEC N° 6037 “ Inca Pachacutec” S.J.M.- UGEL 01 SEMANA 32 Del 22 al 26/Nov. EXPERIENCIA DE APRENDIZAJE 9: Nuestro Bicentenario nos desafía a promover acciones responsables para valorar y conservar nuestro patrimonio natural Área MATEMATICA Docente Competencia ALICIA LOVON Teléfono 989387305 Grado Correo 3ero* B,C [email protected] RESUELVE PROBLEMAS DE FORMA MOVIMENTO Y LOCALIZACIÓN Propósito Determinar las variaciones en la temperatura ambiental de una comunidad andina haciendo uso de los números enteros(Z) Indicaciones Lee detenidamente las definiciones y resuelve los actividades ACTIVIDAD 6: Elaboramos una cono-maceta para la conservación de plantas oriundas de nuestro Perú CUERPOS DE REVOLUCION Los cuerpos de revolución son los cuerpos geométricos que se forman al girar una figura plana alrededor de un eje. PRINCIPALES CUERPOS DE REVOLUCIÓN del cilindro. Volumen del cilindro = π · r2 · h El volumen del cono es la tercera parte del volumen del cilindro. Por lo tanto, la expresión es la siguiente: h: altura r: radio g: generatriz del cono (hipotenusa del triángulo rectángulo) Volumen del cilindro = π · r2 · h La unidad de medida del volumen puede ser: cm3, m3 o km3. AREA DEL CONO: El área del cono es toda la superficie externa,es decir el área de base,más el área EL CONO: El cono circular recto o de revolución es el sólido generado por una región triangular (limitada por un triángulo rectángulo) cuando gira una vuelta alrededor de uno de sus catetos. Para calcular el volumen de un cono debemos conocer la expresión que calcula el volumen Pá gina 1|4 INSTITUCIÓN EDUCATIVA JEC N° 6037 “ Inca Pachacutec” S.J.M.- UGEL 01 lateral SITUACIÓN 1: Pedro preparó unos chocolates en forma de cono con las medidas que se indican. Ahora, quiere envolverlos con papel platino. ¿Cuál será la superficie que cubrirá la envoltura? Solución: Para calcular el área de la base, debemos saber cuánto mide el radio. Como la generatriz, la altura y el radio forman un triángulo rectángulo, aplicamos el teorema de Pitágoras. 3.- Ahora, tomamos el objeto, lo observamos atentamente y nos preguntamos: ¿Cómo se construyó? ¿Cómo fue antes de tomar esta forma? ¿Qué nombre reciben sus partes? Escribimos las respuestas ………………………………………………………………… ………………………………………………………………… ………………………………………………………………… ………………………………………………………………… ………………………………………………………………….. …………………………………………………………………………………………………… 4.- Registramos la información que nos proporciona el “gorro”, por ejemplo: la medida de su altura, diámetro, radio y generatriz. Tomamos nota en nuestro cuaderno. ….................................................................................................................................... ....................................................................................................................................... 5.- Vamos a desarmar el gorro para explorarlo y reconocer sus características. a. Identificamos la unión del material del cono y separamos los lados con mucho Exploramos un objeto de forma cónica 1.- Para iniciar la actividad necesitamos un gorro de fiesta infantil como el de la imagen. cuidado. Observamos atentamente qué ocurre y respondemos: 1.-¿Qué pasó con el cuerpo del cono? -------------------------------------------------------------------------------------------------------------2.-¿Qué forma tiene dicha pieza? ------------------------------------------------------------------------------------------------------------3.- ¿Qué nombre reciben los lados que estaban unidos? -------------------------------------------------------------------------------------------------------------- 2. -Observamos nuestro alrededor e identificamos objetos de forma semejante a la del gorro SITUACION: Nos preparamos para elaborar una cono Leonardo es un joven estudiante, responsable y amante de la naturaleza. Colecciona plantas en diferentes envases y macetas. Se ha propuesto diseñar una maceta diferente y novedosa que tenga una forma cónica, le sirva de almácigo y a la vez sea decorativa; en ella colocará semillas oriundas del Perú. Para ello, usará material reciclado de la zona (cartón, tela plástica u otro material del entorno). Lo Pá gina 2|4 INSTITUCIÓN EDUCATIVA JEC N° 6037 “ Inca Pachacutec” S.J.M.- UGEL 01 acompañaremos en su trabajo tomando en cuenta la siguiente imagen referencial: Calculamos el volumen de la cono-maceta Comprobemos que “el volumen del cono es la tercera parte del volumen de un cilindro de igual altura y diámetro”. Para ello, seguimos los siguientes pasos: 1. En la sección “Recursos para mi aprendizaje” encontraremos una plantilla llamada “Relación entre cilindro y cono”. Construimos el cilindro y el cono, y tomamos mediciones. a.-¿Qué conocimientos matemáticos tomará en cuenta Cesar al desarrollar la plantilla de la cono-maceta? ……………………………………………………………………………………………………………………………………………… ……………………………………………………………………………………………………………………………………………… …………………………………………………………………………………………………………………………………………….. b.-¿Qué materiales e instrumentos usará? ……………………………………………………………………………………………………………………………………………… ……………………………………………………………………………………………………………………………………………. C.-¿Qué procedimiento seguirá para lograrlo? ……………………………………………………………………………………………………………………………………………… ……………………………………………………………………………………………………………………………………………… ……………………………………………………………………………………………………………………………………………… d.-¿Qué cantidad de tierra necesitará para su cono-maceta? Para responder estas y otras interrogantes más, te invitamos a experimentar el proceso. ……………………………………………………………………………………………………………………………………………… ……………………………………………………………………………………………………………………………………………… Nos organizamos para diseñar la plantilla. Consideramos el tamaño de la cono-maceta, ya que servirá para hacer un pequeño almácigo. Preparamos los materiales e instrumentos, como cartulina, regla, transportador, compás, etc. para iniciar el trabajo. Elaboramos nuestra cono-maceta a.-¿Qué relación tienen las medidas de sus bases y alturas? ………………………………………………………………………………………………………………………………… ……………………………………………………………………………………………………………………………….. 2. Conseguimos arena o tierra. Luego, llenamos con arena o tierra el cono y vertimos el contenido en el cilindro. a.-¿Qué parte del cilindro se ha llenado? …………………………………….. ………………………………………. Repetimos la acción hasta que se llene el cilindro. b.- ¿Qué relación encontramos entre el volumen del cilindro y el volumen del cono? ¿A qué conclusión llegaremos? La describimos. ………………………………………………………………………………………………………………………………… ………………………………………………………………………………………………………………………………… Pá gina 3|4 INSTITUCIÓN EDUCATIVA JEC N° 6037 “ Inca Pachacutec” S.J.M.- UGEL 01 ……………………………………………………………………………………………………………………………………………… ……………………………………………………………………………………………………………………………………………… …………………………………………………………………………………………………………………………………………… 3. -Ahora ya puedes calcular el volumen de la cono-maceta. ¿Qué cantidad de tierra requiere? Pá gina 4|4 INSTITUCIÓN EDUCATIVA JEC N° 6037 “ Inca Pachacutec” S.J.M.- UGEL 01 Pá gina 5|4 INSTITUCIÓN EDUCATIVA JEC N° 6037 “ Inca Pachacutec” S.J.M.- UGEL 01 Pá gina 3|4 INSTITUCIÓN EDUCATIVA JEC N° 6037 “ Inca Pachacutec” S.J.M.- UGEL 01 Pá gina 4|4 INSTITUCIÓN EDUCATIVA JEC N° 6037 “ Inca Pachacutec” S.J.M.- UGEL 01 Pá gina 5|4