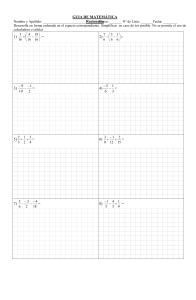
Expresiones Racionales
• Definición:
𝑎
𝑏
Así como llamamos números racionales a los números de la forma
con a y b enteros (𝑏 ≠ 0), llamaremos expresiones racionales a las
expresiones de la forma:
𝑃(𝑥)
𝑄 𝑥
Donde P(x) y Q(x) son polinomios de una sola variable x, siendo Q(x) no
nulo.
Simplificación de Expresiones Racionales
Es posible simplificarlas cuando existen factores comunes al numerador y al denominador,
de lo contrario, la expresión racional es irreducible.2
𝑥 −1
Consideremos la siguiente expresión: J(x) = 3
2
𝑥 +3𝑥 −𝑥−3
Primero factorizamos todo lo que sea posible del numerador y del denominador.
Numerador: es una diferencia de cuadrados x2 – 1 = (x + 1)(x – 1)
Denominador: mediante el Teorema de Gauss: los divisores del término independiente son
+1;-1;3;-3 ya que este polinomio es mónico (coeficiente principal igual a 1).
Ahora resta averiguar si alguno de estos valores es raíz con el Teorema del Resto:
𝟏3 + 3. 𝟏2 − 𝟏 − 3 = 0 por lo tanto x = 1 es raíz
Aplicamos división por Ruffini para
encontrar todas las raíces y así poder factorizar:
Cociente: x2 + 4x + 3
ecuación de segundo grado, aplicamos fórmula resolvente para
determinar si tiene más raíces reales y obtenemos x1 = -1; x2 = -3. Entonces las raíces
encontradas son x=1; x=-1; x=-3
Así llegamos a que el polinomio 𝑑𝑒𝑛𝑜𝑚𝑖𝑛𝑎𝑑𝑜𝑟 𝑥 3 + 3𝑥 2 − 𝑥 − 3, se puede escribir en
forma factorizada como: (x – 1)(x +1)(x + 3)
Las dos expresiones racionales anteriores son equivalentes. Es más sencillo trabajar con la
irreducible, pero sin perder de vista que el dominio de esta expresión pensada como función
es el que quedó determinado a partir de la expresión original.
Dom J(x) = ꭆ - {-1;1;-3}
Suma y Resta de Expresiones Racionales
Para sumar o restar dos o más expresiones racionales, debemos encontrar el
denominador común, siendo lo más conveniente tomar el mínimo común múltiplo
(mcm) de los denominadores.
mcm: Para hallarlo factorizamos los denominadores y luego multiplicamos los
factores comunes y no comunes con el mayor exponente con el que figuren.
La técnica para sumar o restar expresiones algebraicas racionales es la misma que
se emplea para la suma de fracciones numéricas:
𝑃 𝑄 𝑃𝑁 ∓ 𝑄𝑀
∓ =
𝑀 𝑁
𝑀. 𝑁
Multiplicación de Expresiones Racionales
El resultado de multiplicar dos expresiones algebraicas es otra
expresión algebraica fraccionaria cuyo numerador y denominador son
el producto de las expresiones dadas.
𝑷(𝒙) 𝑹(𝒙)
.
𝑸(𝒙) 𝑺 𝒙
=
𝑷 𝒙 . 𝑹(𝒙)
𝑸 𝒙 . 𝑺(𝒙)
𝟏
Debido a que su dominio es : 𝑹 − {−𝟐; 𝟎; 𝟐 : 𝟐}
División de Expresiones Racionales
El resultado de dividir dos expresiones algebraicas fraccionarias es otra
expresión que se obtiene multiplicando la primera expresión por la
recíproca de la segunda.
𝑷(𝒙)
𝑸 𝒙
:
𝑹(𝒙)
𝑺(𝒙)
=
𝑷(𝒙)
𝑸 𝒙
𝑺(𝒙)
.
𝑹 𝒙
Debido a que su dominio es : 𝑹 − {−𝟐; 𝟎}
Operaciones combinadas de Expresiones Racionales
Para resolver operaciones combinadas entre expresiones algebraicas fraccionarias se debe tener en
cuenta la simplificación, multiplicación, división, suma y resta de expresiones algebraicas
fraccionarias. Se pueden seguir los siguientes pasos:
1. Se separan los términos y se efectúan las operaciones indicadas en cada uno de ellos.
2. Se opera entre las expresiones semejantes
3. Se simplifica siempre que sea posible
4. Se indican las condiciones de posibilidad
Debido a que su dominio es : 𝑹 − {−𝟐; −𝟏}
5
Ɐ 𝐱 ∶ 𝐱 ≠ −𝟐 ᴧ 𝐱 ≠ 𝟐 ᴧ 𝐱 ≠ 3 ᴧ 𝐱 ≠
2
𝟓
𝑫𝒐𝒎: ℝ − −𝟐; 𝟐; 𝟐 ; 𝟑
Ecuaciones con Expresiones Racionales
• Ejercicio resuelto:
Verificación de resultados
Reemplazamos ese valor de x hallado en la ecuación original para
verificar que se cumple la igualdad:
3𝑥 2 − 11𝑥
6
𝑥−4
− 2𝑥 ∶
=
𝑥−3
4−𝑥
𝑥−3
3. 22 − 11. 2
6
2−4
− 2.2 ∶
=
2−3
4−2
2−3
12−22
(
−1
– 4) :
6
2
=
−2
−1
;
6:3=2 ;
2 = 2 se valida el resultado