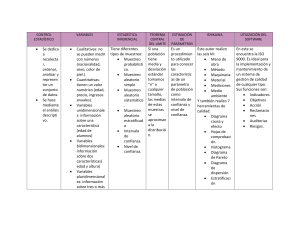
Estadística Inferencial Luis Ernesto Leyva Camargo Muestreo y distribuciones muestrales Estadística Estadística: Reto: Generalizar el conocimiento adquirido o experimentado Luis Ernesto Leyva Camargo Estadística inferencial Técnicas para obtener información sobre el comportamiento de una población. Implica, por lo regular, tomar decisiones sobre el grupo mayor del cual los datos forman parte. Trabajan con algún grado de incertidumbre. Se puede medir qué tan grande es la confianza de los resultados con base en el cálculo de las probabilidades. Luis Ernesto Leyva Camargo Población o universo Grupo de personas o elementos que tienen unas características comunes de las cuales se quiere obtener información. Luis Ernesto Leyva Camargo Censo valoración sobre la población completa. Luis Ernesto Leyva Camargo Muestra Muestra es una parte representativa de la población. Luis Ernesto Leyva Camargo Parámetro y estadístico Parámetro es una medida obtenida con los elementos de la población. Estadístico es una medida obtenida con los elementos de la muestra. Luis Ernesto Leyva Camargo Parámetro Estadístico Bases para la comparación Estadístico Parámetro Sentido La estadística es una medida que describe una fracción de la población. El parámetro se refiere a una medida que describe la población. Valor numérico Variable y Conocida Fijo y desconocido x̄ = Muestra de la media μ = media de la población Parámetros Vs Estadísticos σ = Desviación s = Desviación estándar estándar de la de la muestra población Notación estadística Luis Ernesto Leyva Camargo p̂ = Proporción de la muestra P = Proporción de la población x = Elementos de datos X = Elementos de datos n = Tamaño de la muestra N = Tamaño de la población r = coeficiente de correlación ρ = coeficiente de correlación Variables: Una variable es una característica que puede cambiar de valor en el tiempo y cuya variación es susceptible a adoptar diferentes valores, los cuales pueden medirse u observarse. Tipos de variables Cuantitativas Discretas (Enteros) Luis Ernesto Leyva Camargo Continuas (Reales) Cualitativas Dicotomizadas Nominales Ordinales (sin orden) (con orden) Escalas de medidas de variables Luis Ernesto Leyva Camargo Tipos de datos Tipos de datos Numéricos Discretos (conteos) Categóricos Continuos (medición) Luis Ernesto Leyva Camargo Dicotomizadas Nominales Ordinales (sin orden) (con orden) Tipos de Muestreo Tipos de muestreo Muestreo Aleatorio Simple MAS Con remplazo MCR Aleatorio No aleatorio (probabilístico) (no probabilístico) Muestreo por conglomerados Muestreo Estratificado Por conveniencia Subjetivo Sin Remplazo MAS Luis Ernesto Leyva Camargo Bola de nieve Por cuotas Muestreo aleatorio Se puede definir el conjunto de muestras posibles que se derivan del proceso de selección propuesto. A cada muestra le corresponde una probabilidad de selección p(s) conocida. El proceso de selección garantiza que todo elemento de la población tiene una probabilidad mayor a cero de ser incluido en alguna muestra. El proceso de selección propuesto consiste en un mecanismo aleatorio que garantiza que cada muestra s recibe exactamente la probabilidad p(s) de ser seleccionada. Luis Ernesto Leyva Camargo Para seleccionar n elemento de una población N Con remplazo: Muestreo Aleatorio Simple (MAS) Cada elemento seleccionado se puede volver a incluir. 1 Cada elemento mantiene una probabilidad constante 𝑁 Sin remplazo: Cada elemento seleccionado se no puede volver a incluir. 1 Cada elemento mantiene una probabilidad constante 𝑁−1 Luis Ernesto Leyva Camargo Para seleccionar n elemento de una población N Por conglomerado: Muestreo Aleatorio - Conglomerado - Estratificado En el muestreo por conglomerados se tiene que los elementos que pertenecen a la muestra son subconjuntos de la población, pero en este caso, a diferencia del muestreo estratificado, los elementos que pertenecen a cada subconjunto no necesariamente deben ser parecidos entre sí, pero sí se requiere saber cuales son los elementos que pertenecen al conglomerado Estratificado: Este tipo de muestreo no se considera un tipo de muestreo como tal, pero es muy importante por su uso en problemas cotidianos. Puede ver de la siguiente forma: se tiene una población que se divide en subconjuntos, con una estructura donde los elementos que componen cada conjunto son muy parecidos, pero los subconjuntos a su vez son diferentes entre sí, es decir son disyuntos. Luis Ernesto Leyva Camargo Muestreo no aleatorio Este tipo de muestreo se usa para indicar si existe un rasgo o característica particular en una población. Esta técnica de muestreo es ampliamente utilizada cuando los investigadores realizan investigaciones cualitativas, estudios piloto o investigación exploratoria. El muestreo no probabilístico se usa cuando los investigadores tienen un tiempo limitado para llevar a cabo la investigación o tienen limitaciones presupuestarias. El muestreo no probabilístico se realiza para observar si un tema en particular necesita un análisis en profundidad. Luis Ernesto Leyva Camargo Muestreo No aleatorio (no probabilístico) Muestreo no aleatorio Por conveniencia Luis Ernesto Leyva Camargo Subjetivo Bola de nieve Por cuotas Plan de muestreo y etapas de un estudio por muetreo 1. Definir los objetivos del problema a resolver. 2. Definir la población y las variables que se van a medir. 3. Hacer un presupuesto para garantizar que el estudio sea viable en términos de costos (tiempo, dinero) 4. Determinar el tipo de muestreo a utilizar. 5. Construir los instrumentos para recolectar los datos. 6. Recolección, procesamiento y difusión de la información obtenida. Teorema del límite central Luis Ernesto Leyva Camargo Teorema del límite central Si se toman muestras de lotes de datos de una población que tenga cualquier tipo de distribución y luego se toma la media de cada lote, la distribución de las medias será normal, independientemente del tipo de distribución que tenga la población subyacente. Aún si desconocemos la distribución de una muestra. Aplicando el teorema del límite central, podemos tratar la distribución de cualquier población como totalmente distribuida. E 𝑋ത ≈ 𝜇 𝜇𝑥ҧ ≈ 𝜇 𝜎2 V 𝑋ത ≈ 𝑛 𝜎 𝜎𝑥ҧ ≈ 𝑛 Luis Ernesto Leyva Camargo Gracias Luis Ernesto Leyva Camargo