REALTO HIDRAULICO

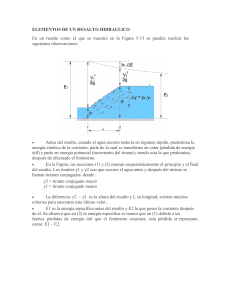
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 131
6. EL RESALTO HIDRÁULICO
6.1 OBJETIVOS
 Desarrollar la teoría básica del resalto hidráulico en canales abiertos, haciendo énfasis en las
características del resalto hidráulico en canales rectangulares de fondo horizontal.
 Generar y caracterizar determinado número de resaltos hidráulicos en un canal de laboratorio, de
sección rectangular y fondo horizontal.
 Validar las distintas formulaciones teóricas deducidas en el estudio de este fenómeno hidráulico.
6.2 FUNDAMENTOS TEÓRICOS
6.2.1 Introducción. El resalto hidráulico es el fenómeno que se genera cuando una corriente
supercrítica, es decir, rápida y poco profunda, cambia súbitamente a subcrítica, esto es, se vuelve
una corriente lenta y profunda. Este fenómeno es de central importancia en la Hidráulica de
Canales, por lo cual se trata aquí con suficiente amplitud.
Considérese el comportamiento del flujo en un canal de sección uniforme, cuya pendiente cambia
gradualmente de S01 < Sc a S02 > Sc , como se muestra en la Figura 6.1a.
FIGURA 6.1 Transiciones de régimen subcrítico a supercrítico debidos a cambios de pendiente.
Para un caudal constante y una sección transversal uniforme, la Línea de Profundidades Críticas,
L.P.C. es paralela al fondo del canal, y en la primera zona, en donde S 01 < Sc, el perfil de la
superficie libre queda por encima de dicha línea y la energía específica es mayor que la E mín . La
profundidad, y la energía específica disminuyen continuamente a medida que aumenta la pendiente
del canal y se alcanzan las condiciones críticas, esto es, en la sección en que la pendiente alcanza
un valor crítico, es decir, la pendiente crítica ( S0 = Sc ).
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
132
6. EL RESALTO HIDRÁULICO
La reducción que experimenta la energía específica en el canal, desde el valor inicial E 1 hasta Emín,
en la sección crítica, se disipa por el efecto de fricción y por pérdida de cabeza de posición. De la
sección crítica en adelante, la profundidad continúa disminuyendo con el aumento de la pendiente,
lo cual abastece de mayor energía al flujo, por aumento de velocidad, que la que se disipa por
fricción.
En el caso de una intersección brusca de dos pendientes, de subcrítica a supercrítica, el efecto
general es muy similar al del caso anterior, aunque es factible que el perfil de la superficie libre se
altere más en la zona de transición. Véase la Figura 6.1.b.
Aguas arriba de la intersección, la profundidad no puede, al menos teóricamente, ser menor que la
profundidad crítica, yc, ya que esto requeriría el suministro de energía desde el exterior, lo cual no es
posible, mientras no se alcance la pendiente pronunciada.
Por lo anterior, se concluye que la transición de régimen subcrítico a supercrítico es gradual,
acompañada de poca turbulencia y de pérdida de carga, debido, exclusivamente, a la fricción
durante el movimiento. Dicho proceso puede explicarse al recorrer la curva E vs. y, desde un punto
de la rama superior (subcrítica) a otro punto sobre la rama inferior de la misma curva (régimen
supercrítico).
Se considerará, ahora, el proceso inverso de transición de un régimen supercrítico a otro subcrítico:
En el numeral 4.2.4.3, se mostró que esta transición puede ocurrir, si se produce una reducción
local en el ancho del canal, seguida de una expansión. Sin embargo, dicha transición también puede
ocurrir si en el canal, de sección constante, hay un cambio en la pendiente, pasando de supercrítica
a subcrítica, tal como ocurre al pie de una rápida o caída (véase la Figura 6.2).
El régimen de flujo, aguas arriba de la intersección, es supercrítico, mientras que aguas abajo, la
pendiente impone un tirante normal en régimen subcrítico, presentándose, en algún punto
intermedio, la transición entre ambos.
FIGURA 6.2. Transición de régimen supercrítico a subcrítico.
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 133
Para explicar el proceso de transición se recurre a un análisis similar al anterior. El flujo, inicialmente
en régimen supercrítico, se frena por efecto de la fricción y de la reducción de la pendiente,
aumentando gradualmente su profundidad, y disminuyendo su energía específica, hasta alcanzar la
condición crítica (E = Emín). Como quiera que, aguas abajo, existe régimen subcrítico, la energía
específica del flujo debe ser menor que la E mín. Ello se debe a que la poca pendiente del canal no
abastece al flujo de energía adicional. Esto imposibilita la continuación de la explicación del
fenómeno, tal como se hizo en los casos anteriores.
Con el objeto de analizar la forma de la transición del régimen, se puede recurrir a la evidencia
experimental, la cual muestra que, al contrario de los casos anteriores, la transición de régimen
supercrítico a régimen subcrítico es en forma violenta y acompañada de mucha turbulencia y gran
“pérdida” de energía. En efecto, al entrar el agua a la zona de pendiente menor, se reduce la gran
velocidad del flujo, por efecto de la resistencia debida a la fricción, y se produce un incremento
brusco de la profundidad que, virtualmente, rompe el perfil del flujo, y produce un estado de gran
turbulencia y una fuerte pérdida de carga. A cierta distancia, aguas arriba del punto hipotético de
intersección del perfil de la superficie libre (que se va elevando ) con la Línea de Profundidades
Críticas, L.P.C., la energía específica está ya en exceso sobre aquella que corresponde a la del flujo
uniforme de aguas abajo; se produce, así, la discontinuidad y la superficie libre se eleva
rápidamente hasta la profundidad normal. A este fenómeno se le denomina Resalto Hidráulico, y
se muestra en las Figuras 6.2 y 6.3.
El resalto hidráulico ocurre con fuertes pulsaciones y como si el agua entrara en ebullición, indicio
irrefutable de la inclusión de aire. Después de un crecimiento irregular y brusco de la superficie libre
del agua, hasta alcanzar una profundidad igual a la normal, y n , en un tramo relativamente corto, el
frente turbulento se regulariza de manera inmediata, y continúa libremente en régimen subcrítico,
hacia aguas abajo.
La expansión turbulenta y la desaceleración del chorro de gran velocidad están asociadas con una
“pérdida” apreciable de energía, disipada ésta por calor, principalmente, y la energía específica final
es, precisamente, la correspondiente a la profundidad normal.
6.2.2 Ecuación general para el resalto hidráulico. Supóngase el resalto hidráulico formado en
un canal, como el que se muestra en la siguiente figura:
FIGURA 6.3. Fuerzas externas que actúan sobre un volumen de control a través de un resalto hidráulico.
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
134
6. EL RESALTO HIDRÁULICO
Al aplicar la ecuación de la cantidad de movimiento al volumen de control definido en la figura
anterior, resulta:

F
ext





ρ
v
β
v
d
A

s c
t

vc
ρ β v dvol
(6.1)
 es el coeficiente de Boussinesq, o coeficiente de corrección por momentum lineal.
Para flujos permanentes, el segundo término del miembro derecho de la ecuación (6.1) se anula; por
lo tanto, resulta:
F1  Wsen θ  Ff  Faire  F2 
  v 
s c1
1
1
v 1 dA 1  
  v 
2
s c2
2
v 2 dA 2 
(6.2)
cuyos términos se ilustran en la Figura 6.3.
 y1 A 1 cos   W sen θ  Ff  Faire   y 2 A 2 cos     v 1 1v 1A 1    v 2 2 v 2 A 2 
2
2
 y1 A1 cos   W sen θ  Ff  Faire   y 2 A 2 cos    ρ v1 β1 Q  ρ v 2 β 2 Q
2
2
2
2
 y1 A 1 cos   W sen θ  Ff  Faire   y 2 A 2 cos    ρ
2
 y 1 A1 cos  + W sen θ  Ff  Faire
Q
Q
β1 Q  ρ
β2 Q
A1
A2
2
β Q
β Q
  y 2 A 2 cos    ρ 1
 ρ 2
A1
A2
2
2
(6.3)
Reordenando términos correspondientes, se tiene:
β Q
 y 1 A 1 cos   ρ 1
A1
2
2
 W sen θ  Ff  Faire
β Q
  y 2 A 2 cos   ρ 2
A2
2
2
(6.4)
Dividiendo todos los términos de la ecuación (6.4) por  = g, resulta:
2
y 1 A 1 cos  
2
2
W sen θ  Ff  Faire
β1 Q
β Q
2

 y 2 A 2 cos   2
g A1
ρg
g A2
(6.5)
Definiendo M es la fuerza específica del flujo en una sección determinada, se tiene:
2
M1  y 1 A 1 cos  
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
2
β1 Q
g A1
(6.6)
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 135
y
M2
2
β Q
 y 2 A 2 cos   2
g A2
2
(6.7)
Con lo cual la ecuación (6.5) se transforma en:
M1 
W sen θ  Ff  Faire
ρg
 M2
(6.8)
6.2.3 Ecuación general para las profundidades conjugadas de un R.H. en canales
horizontales o de pendiente pequeña. Para canales horizontales o de pendiente pequeña
(  5º), sen   tan   0 y cos2   1.
Si, además, en la ecuación (6.8) se desprecian las fuerzas de resistencia con el aire y con las
fronteras sólidas de canal ( Faire = Ff = 0 ), resulta:
M1
 M2
(6.9)
Es decir,
y1 A 1 
β1 Q 2
g A1
 y2 A2 
β 2 Q2
gA2
(6.10)
Las profundidades y1 y y2 que satisfacen las ecuaciones (6.9) y (6.10) se llaman profundidades
conjugadas o secuentes del resalto hidráulico, y son las respectivas profundidades antes y
después del resalto hidráulico. Véase la Figura 6.4.
FIGURA 6.4. Resalto hidráulico y diagramas E vs. y y M vs. y, en canales de fondo horizontal.
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
136
6. EL RESALTO HIDRÁULICO
Reordenando términos, se tiene:
y 2 A 2  y1 A1
β1 Q 2 β 2 Q 2


g A1
gA2
(6.11)
Ahora, si 1 = 2 =  y factorizando el miembro derecho de la ecuación anterior, se tiene:
y 2 A 2  y1 A1
β Q2

g A1
 A1 
1 

A

2 
(6.12)
Ahora, multiplicando y dividiendo por A1 D1 el miembro derecho de la ecuación anterior, se tiene:
y 2 A 2  y1 A1
Q2
2
A1
 β
g D1

A 
 1  1  A 1 D1
A2 

A 
2 
y 2 A 2  y1 A1  β F1 1  1  A1 D1
 A2 
(6.13)
(6.14)
Análogamente, se llegaría al siguiente resultado:

2 A
y 2 A 2  y 1 A1  β F2  2  1 A 2 D2
 A1

(6.15)
Las ecuaciones (6.14) y (6.15) son las ecuaciones generales para las profundidades conjugadas de
un resalto hidráulico en canales horizontales o de pendiente pequeña.
6.2.3.1 Profundidades conjugadas de un resalto hidráulico en canales rectangulares de fondo
horizontal o de pendiente pequeña. Partiendo de la ecuación general (6.14), se tiene:
y 2 A 2  y1 A1
A 
2 
 β F1  1  1  A 1 D1
A2 

y2
y
2
B y 2  1 B y1  β F1
2
2
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
 B y1 
1 
 B y 1 y1
 By2 
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 137

1
2
2
B y 2  y1
2

2  y  y1 
 B y 12
 β F1  2
 y2 
2
1
y 2  y 1 y 2  y 1   β F12 y 2  y 1  y 1
2
y2
2
y2  y1 y2
2
2
 2 β F1 y 1
(6.16)
Dividiendo toda la ecuación por y12, resulta:
2
y2
y y
 1 22
2
y1
y1
2
F y
 2 β 1 21
y1
2
2
 y 2   y2 
      2 β F12
 y1   y1 
 0
(6.17)
La anterior es una ecuación cuadrática en (y2 / y1), cuya solución es:
 y2 
 
 y 1 1,2
 y2 
 
 y 1 1,2


1
1
12  4 1 2 β F12 
2 1
1  8 β F1
2
2
(6.18)
Descartando el signo negativo del radical de la ecuación anterior, se tiene:
y2
y1

y2
y1

1 
1  8 β F1
2
2
Finalmente,
1
2
 1  8 β F1  1


2
(6.19)
Análogamente, si se partiera de la ecuación general (6.15), se llegaría a la siguiente expresión:
y1
y2

1

2
2
1  8 β F2  1

UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
(6.20)
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
138
6. EL RESALTO HIDRÁULICO
Las ecuaciones (6.19) y (6.20) son las ecuaciones para las profundidades conjugadas del resalto
hidráulico en canales rectangulares de fondo horizontal o de pendiente pequeña.
6.2.4 Altura de un resalto hidráulico, hRH. Se define altura del resalto hidráulico a la diferencia
entre las profundidades conjugadas y2 y y1, Véase la Figura 6.4.
hRH
 y 2  y1
(6.21)
6.2.5 Tipos de resalto hidráulico. Los resaltos hidráulicos pueden ser de varios tipos, y suelen
clasificarse en atención a su ubicación respecto de su posición normal y al número de Froude F 1 .
6.2.5.1 Tipos de R.H., según su posición. Existen tres posibles posiciones del R.H. con respecto
a su fuente de generación (compuertas, vertederos de rebose y rápidas), mostradas en la Figura
6.5, dependiendo de la profundidad y’2, de aguas abajo, impuesta por algún control o por cualquier
condición particular del flujo.
FIGURA 6.5 Tipos de resalto hidráulico según su posición
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 139
6.2.5.1.1 Resalto hidráulico libre o en posición normal. Es la posición ideal de un R.H. para la
cual y1 y F1, inmediatamente aguas arriba del mismo, son tales que, al mismo tiempo que satisfacen
a la ecuación de las profundidades conjugadas (6.14) y (6.19), también se verifica que y 2 = y’2.
Véase la Figura 6.5 a.
6.2.5.1.2 Resalto hidráulico repelido. Es aquel resalto que se forma a una distancia, no
determinada teóricamente, aguas abajo de la posición normal descrita en el numeral anterior.
Ocurre porque la profundidad impuesta aguas abajo, y’ 2, es menor que y2, obtenida ésta de la
ecuación (6.14) o de la (6.19).
El R.H., en esta situación, se desplaza aguas abajo hasta una posición tal que y1 y F1, de la posición
normal, cambian a nuevos valores y’1 y F’1, tales que satisfacen, junto con y2 = y’2, a la ecuación de
las profundidades conjugadas (ecuaciones 6.14 y 6.19). Ver la Figura 6.5 b.
6.2.5.1.3 Resalto hidráulico sumergido o ahogado. Es la situación del R.H. que se desplaza
hacia aguas arriba, es decir, hacia la fuente generadora, en virtud de que la profundidad y’ 2, del
flujo, aguas abajo del resalto, es mayor que la profundidad y 2 que, junto con y1 y F1, satisfacen a la
ecuación de las profundidades conjugadas. Véase la Figura 6.5 c.
Los nuevos valores de y’1 y F’1, bajo la condición de R.H. ahogado, no son determinables
teóricamente.
6.2.5.2 Tipos de R.H., según el número de Froude, F1. La U.S. Bureau of Reclamation (Ref. [4])
ha clasificado los resaltos hidráulicos, en canales horizontales, de acuerdo al valor del número de
Froude, inmediatamente aguas arriba del resalto. Dicha clasificación se resume en la Tabla 6.1.
6.2.6 Longitud del resalto hidráulico, LRH. La longitud del R.H. se define como la distancia
comprendida entre la sección inmediatamente aguas arriba del resalto, fácilmente determinable, y
aquella sección de aguas abajo, en la cual se dejan de observar los rollos de agua en la superficie
libre. Véase la Figura 6.4. Esta última sección no es fácilmente apreciable, por lo que es esencial un
buen criterio, basado en la experiencia, para determinar la longitud de un resalto hidráulico.
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
140
6. EL RESALTO HIDRÁULICO
TABLA 6.1. Clasificación de los resaltos hidráulicos, según la U.S.B.R.
F1
Tipo de
Resalto
Hidráulico
Características del
Resalto Hidráulico
F1 < 1
No se forma
La corriente es subcrítica y
seguiría siendo subcrítica.
F1 = 1
El flujo es crítico y no se
No se forma presentan condiciones para la
formación de un R.H.
1 < F1  1.7
La superficie libre presenta
R.H. ondular ondulaciones. La disipación de
energía es baja, menor del 5%.
1.7< F1  2.5
R.H. débil
Se generan muchos rodillos de
agua en la superficie del resalto,
seguidos de una superficie suave
y estable, aguas abajo. La energía
disipada es del 5 al 15%.
R.H.
oscilante
Presenta un chorro intermitente,
sin ninguna periodicidad, que
parte desde el fondo y se
manifiesta hasta la superficie, y
retrocede nuevamente. Cada
oscilación produce una gran onda
que puede viajar largas distancias.
La disipación de energía es del 15
al 45%.
2.5 < F1  4.5
Esquema
Su acción y posición son poco
variables y presenta el mejor
4.5 <F1  9.0 R.H. estable comportamiento. La energía
disipada en este resalto puede
estar entre el 45 y el 70%.
F1 > 9.0
R.H. fuerte
Caracterizado
por
altas
velocidades y turbulencia, con
generación de ondas y formación
de una superficie tosca, aguas
abajo. Su acción es fuerte y de
alta disipación de energía, que
puede alcanzar hasta un 85%.
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 141
FIGURA 6.6 Curvas de variación LRH / y 2 vs. F1 para canales rectangulares horizontales e inclinados (Tomada de la referencia No. 3)
En uso de fundamentos teóricos, no es fácilmente determinable la longitud de los resaltos
hidráulicos; sin embargo, esta característica ha sido investigada experimentalmente por muchos
autores.
Particularmente, la U.S. Bureau of Reclamation (Ref. [4]), basándose en datos experimentales de
seis canales de laboratorio, preparó las curvas de variación L RH /y2 vs. F1, para canales
rectangulares horizontales e inclinados, mostradas en la Figura 6.6.
Por su parte, Silvester (1964) propuso las siguientes ecuaciones empíricas para el cálculo de la
longitud de resaltos hidráulicos en canales rectangulares, triangulares y parabólicos, en función del
número de Froude en la sección de agua arriba del resalto, F1, y de la profundidad inicial, y1:
Para canales rectangulares horizontales:
L RH
 9.75 y 1 F1  1 
1.01
(6.22)
Para canales triangulares simétricos, con un ángulo  = 47.3 º en el vértice:
L RH
 4.26 y 1 F1  1 
0.695
(6.23)
0.832
(6.24)
y para canales parabólicos, con F1  3.0:
L RH
 11.7 y 1 F1  1 
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
142
6. EL RESALTO HIDRÁULICO
6.2.7 Energía disipada en un resalto hidráulico, E. Como quiera que en un resalto hidráulico se
disipa parte de la energía específica que posee el flujo antes del fenómeno, se partirá de la
siguiente ecuación (véase la Figura 6.4):
E  E1 - E2
(6.25)
2
2

v1  
v2 




ΔE   y 1  1
   y 2  2 2 g 
2
g

 

(6.26)

1 Q 2  
2 Q2 




ΔE   y 1 
  y2 
2 
2 
2
g
A
2
g
A
1 
2 


Suponiendo que 1 = 2 = , se tiene:
  Q2
 Q 2 
ΔE  

 y 2  y 1
2
2 
2
g
A
2
g
A
1
2 


 1

 2  1 2   y 2  y 1
A
A 2 
 1

ΔE 
 Q2
2g
ΔE 
 Q2
2
2 g A1
2

A 
 1  1 2   y 2  y 1

A 2 

ΔE 
 Q2
2
2 g A1
2

A D 
 1  1 2   1   y 2  y 1

A 2   D1 

ΔE 
ΔE 
 Q2
2
1 A1
2 g D1
1
2
 F1
2

2

A 
 1  1 2  D1  y 2  y 1

A 2 

 A 12 
 1 2  D1  y 2  y 1 
 A 
2 



(6.27)
La ecuación (6.27) es la ecuación general para la energía disipada en resaltos hidráulicos, en
canales horizontales.
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 143
6.2.7.1 Energía disipada en un R.H., en canales rectangulares. Partiendo de la ecuación para
las profundidades conjugadas de un R.H., en un canal rectangular de fondo horizontal, se tiene:
y2
y1
1
2
 1  8 β F1  1

2

2
1
1  8βF
 y  
 2  2   1
  y1  
(6.19)
2
Por lo tanto,
2
2
F1
  y2  
2    1  1
 y1  
 
8β
(6.28)
Reemplazando este resultado en la ecuación general (6.27), se tiene:
2
ΔE 
  y2  
2    1  1
 B 2 y 12 
1   y1  
1 


 B 2 y 2  y 1  y 2  y 1 
2
8β
2 

(6.29)
ΔE 
2
y 2 y 2 
y 
 1   y2 
4    4  2   1  1  2 2 1  y 1  y 2  y 1
β 16   y 1 
  y 2
 y1 


ΔE 

 4 y2  y2
y
  1 y 2 2  y 12 12  y 2  y 1
β 16 y 1  y 1
y2

ΔE 
 1
β 4y2




 y 2  y1  2

 y 2  y12  y 2  y1
 y1 
(6.30)
Suponiendo  =  = 1, se tiene:

ΔE 
1
3
2
2
3
2
2
y 2  y1 y 2  y1 y 2  y 1  4 y1 y 2  4 y1 y 2
4 y1 y 2
ΔE 
1
3
2
2
3
y 2  3 y 2 y1  3 y 2 y1  y 1
4 y1 y 2

UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN


(6.31)
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
144
6. EL RESALTO HIDRÁULICO
Finalmente,
ΔE

y 2
 y1 
4 y1 y 2
3
(6.32)
La ecuación (6.32) es la ecuación para la energía disipada en un resalto hidráulico en canales
rectangulares y horizontales.
6.2.8 Eficiencia del resalto hidráulico, RH. Definiendo la eficiencia del R.H. como:
 RH 
E2
E1
(6.33)
y sabiendo que:
2
E1
 y 1  1
v1
2g
 y 1  1
2
E1

1 v 1
y1 
y1
2 g y1
2
v1  y1 
 
2 g  y 1 
2

1 1 v 1
y1 
y1
2 g y1
Por lo tanto,
E1 

y1
2
2  1 F1
2

E1
  2
 y 1  1  1 F1 
2


E2
v
 y 2  2 2
2g
(6.34)
Por otro lado,
2
(6.35)
De la ecuación de conservación de masa, se tiene:
Q  A1 v1
 A2 v2
Q  B y1 v1  B y 2 v 2
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 145
De donde,
y 
v 2   1  v 1
 y2 
(6.36)
Reemplazando (6.36) en (6.35), se tiene:
2
E2

 y  2
y 2  2  1  v 1
2 g  y2 
E2

y2 
E2
2 y 2   2 F1 y1

2
2y2
2

2
3
 2 v1  y1 
 2
2 g y 1  y 2 
3
2

2
 2 v1 y1
2 g y 22
y2 
y2 
 y1 
 
 y2 
3
 2 2  y1 
F1  2 
2
 y2 
3
(6.37)
Sustituyendo las ecuaciones (6.34) y (6.37) en la (6.33), se tiene:
3
ηRH

E2
E1


2 y 2   2 F1
η
RH

RH

2

y1
3
y2
2
2


2
2 y 2   2 F1 y 1
3
y1
y1 y 2
3
y1
2
1
1
2 y
3
2


3
  2 F1 y 1
2
2
y 1 y 2 2  1 F1
2

3
3
2   F 
2
3

y 1 2  1 F1
3
η
2
2 y 2   2 F1 y 1
2
2y2
y1
2
2   1 F1
2

y 
2
2  2    2 F1
 y1 
2
y2
2
2   1 F1
2
y1


3
ηRH

y 
2
2  2    2 F1
 y1 
2
 y2 
  2   1 F12
 y1 

UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN

(6.38)
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
146
6. EL RESALTO HIDRÁULICO
Además, de la ecuación (6.19), se tiene:
y2
y1

1

2
ηRH

1

2
2
2   1  8 β F1  1   2 F1


2

2
1 
2
2

 2  1  8 β F1  1 2  1 F1
ηRH
3
 1
2
2
2    1  8 β F1  1   2 F1

 8 

2
1
2
2
 1  8 β F1  1 2   1 F1

4
2
1  8 β F1  1

(6.19)
2
ηRH
ηRH






3
1
2
2
 1  8 β F1  1   2 F1

4
2
1
2
2
 1  8 β F1  1 2  1 F1

4


3


2
2
1  8 β F1  1  4  2 F1

2
2
2
2   1 F1  1  8 β F1  1




Suponiendo 1 = 2 =  = 1, y multiplicando y dividiendo por el conjugado del denominador, resulta:


 1  8F  1 3  4F 2 
1 


2
2
2
2  F1  1  8 F1  1


ηRH

ηRH

 
2
1  8 F1  1 

ηRH

 
2
4
2
1  8 F1  1 64 F1  4 F1 


2
4
2  F1 64 F1


2
 1  8 F 2  1
1


2
 1  8 F 2  1
1


(6.39)
2
2
2
2
2
1  8 F1  1  1  8 F1  1  4 F1 
 


2
2
2
2
2
2  F1  1  8 F1  1  1  8 F1  1

 


UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN



2
1  8 F1  1

2
1  8 F1  1

2
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
2
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 147
2 
4 F1 

ηRH

ηRH
2
16 F1 




2
2
ηRH
2  8 F1



2
2

2
2
2
2

2
1  8 F1 
2
2

1  8 F1  2
2
1  8 F1  1

2
1  8 F1  1

2
2
1  8 F1  4 F1  1

8 F1 2  F1


2
2
2
2


2  F 
2
2
1  8 F1 8 F1  1  4 F1  1



2
16 F1 2  F1
1  8 F1  4 F1 
2

2
8 F1 2  F1
8 F1
2
2
2
1  8 F1  1
2
1  8 F1  4 F1 
8 F1
2
2
1
1  8F  1  8 F   4 F
8 F 2  F 
2 12
ηRH

16 F1 2  F1
2
ηRH
2
1  8 F1  8 F1  2

ηRH
2
2
16 F1
2

16 F1 2  F1
8 F1

1  8 F1  16 F1  1  8 F1  2
16 F1
ηRH

2
2
2
1  8 F1  1   1  8 F1  1
 

2
2
16 F1 2  F1
2
ηRH

4
64 F1 2  F1
2
ηRH
2

2
1  8 F1  1 
 
2
4
1  8 F1  116 F1  


2
1
2
1
1
2
1
2
1
1
Finalmente, resulta:
ηR H
E2

E1
1  8F   4 F  1
8 F 2  F 
2 32

UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
2
1
1
2
1
2
(6.40)
1
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
148
6. EL RESALTO HIDRÁULICO
6.2.9 Altura relativa del resalto hidráulico en canales rectangulares. Es el cociente entre la
altura del R.H. y la energía específica del flujo, inmediatamente aguas arriba de éste, y se expresa
como:
hR H
E1

hR H
E1

hR H
E1

hRH
E1
hRH
E1


y 2  y1
v2
y1   1
2g
(6.41)
y 2  y1
2
v1  y1 
 
y1  
2 g  y 1 
y 2  y1
 2
y 1  F1 y 1
2
y

2  2  1
 y1

2
2   F1
 1
2 
2



y 2  y1
2
 v1
y1 
y1
2 g y1
y 2  y1
2
2 y 1   y 1 F1
2
1
2  
2 

2 y 2  y 1 
2
y 1 2   F1



2
1  8 β F1  1  1
 
2
2   F1
 1
2
1  8 β F1  2   1  2 1
2

2
2   F1
2
1  8 β F1  1  2
2
2   F1
Finalmente, resulta:
hR H
E1
2
1  8β F1  3

2   F1
2
(6.42)
Si     1, resulta:
hR H
E1
2
1  8F1  3

2  F1
2
(6.43)
6.2.10 Eficiencia de conversión de energía en un resalto hidráulico, en un canal rectangular
horizontal. En un R.H. se presenta un cambio de energía cinética en energía potencial, cuya
eficiencia de conversión se expresa como:
ηconv .R H

Ep
 Ek
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
(6.44)
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 149
η conv.R H

η conv.R H

m g y 2  m g y1
1
1
2
2
m v1  m  v 2
2
2
m g y 2  y 1 
  v 12  v 2 2 

m 


2
2


(6.45)

y 2  y1
2
2
v
v
 1  2
2g
2g
(6.46)
donde m representa la masa del fluido.
Por conservación de masa, se tiene:
v1 
y2
v2
y1
(6.47)
Reemplazando la ecuación (6.47) en la (6.46), se tiene:
η conv.R H

η conv.R H

η conv.R H

η conv.R H

y 2  y1
2
2
y  v 2
v
 2  2   2
2g
 y1  2 g
y 2  y1
2
2

v 2  y 2 
   1

2 g  y 1 


y 2  y1
2

v2 y2  y2

 2  1
2 g y 2  y1

2
(6.48)

y 2  y1


 v2
2
2 y2
y 2  y1
2
2 2gy2
y1
y 2  y 1  y 12
1
2
 F2 y 2  y 1 y 2  y 1  y 2
2
2
2

2 y1
2
 F2 y 1  y 2  y 2
(6.49)
De otro lado, de la ecuación (6.20) se tiene:
y1
y2

1
2
 1  8 β F2  1

2
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
150
6. EL RESALTO HIDRÁULICO
  y1  
2    1
  y2  
2

1  8 β F2
2
2
y
y
4 12  4 1  1  1
y2
y2
8β
F2
2
F2
2

4
8β
F2
2


1 1  y1    y1 
      1 
2 β  y2    y2 


 y  2  y 
 1    1 
 y 2   y 2 
(6.50)
Sustituyendo (6.50) en (6.49), se tiene:
2
η conv.R H
2 y1


η conv.R H

η conv.R H

1 y1
2β y2
 y1

  1 y 1  y 2  y 2
 y2

2 2 y 1 β
 y  y2
  1
 y2

 y 1  y 2 

4 β   y 1 y 2
y 1  y 2 2

4 β y1 y 2
 y 1  y 2 y 1  y 2 
(6.51)
Si  =  = 1, la ecuación anterior se vuelve:
η conv.R H

4 y1 y 2
y 1  y 2 2
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
(6.52)
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 151
6.2.11 Resalto hidráulico en canales rectangulares inclinados. Sea el resalto hidráulico formado
en un canal rectangular de fondo inclinado, como se muestra en la Figura 6.7.
FIGURA 6.7. Resalto hidráulico en un canal rectangular inclinado.
Cuando se analiza el fenómeno del R.H. en un canal de pendiente apreciable, debe incluirse la
componente del peso del volumen de agua, en el sentido del flujo. En canales horizontales o de
pendiente baja, esta componente es despreciable.
En atención al R.H. de la Figura 6.7, la ecuación de la cantidad de movimiento, en el sentido del
flujo, expresa lo siguiente:
F1  F2  W sen θ  Ff  Faire
 ρ Q β 2 v 2  β1 v 1 
 h1 A1   h2 A 2   volprisma  sen θ  Ff  Faire

(6.53)
 ρ Q β 2 v 2  β1 v 1 
d1 cos θ
B d1    d2 cos θ B d2     d1  d2  L B k senθ  Ff  Faire  ρ Q β 2 v 2  β1 v 1 
2
2
 2 
(6.54)
k: coeficiente de corrección por volumen del prisma de agua
Despreciando las fuerzas de fricción con el aire y con las paredes del canal, se tiene:
1
1
1
2
2
 B d1 cos θ   B d2 cos θ   d1  d2  L B k senθ  ρ Q  β 2 v 2  β1 v 1
2
2
2
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN

(6.55)
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
152
6. EL RESALTO HIDRÁULICO
Por conservación de masa:
Q  v 1 B d1
 v 2 B d2
(6.56)
de donde:
v2
d1
v1
d2

(6.57)
Reemplazando (6.56) y (6.57) en (6.55), resulta:
 d
1
1
1
2
2
 B cos θ d1   B cos θ d2  d1  d2   L B k senθ  ρ v 1 B d1  β 2 1 v 1  β1 v 1
2
2
2
 d2


 d
1
1
2
2
 B cos θ d1  d2   B d1  d2  L k senθ  ρ B v 1 d1 v 1  β 2 1  β1
2
2
 d2






Dividiendo por B, y si 1 = 2 = , resulta:



β v 12 d1  d1
1
1
2
2

cos θ d1  d2  d1  d2  senθ k L 
 1
2
2
g  d2

2
d

β v1
1
1
cos θ d1  d2 d1  d2   d1  d2  senθ k L 
d1  1  1 d1
2
2
g d1  d2

(6.58)
d2
1
1
2
cos θ d1  d2 d1  d2   d1  d2  senθ k L  β F1  d1  d2  1
2
2
d2
2
1
1  d1  d2 
2 d1
 sen θ k L  β F1
cos θ d1  d2   
2
2  d1  d2 
d2
1
1
d1  d2  senθ k L
cos θ d1  d 2 d1  d 2 
2
2

d1  d2 
d1  d2 
2
Ahora, multiplicando la ecuación (6.59) por d  d
1
2
cos θ d1  d 2  d1  d2  sen θ k L

d1  d2 
d1  d2 d1  d2
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
 β F1
(6.59)
2
d1
d2
2
, se tiene:

2 β F12 d12
d1  d2 d2
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 153
cos θ 
senθ k L
d1  d 2
 2 β F1
2
d12
d2 d1  d 2 
d 2 d1  d 2 
2 β F12

sen θ k L
d12
cos θ 
d1  d 2
d1 d 2 d 2 2
 2
d12
d1
d 2  d2 
 
d1  d1 

2
2 β F12
k L senθ
cos θ 
d 2  d1
2
F1
 2β
k L sen θ
cos θ 
d 2  d1
2
2
 d2   d2 
2 β F1
     
 d1   d1  cos θ  k L sen θ
d 2  d1
 0
(6.60)
Haciendo:
G1
G1
2
2

F1
k L sen θ
cos θ 
d 2  d1
(6.61)
F1
k L sen θ
cos θ 
d 2  d1

(6.62)
y reemplazando (6.61) en (6.60), resulta la siguiente ecuación cuadrática:
2
 d2   d2 
      2 β G12
 d1   d1 
 0
(6.63)
que, al resolverla, produce:
 d2 
 
 d1 1,2

1 
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
 12  4 1  2 β G12 
2 1
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
154
6. EL RESALTO HIDRÁULICO
 d2 
 
 d1 1,2
2

 1  1  8 β G1
2
Se ignora el signo (-) de la raíz, y resulta:
d2
d1
1 1
2
  
1  8 β G1
2 2
d2
d1

1
2
 1  8 β G1  1

2
L
Se cree que k y la relación d  d
2
1
G1 = f(F1, ).
(6.64)
dependen, principalmente, de F1.
(Ref. [4]).
Luego,
Como quiera que
d2  y 2 cos θ
y
d1  y 1 cos θ
entonces, reemplazando estas expresiones en (6.64), resulta:
y2
y1

1
2
 1  8 β G1  1

2
(6.65)
Dado que G1 = f (F1, ), las ecuaciones (6.64) y (6.65) evidencian que las relaciones d 2 /d1 y y2 /y1
son funciones de F1 y de .
En la Figura 6.8 se presentan las variaciones de y2 /y1 vs. F1 , y de d2 /d1 vs. F1, en función de la
pendiente del canal, S0.
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 155
FIGURA 6.8 Variaciones de y2 / y1 vs. F1 , y de d2 /d1 vs. F1, en función de la pendiente del canal, S0. (Tomada de la Ref. [3]).
6.3 PROCEDIMIENTO EXPERIMENTAL
6.3.1 Descripción de la instalación. La experimentación del resalto hidráulico se hará en el canal
horizontal, de acrílico, el cual está dotado de una compuerta plana, vertical y deslizante, en el
extremo de aguas arriba. En su extremo de aguas abajo está dotado de una compuerta tipo
persiana, con láminas de aluminio, las cuales se pueden girar a discreción. Véase la Figura 6.9.
Como se observa en la misma figura, una vez se abra la válvula de alimentación del canal, la
presencia de la compuerta deslizante obliga la formación de un flujo supercrítico aguas abajo de la
misma, dado que y1 < yc; al mismo tiempo, cerrando parcialmente la compuerta tipo persiana, se
promueve la formación de un flujo subcrítico, en el tramo compuerta - persiana. En consecuencia, el
estado transicional de los dos regímenes de flujo se manifiesta como un resalto hidráulico, cuyas
características se desean medir.
6.3.2 Datos y mediciones. Empleando los limnímetros situados en las secciones (1) y (2), se miden
las profundidades secuentes, y1 y y2, respectivamente, del resalto ya estabilizado. Al mismo
tiempo, aguas abajo se medirá la carga del vertedero de Bazin, h B, con la cual se calculará el
caudal, Q. Véase el montaje mostrado en la Figura 6.9.
Para el mismo resalto hidráulico formado, se medirá su longitud LRH, empleando una cinta de
flexómetro.
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
156
6. EL RESALTO HIDRÁULICO
FIGURA 6.9. Esquema de la instalación para la práctica de resalto hidráulico.
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 157
6.3.3 Cálculos y Resultados. Las restantes características del resalto hidráulico estudiado (h RH, F1,
F2, E1, E2, E, RH y tipo de resalto) se determinarán empleando las ecuaciones y clasificaciones ya
estudiadas. Estos resultados, junto con los datos obtenidos en el numeral anterior, se consignarán
en la Tabla 6.2.
Para caudales distintos, regulando la válvula de alimentación o regulando la abertura de la
compuerta, se generarán otros resaltos hidráulicos, cuyas características se medirán y calcularán
siguiendo el mismo procedimiento arriba descrito.
TABLA 6.2. Tabulación de datos experimentales para diversos resaltos hidráulicos
R. H. y1 y2 LRH
QB
E1 E2 Eexp Eteór
F1
F2
No. (m) (m) (mm) (m3/s) (adim) (adim) (m) (m) (m)
(m)
LRH
Tipo
y2,teór teór exp
conv
Gráfica
de
(m) (%) (%)
(%)
(m)
R. H.
1
2

n
6.4 CUESTIONARIO
6.4.1 ¿Qué relación se puede establecer entre F1 y hRH?
6.4.2 ¿Qué relación se puede establecer entre F1 y LRH?
6.4.3 ¿Qué relación se puede establecer entre hRH y E?
6.4.4 ¿Qué tan próximos son los valores de LRH medidos experimentalmente y LRH obtenidos de la
Figura 6.6?
6.4.5 ¿Qué tan similares son los valores de la profundidad secuente, y 2, obtenidos
experimentalmente, y los calculados con la ecuación de las profundidades conjugadas?
6.4.6 ¿Cómo son, comparativamente, los valores de RH, teórico y experimental?
6.4.7 ¿Cómo son, comparativamente, los valores de E, teórico y experimental?
6.4.8 ¿Qué se pudo observar, en relación a la posición del resalto ya estabilizado, cuando se abría
o cerraba la compuerta deslizante, y qué, cuando se abría o cerraba la compuerta tipo persiana?
6.4.9 ¿Qué se puede concluir acerca de los tipos de resalto y la energía disipada por ellos?
6.4.10 ¿Cuándo es necesario producir artificialmente un resalto hidráulico?
6.4.11 ¿En qué aplicaciones prácticas se podrá utilizar el resalto hidráulico?
6.4.12 ¿Qué tipo de problemas podría causar un resalto hidráulico en canales naturales y artificiales,
y cómo se podrían solucionar éstos?
6.4.13 Deduzca una ecuación para la estimación del error relativo total en la medición de la
eficiencia de un resalto hidráulico, RH.
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
Ramiro Marbello Pérez
Escuela de Geociencias y Medio Ambiente