resalto hidraulico

ECUACIÓN GENERAL DEL RESALTO HIDRÁULICO
Momentum del flujo en canales abiertos
En una sección de un canal, en la cual pasa un caudal Q con una velocidad V, la cantidad de
movimiento en la unidad de tiempo, se expresa por:
Cantidad de movimiento = β ⋅δ ⋅Q⋅V
Dónde:
β = Coeficiente de Boussinesq
V = Velocidad media
δ = densidad del fluido
Q = caudal
E
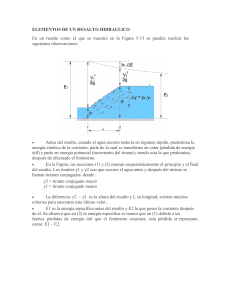
Considerando un tramo de un canal de sección transversal cualquiera donde se produce el
resalto hidráulico y tomamos el volumen de control limitado por las secciones (1) y (2), (antes y
después del resalto), por el piso del canal y por la superficie libre, como se muestra en la figura.
La variación de la cantidad de movimiento entre las secciones (1) y (2) será:
Variación de cantidad de movimiento =δ ⋅Q⋅ (β2 ⋅V2 – β1 ⋅V1)
De acuerdo con la segunda ley de Newton se tiene:
ΣF exteriores = cambio de cantidad de movimiento
ΣF exteriores = δ ⋅Q⋅ (β2 ⋅V2 – β1 ⋅V1)
Siendo:
∑ 𝐹 𝑒𝑥𝑡𝑒𝑟𝑖𝑜𝑟𝑒𝑠 = 𝐹𝑝1 − 𝐹𝑝2 + 𝑊. 𝑠𝑒𝑛𝛼 − 𝐹𝑓
Dónde:
𝐹𝑝1 , 𝐹𝑝2 = fuerza de presión actuando en las dos secciones.
W = peso del fluido (W·senα), peso del fluido en el sentido del movimiento.
𝐹𝑓 = fuerza externa total de resistencia que se opone al movimiento
Luego:
𝛿. 𝑄(𝛽2 . 𝑉2 − 𝛽1 . 𝑉1 ) = 𝐹𝑝1 − 𝐹𝑝2 + 𝑊. 𝑠𝑒𝑛𝛼 − 𝐹𝑓 … (1.1)
Fuerza especifica
Aplicando la ecuación (1), considerando que satisface las siguientes condiciones:
a) El canal es horizontal y de sección constante, pudiendo despreciarse la componente del
peso del fluido.
b) Se desprecia la resistencia de fricción originada en la pared del canal, debido a la poca
longitud del tramo en que se desarrolla el resalto.
c) Se considera que la distribución de velocidades en las secciones 1 y 2 de la figura, es
prácticamente uniforme y que los coeficientes:
β2 = β1 = 1
Volumen de control
Sección de control
Resulta:
𝛿. 𝑄(𝑉2 − 𝑉1 ) = 𝐹𝑝1 − 𝐹𝑝2
… (1.2)
Sustituyendo en (1.2) el valor de 𝑣 = 𝑄/𝐴, obtenido de la ecuación de continuidad, se tiene:
𝑄
𝑄
𝛿. 𝑄 ( − ) = 𝐹𝑝1 − 𝐹𝑝2
𝐴2 𝐴1
𝛿. 𝑄 2 (
1
1
− ) = 𝐹𝑝1 − 𝐹𝑝2 … (1.3)
𝐴2 𝐴1
Los empujes totales debidos a la presión hidrostática se pueden calcular como sigue:
𝐹𝑝1 = 𝛾𝑦̅𝐺1 𝐴1
𝐹𝑝2 = 𝛾𝑦̅𝐺2 𝐴2
Donde: 𝑦̅𝐺1 , 𝑦̅𝐺2 son las profundidades de los centros de gravedad de las áreas de las secciones
1y2
Sustituyendo estos valores en (1.3), resulta:
𝛿. 𝑄 2 (
1
1
− ) = 𝛾𝑦̅𝐺1 𝐴1 − 𝛾𝑦̅𝐺2 𝐴2
𝐴2 𝐴1
También:
𝛿. 𝑄 2
𝛿. 𝑄 2
+ 𝛾𝑦̅𝐺1 𝐴1 =
+ 𝛾𝑦̅𝐺2 𝐴2
𝐴1
𝐴2
Dividiendo entre 𝛾 = 𝛿. 𝑔, se tiene:
𝑄2
𝑄2
+ 𝑦̅𝐺1 𝐴1 =
+ 𝑦̅𝐺2 𝐴2 … (1.4)
𝑔𝐴1
𝑔𝐴2
La ecuación (1.4) proporciona en todos los casos, la solución de uno de los tirantes conjugados
a partir del otro conocido y representa la ecuación general del resalto hidráulico.
ECUACIONES DEL RESALTO HIDRÁULICO PARA
DIFERENTES FORMAS DE SECCIÓN
La ecuación general del resalto hidráulico y que proporciona la solución de uno de los tirantes
conjugados, para cualquier forma geométrica de la sección, conocido el otro es:
𝑄2
𝑄2
+ 𝑦̅𝐺1 𝐴1 =
+ 𝑦̅𝐺2 𝐴2
𝑔𝐴1
𝑔𝐴2
𝑜
𝑦̅𝐺2 𝐴2 − 𝑦̅𝐺1 𝐴1 −
𝑄 2 𝐴2 − 𝐴1
[
]=0
𝑔 𝐴1 𝐴2
De otro lado, cualquiera que sea la forma de la sección transversal, la profundidad 𝑦̅𝐺 de su
centro de gravedad se puede calcular con la ecuación:
𝑦̅𝐺 = 𝑘𝑦
Donde k es un coeficiente que depende de la geometría de la sección. Por lo tanto, la ecuación
anterior se puede escribir como sigue:
𝑘2 𝑦2 𝐴2 − 𝑘1 𝑦1 𝐴1 −
𝑄 2 𝐴2 − 𝐴1
[
] = 0 … . (1.8)
𝑔 𝐴1 𝐴2
A partir de la ecuación (1.8), a continuación, se desarrollan las ecuaciones particulares
Sección rectangular
Régimen supercrítico conocido
En una sección rectangular de ancho de solera b y tirante y, se tienen las siguientes relaciones
A= 𝑏𝑦
𝑘 = 1/2
Sustituyendo estos valores en la ecuación (1.8), se tiene:
1
𝑄 2 𝑏𝑦2 − 𝑏𝑦1
𝑦2 . 𝑏. 𝑦2 − 𝑘1 𝑦1 𝐴1 −
[
]=0
2
𝑔 𝑏𝑦1 . 𝑏𝑦2
𝑏𝑦2 2 𝑏𝑦1 2 𝑄 2 𝑦2 − 𝑦1
−
−
[
]=0
2
2
𝑔𝑏 𝑦1 𝑦2
𝑏
𝑄 2 𝑦2 − 𝑦1
(𝑦2 2 − 𝑦1 2 ) −
[
]=0
2
𝑔𝑏 𝑦1 𝑦2
𝑏
𝑄 2 𝑦2 − 𝑦1
(𝑦2 + 𝑦1 )(𝑦2 − 𝑦1 ) −
[
]=0
2
𝑔𝑏 𝑦1 𝑦2
Dividiendo entre
𝑦2 + 𝑦1 −
Pero:
𝑄
𝑏
𝑏(𝑦2 −𝑦1 )
2
, resulta:
2𝑄 2
=0
𝑔𝑏 2 𝑦2 𝑦1
= 𝑞 caudal unitario, luego:
𝑦2 + 𝑦1 −
2𝑞 2
= 0 … (1.9)
𝑔𝑦2 𝑦1
Multiplicando por 𝑦2 , se tiene:
𝑦2 2 + 𝑦2 𝑦1 −
2𝑞 2
=0
𝑔𝑦1
Aplicando la fórmula para hallar las raíces de la ecuación de 2° grado, se obtiene:
𝑦2 =
8𝑞 2
−𝑦1 ± √𝑦1 2 + 𝑔𝑦
1
2
,
𝑦2 =
−𝑦1
2𝑞 2 𝑦1 2
±√
+
2
𝑔𝑦1
4
Tomamos el signo (+)
𝑦2 =
−𝑦1
2𝑞 2 𝑦1 2
+√
+
… (1.10)
2
𝑔𝑦1
4
Ecuación que permite calcular el tirante conjugado mayor del resalto. En un canal de sección
rectangular, conocido el menor y el caudal por unidad de ancho.
Colocando la ecuación anterior en términos de la velocidad, ya que 𝑞1 = 𝑣1 𝑦1
𝑦2 =
−𝑦1
2𝑣1 2 𝑦1 2 𝑦1 2
+√
+
… (1.10)
2
𝑔𝑦1
4
,
𝑦2 =
−𝑦1
2𝑣1 2 𝑦1 𝑦1 2
+√
+
2
𝑔
4
… (1.11)
Sabemos que de la ecuación del número de Froude, se tiene:
𝐹1 =
𝑣1
√𝑔𝑦1
→ 𝐹1 2 =
𝑣1 2
𝑔𝑦1
Sustituyendo este valor en la ecuación (1.11), resulta:
𝑦2 =
−𝑦1
𝑦1 2
+ √2𝐹1 2 𝑦1 2 +
2
4
𝑦2 =
−𝑦1
𝑦1 2
+√
(8𝐹1 2 + 1)
2
4
𝑦2 =
−𝑦1 𝑦1
+ √8𝐹1 2 + 1
2
2
𝑦2 =
𝑦1
[√8𝐹1 2 + 1 − 1]
2
𝑦2 1
= [√8𝐹1 2 + 1 − 1] … (1.12)
𝑦1 2
Ecuación que permite calcular el tirante conjugado mayor del resalto, en un canal de sección
𝑣1
rectangular, conocido el menor y el número de Froude 𝐹1 = 𝑔𝑦
antes del resalto.
√
1
Régimen subcrítico conocido
𝑦1 =
−𝑦2
2𝑞 2 𝑦2 2
+√
+
… (1.13)
2
𝑔𝑦2
4
𝑦1 1
= [√8𝐹1 2 + 1 − 1] … (1.14)
𝑦2 2
Curva para determinar el tirante subcrítico, conocido el régimen supercrítico.
Curva para determinar el tirante supercrítico, conocido el régimen subcrítico
Sección Trapezoidal
Régimen supercrítico conocido
En una sección trapezoidal e ancho de solera b y taludes 𝑍1 y 𝑍2 , se tienen las relaciones:
𝐴 = 𝑏𝑦 + 𝑍𝑦 2
Donde:
𝑧=
𝑍1 + 𝑍2
2
Además:
𝐾=
1 1 𝑏
1 1 𝑏𝑦
+
= +
3 6 𝑏 + 𝑍𝑦 3 6 𝐴
De la ecuación (1.8), multiplicando por 𝐴2 , se tiene:
𝑘2 𝑦2 𝐴2 2 − 𝑘1 𝑦1 𝐴1 𝐴2 −
𝑄 2 𝐴2 − 𝐴1
[
]=0
𝑔
𝐴1
De la ecuación de continuidad, se tiene 𝑄 = 𝑣1 𝐴1 , luego:
𝑘2 𝑦2 𝐴2 2 − 𝑘1 𝑦1 𝐴1 𝐴2 −
𝑣1 2 𝐴1 2 𝐴2 − 𝐴1
[
]=0
𝑔
𝐴1
𝑘2 𝑦2 𝐴2 2 − 𝑘1 𝑦1 𝐴1 𝐴2 −
𝑣1 2 𝐴1
[𝐴2 − 𝐴1 ] = 0
𝑔
Dividiendo entre 𝑦1 , se tiene:
𝑦2 2
𝑣1 2 𝐴1
[𝐴2 − 𝐴1 ] = 0
𝑘2 𝐴2 − 𝑘1 𝐴1 𝐴2 −
𝑦1
𝑔𝑦1
Haciendo:
𝑟=
𝑣1 2
2𝑔
𝑦1
𝑣 2
1
= 2𝑔𝑦
,
1
Se tiene:
𝑘2
𝑦2 2
𝐴 − 𝑘1 𝐴1 𝐴2 − 2𝑟𝐴1 [𝐴2 − 𝐴1 ] = 0
𝑦1 2
Sustituyendo los valores de k, resulta:
1 1 𝑏𝑦2 𝑦2 2
1 1 𝑏𝑦1
( +
) 𝐴2 − ( +
)𝐴 𝐴 − 2𝑟𝐴1 [𝐴2 − 𝐴1 ] = 0
3 6 𝐴2 𝑦1
3 6 𝐴1 1 2
𝐴2 2 𝐴2 𝑏𝑦2 𝑦2
𝐴1 𝑏𝑦1
(
+
) −( +
)𝐴2 − 2𝑟𝐴1 [𝐴2 − 𝐴1 ] = 0
3
6
𝑦1
3
6
Sustituyendo los valores de A, se obtiene:
(𝑏𝑦2 + 𝑍𝑦2 2 )2 (𝑏𝑦2 + 𝑍𝑦2 2 )𝑏𝑦2 𝑦2
(𝑏𝑦1 + 𝑍𝑦1 2 ) 𝑏𝑦1
+
+
(
) −(
) (𝑏𝑦2 + 𝑍𝑦2 2 ) −
3
6
𝑦1
3
6
2𝑟(𝑏𝑦1 + 𝑍𝑦1 2 )[(𝑏𝑦2 + 𝑍𝑦2 2 ) − (𝑏𝑦1 + 𝑍𝑦1 2 )] = 0
3
Multiplicando por 𝑧2 𝑦 4 y ordenando en forma conveniente, se obtiene:
1
(𝑏𝑦1 + 𝑍𝑦1 2 ) 𝑏𝑦1
𝑏 𝑦2
𝑦2 2 (𝑏𝑦2 + 𝑍𝑦2 2 )𝑏𝑦2 𝑦2
[(
. + ( )2 ) +
] −(
+
) (𝑏𝑦2 + 𝑍𝑦2 2 ) −
𝑧𝑦1 𝑦1
𝑦1
6
𝑦1
3
6
2𝑟(𝑏𝑦1 + 𝑍𝑦1 2 )[(𝑏𝑦2 + 𝑍𝑦2 2 ) − (𝑏𝑦1 + 𝑍𝑦1 2 )] = 0
2
𝑏 𝑦2
𝑦2 2
1 𝑏 𝑏 𝑦2
𝑦2 2 𝑦2 𝑦2
. +( ) ] + .
[
. +( ) ] } −
{[
𝑧𝑦1 𝑦1
𝑦1
2 𝑧𝑦1 𝑧𝑦1 𝑦1
𝑦1
𝑦1 𝑦1
[
𝑏
1 𝑏
𝑏 𝑦2
𝑦2 2
+1+ .
. +( ) ]−
][
𝑧𝑦1
2 𝑧𝑦1 𝑧𝑦1 𝑦1
𝑦1
−6𝑟 [
𝑏
𝑏 𝑦2
𝑦2 2
𝑏
+ 1] {[(
. + ( ) )] − [
+ 1]} = 0
𝑧𝑦1
𝑧𝑦1 𝑦1
𝑦1
𝑧𝑦1
Haciendo los siguientes cambios de variables:
𝑏
= 𝑡;
𝑧𝑦1
𝑦2
=𝐽
𝑦1
Resulta:
1
{[𝑡𝐽 + 𝐽2 ]2 + . 𝑡[𝑡𝐽 + 𝐽2 ]𝐽} 𝐽 −
2
𝑡 𝑏 𝑦2
𝑦2 2
. +( ) ]−
[𝑡 + 1 + ] [
2 𝑧𝑦1 𝑦1
𝑦1
−6𝑟 [
𝑏
𝑏 𝑦2
𝑦2 2
𝑏
+ 1] {[(
. + ( ) )] − [
+ 1]} = 0
𝑧𝑦1
𝑧𝑦1 𝑦1
𝑦1
𝑧𝑦1
1
𝑡
[(𝑡𝐽 + 𝐽2 )2 + . 𝑡(𝑡𝐽 + 𝐽2 )𝐽] 𝐽 − (𝑡 + 1 + ) (𝑡𝐽 + 𝐽2 ) − 6𝑟(𝑡 + 1)[(𝑡𝐽 + 𝐽2 ) − (𝑡 + 1)] = 0
2
2
Efectuando, se tiene:
𝑡2 3 𝑡 4
3𝑡
3𝑡
𝐽 + 𝐽 − ( + 1) 𝑡𝐽 − ( + 1) 𝐽2 − 6𝑟(𝑡 + 1)𝑡 − 6𝑟(𝑡 + 1)𝐽2
2
2
2
2
+ 6𝑟(𝑡 + 1)2 = 0
𝑡 2 𝐽2 + 2𝑡𝐽4 + 𝐽5 +
Reduciendo términos semejantes, resulta:
5
3
3
3
𝐽5 + 𝑡𝐽4 + 𝑡 2 𝐽3 − [6𝑟(𝑡 + 1) + 𝑡 + 1] 𝐽2 − [6𝑟𝑡(𝑡 + 1) + ( 𝑡 + 1) 𝑡] 𝐽 + 6𝑟(𝑡 + 1)2 = 0
2
2
2
2
Factorizando el primer miembro, en términos de J, mediante el método de evaluación, luego
factorizando y ordenando en forma conveniente los coeficientes, resulta:
(𝐽 − 1) {𝐽4 +
5𝑡 + 2 3 (3𝑡 + 2)(𝑡 + 1) 2
𝑡2
𝐽 +
𝐽 + [ + (𝑡 − 6𝑟)(𝑡 + 1)] 𝐽 − 6𝑟(𝑡 + 1)2 } = 0
2
2
2
Dónde: 𝐽 − 1 ≠ 0, pues si 𝐽 − 1 = 0 → 𝐽 = 1,es decir
𝑦2
𝑦1
= 1, o también 𝑦2 = 𝑦1 , lo que indica
que los tirantes conjugados serian iguales, por lo tanto, no se produciría el resalto hidráulico.
Como 𝐽 − 1 =≠ 0, dividiendo la ecuación anterior entre (𝐽 − 1), se obtiene:
𝐽4 +
5𝑡 + 2 3 (3𝑡 + 2)(𝑡 + 1) 2
𝑡2
𝐽 +
𝐽 + [ + (𝑡 − 6𝑟)(𝑡 + 1)] 𝐽 − 6𝑟(𝑡 + 1)2 = 0 … (1.15)
2
2
2
La ecuación (1.15) es de cuarto grado, con la raíz real positiva, que permite calcular el tirante
conjugado mayor, conocidos:
a) El tirante conjugado menor, 𝑦1
𝑣 2
1
b) 𝑟 = 2𝑔𝑦
1
c) 𝑡 =
𝑏
𝑍𝑦1
Régimen subcrítico conocido
𝐽4 +
5𝑡 + 2 3 (3𝑡 + 2)(𝑡 + 1) 2
𝑡2
𝐽 +
𝐽 + [ + (𝑡 − 6𝑟)(𝑡 + 1)] 𝐽 − 6𝑟(𝑡 + 1)2 = 0 … (1.16)
2
2
2
Donde:
𝑦
𝑣 2
𝑏
2
a) 𝐽 = 𝑦1 ; 𝑟 = 2𝑔𝑦
; 𝑡 = 𝑍𝑦 ; 𝑍 =
2
2
2
𝑍1 +𝑍2
2
Curvas para el cálculo del tirante subcrítico conocido el régimen supercrítico en el
resalto hidráulico
Curvas para el cálculo del tirante supercrítico conocido el régimen subcrítico en el
resalto hidráulico