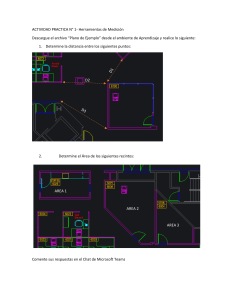
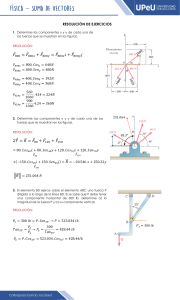
1. Se desea construir una piscina en el patio de una casa. Si la piscina tendrá forma de triángulo rectángulo y
uno de sus catetos es 4 m menor al otro cateto, ¿qué largo debe tener el cateto menor para que la
hipotenusa mida al menos 4√𝟓 𝒎?
a)
b)
c)
d)
𝑥
𝑥
𝑥
𝑥
≥8
>8
>4
≥4
2. De un grupo de 6 varones y 5 mujeres se va a elegir un comité de 5 personas que está integrado por 2
mujeres y 3 varones ¿Cuántos comités diferentes pueden ser elegidos?
a) 200
b) 20
c) 10
d) 30
3. La siguiente expresión relaciona el tiempo transcurrido (t) con la altura h(t) que alcanza el balón al ser
lanzado desde el suelo 𝒉(𝒕) = 𝟐𝟎𝒕 − 𝟏𝟎𝒕𝟐 . ¿Cuál es la máxima altura que alcanza el balón?
a)
b)
c)
d)
5𝑚
10 𝑚
20 𝑚
10√2𝑚
4. Si se escoge un número al azar en la guía telefónica de cierta ciudad ecuatoriana, la probabilidad de que
sea nombre de un hombre es 0,7 y de que figure una mujer es 0,3. En dicha ciudad, la probabilidad de que
un hombre trabaje es 0,8 y de que lo haga una mujer es 0,7. Se elige un número de teléfono al azar.
¿Cuál es la probabilidad de que corresponda a una persona que trabaja?
a)
b)
c)
d)
5.
a)
b)
c)
d)
0.77
0.56
0.21
0.47
Diez obreros demoran 8 días en hacer una obra, trabajando 6 horas diarias. ¿Cuánto demoran 24 obreros
trabajando 5 horas diarias, en hacer otra obra cuya dificultad es el cuádruple de la anterior?
8
24
16
10
6. El 32% de los asistentes a una reunión, eran hombres. Si el número de mujeres que asistió es 51.
Determine la cantidad de hombres que asistió a la reunión.
a) 24
b) 20
c) 22
d) 32
7. El lado de un cuadrado es 𝟑 𝒎 más largo que el de otro cuadrado y sus áreas difieren entre sí en 𝟒𝟓 𝒎𝟐 .
¿Cuánto mide el lado del cuadrado más grande?
a)
b)
c)
d)
3
6
9
12
~1~
8. A un congreso asisten 100 personas, de las cuales 65 son hombres y 35 son mujeres. Se sabe que el 10% de
los hombres y el 6% de las mujeres son especialistas en computación. Si se selecciona al azar a un
especialista en computación ¿Cuál es la probabilidad de que sea mujer?
a)
b)
c)
d)
0.65
0.35
0.06
0.244
9. En una colonia de abejas, en el primer día de investigación, alumnos de Ingeniería Agrícola contabilizaron
3 abejas, el segundo día habían 9, el tercero habían 15. ¿Cuántas abejas habían el último día del mes (en
este caso el mes tiene 30 días)?
a)
b)
c)
d)
174
180
177
190
10. Un arquitecto ofrece a una familia realizar un hermoso
diseño en el jardín de la parte posterior de su casa, que
cubrirá un área en forma de L de 15 m2, como se ve en la
imagen.
Determine la longitud del ancho del jardín si se sabe que el
terreno tiene su ancho uniforme. Todas las longitudes se
hallan en metros.
a)
b)
c)
d)
2.5 m
3.5 m
4m
7m
11. Por cada camiseta que compre el precio de costo es de $22, si al final compre 15 camisetas y me
descontaron el 20% por aniversario de la tienda y adicional por un sorteo me descontaron el 30%
adicional. ¿Qué porcentaje pague al final?
a)
b)
c)
d)
12.
50%
60%
56%
30%
Un escultor hará una representación en arcilla de una estrella,
para lo cual realiza un bosquejo, donde ∆𝑨𝑩𝑪 = ∆𝑨′𝑩′𝑪′;
ambos son equiláteros y el polígono que se forma es un
hexágono regular. Sin embargo, el escultor utiliza otro material
para el polígono, por lo tanto necesita determinar el área de
esa región. Sabiendo que la medida del segmento AB = 12 m.
Calcule el área del polígono.
a)
b)
c)
d)
4√3
6√3
24√3
36√3
~2~
13. En una mesa de billar, la bola azul se encuentra 50√𝟐 cm al sur de la amarilla y la esfera blanca se ubica a
40 cm en dirección sureste de la amarilla. Si las bolas blanca y azul, y la buchaca (agujero donde se dirigen
las bolas) se encuentran en línea recta, determina la posición de la esfera blanca respecto de la azul para
dirigir atinadamente el tiro.
a)
b)
c)
d)
−20√2𝑖 − 30√2𝑗
20√2𝑖 + 30√2𝑗
−30√2𝑖 − 20√2𝑗
−50√2𝑖 + 30√2𝑗
14. Una familia tiene un presupuesto mensual de $ 375 para hacer varias compras. Se realiza una compra de
un número X de kilos de frutas y verduras con un valor de $ 12, y un valor de Y kilos de carnes por $ 18. Si
la cantidad de kilos de carne es el triple que el de las frutas y verduras y se realizó un pago de $ 45 por
motivo de servicios básicos, ¿Cuántos kilos de frutas y verduras pueden comprar ese mes sin exceder el
presupuesto?
a)
b)
c)
d)
[0; 5.6]
[0; 5.0]
[0; 6.9]
[0; 6.0]
15. Para el ajuste de una pieza se ha utilizado una fuerza 𝑭𝑨 y 𝑭𝑩 , en
Newtons, como se muestra en la figura
Si para retirar la pieza se aplica una fuerza igual a 𝟓𝑭𝑨 − 𝟑𝑭𝑩. ¿Cuál es la
fuerza total que se ejerce en ese instante?
a)
b)
c)
d)
−19𝑖 − 16𝑗
−2𝑖 − 8𝑗
19𝑖 + 16𝑗
2𝑖 + 8𝑗
16. Un peón debe llevar una carretilla de arena al pie de cada uno de los 30 árboles que están a lado de una
calzada; los árboles están a 8 m de distancia y el montón de arena está a 10 m del primer árbol. ¿Cuánto
habrá recorrido después de haber terminado su trabajo y vuelto la carretilla al montón de arena?
a)
b)
c)
d)
8250 m
7560 m
5680 m
8200 m
17. En una panadería se producen 1500 panes. Si primero se venden 3/5 del total; luego, 5/6 del resto y se
queman 25 panes, ¿Cuántos panes quedan todavía?
a)
b)
c)
d)
100
75
500
200
~3~
18. Si en la figura adjunta, el radio de la circunferencia
circunscrita tiene 1 metro de longitud ABCDEF es un
̅̅̅̅ = 𝟑 y P, Q y R son los puntos medios
hexágono regular, 𝑷𝑸
𝟐
de 3 de los lados del hexágono; entonces, el área de la
superficie sombreada es:
a)
b)
5√3
6
15√3
16
4√3
c)
3
√3
d)
2
19. En el gráfico se muestran los tres puntos que se
establecieron para una carrera atlética: el de salida,
el de hidratación y el de llegada. Si un competidor
prepara su estrategia para el último tramo y tiene
20 minutos para completarlo: ¿Cuál es la velocidad
𝑲𝒎
en 𝒎𝒊𝒏 que debe mantener?
a)
b)
c)
d)
0.25𝑖 − 0.15𝑗
−0.25𝑖 + 0.15𝑗
0.25𝑖 − 0.25𝑗
−0.25𝑖 + 0.25𝑗
20. Para usar cierto cajero usted necesita un cierto código personal (CP).Cada CP en un alfabeto de 27 letras
está formado por 2 letras seguidas por un dígito del 0 al 9 (AT1 o CC3) o una letra seguida de dos dígitos
(P50 o J44). ¿Cuántos CP diferentes pueden ser asignados?
a) 10000
b) 11000
c) 9990
d) 10340
21. Al simplificar la expresión: (𝟐𝒙 − 𝟐−𝒙 )𝟐 + 𝟐 se obtiene:
a)
b)
c)
d)
22𝑥 + 2−2𝑥 + 2
22𝑥 − 2−2𝑥
22𝑥 + 2−2𝑥 − 2
22𝑥 + 2−2𝑥
22. En un laboratorio se lleva un registro del número de bacterias, en millones, que crecen en función del
𝟑
𝟑𝒕+𝟔
𝟐
tiempo para dos muestras diferentes. Si la primera muestra se encuentra expresada por (√𝟒)
𝟏 −𝟐𝒕−𝟑
mediante( )
,
𝟐
segunda
las muestras son iguales.
y la
donde t representa el tiempo en minutos, determine el tiempo en el que
~4~
a)
b)
3
7
8
21
c) −1
d)
5
21
23. La prueba final para ocupar la vacante de controlador aéreo en un
aeropuerto consiste en la interpretación del vector de vuelo de un
avión expresado en la figura. Si los radares proporcionados en esta
prueba utilizan coordenadas cartesianas, determine el vector que se
necesita para cumplir con la prueba correctamente.
a)
b)
c)
d)
28𝑖 + 28√3𝑗
−28𝑖 + 28√3𝑗
−28√3𝑖 + 28𝑗
28√3𝑖 − 28𝑗
24. Si 𝐥𝐨𝐠 𝟐 𝟑 = 𝒂 , ¿Cómo se puede expresar 𝐥𝐨𝐠 𝟏𝟖 𝟔?
a)
1+2𝑎
1−𝑎
b)
1+𝑎
1−𝑎
1−𝑎
c) 1+𝑎
1+𝑎
d) 1+2𝑎
25. El movimiento de un globo aerostático se modela por la función:
𝒕𝟐
𝒉(𝒕) = − + 𝟐𝒕 − 𝟏
𝟑
Donde la altura 𝒉(𝒕) se mide en kilometros y el tiempo 𝒕 en horas. Determine la máxima altura en
kilometros que alcanza el globo en su trayectoria.
a)
b)
c)
d)
2
3
4
5
26. En la figura adjunta el hexagono regular está inscrito en una
circunferencia, la cual está inscrita en un triángulo equilatero cuya
área de su superficie es igual a 𝟗√𝟑, entonces el área de la región
sombreada es:
3
a) 3 (2𝜋 − 2 √3)
b) 3(𝜋 − 3√3)
c) 4(2𝜋 − 3√3)
d)
3
(2𝜋
2
− 3√3)
~5~
27. Si 𝑨𝑩𝑪 es un triángulo equilátero inscrito en la circunferencia de
centro O, y además se conoce que el radio es 𝟏𝟔√𝟑 𝒄𝒎. Determinar
el perimetro del triángulo.
a) 54√3
b) 144
c) 36√3
d) 18
28. En la figura ABCD es cuadrado circunscrito a circunferencia de
centro O, e inscrito a otra circunferencia mayor concéntrica con la
̅̅̅̅ = 𝟖 𝒄𝒎, entonces el área
̅̅̅̅ = 𝑪𝑫
primera. En donde 𝑨𝑫
sombreada es:
a)
b)
c)
d)
8𝜋
8(𝜋 − 2)
8(𝜋 − 16)
16
29. Si 𝑨𝑩𝑪 es un triángulo equilátero inscrito en la circunferencia de centro
O, y además se conoce que el radio es 𝟏𝟎 𝒄𝒎. Determinar el área
sombreada.
a) 75√3
b)
100𝜋
3
− 75√3
c) 100𝜋 − 25√3
d)
100𝜋
3
− 25√3
30. Un atleta va a participar en una maratón y se desea saber que distancia es la que va a recorrer para poder
programar sus entrenamientos. Le informan que cuando haya recorrido 12 Km, le falta recorrer menos de
𝟑
𝟏
los de la longitud total; y si recorre 16 Km la distancia que le falta recorrer es mayor a de la longitud
𝟓
𝟓
total. Hallar la longitud, sabiendo que esta es el mayor entero posible.
a)
b)
c)
d)
19
22
38
29
~6~
31. Las acciones en la bolsa se cotizaron durante treinta
días de un mes en millones de dólares como se
muestra en la tabla.
Con base a la tabla obtuvo que la desviación
estándar es igual a 2 millones de dólares, además se
considera que la tendencia continúa el siguiente
mes. ¿En qué rango aproximado de millones de
dólares es 99,7% probable hallar la cotización de
acciones el próximo mes?
a)
b)
c)
d)
a)
b)
c)
d)
COTIZACIÓN DE
ACCIONES
(MILLONES DE DÓLARES)
𝑚𝑖
166
168
170
172
174
Total
DIAS
𝑓𝑖
10
10
8
1
1
30
𝑚𝑖 𝑓𝑖
1660
1680
1360
172
174
5046
1(162 − 174)
2(166 − 174)
3(174 − 172)
4(166 − 176)
32. De los vectores que aparecen en la figura, ¿Cuál es la magnitud
del vector resultante?
2 cm
3 cm
1 cm
4 cm
33. Una hormiga se desplaza erráticamente sobre una vereda. Un caminante curioso se detiene a estudiar su
movimiento y observa que durante algunos segundos realiza los siguientes movimientos sucesivos: 2 cm al
sur, 2 cm al este, 2 2 cm al noreste y finalmente 2 2 cm hacia al noroeste. Determine la magnitud del
desplazamiento total de la hormiga.
a) 2 cm
b) 4 cm
c) 2 2 cm
3 cm
d)
34. Determine el desplazamiento de la embarcación en coordenadas
geográficas, que necesita conocer el capitán para llegar a su
destino
a) 5; S 53° E
b) √7; S 53° E
c) 5; S 37° E
d) √7; S 37° E
35. Al lanzar tres monedas al aire, ¿Cuál es la probabilidad de que los
tres resultados sean iguales?
a)
b)
c)
d)
𝟏
𝟑
𝟏
𝟖
𝟏
𝟒
𝟏
𝟏𝟎
~7~
36. Una agencia de publicidad está pintando el logo de una empresa en
vallas, como se muestra en la figura. Si cada lado mide 4 m, ¿Cuál es el
área en 𝒎𝟐 , del logotipo?
a)
b)
c)
d)
4√3 − 2𝜋
√3 − 2𝜋
√3 − 4𝜋
2√3 − 2𝜋
37. Mario gasta un cuarto de su sueldo en vestimenta, de lo que sobra, un cuarto en alimentación. Si al final le
quedan USD 243. ¿Cuál era su sueldo originalmente?
a)
b)
c)
d)
675
918
432
189
38. En un videojuego de carreras, cada jugador debe elegir 2 personajes de un total de 5 posibles para que
sean el piloto y copiloto, respectivamente. Si 2 amigos se van a enfrentar en el videojuego, ¿de cuántas
maneras diferentes puede cada uno de ellos presentar los personajes en la carrera? Considere que todos
los personajes pueden ser elegidos por cada jugador en un orden determinado.
a)
b)
c)
d)
400
100
10
20
39. En una comunidad se construye un gran pozo de agua para almacenar el agua de lluvia. Este pozo se
construye en el piso y su forma es la de un prisma de base trapezoidal isósceles con una base mayor de 11
m, una base menor de 5 m y 4 m en cada lado. Además, para preservar el agua libre de contaminación se
debe colocar una tapa que coincida exactamente con los bordes del pozo. ¿Cuál es el área, en 𝒎𝟐 , de la
tapa requerida para cubrir el pozo?
a) 32
b) 44
c) 11√7
d) 8√7
𝟒
40. María tiene 𝟓 del dinero de Juan. Si María le da USD 14 a Juan, tendría
dinero, en dólares, Juan tenía al inicio?
a)
b)
c)
d)
35
28
49
14
~8~
𝟐
𝟕
del dinero de Juan. ¿Cuánto
41. Los ∆𝑨𝑩𝑪, ∆𝑨𝑫𝑩 𝒚 ∆𝑫𝑪𝑬 son equiláteros,
determine el área de la región sombreada
si
̅̅̅̅ = 𝟔,
𝑨𝑫
a) 18√3
b) 20
c) 6√5
d) 3√3
42. En el proyecto METRO – QUITO – ODEBRECTH, se descubrió que un sistema informático tiene periodos de
error, dados por la expresión:
𝐥𝐨𝐠 𝟐(𝒕𝟐 + 𝟐) = 𝐥𝐨𝐠 𝟐 𝟑𝒕 + 𝐥𝐨𝐠 𝟐 (𝒕 − 𝟏)
Donde t está dada en horas. Encuentre en cuantas horas se produce los periodos de error.
a)
b)
c)
d)
3
2
4
5
43. Una persona pretende obtener el modelo matemático de un circuito electrónico en serie con resistencia
constante. Cuando alimenta el circuito con un voltaje de 9 V, mide que la corriente que circula es 2 A,
mientras que, cuando alimenta el circuito con una fuente constante de 12 V, la corriente es 2,75 A. Si
luego de otras mediciones se logra establecer que la relación entre la corriente y el voltaje es lineal,
determine la variación de corriente por cada voltio de la fuente para que la persona pueda definir el
modelo matemático del circuito.
a) 4
1
b) 4
c) −4
1
d) − 4
44. Una familia tiene un presupuesto mensual de $ 394 para hacer varias compras. Se realiza una compra de
un número X de kilos de frutas y verduras con un valor de $ 12, y un valor de Y kilos de carnes por $ 54. Si
la cantidad de kilos de carne es el triple que el de las frutas y verduras y se realizó un pago de $ 46 por
motivo de servicios básicos, ¿Cuántos kilos de frutas y verduras pueden comprar ese mes sin exceder el
presupuesto?
a)
b)
c)
d)
[0; 3.86]
[0; 2.0]
[0; 2.26]
[0; 4.37]
~9~
45. En una granja se adquieren 120 kg de comida para alimentar a 20 animales de corral durante 4 días. Si se
duplica la cantidad de animales en la granja y se compra 60 kg adicionales de comida. ¿Cuántos días
durará el alimento?
a)
b)
c)
d)
16
12
7
3
46. Un hospital realiza un estudio sobre las edades de las personas que se hicieron estudios de sangre en un
mes, obteniendo la tabla mostrada:
Edad del
Marca de
Frecuencia
𝒙𝒊 𝒇𝒊
𝒙𝒊 𝟐 𝒇𝒊
paciente
clase (𝒙𝒊 )
(𝒇𝒊 )
[𝟓; 𝟏𝟓)
10
8
80
800
[𝟏𝟓; 𝟐𝟓)
20
10
200
4000
[𝟐𝟓; 𝟑𝟓)
30
12
360
10800
[𝟑𝟓; 𝟒𝟓)
40
10
400
16000
TOTAL
40
1040
31600
Determine el valor de la desviación estándar de los pacientes atendidos este mes, que servirá para
determinar las áreas que necesitan mayor apoyo de su personal.
a)
b)
c)
d)
1466
√114
114
√1466
47. Un disco de mp3 contiene 100, 150 y 50 canciones diferentes de rock clásico, salsa y merengue
respectivamente. Si el disco se reproduce aleatoriamente en un equipo de sonido donde las canciones no
se pueden repetir, determine la probabilidad de que las 2 primeras canciones que toque el equipo sean
canciones de rock clásico.
a)
b)
c)
d)
33
299
1
50
1
3
11
100
48. Una empresa dedicada a la comercialización de herramientas desea introducir un nuevo producto al
mercado. Con este objetivo, aplicó una encuesta que servirá para fijar el precio de la nueva herramienta.
El estudio determinó que con un precio de USD 16 hay 2250 personas interesadas en comprar la nueva
herramienta, mientras que con un precio de USD 17, hay 1500 personas interesadas. Si la relación entre
el número de clientes y el precio establecido es lineal, ¿Cuál es el intervalo absoluto de los precios que se
le puede asignar a la nueva herramienta?
a)
b)
c)
d)
]0; 19[
[16; 19[
[17; 19[
[16; 17]
~10~
49. Una empresa de ropa deportiva divide la cantidad de productos en un 60% de camisetas, un 30% de
pantalones y un 10% de zapatos. Además, el departamento de manufactura ha delimitado que los
artículos defectuosos producidos son el 10%, 5% y 5% de cada artículo, respectivamente. Si un cliente
compró un artículo de esta empresa y resultó defectuoso. ¿Cuál es la probabilidad de que haya sido un
pantalón?
a)
b)
c)
d)
19
184
57
184
3
16
1
16
50. Una profesora lleva el registro de calificaciones de sus estudiantes en su computadora, pero por error
perdió las calificaciones de María y solo dispone del promedio de las 3 asignaturas que toma, que es 18
puntos. Además, recuerda que María obtuvo en Física 4 puntos menos que en Cálculo, y en Química 1
punto más que en Cálculo. Determine la nota que María obtuvo en Física y que permitirá a la profesora
completar el registro.
a)
b)
c)
d)
51.
15
20
17
19
Una tienda de equipos electrónicos está rematando su mercadería por fin de temporada. Se conoce que la
tienda dispone de 80 equipos en total. El 45% de los equipos es vendido en USD 80 cada uno; el 75 % de lo
restante en USD 90, y los últimos equipos en USD 100. Determine la ganancia, en dólares, que obtendrá
luego de vender todos los equipos.
a)
b)
c)
d)
7170
7080
6950
6980
52. La ganancia de una granja, en función de la cantidad de conejos, se puede representar mediante la
fórmula:
𝑮(𝒄) = 𝟐𝒍𝒐𝒈𝒄 − 𝐥𝐨𝐠(𝒄 + 𝟔)
Donde
G: ganancia
C: número de conejos
a)
b)
c)
d)
Con base en los datos, ¿Cuántos conejos había cuando la ganancia era cero?
2
6
1
3
53. La magnitud de un movimiento telúrico (sismo) tiene una relación con el logaritmo de la energía liberada
durante el evento como indica la fórmula:
𝒍𝒐𝒈𝟏𝟎 𝑬𝒏𝒆𝒓𝒈𝒊𝒂 𝒍𝒊𝒃𝒆𝒓𝒂𝒅𝒂 = 𝑴𝒂𝒈𝒏𝒊𝒕𝒖𝒅 𝒅𝒆𝒍 𝒎𝒐𝒗𝒊𝒎𝒊𝒆𝒏𝒕𝒐 𝒕𝒆𝒍ú𝒓𝒊𝒄𝒐
~11~
Si un primer movimiento tiene una magnitud de 10 grados en la escala de Richter y una de las réplicas de
5 grados en la escala de Richter. ¿Cuántas veces es mayor la energía inicial liberada con respecto a la
segunda?
a)
b)
c)
d)
2
105
5
102
54. Complete el enunciado
En una cámara de climatización en la que se investiga el crecimiento de una variedad de plantas, la
temperatura es regulada mediante una función 𝒇(𝒕) que depende del tiempo t en horas.
𝒇(𝒕) = −(𝒕 − 𝟑)𝟐 + 𝟗
Considerando que las temperaturas deben ser mayores a 𝟎° 𝑪, se necesita definir los intervalos de tiempo en
el cual se alcanza la temperatura más alta para la toma de mediciones, por lo que se determina que para el
dominio de ___la función tiene una monotonía___
a)
b)
c)
d)
55.
a)
b)
c)
d)
(0; 6) − 𝑐𝑟𝑒𝑐𝑖𝑒𝑛𝑡𝑒
(0; 6) − 𝑑𝑒𝑐𝑟𝑒𝑐𝑖𝑒𝑛𝑡𝑒
(0; 3) − 𝑑𝑒𝑐𝑟𝑒𝑐𝑖𝑒𝑛𝑡𝑒
(0; 3) − 𝑐𝑟𝑒𝑐𝑖𝑒𝑛𝑡𝑒
Un agricultor debe sembrar maíz, plátano, cacao y café en partes iguales. Se dispone de un terreno
cuadrado, cuyo perímetro mide 16 m, determine el área en 𝒎𝟐 , que se ocupará para la siembra de maíz.
12
8
16
4
56. Para realizar el cultivo de papas, 3 hermanos han decidido dividir el terreno total de manera directamente
proporcional a sus edades, así desde el menor al mayor, se tiene las relaciones de 2, 4, 6. Si el terreno total
es de 𝟏𝟐𝟎 𝒎𝟐 , determine los 𝒎𝟐 que le corresponderá cultivar al menor de los hermanos.
a)
b)
c)
d)
10
60
20
30
57. Las estadísticas de los resultados de un equipo profesional de fútbol se pueden resumir en la tabla
Condición
Local
Visitante
Partidos
Ganados
34
18
Partidos
Perdidos
15
20
Sabiendo que el próximo partido juega de local, ¿Cuál es la probabilidad que el equipo gane el encuentro?
a)
b)
c)
d)
34
49
52
87
49
87
34
52
~12~
58. Sandra acude a un almacén de calzado y compra un par de zapatos que se encontraba con el 50% de
descuento del precio marcado en la etiqueta, sin incluir el IVA. Si el predio final que Sandra pagó por los
zapatos, incluido el IVA del 10%, es de USD 55, ¿Cuál era el precio, en dólares, marcado en la etiqueta?
Aproxime su respuesta al entero más cercano.
a)
b)
c)
d)
28
110
92
100
59. Lo que cobra y gasta un profesor suman 600. Lo que gasta y lo que cobra están en relación de 2 a 3. ¿En
cuánto tiene que disminuir el gasto para que dicha relación sea de 3 a 5?
a) 16
b) 15
c) 24
d) 32
60. El sueldo de Luis es al sueldo de Julio como 5 es a 3. Cierto mes por equivocación Julio recibió $720 más,
con lo cual recibió la misma cantidad que Luis. ¿Cuánto es el sueldo de Luis?
a) 1080
b) 1700
c) 1800
d) 1200
61. La suma de los 4 términos de una proporción es 65, cada uno de los 3 últimos términos es los 2/3 del
anterior. ¿Cuál es el último término?
a) 8
b) 7
c) 10
d) 12
62. Se diseña un túnel de 𝟒𝒎 de ancho y 𝟒𝒎 de alto como se muestra en la
figura. Determine la ecuación que se deberá utilizar para el diseño del
túnel.
a)
b)
c)
d)
−𝑥 2 + 2𝑥 + 3
−𝑥 2 + 2𝑥 − 3
𝑥 2 + 2𝑥 + 3
−𝑥 2 − 2𝑥 + 3
63. Una torre en estructura metálica está sometida, a las fuerzas, en
Newtons, que se indican en la figura, donde cada cuadrícula
corresponde a 10 newtons.
Determine la fuerza 𝑭𝒆 , en Newtons, que deberá adicionarse para
que la estructura esté en equilibrio (sumatoria de fuerzas igual a
cero) ya que los elementos requieren estabilidad.
a)
b)
c)
d)
−50𝑖 − 70𝑗
50𝑖 + 70𝑗
−110𝑖 − 10𝑗
110𝑖 + 10𝑗
~13~
64. En una granja se adquieren 𝟏𝟐𝟎𝑲𝒈 de comida para alimentar 20 animales de corral durante 4 días. Si se
duplica la cantidad de animales y se compra 𝟔𝟎 𝑲𝒈 adicionales de comida. ¿Cuántos días durara el
alimento?
a) 16
b) 12
c) 7
d) 3
65. La figura muestra tres fuerzas que actúan sobre un cuerpo situado en el
origen de coordenadas. Calcular el ángulo 𝜽 si la fuerza resultante es
nula.
a)
b)
c)
d)
30°
60°
45°
120°
66. Cinco amigas, ¿De cuántas maneras diferentes podrán hacer cola para comprar pan, si Claudia estará
siempre adelante y Andrea siempre estará última?
a) 24
b) 6
c) 10
d) 12
67. La relación de ángulos agudos de un triángulo rectángulo es como 2 es a 3. ¿Cuál es el mayor de estos
ángulos?
a) 36°
b) 48°
c) 54°
d) 62°
68. Los perímetros de un cuadrado y un triángulo equilátero, son iguales. Entonces el área del triángulo es al
área del cuadrado como:
a)
b)
c)
d)
9√3
4
4√3
9
3√3
4
9√3
8
69 En un campamento vacacional el logotipo para diferenciar los distintos
grupos en un triángulo equilátero inscrito en un círculo de 5 cm de radio,
como se muestra en la figura. Si se sabe que la relación entre el área del
triángulo y el área del círculo es
𝟐
𝟑√𝟑
,
𝟒𝝅
determine el área del triángulo, en
𝒄𝒎 para comprar las pinturas necesarias para cada grupo.
a)
b)
c)
d)
15√3
4
75√3
4
75√3
2
15√3
2
~14~
70.
a)
b)
c)
d)
Un reloj da el número de campanadas de la hora correspondiente. ¿Cuántas campanadas da un día?
24
48
78
156
71. De cierta población se sabe que el 50% fuma, el 10% fuma y es hipertensa. ¿Cuál es la probabilidad de que
un fumador sea hipertenso?
a) 0.15
b) 0.2
c) 0.8
d) 0.4
72. En la biblioteca del señor Valdez, las tres cuartas partes de los libros son de Medicina, la quinta parte del
resto son de Biología y completan la colección 20 libros de Historia. ¿Cuántos libros de Medicina y Biología
tiene?
a) 5 de Medicina y 75 de Biología
b) 300de Medicina y 80 de Biología
c) 80 de Medicina y 300 de Biología
d) 75 de Medicina y 5 de Biología
73. Las mediciones de voltaje, en voltios, y de corriente eléctrica, en amperios, para un circuito eléctrico en
serie se han medido así: cuando el voltaje de entrada es 8 V, la corriente medida es 4 A; mientras que
para un voltaje de 24 V de entrada, la corriente es 8 A. Si después del estudio matemático del circuito se
establece que la relación de la corriente que depende del voltaje de entrada es lineal, determine la
función que permite conocer la intensidad de corriente I, dependiendo del voltaje de entrada V.
V
a)
−2
4
b) 4V − 28
V
c) 4 + 2
d) 4V + 28
74. Dos máquinas A y B han producido respectivamente 100 y 200 piezas. Se sabe que A y B producen un 5% y
6% de piezas defectuosos respectivamente. Si se toma una pieza cualquiera y es defectuosa, ¿Cuál es la
probabilidad de que proceda de la primera máquina?
𝟐
a) 𝟏𝟕
b)
c)
d)
𝟏𝟓
𝟏𝟕
𝟓
𝟏𝟕
𝟑
𝟏𝟕
75. Con base en el texto, identifica el sistema de restricciones que se ajusta a este modelo de programación
lineal de maximización en la fabricación de cada modelo de refrigeradora.
Una empresa produce dos tipos de refrigeradoras tipo A especial y tipo B general. La primera necesita 10
horas de trabajo para su fabricación y 4 para los acabados, mientras que la segunda requiere 9 horas en su
fabricación y 2 en los acabados. Se dispone como máximo de 180 horas de trabajo en fabricación y 45 en
los acabados por semana.
4x + 9y ≤ 180
10𝑥 + 2𝑦 ≤ 45
a) {
𝑥≥0
𝑦≥0
~15~
4x + 10y ≤ 45
9𝑥 + 2𝑦 ≤ 180
b) {
𝑥≥0
𝑦≥0
10x + 2y ≤ 45
4𝑥 + 9𝑦 ≤ 180
c) {
𝑥≥0
𝑦≥0
10x + 9y ≤ 180
4𝑥 + 2𝑦 ≤ 45
d) {
𝑥≥0
𝑦≥0
76. Para conformar una microempresa, tres socios aportan con un capital inicial: el primero USD 250, el
segundo USD 300 y el tercero USD 450. Después de un tiempo obtienen una ganancia total de USD 3000
que debe ser distribuida entre los socios proporcionalmente a su inversión inicial. Determine la cantidad,
en dólares, que le corresponde al segundo socio.
a)
b)
c)
d)
750
900
1000
1350
77. Una empresa de quesos desea introducir un nuevo producto al mercado. Con este objetivo, realizó una
encuesta que servirá para fijar el precio de la nueva variedad de quesos, que determinó que con un precio
de USD 3 hay 4500 personas interesadas en comprar el producto, mientras que, con un precio de USD 5,
hay 3000 personas interesadas. Si la relación entre el número de clientes y el precio establecido es lineal.
¿Cuál es el intervalo de precios que se le puede asignar a cada queso?
a)
b)
c)
d)
]0,9[
]3,5[
]5,7[
]9, 11[
78. En un videojuego de carreras, cada jugador debe elegir 3 personajes de un total de 7 posibles para que
sean el piloto y copiloto, respectivamente. Si 2 amigos se van a enfrentar en el videojuego, ¿de cuántas
maneras diferentes puede cada uno de ellos presentar los personajes en la carrera? Considere que todos
los personajes que pueden ser elegidos por cada jugador sigue un orden específico.
a) 35
b) 210
c) 1225
d) 44100
79. Alejandra debe pagar su préstamo en 14 cuotas que aumentan USD 5 cada mes. Si la cuota inicial es de
USD 7, ¿cuánto pagará en total?
a) 158
b) 486
c) 553
d) 609
80. Complete el enunciado.
Según reglamentos internos de las universidades, el estudiante que no registre al menos un 80 % de
asistencia reprobará la asignatura. La tabla muestra el registro de las asistencias a clases de Agustín en el
último semestre en sus cuatro asignaturas.
~16~
Asignatura
Álgebra
Física
Matemática
Química
Asistencia
23 de 28
16 de 20
21 de 26
19 de 24
Agustín reprobó _______ por inasistencia.
a)
b)
c)
d)
Álgebra
Física
Matemática
Química
81. En el aula de una universidad el 70 % de estudiantes son mujeres y el 5 % de ellas han repetido una o
varias materias, además el 15 % de los estudiantes hombres también han pasado por esto. Si al realizar un
estudio socioeconómico se elige un estudiante entre los que han repetido materias, ¿cuál es la
probabilidad de que el estudiante sea hombre?
9
a)
200
b)
c)
d)
9
16
7
20
79
20
82. En una cesta se colocan manzanas y peras. Si una persona desea tomar las dos frutas, la probabilidad es de
𝟒
𝟏𝟐
, y si desea escoger una pera, la probabilidad es de . ¿Cuál es la probabilidad de que habiendo
𝟏𝟕
𝟏𝟖
extraído una pera, luego escoja una manzana?
8
a) 51
b)
c)
d)
6
18
6
17
22
51
83.
~17~