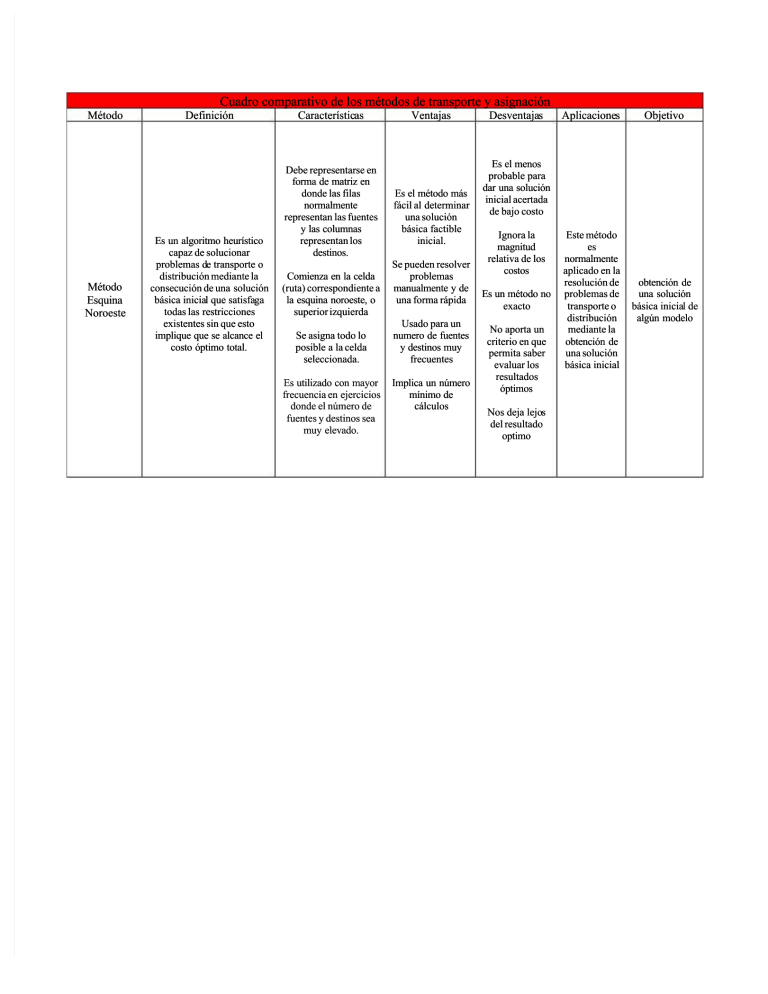
Cuadro comparativo de los métodos de transporte y asignación Método Método Esquina Noroeste Definición Es un algoritmo heurístico capaz de solucionar problemas de de transporte o distribución mediante la consecución de una solución básica inicial inicial que satisfaga satisfaga todas las restricciones existentes sin que esto implique que se alcance el costo óptimo total. Características Características Debe representarse en forma de matriz en donde las filas normalmente representan las fuentes y las columnas representan los destinos. Comienza en la celda (ruta) correspondiente a la esquina noroeste, o superior izquierda Se asigna todo lo posible a la celda seleccionada. Es utilizado con mayor frecuencia en ejercicios donde el número de fuentes y destinos sea muy elevado. Ventajas Es el método más fácil al determinar una solución básica factible inicial. Se pueden resolver problemas manualmente y de una forma rápida Usado para un numero de fuentes y destinos muy frecuentes Implica un número mínimo de cálculos Desventajas Desventajas Aplicaciones Aplicaciones Objetivo Este método es normalmente aplicado en la resolución de problemas de transporte o distribución mediante la obtención de una solución básica inicial obtención de una solución básica inicial inicial de algún modelo Es el menos probable para dar una solución inicial acertada de bajo costo Ignora la magnitud relativa de los costos Es un método no exacto No aporta un criterio en que permita saber evaluar los resultados óptimos Nos deja lejos lejos del resultado optimo Cuadro comparativo de los métodos de transporte y asignación Método Método Aproximación de Vogel Definición Es un método heurístico de resolución de problemas de transporte capaz de alcanzar una solución básica no artificial de inicio, este modelo requiere de la realización de un número generalmente mayor de iteraciones, sin embargo, produce mejores resultados iniciales que los mismos Características Al igual que otros métodos de algoritmo de solución básica factible, se debe enviar las mayores cantidades al mayor costo posible’ este busca enviar las mayores cantidades a menor costo Tienen diferentes orígenes con diferentes destinos. Un origen puede abastecer a diferentes destinos. Al finalizar el ejercicio la oferta y la demanda deben de ser satisfecha en su totalidad y/o terminado sus valores en cero. La aproximación de Vogel finaliza en costo mínimo. Ventajas Conduce rápidamente a una mejor solución. Tiene en cuenta en el análisis la diferencia entre los menores costos de transporte Generalmente nos deja cerca al óptimo. Desventajas No aporta ningún criterio que permita determinar si la solución obtenida por este método es la mejor (óptima) o no. Requiere mayores esfuerzos de cálculos que el Método de la esquina noroeste Es más elaborado que los anteriores, más técnico y dispendioso. Aplicaciones Se utiliza para ayudar a la toma de decisiones en la realización de actividades como: control de inventarios, flujo de efectivo, programación de niveles de reservas en prensas entre otras. Este método es heurístico y suele producir una mejor solución inicial, produce una solución inicial óptima, o próxima al nivel óptimo. Objetivo Reducir al mínimo posible los costos de transporte destinados a satisfacer los requerimientos totales de demanda y materiales. Cuadro comparativo de los métodos de transporte y asignación Método Definición Características El numero de asignados es igual al número de tareas Método Húngaro Es un algoritmo de optimización el cual resuelve problemas de asignación en tiempo. Este método se usa para resolver problemas de minimización. A cada asignado se asigna exactamente una tarea Cada tarea debe realizarla exactamente un asignado construye una solución del problema primal partiendo de una solución no admisible Ventajas Desventajas Se genera una matriz de costos para la asignación de "m" personas para ser asignadas a "m" tareas Todos los costos son no-negativos El problema es un problema de minimización. el método húngaro es considerablemente más simple que el método Simplex del problema de transporte. Si la cantidad del problema es grande es difícil obtener una cantidad mínima de filas para cubrir todos los ceros de la matriz actual Aplicaciones Este modelo se aplica en modelos de asignación y minimización de costos de trabajadores a puestos, de territorios a vendedores, de contratos a postores o de trabajos a plantas Objetivo El objetivo del modelo es determinar la asignación de costo mínimo de trabajadores a puestos, de territorios a vendedores, de contratos a postores o de trabajos a plantas Determinar como deben hacerse las asignaciones para minimizar los costos totales









