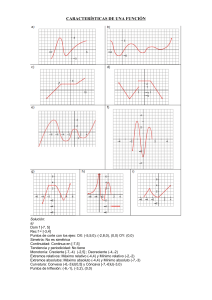
- Ninguna Categoria
Análisis Convexo: Teoría y Aplicaciones Geométricas
Anuncio
Análisis convexo
Jean Pierre Crouzeix
Eladio Ocaña
Wilfredo Sosa
December 9, 2002
PREFACIO
El análisis convexo es un tema clásico, pero fundamental para la teorı́a de
la optimización. Por lo tanto, debe ser bién entendido por los estudiantes
interesados en la teorı́a de la optimización. El objetivo de esta monografı́a
es enfocar el análisis convexo desde un punto de vista geométrico, puesto
que la geometrı́a es fundamental para la convexidad. Veremos que solo
usando la geometrı́a, podemos demostrar todos los resultados clásicos del
análisis convexo, en particular cuando se trabaja en los espacios euclidianos
de dimensión finita, ya que la topologı́a inducida por la norma euclidiana
también tiene ese ingrediente geométrico que lo hace todo más fácil.
Los temas a considerar, lógicamente no son nuevos, pero la diferencia
esta en el enfoque geométrico. En el primer y segundo capitulo consideramos los conjuntos y las funciones convexas y sus generalidades. Los
resultados considerados, lógicamente son las herramientas a utilizar en los
capı́tulos subsiguintes. En el tercer capitulo consideramos los teoremas de
separación y la conjugación de Fenchel que es fundamental para la teorı́a
de dualidad que es desarrollada en el cuarto capitulo. Finalmente en el
quinto capitulo consideramos la monotonı́a de los subdiferenciales de las
funciones convexas.
Esta monografı́a fue basada en los manuscritos del Prof. Jean Pierre
Crouzeix y fue utilizada como material para el minicurso ”Analisis Convexo” impartido por el mismo profesor del 21 de Noviembre al 16 de Diciembre del 2002 en el Instituto de Matemática y Ciencias Afines (IMCA)
de Lima (Peru).
Lima, Enero del 2003
Jean Pierre Crouzeix
Eladio Ocaña
Wilfredo Sosa
Contenido
1 Convexidad
1.1 Conjuntos convexos . . . . . . . . . . . .
1.2 Propiedades topológicas . . . . . . . . .
1.2.1 Propiedades relativas a abiertos .
1.2.2 Propiedades relativas a cerrados
1.3 Teorema de Caratheodory . . . . . . . .
1.4 Conos asintóticos . . . . . . . . . . . . .
1.5 Convexos y aplicaciones lineales . . . . .
.
.
.
.
.
.
.
1
1
5
5
6
8
10
12
2 Funciones convexas
2.1 Generalidades de las funciones de IRn en IR . . . . . . . . .
2.2 Funciones convexas de IRn en IR . . . . . . . . . . . . . . .
2.3 Funciones asintóticas . . . . . . . . . . . . . . . . . . . . . .
16
16
20
25
3 Conjugación y Subdiferencial
3.1 Teorema de separación . . . . . . . . . . . . .
3.2 Conos polares . . . . . . . . . . . . . . . . . .
3.3 Funciones conjugadas . . . . . . . . . . . . .
3.3.1 Introducción geométrica . . . . . . . .
3.3.2 Definición . . . . . . . . . . . . . . . .
3.4 Funciones indicatriz y soporte de un conjunto
3.5 Función ası́ntota y conjugación . . . . . . . .
3.6 Subdiferencial de una función convexa . . . .
31
31
35
36
36
37
41
43
45
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3.7
3.8
3.9
Derivadas direccionales de una función convexa . . . . . . .
Derivadas de una función convexa . . . . . . . . . . . . . .
Subdiferencial de la suma de dos
funciones convexas . . . . . . . . . . . . . . . . . . . . . . .
47
50
52
4 Introducción a la Dualidad Convexa
4.1 Esquema General . . . . . . . . . . . . . . . . . . . . . . . .
4.1.1 Noción del Lagrangiano . . . . . . . . . . . . . . . .
4.2 Dualidad en Programación Lineal . . . . . . . . . . . . . . .
4.3 Pertubación vertical con solo restricciones de desigualdad .
4.4 Perturbación Vertical - Caso General . . . . . . . . . . . .
4.5 Ejemplo de perturbaciones no Verticales . . . . . . . . . . .
4.6 Inf convolución y el Sub diferencial de la suma de dos funciones convexas . . . . . . . . . . . . . . . . . . . . . . . . .
4.7 Subdiferencial de una función máximo de funciones . . . .
53
53
56
58
60
62
64
5 Monótonia y continuidad del subdiferencial
5.1 Nociones generales sobre las multiaplicaciones . . . . . .
5.2 Monotonı́a del subdiferencial . . . . . . . . . . . . . . .
5.3 Continuidad de una multiaplicación . . . . . . . . . . . .
5.4 Continuidad del subgradiente . . . . . . . . . . . . . . .
5.4.1 Aplicación a la sensibilidad . . . . . . . . . . . .
5.4.2 Propiedades genéricas de las funciones convexas
5.5 -subdiferenciales . . . . . . . . . . . . . . . . . . . . . .
72
72
73
74
76
77
80
84
0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
66
70
Capı́tulo 1
Convexidad
1.1
Conjuntos convexos
Definición 1.1.1 Un conjunto C ⊂ IRn es convexo si:
∀x ∈ C, ∀y ∈ C y ∀t ∈ [0, 1] : tx + (1 − t)y ∈ C
Observación, La definición de convexidad es meramente vectorial y unidimensional, es decir que no se requiere de ninguna topologı́a ni de otras
estructuras matemáticas excepto la vectorial, para definirla y la verificación
es hecha sobre un segmento de recta.
Definición 1.1.2 Dados x ∈ IRn y C ⊂ IRn . Se dice que x es una combinación convexa de elementos de C, si existen: p ∈ IN, {ti }pi=1 ⊂ [0, 1] y
Pp
Pp
{xi }pi=1 ⊂ C tales que x = i=1 ti xi y i=1 ti = 1.
Proposición 1.1.1 Dado C ⊂ IRn . C es convexo si y solo si contiene
todas las combinaciones convexas de C.
Demostración. La Definición 1.1.1 implica que todo conjunto que contiene a todas sus combinaciones convexas es un conjunto convexo. La
recı́proca es consecuencia de la inducción matemática. En efecto, la Definición 1.1.1 implica que vale para p = 1 y para p = 2. Por hipótesis de
1
inducción, supongamos que vale para p > 2, entonces debemos probar que
p+1
vale para p + 1. Para esto considere {xi }p+1
i=1 ⊂ C y {ti }i=1 ⊂ [0, 1] tal que
Pp+1
Pp+1
x = i=1 ti xi y i=1 ti = 1. Sin perdida de generalidad supongamos que
Pp
(caso contrario ti = 0 ∀i = 1, · · · , p, ası́ x = xp+1 ∈ C). Hai=1 ti 6= 0
Pp
Pp
Pp
ciendo t = i=1 ti y y = i=1 tti xi , se tiene que i=1 tti = 1, tp+1 = 1 − t
y x = ty + (1 − t)xp+1 . Por la hipótesis de inducción y ∈ C y por la
Definición 1.1.1 x ∈ C.
Proposición 1.1.2 Si I es un conjunto de indices cualquiera y {Ci }i∈I es
una familia de conjuntos convexos de IRn , entonces ∩i∈I Ci es también un
conjunto convexo.
Demostración. Queda como ejercicio para el lector.
Definición 1.1.3 Dado un conjunto S ⊂ IRn no vacı́o, diremos que la
cápsula convexa de S, la cual denotaremos como co(S), es la intersección
de todos los conjuntos convexos que contienen a S.
Observación, la cápsula convexa co(S) de un conjunto S es también convexa, resulta de aplicar la Proposición 1.1.2. Más aún, la cápsula convexa
de un conjunto S, es el menor conjunto convexo que contiene a S.
Proposición 1.1.3 La cápsula convexa de un conjunto S ⊂ IRn no vacio,
es el conjunto de todas las combinaciones convexas del conjunto S.
Demostración. Sea D el conjunto de todas combinaciones convexas de
S, entonces S ⊂ D. Por la Proposición 1.1.1 D es convexo, por lo tanto
S ⊂ co(S) ⊂ D. Recı́procamente, sea y ∈ D, esto implica que y es una
combinación de elementos de S ⊂ co(S), ası́ y también es una combinación
convexa de elementos de co(S). Finalmente, usando la Proposición 1.1.1,
se tiene que y ∈ co(S).
Corolario 1.1.1 S1 ⊂ S2 implica que co(S1 ) ⊂ co(S2 ).
Demostración. Queda como ejercicio para el lector.
2
Definición 1.1.4 K ⊂ IRn es un cono, si ∀x ∈ K, ∀λ > 0 : λx ∈ K.
El cono K es llamado sin punta, si 0 ∈
/ K.
El cono K es llamado convexo si K es un conjunto convexo.
Proposición 1.1.4 Dado K ⊂ IRn .
a) K es un cono convexo si y solo si K es un cono y se verifica que x + y ∈
K para cada x, y ∈ K.
b) Si I es un conjunto de indices cualquiera y {Ki }i∈I es una familia de
conos en IRn , entonces ∩i∈I Ki es también un cono.
Demostración. queda como ejercicio para el lector.
Dado un conjunto S ⊂ IRn , consideremos la familia de todos los conos
que contienen a S (esta familia es no vacı́a, pues contiene a IRn ). La
intersección de los conos que contienen a S es también un cono que contiene
a S y es el cono más pequeño que contiene a S. Este cono es llamado la
cápsula cónica de S generada por S y es denotada por con(S). Si a la
cápsula cónica de S le incluimos el origen, entonces obtenemos un cono que
es llamado cono generado por S y es denotado por cono(S).
Proposición 1.1.5 Sea S ⊂ IRn .
a) con(S) := {λx : x ∈ S, λ > 0}
b) cono(S) := {λx : x ∈ S, λ ≥ 0}
c) Si S es convexo, entonces con(S) y cono(S) son también convexos.
Demostración. Queda como ejercicio para el lector.
Dado un conjunto S ⊂ IRn , ahora consideremos la familia de todos los
conos convexos que contienen a S (esta familia también es no vacı́a pues
contiene a IRn ). La intersección de los conos convexos que contienen a S,
es también un cono convexo, más aún es el cono convexo más pequeño que
3
contiene a S, el cual es llamado cápsula convexa cónica de S. Si a esta
cápsula convexa cónica de S le incluimos el origen, entonces obtenemos el
cono convexo generado por S.
Proposición 1.1.6 Sea S ⊂ IRn , S 6= ∅.
a) La cápsula convexa cónica de S y la cápsula convexa cónica de co(S)
coinciden.
b) Los conos convexos generados respectivamente por S, co(S) y co(S)∪{0}
coinciden.
Demostración. Queda como ejercicio para el lector.
Dado H ⊂ IRn , H 6= ∅. Se dice que H es un subespacio afı́n de IRn si
existe a ∈ H tal que H − a := {h − a : h ∈ H} es un subespacio vectorial de
IRn . Note que H es un conjunto convexo y que H −a = H −b ∀a, b ∈ H. La
dimensión de H (dim(H)) es la dimensión del subespacio vectorial H − a.
Proposición 1.1.7 Si I es un conjunto de indices cualquiera y {Hi }i∈I es
una familia de subespacios afines de IRn , entonces ∩i∈I Hi es un subespacio
afı́n de IRn .
Demostración. Queda como ejercicio para el lector.
Dado un conjunto S ⊂ IRn , consideremos la familia de subespacios
afines que contienen a S (esta familia también es no vacı́a pues contiene
a IRn ). La intersección de estos subespacios afines que contienen a S es
también un subespacio afı́n y es el más pequeño de los subespacios afines
que contiene a S y se llamará subespacio afı́n generado por S y es denotado
por af f (S). Por definición, la dimensión de S es la dimensión de af f (S).
Proposición 1.1.8 Sea S ⊂ IRn , S 6= ∅ y a ∈ S.
Pp
1. af f (S) = {a + i=1 ti (bi − a) : p ∈ IN, {ti }pi=1 ∈ IR, {bi }pi=1 ∈ S}.
2. S1 ⊂ S2 implica af f (S1 ) ⊂ af f (S2 ).
4
3. af f (S) = af f (co(S)).
Demostración. Queda como ejercicio para el lector.
Observación, Sea S ⊂ IRn , en general af f (S) 6= af f (con(S)).
1.2
1.2.1
Propiedades topológicas
Propiedades relativas a abiertos
Sea S ⊂ IRn no vacı́o. Se define el interior relativo de S, denotado por
ri(S), al interior de S en la topologı́a relativa de af f (S). Observe que en
general S1 ⊂ S2 no implica que ri(S1 ) ⊂ ri(S2 ). Por ejemplo considere en
IR2 , S1 = [0, 1] × {0} y S2 = [0, 1] × [0, 1].
Una propiedad topológica fundamental de los conjuntos convexos es la
siguiente.
Teorema 1.2.1 El interior relativo de un conjunto convexo no vacı́o es
no vacı́o.
Demostración. Sin perdida de generalidad supongamos que dim(S) = n
y que 0 ∈ S. Como dim(S) = n, entonces existen n vectores linealmente
independientes {x1 , · · · , xn } ⊂ S. Ahora consideremos
T := {
n
X
ti xi :
{ti }ni=1
i=1
⊂ (0, 1),
n
X
ti < 1}
i=1
entonces T ⊂ S. Por otro lado es fácil ver que T es un conjunto abierto,
pues es la imagen de un conjunto abierto por medio de una aplicación lineal
Pn
biyectiva que lleva (t1 , · · · , tn ) ∈ IRn → i=1 ti xi ∈ IRn .
Corolario 1.2.1 Si C ⊂ IRn es convexo, entonces af f (C) = af f (ri(C)).
Demostración. Sabemos que ri(C) ⊂ C, esto implica que af f (ri(C)) ⊂
af f (C). Por otra parte: C convexo implica ri(C) 6= ∅. Luego ri(C)
5
contiene una bola en la topologı́a relativa de af f (C), esto implica que
af f (C) ⊂ af f (ri(C)).
Teorema 1.2.2 Si C es convexo entonces ri(C) es convexo.
Demostración. Sin perdida de generalidad, supongamos que dim(C) =
n. Sean x, y ∈ int(C) y t ∈ [0, 1], luego existe r > 0 tal que B(x, r),
B(y, r) ⊂ C. Sea d ∈ IRn tal que ||d|| < r, entonces x + d ∈ C, y + d ∈ C,
esto implica que x + d + t(y − x) ∈ C, por lo tanto B(x + t(y − x), r) ⊂ C.
1.2.2
Propiedades relativas a cerrados
Proposición 1.2.1 Si S ⊂ IRn , entonces af f (S) = af f (S).
Demostración. Queda como ejercicio para el lector.
Observación, Es fácil ver que en IR los conjuntos convexos son los intervalos. Por otro lado, la clausura de un intervalo sigue siendo un intervalo
y por lo tanto convexo. Una generalización de esta observación es dada en
el siguiente resultado.
Proposición 1.2.2 Si C ⊂ IRn es convexo, entonces C es convexo.
Demostración. Sean a, b ∈ C, t ∈ [0, 1] y > 0, luego existen a0 ∈ C,
b0 ∈ C tales que ||a − a0 || < y ||b − b0 || < , luego
||a0 + t(b0 − a0 ) − a + t(b − a)|| ≤ (1 − t)||a0 − a|| + t||b − b0 || ≤ esto implica que a0 + t(b0 − a0 ) ∈ B(a + t(b − a), ).
Proposición 1.2.3 Sean C convexo y no vacı́o, x̄ ∈ ri(C), ȳ ∈ C y t ∈
]0, 1[ implican que x̄ + t(ȳ − x̄) ∈ ri(C).
Demostración. Sin perdida de generalidad, supongamos que dim(C) = n,
pues af f (ri(C)) = af f (C) = af f (C). Sea t ∈]0, 1[, z̄ = x̄ + t(ȳ − x̄) (se
6
supone que x̄ 6= ȳ), luego existe r > 0 tal que r < ||x̄ − z̄|| y V = {x ∈ IRn :
||x − x̄|| < r} ⊂ C, luego z̄ ∈
/ V , ȳ ∈
/ V y V ⊂ int(C). Sea
T := {y ∈ IRn : ∃x ∈ V, t ∈]0, 1[, z̄ = x + t(y − x)}
entonces
T = {y ∈ IRn : ∃x ∈ V, λ > 0, y = z̄ − λ(x − z̄)}
luego T es un cono abierto y ȳ ∈ T ∩ C, esto implica que existe ŷ ∈ T ∩ C.
Ahora considere U := {z ∈ IRn : ∃x ∈ V, µ ∈]0, 1[, z = ŷ + µ(x − ŷ)}. Es
fácil verificar que U es abierto y que U ⊂ C, luego z̄ ∈ U ⊂ C, esto implica
que z̄ ∈ int(C).
Proposición 1.2.4 Si C es no vacı́o y convexo, entonces:
1. ri(C) = ri(C).
2. ri(C) = C.
Demostración.
1. Sabemos que af f (C) = af f (C) y C ⊂ C. Tomemos z̄ ∈ ri(C),
sabemos que existe x̄ ∈ ri(C), esto implica que existe ȳC y t̄ ∈]0, 1[
tal que z̄ = x̄ + t̄(ȳ − x̄), finalmente usando la proposición anterior
tenemos que z̄ ∈ ri(C)
2. Sabemos que ri(C) ⊂ C. Sea ȳ ∈ C, como C 6= ∅, entonces existe
x̄ ∈ ri(C), luego para todo n ∈ IN zn = x̄ + (1 − n1 )(ȳ − x̄) ∈ ri(C),
esto implica que ȳ ∈ ri(C).
Sea S ⊂ IRn . Consideremos la familia de conjuntos convexos cerrados
que contienen a S, esta familia es no vacı́a porque contiene a IRn . La
intersección de todos los conjuntos convexos y cerrados que contienen a
S es el conjunto convexo cerrado más pequeño que contiene a S. Esta
intersección es llamada la cápsula convexa cerrada de S y es denotada por
co(S).
7
Proposición 1.2.5
co(S) = co(S)
Demostración. Queda como ejercicio para el lector.
Observación, Note que en general, si C es un convexo y cerrado, entonces
el cono generado por C no es necesariamente cerrado. En efecto, en IR2
considere
C := {(x, y) : x > 0, y > 0, xy ≥ 1}
Este mismo ejemplo muestra que la proyección de un convexo y cerrado,
no necesariamente es cerrado, pero la proyección de un convexo es siempre
un conjunto convexo.
Frontera de un conjunto convexo Dado S ⊂ IRn . Se define y se denota
la frontera de S como:
/ int(S)}
F r(S) := {x ∈ S : x ∈
Proposición 1.2.6 Si C es convexo, entonces las fronteras relativas de C,
de ri(C) y de C coinciden.
Demostración. Queda como ejercicio para el lector.
1.3
Teorema de Caratheodory
Teorema 1.3.1 Sea S ⊂ IRn , S 6= ∅ y sea x0 ∈ S fijo. Si x ∈ S, entonces
existen: p ∈ IN, {ti }pi=1 ⊂]0, +∞[ y {xi }pi=1 ⊂ S; tales que:
Pp
• x = x0 + i=1 ti (xi − x0 ).
Pp
•
i=1 ti ≤ 1
• Los vectores {xi − x0 }pi=1 son linealmente independientes.
8
Demostración. Como x ∈ S ⊂ co(S), entonces existe p ∈ IN, {ti }pi=0 ⊂
Pp
Pp
[0, 1] y {xi }pi=0 ⊂ S tales que i=0 ti = 1 y x = i=1 ti xi (eventualmente
t0 = 0), luego
x = x0 +
p
X
ti (xi − x0 ),
i=1
p
X
ti = 1 − t 0 ≤ 1
(1.1)
i=1
Sin perdida de generalidad, supongamos que ti > 0 ∀i = 1, · · · , p. Si los
vectores {xi − x0 }pi=1 son linealmente independientes, entonces habremos
probado el teorema, caso contrario existen {µi }pi=1 ⊂ IR no todos nulos
tales que
p
X
µi (xi − x0 ) = 0
(1.2)
i=1
Pp
podemos suponer que i=1 µi ≥ 0 (caso contrario tomamos µi = −µi ).
µ
Seleccionemos i0 ∈ {1, · · · , p} tal que tii0 = max[ µtii : i = 1, · · · , p], esto
0
implica que µi0 > 0. Sin perdida de generalidad, podemos suponer i0 = p,
entonces
µp
µi
≥
∀i = 1, · · · , p − 1
(1.3)
tp
ti
Combinando las ecuaciones (1.3) y (1.2) obtenemos:
x = x0 +
p−1
X
(ti −
i=1
considerando t0i = ti −
1, · · · , p − 1, más aún
p−1
X
i=1
µi
µp tp
t0i =
µi
tp )(xi − x0 )
µp
(1.4)
y la ecuación (1.3), se tiene que t0i ≥ 0 ∀i =
p−1
X
i=1
ti −
p−1
p−1
X
tp X
µi ) ≤
ti ≤ 1
µp i=1
i=1
repetir este proceso (desde la ecuación 1.2 hasta que los vectores resultantes
sean linealmente independientes.
Teorema 1.3.2 Teorema de Caratheodory. Sea S ⊂ IRn , para obtener su
cápsula convexa, es suficiente considerar las combinaciones convexas de a
lo mas (n + 1) elementos de S
9
Demostración. Como consecuencia directa del Teorema 1.3.1 tenemos
Pp
P
que: si x ∈ co(S), entonces x = i=0 ti xi con t0 = 1 − ti . Los vectores
(xi − x0 ) son linealmente independiente, en consecuencia se tiene que p ≤
n.
Teorema 1.3.3 La cápsula convexa de un conjunto cerrado y acotado es
cerrado y acotado
Demostración. Sea S cerrado y acotado (entonces compacto). Si x ∈
n+1
co(S) entonces existen {xi }n+1
i=1 ⊂ S, {ti }i=1 ⊂ [0, 1] (hacer eventualmente
Pn+1
Pn+1
ti = 0) tales que i=1 ti = 1 y x = i=1 ti xi . Consideremos
T = {t ∈ IRn+1 : {ti }n+1
i=1 ⊂ [0, 1],
n+1
X
ti = 1}
i=1
el cual es un conjunto compacto y sea f : IRn ×(IRn )n+1 → IRn definida por
P
f (t, x1 , x2 , ..., xn+1 ) =
ti xi , f es continua. Observe que co(S) = f (T ×
n+1
S
), luego co(C) es compacto como imagen de un conjunto compacto
por una aplicación continua.
1.4
Conos asintóticos
Sea C ⊂ IRn convexo no vacı́o y a ∈ C. Ahora considere
C∞ (a) = {d ∈ IRn : a + λd ∈ C, ∀λ > 0}
Se observa inmediatamente que 0 ∈ C∞ (a) y que C∞ (a) es un cono, más
aún, este cono es convexo. En efecto: sean d1 , d2 ∈ C∞ (a) hay que probar
que d1 + d2 ∈ C∞ (a), es decir a + λ(d1 + d2 ) ∈ C para todo λ > 0. Pero
a + λ(d1 + d2 ) = 12 (a + 2λd1 ) + 12 (a + 2λd2 ) ∈ C.
Observación, En general C∞ (a) depende de a, por ejemplo considere:
[
C = {(x, y) : x > 0, y > 0} {(0, 0)}
10
Es fácil ver que C es convexo. Además
[
C∞ ((0, 0)) = {(0, 0)} C
C∞ ((1, 1)) = {(x, y) : x ≥ 0, y ≥ 0}.
Definición 1.4.1 Dado C ⊂ IRn convexo no vacı́o, se llama cono de reT
cesión de C (o cono asintótico de C) al conjunto C∞ = a∈C C∞ (denotado
por Rockafellar O+ C). Los elementos d ∈ C∞ son llamadas direcciones de
recesión de C.
Teorema 1.4.1 Sea C ⊂ IRn convexo cerrado no vacı́o, entonces
C∞ (a) = C∞ (b) ∀ a, b ∈ C
además C∞ := C∞ (a) = C∞ (b) es cerrado
Demostración.
a) Mostraremos que C∞ (a) ⊂ C∞ (b). Sea d ∈ C∞ (a), λ > 0 se va
mostrar que b + λd ∈ C. Se sabe que a + nλd ∈ C ∀n ∈ IN, luego
(1 − n1 )b + n1 (a + nλd) ∈ C (por la convexidad de C y porque b ∈ C),
en consecuencia (1 − n1 )b + n1 a + λd ∈ C, haciendo tender n → ∞ y
utilizando el hecho de que C es cerrado se tiene que b + λd ∈ C.
b) Por simetrı́a C∞ (b) ⊂ C∞ (a)
c) Sea {dn }i∈IN ⊂ C∞ tal que dn → d mostraremos que d ∈ C∞ , es
decir a + λd ∈ C ∀λ > 0. Se sabe que a + λdn ∈ C ∀n, dn → d y
C cerrado, en consecuencia a + λd ∈ C.
Proposición 1.4.1 Sea C ⊂ IRn convexo cerrado y no vacı́o. Entonces C
es acotado si y solo si C∞ = {0}
Demostración.
a) Si C es acotado entonces trivialmente C∞ = {0}
b) Supongamos que C no es acotado, entonces mostraremos que C∞ no
se reduce al origen. Fijemos a ∈ C, entonces ∀n ∈ IN ∃{xn }n∈IN ∈ C
11
−a
tal que kxn −ak ≥ n. Consideremos dn = kxxnn −ak
, entonces kdn k = 1,
n
luego ∃d ∈ IR , kdk = 1 y una sub sucesión dnk → d. Se va mostrar
que d ∈ C∞ . Sea λ > 0 cualquiera, como a ∈ C y xnk ∈ C, entonces
tkx −ak
a+t(xnk −a) ∈ C ∀ t ∈]0, 1[, luego a+ nλk
(λdnk ) ∈ C ∀ t ∈]0, 1[.
Considerando tnk = kxn λ−ak se tiene que a + λdnk ∈ C ∀k ≥ k0 . Si
k
k → ∞ entonces dnk → d, C cerrado y en consecuencia a + λd ∈ C.
Sea C convexo cerrado no vacı́o,luego es fácil verificar que el conjunto
T
C∞ (−C∞ ) es un subespacio vectorial de IRn , el cual se llamará espacio de
T
linealidad de C (“lineality space”). Ahora considerando L = C∞ (−C∞ )
se tiene que
\
C = L + (C
L⊥ )
donde L⊥ = {y : hx, yi = 0 ∀x ∈ L}
Proposición 1.4.2 Si Ci son convexos cerrados de IRn y C =
T
entonces C∞ = i (Ci )∞
T
Ci 6= ∅,
Demostración. Queda como ejercicio para el lector.
1.5
Convexos y aplicaciones lineales
Imagen Recı́proca Sea A : IRn → IRp una aplicación lineal y C ⊂ IRp ,
se considera A− (C) = {x ∈ IRn : Ax ∈ C}. Debido a que A es continua,
A− (C) es abierto cuando C es abierto, cerrado cuando C es cerrado. Se
demuestra también fácilmente que A− (C) es convexo si C es convexo.
Imagen Sea A : IRn → IRp una aplicación lineal y C ⊂ IRn se considera
A(C) = {y ∈ IRp : ∃ x ∈ C con y = Ax}. Se verifica fácilmente que
A(C) ⊂ A(C) y que si C es convexo, entonces A(C) es convexo.
Proposición 1.5.1 Si C ⊂ IRn es convexo no vacı́o y A : IRn → IRp es
una aplicación lineal, entonces
A(ri(C)) = ri(A(C)) = ri(A(C))
12
Demostración. Es fácil verificar que:
A(ri(C)) ⊂ A(C) ⊂ A(C) = A(ri(C)) ⊂ A(ri(C)) ⊂ A(C)
esto implica que A(ri(C)) = A(C) = A(C) y como ri(D) = ri(D) entonces
se tiene
ri(A(C)) = ri(A(C)) = ri(A(ri(C))) ⊂ A(ri(C))
Para la recı́proca, tome ȳ ∈ A(ri(C)) y yb ∈ ri(A(C)) (b
y existe debido a que
A(C) 6= ∅). Luego, existen x̄ ∈ ri(C) y x
b ∈ C tal que ȳ = Ax̄ y yb = Ab
x.
Como x̄ ∈ ri(C), existe x̃ ∈ ri(C) y t ∈]0, 1[ tal que x̄ = tx̂ + (1 − t)x̃ y por
lo tanto ȳ = tŷ + (1 − t)ỹ, siendo ỹ = A(x̃). Debido a que ŷ ∈ ri(A(C)) y
ỹ ∈ A(C), entonces se tiene que ȳ ∈ ri(A(C)).
Sea C ⊂ IRn un conjunto cerrado no vacı́o y sea A : IRn → IRp una
aplicación lineal. A(C) es cerrado?. Este es verdad si además el conjunto
C es acotado; porque la imagen de un compacto por una aplicación continua
es compacto y en consecuencia cerrado. Este es falso en general, por ejemplo
considere:
C = {(x, y) ∈ IR2 : x > 0, y > 0, xy ≥ 1}
A : IR2 → IR tal que A(x, y) = x
Entonces A(C) =]0, +∞[ no es cerrado. (Aquı́ A(C) es la proyección de C
sobre el eje x)
Teorema 1.5.1 sea A : IRn → IRp una aplicación lineal. C ⊂ IRn convexo
no vacı́o. Si la siguiente condición es satisfecha:
Para d ∈ IRn : Ad = 0 y d ∈ (C)∞ ⇒ −d ∈ (C)∞ ,
entonces,
a) A(C) = A(C)
b) A(C ∞ ) = [A(C)]∞
Demostración.
13
a) Se tiene siempre A(C) ⊂ A(C) ⊂ A(C) ⊂ A(C). Poniendo D = C es
suficiente demostrar que A(D) es cerrado. Sin perdida de generalidad
T
T
se supone que 0 ∈ D. Sea L = D∞ (−D∞ ) {d : Ad = 0} y L⊥
e = D T L⊥ entonces D
e es
el sub espacio ortogonal de L. Tomando D
e + L, A(D) = A(D).
e Por otro lado
cerrado, D = D
\
\
\
e ∞ {d : Ad = 0} = (L⊥ )∞ D∞ {d : Ad = 0} =
D
L⊥
\
D∞
\
(−D∞ )
\
{d : Ad = 0} = {0}
e existe una sucesión
e es cerrado. Sea ȳ ∈ A(D),
Mostraremos que A(D)
e
e T{x : kAx− ȳk ≤
{xn } tal que xn ∈ D y Axn → ȳ. Considere K = D
1}, K es convexo cerrado. Se verifica que {x : kAx − ȳk ≤ 1}∞ =
e ∞ T d : Ad = 0 = {0} y
{d : Ad = 0}. Se sigue que K∞ = (D)
K es acotado. Por consiguiente la sucesión {xn } es acotada, sea x̄
e Ax̄ = ȳ y
un elemento de la adherencia, se tiene entonces x̄ ∈ D,
e
ȳ ∈ A(D).
b) Se va mostrar que A(D∞ ) = [A(D)]∞ . Sea d ∈ D∞ , debido a que
0 ∈ D se tiene λd ∈ D ∀ λ > 0, por consiguiente λA(d) = A(λd) ∈
A(D) ∀ λ > 0 y en consecuencia Ad ∈ [A(D)]∞ . Sea v ∈ [A(D)]∞ =
e ∞ , v 6= 0. Debido a que 0 ∈ D,
e 0 ∈ A(D)
e y en consecuencia
[A(D)]
e ∀λ > 0, en particular si λ = 1 y poniendo K = {d ∈ D
e :
λv ∈ A(D)
T
e
Ad = v} = D {d : Ad = v} entonces K es convexo cerrado no vacı́o
e ∞ T{d : Ad = v} = {0} y por consiguiente K es acotado.
y K∞ = D
e existe dn ∈ K tal que ndn ∈ D.
e La sucesión
Debido a que nv ∈ A(D),
{dn } es acotada, entonces admite valor de adherencia, sea d un tal
e ∞ , acabo; en caso contrario existe
valor, entonces d ∈ K. Si d ∈ (D)
e
λ > 0 tal que λd ∈
/ D. Notemos que debido a que 0 y ndn están en
e se tiene λdn ∈ D
e ∀n > λ. Debido a que λd es valor de adherencia
D
e debido a que D
e es cerrado lo cual es una
de {λdn } entonces λd ∈ D
contradicción.
Proposición 1.5.2 Si C y D son dos conjuntos convexos de IRn , entonces
C + D es un conjunto de IRn y se tiene ri(C) + ri(D) = ri(C + D)
14
Demostración. Considere A : IRn × IRn → IRn definida por A(x, y) =
x + y entonces A(C × D) = C + D. Es fácil ver que C × D es convexo y
ri(C × D) = ri(C) × ri(D).
De manera general, la suma de dos convexos cerrados no es necesariamente
cerrado. Considere por ejemplo
C = {(x, y) ∈ IR2 : x > 0, y > 0, xy ≥ 1
C = {(x, y) ∈ IR2 : y = 0, x ≤ 0
entonces
C + D = {(x, y) : y > 0}
Teorema 1.5.2 Si C y D son dos conjuntos convexos de IRn tales que
\
\
d ∈ (C)∞ (−C)∞ ⇒ −d ∈ (C)∞ (−C)∞
entonces
C +D =C +D
y
(C + D)∞ = (C)∞ + (D)∞
Demostración. Considere la aplicación lineal A(x, y) = x + y.
15
Capı́tulo 2
Funciones convexas
2.1
Generalidades de las funciones de IRn en
IR
Dada una función f : S → IR con S ⊂ IRn , se puede siempre prolongar a
una función g : IRn → IR definida por:
(
f (x) si x ∈ S
g(x) =
+∞
si x ∈
/S
Supondremos que las funciones están definidas en IRn con valores en IR
Dada f : IRn → IR y λ ∈ IR, consideraremos:
dom(f ) = {x ∈ IRn : f (x) < +∞}
epi(f ) = {(x, λ) ∈ IRn × IR : f (x) ≤ λ}
f ) = {(x, λ) ∈ IRn × IR : f (x) < λ}
epi(f
Sλ (f ) = {x ∈ IRn : f (x) ≤ λ}
Seλ (f ) = {x ∈ IRn : f (x) < λ}
No es difı́cil verificar:
• dom(f ) =
S
λ∈IR
Sλ (f ) =
S
λ∈IR
Seλ (f )
16
dominio de f
epigrafo de f
epigrafo estricto de f
subnivel λ de f
subnivel λ estricto de f
f ))
• dom(f ) = projIRn (epi(f )) = projIRn (epi(f
• λ < µ ⇒ Seλ (f ) ⊂ Sλ (f ) ⊂ Seµ (f ) ⊂ Sµ (f )
• λ < µ y (x, λ) ∈ epi(f ) ⇒ (x, µ) ∈ epi(f )
• f (x) = inf[λ : (x, λ) ∈ epi(f )] = inf[λ : x ∈ Sλ (f )]
f )] = inf[λ : x ∈ Seλ (f )]
• f (x) = inf[λ : (x, λ) ∈ epi(f
• f1 ≤ f2 ⇔ epi(f1 ) ⊃ epi(f2 ) ⇔ Sλ (f1 ) ⊃ Sλ (f2 ) ∀ λ ∈ IR
f 1 ) ⊃ epi(f
f 2 ) ⇔ Seλ (f1 ) ⊃ Seλ (f2 ) ∀ λ ∈ IR
• f1 ≤ f2 ⇔ epi(f
T
• Sλ (f ) × {λ} = epi(f ) [IRn × {λ}] ∀ λ ∈ IR
T
f ) [IRn × {λ}] ∀ λ ∈ IR
• Seλ (f ) × {λ} = epi(f
Recordemos que:
• Una función f es llamada semicontinua inferiormente (sci) en x0 si
∀ λ < f (x0 ) existe una vecindad V de x0 tal que x ∈ V ⇒ f (x) > λ.
• Una función f es llamada semicontinua superiormente (scs) en x0 si
−f es sci en x0 , es decir ∀ λ > f (x0 ) existe una vecindad V de x0 tal
que x ∈ V ⇒ f (x) < λ.
• Una función f es llamada sci (scs) si este es sci (scs) en todo x ∈ IRn
Teorema 2.1.1 f es sci ⇐⇒ epi(f ) cerrado ⇐⇒ Sλ (f ) cerrado ∀ λ ∈
IR.
Demostración.
a) f sci ⇒ epi(f ) es cerrado. En efecto, se va mostrar que [epi(f )]c es
abierto. Sea (x0 , λ0 ) ∈
/ epi(f ), entonces λ0 < f (x0 ). Sea µ tal que
λ0 < µ < f (x0 ) entonces debido a que f es sci en x0 , existe una
vecindad V de x0 tal que x ∈ V ⇒ f (x) > µ, lo cual implica que
V ×] − ∞, µ] es una vecindad de (x0 , λ0 ) que no intersecta al epi(f ).
17
b) epi(f ) cerrado ⇒ Sλ (f ) cerrado. En efecto, esto se deduce de la
T
siguiente igualdad: Sλ (f ) × {λ} = epi(f ) [IRn × {λ}].
c) Sλ (f ) es cerrado ∀ λ ∈ IR, entonces ⇒ f es sci. En efecto, Si f (x0 ) =
−∞ entonces f es sci en x0 por definición. Si f (x0 ) > −∞ entonces
∀ < f (x0 ) se tiene que x0 ∈
/ Sλ (f ). Sλ (f ) cerrada entonces existe
una vecindad V de x0 tal que x ∈
/ Sλ (f ) ∀x ∈ V , es decir f (x) > λ
∀x∈V.
Los siguientes resultados son clásicos y bien conocidos:
• Si f y g son sci en x0 entonces f + g, min(f, g), kf , para todo k > 0
son sci en x0 .
• Sea I un conjunto de indices arbitrario. Si {fi }i∈I es una familia de
funciones sci en x0 , entonces supi∈I fi es sci en x0 .
Proposición 2.1.1 Si C es un compacto en IRn y f es sci en todo x ∈ C,
entonces existe x̄ ∈ C tal que f (x̄) = inf[f (x) : x ∈ C]
Demostración. Para todo λ > inf [f (x) : x ∈ C] = α considere Kλ =
T
{x ∈ C : f (x) ≤ λ} = C Sλ (f ). Los Kλ son compactos encajados no
T
vacı́os para todo λ > α (µ > λ ⇒ Kµ ⊃ Kλ ). Se sigue que K = λ>α Kλ
es no vacı́o. Tome x̄ ∈ K.
Proposición 2.1.2 Sean X × T ⊂ IRn , ϕ : X × T → IR y x̄ ∈ X tales
que ϕ es sci en (x̄, t) ∀ t ∈ T y T compacto. Si definimos h mediante
h(x) = inf t∈T ϕ(x, t), entonces h es sci en x̄.
Demostración. Sea λ ∈ IR tal que λ < h(x̄), entonces λ < ϕ(x̄, t)
∀t ∈ T , debido a que ϕ es sci en (x̄, t), existe una vecindad Vt × Wt de
(x̄, t) tal que (x0 , t0 ) ∈ Vt × Wt ⇒ λ < ϕ(x, t0 ). Pero T es compacto y
S
S
T , en consecuencia existen t1 , ..., tq tal que i=1,...,q Wti ⊃ T .
t∈T Wt ⊃
T
Sea V = i=1,...,q Vti , entonces V es una vecindad de x̄. Debido a que
S
Vti ⊃ V y Wti ⊃ T se tiene ϕ(x, t) > λ ∀ x ∈ V, ∀ t ∈ T y en
consecuencia h(x) ≥ λ. Se deduce que h es sci en x̄.
18
Dado una función f : IRn → IR, consideremos
= = {g : IRn → IR : g es sciy g(x) ≤ f (x)∀ x ∈ IRn }
Note que = es no vacı́o (pues contiene a la función idénticamente −∞).
Ahora consideremos supg∈= g, esta es una función sci mayorada por f y es
la mas grande función sci que es mayorada por f . Se llama regularización
sci de f y se le denota por f (cl(f )).
Proposición 2.1.3 epi(f¯) = epi(f ), Sλ (f¯) =
T
µ>λ
Sµ(f )
Demostración. Se tiene f ≤ f y en consecuencia epi(f ) ⊃ epi(f ). Debido a que f es sci epi(f ) es cerrado y en consecuencia epi(f ) ⊃ epi(f ).
Recı́procamente. Definamos g(x) = inf [λ : (x, λ) ∈ epi(f )]. Se ve que
epi(f ) = epi(g) y en consecuencia g es sci y g ≤ f , por lo tanto g ≤ f y
epi(g) = epi(f ) ⊂ epi(f ).
Proposición 2.1.4 f es sci en x0 si y solo si f (x0 ) = f (x0 ).
Demostración. Sabemos que f ≤ f . Si f (x0 ) < f (x0 ) elegimos λ ∈
]f (x0 ), f (x0 )[. Como ((x0 ), f (x0 )) ∈ epi(f¯) = epi(f ), entonces para cada
T
vecindad V de x0 V ×] − ∞, λ[ epi(f ) 6= ∅ y en consecuencia para cada
vecindad V de x0 , ∃x ∈ V tal que f (x) < λ lo cual implica que f no es sci
en x0 . Para la recı́proca, si f (x0 ) = f (x0 ). Sea λ < f (x0 ), debido a que f
es sci, existe una vecindad V de x0 tal que λ < f (x) ≤ f (x) ∀x ∈ V por
consiguiente f es sci en x0 .
T
Observación, Se tiene siempre que Sλ (f ) = µ>λ Sµ (f ) pero no necesariamente Sλ (f ) = Sλ (f ). Por ejemplo considere
(
x2 si x 6= 0
f (x) =
1
si x = 0
S0 (f ) = ∅
S0 (f ) = {0}
19
2.2
Funciones convexas de IRn en IR
a) Generalidades y primeras propiedades.
haremos la convención siguiente:
En todo lo que sigue
∞ + α = α + ∞ = +∞ ∀ α ∈ IR
−∞ + α = α − ∞ = −∞ ∀ α ∈ IR
(−∞) + ∞ = ∞ + (−∞) = +∞
Definición 2.2.1 Una función f : IRn → IR es llamado convexa si su
epı́grafo es convexa.
Por ejemplo
+∞
f (x) =
13
−∞
si x < 0
si x = 0
si x > 0
es una función convexa.
Los siguientes resultados pueden ser verificados fácilmente:
f ) es convexo
• f es convexa si y solo si epi(f
• f es convexa si y solo si ∀x, y ∈ IRn , ∀ t ∈]0, 1[ se tiene
f (tx + (1 − t)y) ≤ tf (x) + (1 − t)f (y)
• f es convexa si y solo si ∀x ∈ IRn , ∀d ∈ IRn la función de una variable
real fx,d (t) = f (x + tx) es convexa.
• Si f es convexa, entonces dom(f ) = projIRn (epi(f )) es convexa, Sλ (f )
T
es convexa ∀λ ∈ IR (Sλ (f ) × {λ} = epi(f ) IRn × {λ})
• Si f es convexa, entonces f es convexa epi(f ) = epi(f ).
• Si f es convexa y si λ > 0 entonces λf es convexa.
• Si f es convexa y k : IR → IR es una función convexa creciente
entonces kof es convexa (Utilice la definición analı́tica).
20
• Si f y g son convexas, entonces f + g es convexa.
• Sea {fi }i∈I fi : IRn → IR convexas ∀ i ∈ I entonces f = supi∈I fi es
T
convexa (epi(f ) = i∈I epi(fi ))
Proposición 2.2.1 Sea ϕ : IRn × IRp → IR y h : IRn → IRp definida por
h(x) = inf y∈IRp ϕ(x, y). Si ϕ es convexa sobre IRn × IRp entonces h es
convexa sobre IRn
Demostración.
f
epi(h)
= {(x, λ) : h(x) < λ} = {(x, λ) : ∃ y ∈ IRp con ϕ(x, y) < λ}
f
f
epi(h)
= projIRn ×IR epi(ϕ)
f
en consecuencia epi(h)
es convexa como proyección de un convexo.
b) Propiedades de las funciones convexas de una variable real.
Proposición 2.2.2 Si θ es convexa y si ∃ x0 tal que θ(x0 ) = −∞, entonces
θ no puede tomar valores finitos en puntos que no están en la frontera de
su dominio.
Demostración. dom(θ) es un intervalo I. Si θ en finito en a ∈ int(I),
tomando b ∈ int(I) y t ∈]0, 1[ tal que a = tx0 + (1 − t)b entonces θ(a) ≤
tθ(x0 ) + (1 − t)θ(b) = −∞ debido a que θ(b) < +∞.
Proposición 2.2.3 Si θ es convexa y si θ(t) > −∞ ∀t ∈ IR, entonces θ es
continua sobre int(dom(θ). Por otro lado θ admite derivada por la derecha
y por la izquierda en todo t ∈ int(dom(θ)) y se tiene
0
0
0
0
θ−
(t) ≤ θ+
(t) ≤ θ−
(s) ≤ θ+
(s)
∀ ∀ s, t ∈ int(dom(θ)) tal que s ≤ t
Demostración. Sea a, b, c ∈ int(dom(θ)) tal que a < b < c, sea t tal que
b = (1 − t)a + tc se tiene entonces θ(b) ≤ (1 − t)θ(a) + tθ(c) en la que se
tiene
θ(b) − θ(a)
θ(c) − θ(a)
θ(c) − θ(b)
≤
≤
b−a
c−a
c−b
21
θ(c)−θ(b)
∀c
c−b
θ(c)−θ(b)
0
≤ θ+ (b); ∀a
c−b
0
Fijando b y c y haciendo tender a hacia b se tiene θ−
(b) ≤
>b
Fijando a y b y haciendo tender c hacia a se tiene
Por lo que se obtiene:
<b
0
θ+
(a) ≤
θ(b) − θ(a)
θ(c) − θ(b)
0
0
0
≤ θ−
(b) ≤ θ+
(b)
≤ θ−
(c)
b−a
c−b
Teorema 2.2.1 Sea θ : I → IR diferenciable donde I es un intervalo de
IR. Una condición necesaria y suficiente para que θ sea convexa sobre I es
que θ0 sea creciente sobre I.
Demostración. El resultado precedente muestra que la condición es necesaria. Supongamos ahora que θ0 es creciente y sea a, b ∈ I, t̄ ∈]0, 1[, a < b
y c = t̄a + (1 − t)b. Existe por el teorema de valor medio x1 y x2 tales que
a < x1 < c < x2 < b con
θ0 (x1 ) ≤
θ(c) − θ(a)
θ(b) − θ(c)
, θ0 (x2 ) ≤
c−a
b−c
Pero θ0 (x1 ) ≤ θ0 (x2 ), de donde se deduce que θ(c) ≤ t̄θ(a) + (1 − t)θ(b).
Teorema 2.2.2 Sea θ : I → IR diferenciable donde I es un intervalo de
IR. θ es convexa sobre I si y solo si θ00 ≥ 0 ∀ x ∈ I
Demostración. Queda como ejercicio para el lector.
b) Primeras propiedades de las funciones de varias variables. Sea
f : IRn → IR una función.
Proposición 2.2.4 Si f es convexa y si ∃ x0 tal que f (x0 ) = −∞, entonces f (x) = −∞ ∀x ∈ ri(dom(f )). Se sigue que f no puede tomar
valores finitos en puntos que están fuera de su frontera relativa de su dominio.
22
Demostración. Sea x ∈ ri(dom(f )), entonces t ∈]0, 1[ y y ∈ dom(f )
tal que x = tx0 + (1 − t)y. Debido a que f (x0 ) = −∞, f (y) < +∞ y
f (x) ≤ tf (x0 ) + (1 − t)f (y) se tiene f (x) = −∞.
Se dirá que una función convexa es propia si f (x) > −∞ ∀ x y si exists
x ∈ IRn tal que f (x) < +∞.
Proposición 2.2.5 Si f es una función convexa y propia entonces f es
sci sobre ri(dom(f )) y f es continua sobre int(dom(f )). En particular
f (x) = f (x) ∀ x ∈ ri(dom(f ))
Demostración.
a) Si f no es sci en x0 , entonces f (x0 ) < f (x0 ) y por lo tanto se tiene
T
que x0 ∈ Sf (x0 ) (f ) = λ>f (x0 ) Sλ (f ). Considere Sλ (f ) con λ ∈
]f (x0 ), f (x0 )[. Sea x̄ ∈ ri(Sλ (f )) (este elemento existe debido a que
ri(Sλ (f )) 6= ∅), Consideremos θ(t) = f (x0 + t(x̄ − x0 )). Debido a que
f es convexa, se tiene que 0 ∈ int(dom(θ)) ( ya que x0 ∈ ri(dom(f ))
y x̄ ∈ dom(f )) y por consiguiente θ es continua en 0. Por otro lado
x0 +t(x̄−x0 ) ∈ Sλ (f ) ∀t ∈ ]0, 1[ y por consiguiente f (x0 +t(x̄−x0 )) ≤
λ. Se sigue que x0 ∈ Sλ (f ) y f (x0 ) ≤ λ, en contradicción con λ ∈
]f (x0 ), f (x0 )[. Se tiene entonces que f (x) = f (x) ∀x ∈ ri(dom(f )).
b) Es suficiente mostrar que f es scs en todo x0 ∈ int(dom(f )). Sea
λ > f (x0 ), para i = 1, · · · , n considere θi (t) = f (x0 + tei ) donde
(e1 , · · · , en ) es la base canónica de IRn . Para i = 1, · · · , n, θi es
convexa y 0 ∈ int(dom(θi )) en consecuencia θi ) es continua en 0.
Debido a que θi (0) = f (x0 ) < λ, existe ti > 0 tal que θi < λ ∀ t ∈
[−ti , ti ]. Sea S = co(x0 ± ti ei ). Debido a que x0 ± ti ei ∈ Sλ (f ) y
Sλ (f ) es convexa se tiene S ⊂ Sλ (f ). Por otro lado S es una vecindad
de x0 .
Proposición 2.2.6 Si f es convexa propia, entonces f es convexa propia.
Demostración. Se ve fácilmente que dom(f ) ⊂ dom(f ) ⊂ dom(f ) y en
consecuencia ri(dom(f )) = ri(dom(f )). Si f (x0 ) = −∞ entonces f (x) =
f (x) = −∞ ∀ x ∈ ri(dom(f )) y en consecuencia f no es propia.
23
Proposición 2.2.7 Sea C un convexo abierto de IRn y f : C → IR diferenciable. f es convexa si y solo si h∇f (y) − ∇f (x), y − xi ≥ 0 ∀ x, y ∈ C
Demostración. Sea x ∈ C y d ∈ IRn . Considere θ(t) = f (x + td)
• Si f es convexa, θ es convexa. Tomando d = y − x entonces debido a
que θ0 (0) ≤ θ0 (1) se tiene h∇f (x), y − xi ≤ h∇f (y), y − xi.
• Si h∇f (y) − ∇f (x), y − xi ≥ 0 ∀ y ∈ C se deduce que θ0 es creciente
y en consecuencia θ es convexa.
Proposición 2.2.8 Sea C un convexo abierto de IRn y f : C → IR dos
veces diferenciable. f es convexa sobre C si y solo si ∇2 f (x) es semidefinida
positiva sobre C
Demostración. Como antes, considere θ(t) = f (x + td). Se ve que
f es convexa si y solo si θ00 (0) ≥ 0 ∀ x, d en consecuencia si y solo si
h∇2 f (x)d, di ≥ 0 ∀ x, d
Observación, Una función convexa propia sci no es necesariamente continua sobre la frontera de su dominio, para ello considere el siguiente ejemplo:
(
x2
si y > 0
y
f (x, y) =
+∞ en otros casos
!
2
y2
−xy
2
∇ f (x, y) = 3
y
−xy x2
Por consiguiente f es convexa sobre IR×]0, +∞[.
(
{(x, y) : y > 0, x2 − λy ≤ 0}
Sλ (f ) =
∅
Pero f (x, y) = inf [λ : (x, y) ∈ Sλ (f )]
x2
y
f (x, y) =
0
+∞
si λ ≥ 0
si λ < 0
y en consecuencia
24
si y > 0
si x = y = 0
en otros casos
Notemos que f ( n1 , n12 ) = 1 ∀n ∈ IN en consecuencia f no es s.c.s en (0, 0)
Proposición 2.2.9 Sea f convexa propia, entonces
dim(Sλ (f )) = dim(dom(f )) ∀ λ > inf f (x)
x
Demostración. Como f es propia, entonces existe x0 ∈ dom(f ) tal que
f (x0 ) < λ. Sea x1 ∈ ri(dom(f )), entonces f [(x0 + t(x1 − x0 )) = f (xt ) ≤
f (x0 ) + t[f (x1 ) − f (x0 )]. ∃t̄ ∈]0, 1[ tal que f (xt̄ ) < λ. Ası́ xt̄ ∈ ri(dom(f )).
La restricción de f al af f (dom(f )) es continua en xt̄ y en consecuencia
Sλ (f ) contiene una vecindad de xt̄ para la topologı́a de af f (dom(f )).
2.3
Funciones asintóticas
Sea f una función convexa sci propia, entonces epi(f ) es un convexo cerrado. Considere (epi(f ))∞ . Se observa que (0, 1) ∈ (epi(f ))∞ que es un
cono convexo cerrado, en consecuencia
(d, λ) ∈ (epi(f ))∞ y µ > λ ⇒ (d, µ) ∈ (epi(f ))∞
Luego (epi(f ))∞ es el epı́grafo de una función convexa sci que se denotara
por f∞ (o f 0+ Rockafellar), se llamara la función asintótica de f o función
de recesión de f
Proposición 2.3.1 Sea f una función convexa sci propia, entonces f es
positivamente homogénea de grado 1, es decir:
f∞ (kd) = kf∞ (d) ∀ k > 0, f∞ (0) = 0
Demostración.
a) (d, f∞ (d)) ∈ (epi(f ))∞ que es un cono, por lo tanto (kd, kf∞ (d)) ∈
(epi(f ))∞ y ası́ f∞ (kd) ≤ kf∞ (d) ∀ k > 0.
De la misma manera (kd, f∞ (kd)) ∈ (epi(f ))∞ ⇒ (d, k1 f∞ (kd)) ∈
(epi(f ))∞ y en consecuencia f∞ (d) ≤ k1 f∞ (kd) ∀ k > 0.
25
b) Se sabe que (0, 0) ∈ (epi(f ))∞ y en consecuencia f∞ (0) ≤ 0. Por
otro lado debido a que f es propia, existe a tal que f (a) < +∞.
(a, f (a)) ∈ epi(f ) y (0, f∞ (0)) ∈ (epi(f ))∞ ⇒ (a + λ0, f (a) +
λf∞ (0)) ∈ epi(f ) ∀ λ > 0. f (a) ≤ f (a) + λf∞ (0) ∀ > 0 ⇒ f∞ (0) ≥
0.
Proposición 2.3.2 Sea f convexa sci propia y a ∈ dom(f ), entonces
f∞ (d)
(a)
= supk>0 f (a+kd)−f
k
(a)
= limk→+∞ f (a+kd)−f
k
= limk→+∞ f (a+kd)
k
Demostración. Sean (a, f (a)) ∈ epi(f ) y (d, f∞ (d)) ∈ (epi(f ))∞ , entonces (a + kd, f (a) + kf∞ (d)) ∈ (epi(f ))∞ ∀k > 0, por lo tanto se tiene
(a)
(a)
que f (a+kd)−f
≤ f∞ (d) ∀k > 0. Sea ahora m ≥ supk>0 f (a+kd)−f
,
k
k
entonces f (a + kd) ≤ f (a) + km ⇒ (a + kd, f (a) + kf∞ (d)) ∈ (epi(f ))∞
∀k > 0 y en consecuencia (d, m) ∈ (epi(f ))∞ ⇒ f∞ (d) ≤ m. Considere ahora la función θ(t) = f (a + td) − f (a), esta función es convexa
0
y se tiene por dicha propiedad que θ(t)−θ(0)
≤ θ(tt)−θ(0)
∀ t0 > t y por
0 −0
t−0
lo tanto la función k →
(a)
limk→+∞ f (a+kd)−f
.
k
f (a+kd)−f (a)
k
es creciente y supk>0
f (a+kd)−f (a)
k
=
Ejemplos.
(
x
f (x) = e , entonces f∞ (d) =
0
+∞
si d ≤ 0
si d > 0
f (x) = 12 hx, Axi − hb, xi con A simétrica semi definida positiva
(
−hb, di si Ad = 0
f∞ (d) =
+∞
en caso contrario
(
0
si d = 0
f (x) = kxk, entonces f∞ (d) =
+∞ en caso contrario
Teorema 2.3.1 Sea f una función convexa propia y sci, entonces f∞ es
propia y S0 (f∞ ) = [Sλ (f )]∞ ∀λ tal que Sλ (f ) 6= ∅
26
Demostración.
a) Sea a ∈ dom(f ), se tiene por la proposición anterior que f∞ (d) ≥
f (a + d) − f (a) en consecuencia f∞ (d) > −∞. Por otro lado f∞ (0) =
0. Se sigue que f∞ es propia.
b) Sea d ∈ S0 (f∞ ), es decir (d, 0) ∈ (epi(f ))∞ y sea a ∈ Sλ (f ), es decir
(a, λ) ∈ epi(f ) entonces se tiene (a + kd, λ) ∈ epi(f ) en consecuencia
a + kd ∈ Sλ (f ) ∀ k > 0 , de esta manera d ∈ [Sλ (f )]∞ .
Recı́procamente sea d ∈ [Sλ (f )]∞ y sea a ∈ Sλ (f ), se tiene a +
kd ∈ Sλ (f ), es decir (a + kd, λ) ∈ epi(f ) ∀ k > 0 y por lo tanto
(d, 0) ∈ [epi(f )]∞ es decir f∞ (d) ≤ 0 por consiguiente d ∈ S0 (f∞ ).
Se dice que una función f es inf-compacta si Sλ (f ) es compacto ∀ λ. Esto
implica que una función inf-compacto es sci. Una propiedad fundamental
de funciones inf-compactas es la siguiente:
Proposición 2.3.3 Sea f : IRn →] − ∞, +∞] y sea α = inf f (x). Si f es
inf-compacto, entonces α > −∞ y S = {x : f (x) = α} es un compacto no
vacı́o.
T
Demostración. Note que S = λ>α Sλ f . Los Sλ f son compactos encajados no vacı́os, en consecuencia S es un compacto no vacı́o, Sea x̄ ∈ S,
entonces α = f (x̄) > −∞.
Proposición 2.3.4 Sea f convexa sci propia, entonces
f es inf-compacto ⇐⇒ S0 (f∞ ) = {0}
f es inf-compacto ⇐⇒ ∃ λ tal que Sλ (f ) es compacto no vacı́o.
Demostración. Utilizar el teorema anterior y el hecho que un conjunto
convexo cerrado C es compacto si y solo si C∞ = {0}.
Finalmente se da una caracterización de las funciones inf-compacto (no
necesariamente para funciones convexas)
27
Proposición 2.3.5 Sea f : IRn → [−∞, +∞] sci f es inf-compacto ⇐⇒
(kxn k → +∞ ⇒ f (xn ) → +∞)
Demostración. Supongamos que f no es inf-compacto, entonces existe λ
tal que Sλ (f ) es no acotado, es decir ∀ n ∈ IN, ∃ xn ∈ Sλ (f ) con kxn k ≥
n, luego kxn k → +∞ y por tanto limsupf (xn ) ≤ λ. Recı́procamente,
Supongamos que f es inf-compacto y que exista una sucesión kxn k → +∞
con limsupf (xn ) ≤ λ < +∞, xn ∈ Sλ+1 (f ) para n suficientemente grande,
lo cual es imposible ya que Sλ+1 (f ) es acotado.
Proposición 2.3.6 Sean f, g : IRn → [−∞, +∞] f inf-compacto, g sci y
acotada inferiormente( es decir ∃ β > −∞ tal que g(x) ≥ β ∀ x), entonces
f + g es inf-compacto.
Demostración. Observe que f (x) + g(x) ≤ λ ⇒ f (x) + β ≤ λ. En
consecuencia Sλ (f + g) ⊂ Sλ−β (f ) que es acotada. Se sigue que f + g es
inf-compacto.
Una función f es llamada estrictamente convexa si
f (tx + (1 − t)y) < tf (x) + (1 − t)f (y) ∀ t ∈]0, 1[, ∀ x, y; x 6= y
Una función f es llamada fuertemente convexa si
f (tx + (1 − t)y) ≤ tf (x) + (1 − t)f (y) −
α
t(1 − t)kx − yk2 ∀ t ∈ [0, 1]
2
∀ x, y ∈ IRn (k.k norma euclidiana ) α es llamado coeficiente de la convexidad fuerte (coercividad) de f . Una función fuertemente convexa es
estrictamente convexa. Una función estrictamente convexa si alcanza su
ı́nfimo, ella la alcanza en un único punto.
Proposición 2.3.7 Sea f : IRn →] − ∞, +∞] y sea x̄ un punto arbitrario
de IRn . Sea g definida por g(x) = f (x) − α2 kx − x̄k2 . Entonces f es
fuertemente convexa de coeficiente α > 0 si y solo si g es convexa.
28
Demostración. f es fuertemente convexa de coeficiente α si y solo si
∀ t ∈]0, 1[, ∀ x, y ∈ IRn se tiene
α
f (x + t(y − x)) ≤ f (x) + t[f (y) − f (x)] − t(1 − t)kx − yk2
2
esto es si y solo si
α
α
kx + t(y − x) − x̄k2 ≤ g(x) + t[g(y) − g(x)] + tky−
2
2
α
α
x̄k2 + (1 − t)kx − x̄k2 − t(1 − t)kx − yk2
2
2
Es suficiente entonces observar que:
g(x + t(y − x)) +
kx + t(y − x) − x̄k2 = kx − x̄k2 + tky − x̄k2 − tkx − x̄k2 − t(1 − t)kx − yk2
Corolario 2.3.1 Sea f : IRn → IR. Si int(dom(f )) 6= ∅ y f es dos veces
diferenciable sobre sobre C, entonces f es fuertemente convexa de coeficiente de coercividad α > 0 si y solo si h∇2 f (x)d, di ≥ αkdk2 ∀ x ∈
int(dom(f )), ∀d ∈ IRn
Demostración. Defina g(x) = f (x) − α2 kxk2 . Se tiene entonces que para
todo x ∈ int(dom(f )) ∇2 g(x) = ∇2 f (x)−αI, en consecuencia g es convexa
sobre int(dom(f )) si y solo si h∇2 f (x)d, di ≥ αkdk2 ∀ x ∈ int(dom(f )).
Es suficiente de constatar que g es sci.
Teorema 2.3.2 Sea f : IRn → IR convexa sci propia. Si f es fuertemente
convexa, entonces f es inf-compacto.
Demostración. Sea α el coeficiente de la convexidad fuerte de f , x̄ ∈
dom(f ) y g(x) = f (x) − α2 kx − x̄k2 , g es entonces convexa y sci. Sea d 6= 0,
f∞ (d) = sup
t>0
g(x̄ + td) − g(x̄) αt 2
+ |dk .
t
2
g es convexa y en consecuencia
g(x̄ + td) − g(x̄)
g(x̄ + d) − g(x̄)
≥
∀t > 1
t
1
29
y en consecuencia f∞ (d) = ∞ si d 6= 0.
Aplicación. El principio variacional de Ekeland.
Teorema 2.3.3 Sea f : IRn →]−∞, +∞[ diferenciable tal que −∞ < m =
inf f (x). Sea > 0 y sea x tal que f (x ) ≤ m + . Existe entonces x̄ tal
√
√
que kx̄ − x k ≤ , k∇f (x̄)k ≤ 2 y f (x̄) ≤ m + .
Demostración. Consideremos g(x) = f (x) + α2 kx − x k2 con α > 0 f es
sci y la componente x → α2 kx − x k2 es inf-compacto. Se sigue que g es
inf-compacto. En consecuencia existe x̄ tal que g(x̄) ≤ g(x) para todo x,
se sigue que ∇g(x̄) = 0 y en consecuencia ∇f (x̄) + α(x − x ) = 0 y por lo
tanto k∇f (x̄)k = αkx − x k. Por otro lado
m+
α
α
kx − x k2 ≤ f (x̄) + kx − x k2 ≤ f (x ) ≤ m + 2
2
Se tiene por lo tanto kx − x k2 ≤
2
α,
f (x̄) ≤ m + . Tome α = 2.
30
Capı́tulo 3
Conjugación y
Subdiferencial
3.1
Teorema de separación
Se llaman hiperplanos de IRn , a los conjuntos de la forma
H = {x ∈ IRn : ha, xi = α}
donde a ∈ IRn , a 6= 0 y α ∈ IR. Los hiperplanos de IRn son los subespacios afines de dimensión (n − 1). Un hiperplano de R n divide IRn en dos
semiespacios cerrados
E1 = {x ∈ IRn : ha, xi ≥ α}
y
E2 = {x ∈ IRn : ha, xi ≤ α}
Dados S1 , S2 ⊂ R n , S1 y S2 no vacı́os, se habla de:
Separación Si existen a ∈ R n , a 6= 0 y α ∈ R tales que
ha, x1 i ≤ α ≤ ha, x2 i ∀ x1 ∈ S1 y x2 ∈ S2
31
Separación propia Si existe separación y además existen x1 ∈ S1 , x2 ∈
S2 tales que
ha, x2 − x1 i > 0
(S1 y S2 no están contenidos ambos en el hiperplano).
Separación estricta Si existen a ∈ R n , a 6= 0 y α ∈ R tales que
ha, x1 i < α < ha, x2 i ∀ x1 ∈ S1 y x2 ∈ S2
Separación fuerte Si existen a ∈ R n , a 6= 0, α1 ∈ IR y α2 ∈ IR tales que
ha, x1 i ≤ α1 < α2 ≤ ha, x2 i ∀ x1 ∈ S1 y x2 ∈ S2
Ahora analizaremos la separación de conjuntos con intersección vacı́a. Note
que:
S1 ∩ S2 = ∅ si y solo si 0 ∈
/ S2 − S1
Los primeros resultados de separación caracterizan la separación del
origen con un conjunto.
Teorema 3.1.1 Si C ⊂ IRn es un convexo cerrado no vacı́o tal que 0 ∈
/ C,
n
entonces existen a ∈ R y α > 0 tales que ha, xi ≥ α ∀ x ∈ C
Demostración. Consideremos el problema m = inf[||x||2 : x ∈ C] (donde
|| · || es la norma euclidiana). Observe que la función x → kxk2 es fuertemente convexa y en consecuencia convexa y sci. Entonces, existe un único
x̄ en C tal que m = kx̄k2 ≤ kxk2 ∀x ∈ C. Debido a que 0 ∈
/ C, se tiene
que x̄ 6= 0 y en consecuencia m > 0. Luego, ∀x ∈ C y t ∈ [0, 1] se tiene que
kx̄k = m ≤ hx̄ + t(x − x̄), x̄ + t(x − x̄)i = kx̄k2 + 2thx̄, x − x̄i + kx − x̄k2 . Esto
ultimo implica que hx̄, x − x̄i ≥ 0 ∀ x ∈ C. Tomando a = x̄ y α = kx̄k2 se
tiene el resultado.
Teorema 3.1.2 Si C es un convexo no vacı́o tal que 0 ∈
/ C, entonces existe
n
a ∈ R , a 6= 0 tal que ha, xi ≥ 0 ∀ x ∈ C y ha, xi > 0 ∀ x ∈ ri(C) (se tiene
separación propia)
32
Demostración. Si 0 ∈
/ C, entonces separar 0 de C usando el Teorema
3.1.1. Caso contrario, 0 ∈ C en consecuencia 0 ∈ af f (C). Ahora, considere
D = C + [af f (C)]⊥ . Note que D es convexo, 0 ∈
/ D y int(D) = ri(C) +
⊥
[af f (C)] . Sea x̄ ∈ ri(C), entonces x̄ ∈ int(D). Luego, para todo entero
p > 0, − xp ∈
/ D (en caso contrario 0 ∈ (D) ya que x̄ ∈ int(D) y 0 =
1
1
x̄
x̄
x̄
+
(1
−
p+1
p+1 )(− p )). Separando 0 de D + p , tenemos que existen:
ap 6= 0 y αp > 0 tales que
0 < αp ≤ hap , (x +
x̄
)i ∀ x ∈ D
p
Sin perdida de generalidad, se puede suponer kap k = 1. Haciendo x = x̄ se
tiene
1
0 < αp ≤ (1 + )hap , xi ≤ 2kxk
p
Luego, la sucesión {(ap , αp )} es acotada. Sea (a, α) un valor de adherencia
de la sucesión, entonces existe una subsucesión convergente a este valor. Se
tiene kak = 1 y α ≥ 0. Pasando al limite:
0 ≤ α ≤ ha, xi ∀ x ∈ D por lo tanto ∀ x ∈ C
Por otro lado si x ∈ ri(C) entonces x ∈ int(D) y por lo tanto ha, xi > 0.
Teorema 3.1.3 (Separación fuerte) Sean C, D dos convexos cerrados y
no vacı́os tales que:
1. C ∩ D = ∅,
2. d ∈ C∞ ∩ D∞ ⇒ −d ∈ C∞ ∩ D∞
entonces existen a ∈ R n , α1 , α2 ∈ R tales que
ha, xi ≤ α1 < α2 ≤ ha, yi ∀ x ∈ C, ∀y ∈ D
Demostración. Tomando S = D − C, entonces 0 ∈
/ S y S es cerrado, en
consecuencia por el Teorema 3.1.1 existen a ∈ R n y β > 0 tal que
β≤
inf
x∈C,y∈D
ha, y − xi = inf ha, yi − sup ha, xi
y∈D
33
x∈C
Tomando α1 = supx∈C ha, xi y α2 = inf y∈D ha, yi, se tiene α2 − α1 ≥ β >
0.
Teorema 3.1.4 (Separación propia) Sean C, D dos convexos no vacı́os
tales que ri(C) ∩ ri(D) 6= ∅, entonces existen a ∈ R n , a 6= 0 y α ∈ R tales
que
ha, xi ≤ α ≤ ha, yi ∀ x ∈ C, y ∈ D
Además para todo x ∈ ri(C) y y ∈ ri(D) se tiene ha, y − xi > 0
Demostración. Tomando M = ri(D) − ri(C) = ri(M ), se tiene 0 ∈
/M
n
convexo no vacı́o, por el Teorema 3.1.2, existe a ∈ R , a 6= 0 tal que
ha, xi < ha, yi ∀ x ∈ ri(C), y ∈ ri(D)
por lo tanto
sup ha, xi <
inf ha, yi
x∈ri(D)
x∈ri(C)
Luego debido a que
sup ha, xi = sup ha, xi = sup ha, xi
x∈ri(C)
x∈ri(C)
x∈C
y
inf ha, yi =
y∈ri(D)
inf ha, yi = inf ha, yi
y∈ri(D)
y∈D
se tiene el teorema tomando α = 12 [supx∈C ha, xi + infy∈D ha, yi].
Observación, En general no se tiene la existencia de α ∈ R y a ∈ R n tal
que
ha, xi < α < ha, yi ∀ x ∈ ri(C) y y ∈ ri(D)
como contraejemplo considere:
C = {(x, y) : x > 0, y > 0, xy ≥ 1} y D = {(x, y) : y = 0}
34
3.2
Conos polares
Sea K ⊂ R n , K 6= ∅. Definamos
K 0 = {x∗ ∈ R n : hx, x∗ i ≤ 0 ∀ x ∈ K} =
\
{x∗ ∈ R n : hx, x∗ i ≤ 0}
x∈K
K 0 es un cono convexo y cerrado como intersección de conos convexos
cerrados. Es fácil ver que K1 ⊂ K2 implica K10 ⊃ K20 , (K)0 = K 0 ,
[con(K)]0 = K 0 . Existen numerosas propiedades concerniente a los polares tanto de la intersección, reunión, de la suma, etc que son estudiadas
aquı́. Notemos que siempre se tiene K 00 ⊃ K.
Teorema 3.2.1 Sea K un cono convexo cerrado y no vacı́o, entonces
(K 0 )0 = K
Demostración. sea x ∈
/ K, entonces existe a 6= 0 y α ∈ R tal que
ha, xi = α < ha, yi ∀y ∈ K. Debido a que 0 ∈ K se tiene α < 0, luego
como K es un cono h−a, yi ≤ 0 para todo y ∈ K y por lo tanto −a ∈ K 0 ,
de esta manera h−a, xi = −α > 0 y ası́ x ∈
/ K 00 .
Observación, si K = ∅, K 0 = R n y K 00 = {0} aquı́ K 00 6= K. El teorema
nos dice que si K es un cono convexo cerrado no vacı́o este es el polar de su
polar, luego perfectamente definido con K 0 este es la base de la dualidad
convexa.
Corolario 3.2.1 Sea K ∈ R n , K 6= ∅, entonces K 00 es el cono convexo
cerrado mas pequeño conteniendo K.
Demostración. Sea x ∈ K, entonces hx, x∗ i ∀ x∗ ∈ K 0 y por consiguiente
x ∈ K 00 . Se sigue que K 00 es un cono convexo cerrado conteniendo K. Sea
T un cono convexo cerrado conteniendo K, entonces T ⊃ K ⇒ T 0 ⊂ K 0
⇒ T = T 00 ⊃ K 00 . En consecuencia K 00 es el cono convexo cerrado mas
pequeño conteniendo K. Si K es un cono convexo, K es el cono convexo
cerrado mas pequeño conteniendo K.
35
3.3
Funciones conjugadas
3.3.1
Introducción geométrica
Sea f una función convexa sci propia, epi(f ) es un convexo cerrado de
R n+1 . Considere
K = {(kx, kλ, −k) : k ≥ 0, (x, λ) ∈ epi(f )}
el cono generado por epi(f )×{−1} en R n+2 este es convexo porque epi(f )×
{−1} es convexo. K no es necesariamente cerrado, de hecho, K difiere de
su clausura solo en el subespacio R n × R × {0}. Se tiene:
\
K (R n × R × {−1}) = epi(f ) × {−1}
Consideremos K 0 , este es un cono convexo cerrado. En efecto
K 0 = {(x∗ , λ∗ , µ∗ ) : hx, x∗ i + λλ∗ − µ∗ ∀ x ∈ dom(f ), ∀ λ ≥ f (x)}
Sea x ∈ dom(f ), haciendo variar λ en [f (x), +∞[ se ve que necesariamente
se debe tener λ∗ ≤ 0 si (x∗ , λ∗ , µ∗ ) ∈ K 0 . Sea T = {(x∗ , µ∗ ) : (x∗ , −1, µ∗ ) ∈
K 0 }. T es convexo cerrado. Además µ∗1 ≤ µ∗2 y (x1 , µ∗1 ) ∈ T ⇒ (x1 , µ∗1 ) ∈
T por lo tanto T es el epı́grafo de una función convexa cerrada que se
denotará por f ∗ . Se tiene:
f ∗ (x∗ ) = Inf [µ∗ : hx, x∗ i − λ ≤ µ∗ ∀ x ∈ dom(f ), ∀ λ ≥ f (x)]
es decir
f ∗ (x∗ ) =
sup
[hx, x∗ i − f (x)]
x∈dom(f )
Además se puede mostrar que
K 0 = {(kx∗ , −k, kµ∗ ) : k ≥ 0, (x∗ , µ∗ ) ∈ epi(f ∗ )}
Debido a que K y K 0 se corresponden por dualidad, se sigue que f y f ∗
se corresponden por dualidad. Cuando uno de ellos es conocido, entonces
el otro también es conocido.
36
3.3.2
Definición
Sea f : R n → R, se llama conjugación (en el sentido de Fenchel) a la función
siguiente:
f ∗ (x∗ ) =
sup
[hx, x∗ i − f (x)] = sup[hx, x∗ i − f (x)]
x
x∈dom(f )
(porque f (x) = +∞ si x ∈
/ dom(f )). Observemos que la función x →
hx, x∗ i − f (x) es convexa y sci en consecuencia f ∗ es siempre convexa y sci
como un supremo de funciones convexas y sci.
• si existe x0 tal que f (x0 ) = −∞, entonces f ∗ (x∗ ) ≥ hx, x∗ i − f (x0 ) =
+∞ en consecuencia f ∗ (x∗ ) = +∞ ∀ x∗
• si f (x) = +∞ ∀ x, entonces f ∗ (x∗ ) = −∞ ∀ x∗
• si f (x) ≤ g(x) ∀ x, entonces f ∗ (x∗ ) ≥ g ∗ (x∗ ) ∀ x∗
• f ∗ (x∗ ) + f (x) ≥ hx, x∗ i ∀ x, ∀ x∗ .
Dada f : IRn → IR definamos:
fc (x) = inf[λ : (x, λ) ∈ co(epi(f ))]
fc (x) = inf[λ : (x, λ) ∈ co(epi(f ))]
Las dos funciones son respectivamente la función convexa mas grande mayorada por f , la función convexa sci más grande mayorada por f .
Denotaremos por f a la función sci mas grande mayorada por f , esto es:
f (x) = inf [λ : (x, λ) ∈ epi(f )]
Proposición 3.3.1
f ∗ = (f )∗ = (fc )∗ = (fc )∗
Demostración. f ∗ (x∗ ) = sup[hx, x∗ i − λ : f (x) ≤ λ] pero
hx, x∗ i − λ ≤ µ∗
37
∀(x, λ) ∈ epi(f )
m
hx, x∗ i − λ ≤ µ∗ ∀(x, λ) ∈ epi(f )
m
hx, x∗ i − λ ≤ µ∗ ∀(x, λ) ∈ co(epi(f ))
hx, x∗ i − λ ≤ µ∗ ∀(x, λ) ∈ co(epi(f ))
Proposición 3.3.2
f ∗∗ (x) = sup inf [hx − y, x∗ i + f (y)]
x∗
y
y
f ∗∗ (x) ≤ f (x) ∀ x
Demostración.
f ∗∗ (x) = sup[hx, x∗ i − f ∗ (x∗ )] = sup[hx, x∗ i − sup[hy, x∗ i − f (y)]]
x∗
x∗
y
de donde
f ∗∗ (x) = sup inf [hx − y, x∗ i + f (y)]
x∗
y
En particular
f ∗∗ (x) ≤ sup[hx − x, x∗ i + f (y)] = f (x)
x∗
Teorema 3.3.1 Sea f una función convexa sci propia, entonces f ∗ es convexa sci y propia y f ∗∗ = f
Demostración. Nosotros sabemos que f ∗∗ (x) ≤ f (x) para todo x. Para
probar la recı́proca, sea λ0 < f (x0 ). Entonces (x0 , λ0 ) no pertenece al
epi(f ). Por el teorema de separación fuerte, existe (x∗0 , λ∗0 ) and α0 > 0
such that
hx∗0 , x0 i + λ∗0 , λ0 ≥ hx∗0 , xi + λ∗0 , λ + α0 ∀(x, λ) ∈ epi(f )
38
(3.1)
Fijemos x ∈ dom(f ) y sea λ ∈ [f (x), +∞[, la equación 3.1 implica que
λ∗0 ≤ 0.
Caso 1: λ∗0 < 0 Sin pérdida de generalidad, asumamos que λ∗0 = −1. De
la ecuación 3.1, cuando λ = f (x) y x ∈ dom(f ) se tiene que:
hx∗0 , x0 i − λ0 ≥ hx∗0 , xi − f (x) + α0 ∀x ∈ dom(f )
hx∗0 , x0 i − λ0 ≥ f ∗ (x∗0 ) + α0
finalmente
f ∗∗ (x0 ) ≥ hx∗0 , x0 i − f ∗ (x∗0 ) ≥ α0 + λ0
La desigualdad ocurre para todo λ0 < f (x0 ). Ası́, f ∗∗ (x0 ) ≥ f (x0 ).
Caso 2: λ∗0 = 0 En este caso la equación 3.1 se reduce a:
hx∗0 , x0 i ≥ hx∗0 , xi + α0 ∀x ∈ dom(f )
sin pérdida de generalidad podemos asumir que α0 = 1. Entonces
hx∗0 , x0 i ≥ hx∗0 , xi + 1 ∀x ∈ dom(f )
(3.2)
En este caso x0 ∈
/ dom(f ).
Tomemos x1 ∈ dom(f ) and λ1 < f (x1 ). De forma similar (porque
(x1 , λ1 ) ∈
/ epi(f )), existen (x∗1 , λ1 ) ∈ R n+1 y α1 > 0 tal que
hx∗1 , x1 i − λ1 ≥ hx∗1 , xi − f (x) + α1
(3.3)
combinando las ecuaciones 3.2 y 3.3, tenemos que ∀µ > 0:
hx∗1 , x1 i − λ1 + hµx∗0 , x0 i ≥ hx∗1 + µx∗0 , xi − f (x) + α1 + µ ∀x ∈ dom(f )
luego
hx∗1 + µx∗0 , x0 i + hx∗1 , x1 − x0 i − λ1 ≥ f ∗ (x∗1 + µx∗0 ) + α1 + µ
f ∗∗ (x∗0 ) ≥ hx∗1 + µx∗0 , x0 i − f ∗ (x∗1 + µx∗0 ) ≥ α1 + µ + λ1 + hx∗1 , x0 − x1 i
esta ultima desigualdad ocurre para todo µ > 0. Ası́ f ∗∗ (x∗0 ) = +∞.
39
En ambos casos f (x0 ) = f ∗∗ (x0 ).
Corolario 3.3.1
a) f ∗∗∗ = f ∗
b) Si f convexa propia, entonces f ∗∗ = f
Demostración.
a) f ∗ es siempre convexa sci. Si f ∗ (x∗0 ) = −∞, entonces dom(f ) = y
por lo tanto f ∗ (x∗ ) = −∞ ∀x∗ , luego f ∗∗ (x) = +∞ ∀x y f ∗∗∗ (x∗ ) =
−∞ ∀x∗ . Si dom(f ∗ ) =, entonces f ∗∗ (x) = −∞ ∀x y f ∗∗∗ (x∗ ) = +∞
∀x∗ . En los otros casos f es convexa propia y f = f ∗∗ y f ∗∗∗ = f ∗ .
b) Si f es convexa y propia, entonces f es convexa y propia. De otro
lado, f ∗ = (f )∗ y en consecuencia f ∗∗ = (f )∗∗ = f .
Observación, Si f es convexa sci pero no propia, se puede tener que
f 6= f ∗∗
Ejemplo.
(
−∞ si x ≤ 0
f (x) =
+∞
si x > 0
entonces
f ∗ (x∗ ) = +∞ ∀x∗ y por lo tanto f ∗∗ (x) = −∞ ∀ x
Por último se tiene
f ∗∗ (x) = sup[hx, x∗ i − f ∗ (x∗ ) = sup[hx, x∗ i − sup[hy, x∗ i − f (y)]]
x∗
x∗
y
y por lo tanto
f ∗∗ (x) = sup inf [hx − y, x∗ i + f (y)]
x∗
y
Bajo esta formula se ve inmediatamente que f ∗∗ (x) ≤ f (x) ∀x. Por otro
lado debido a que f ∗ = (fc )∗ , se tiene f ∗∗ = (fc )∗∗ . Debido a que fc es
convexa sci se sigue que si fc (o f ∗∗ ) es propia, entonces f ∗∗ = fc . En este
caso f ∗∗ es la mas grande minorante convexa sci de f
40
3.4
Funciones indicatriz y soporte de un conjunto
(
n
Sea C ⊂ IR , C 6= ∅ definamos δ(x|C) =
0
+∞
si x ∈ C
si x ∈
/C
δ(.|C) es llamado función indicatriz de C Se ve inmediatamente que:
C es convexo ⇐⇒ δ(.|C) es convexa
C es cerrado ⇐⇒ δ(.|C) es sci
S ⊂ C ⇐⇒ δ(.|S) ≥ δ(.|T ) ∀x
Por otro lado δ(.|S), δ(.|co(S)) y δ(.|coS) son respectivamente las mas
grandes funciones sci la mas grande función convexa y la mas grande función
convexa sci
La función conjugación de la función indicatriz de C es llamada función
soporte de C. Se tiene entonces
δ ∗ (x∗ |C) = sup[hx, x∗ i − δ(x|C)] = supx∈C hx, x∗ i
x
∗
Si C 6= ∅, entonces δ (.|C) es convexa sci y propia.
Por otro lado se ve que δ ∗ (kx∗ |C) = kδ ∗ (x∗ |C) ∀k > 0, ∀x∗ se dice entonces
que δ ∗ (.|C) es positivamente homogénea (de grado 1). Recı́procamente se
tiene:
Teorema 3.4.1 Sea f convexa sci propia y positivamente homogénea de
grado 1, entonces existe C convexa cerrada y no vacı́o tal que f (x∗ ) =
δ ∗ (x∗ |C) ∀x∗ además f ∗ (x) = δ(x|C) ∀x
Demostración.
a) f ∗ (x) = supx∗ [hx, x∗ i − f (x∗ )] = supx∗ ,k>0 [hx, kx∗ i − f (kx∗ )], pero
se sabe que f (kx∗ ) = kf (x∗ ) si k > 0, por lo tanto
f ∗ (x) = sup[k[sup[hx, x∗ i − f (x∗ )]]]
k>0
x∗
41
Puesto que f es propia, notamos que siempre supx∗ [hx, x∗ i−f (x∗ )] >
−∞. Si supx∗ [hx, x∗ i − f (x∗ )] ≤ 0, entonces f ∗ (x) = 0, en caso
contrario f ∗ (x) = +∞. En consecuencia f ∗ solo toma los valores
0 o +∞. Sea C = S0 (f ∗ ). C es un conjunto convexo cerrado y
f ∗ (x) = δ(x|C) ∀x
b) Debido a que f es convexa sci y propia, se tiene f = f ∗∗ y en consecuencia f (x∗ ) = δ ∗ (x∗ |C).
Sea C un conjunto no vacı́o, Se llama cono barrera de C al conjunto K
definido por
K = {x∗ : δ ∗ (x∗ |C) < +∞} = dom(δ ∗ (.|C))
Es fácil ver que K es un cono, K es convexa como dominio de una función
convexa, en general K no es cerrado aun cuando C es convexo cerrado. Por
ejemplo considere: C = {(x, y) ∈ IR2 : y + ex ≤ 0} es un convexo cerrado.
Calculándose δ ∗ (.|C) se verifica que K no es cerrado.
Teorema 3.4.2 Sea C convexa cerrada y no vacı́o y K su cono barrera,
entonces K ⊂ (C∞ )0 y K 0 = C∞ .
Demostración. Sea a ∈ C
i) Sea x∗ ∈ K, entonces δ ∗ (x∗ |C) < +∞. En particular si d ∈ C∞ se
tiene ha + λd, x∗ i ≤ δ ∗ (x∗ |C) ∀λ > 0. Por consiguiente hd, x∗ i ≤ 0
∀d ∈ C∞ y por lo tanto x∗ ∈ (C∞ )0 , de esta manera K ⊂ (C∞ )0 . Por
dualidad K 0 ⊃ (C∞ )00 = C∞ debido a que C∞ es un cono convexo
cerrado no vacı́o.
ii) Sea d ∈
/ C∞ entonces existe λ > 0 tal que a + λd ∈
/ C. Se separa
∗
a + λd de C. Existe x =
6 0 tal que
ha + λd, x∗ i > hx, x∗ i ∀x ∈ C.
Haciendo x = a ∈ C, se tiene hd, x∗ i > 0. Por otro lado x∗ ∈ K por
que
sup[hx, x∗ i : x ∈ C] < ha + λd, x∗ i
42
Por lo tanto d ∈
/ K 0.
Corolario 3.4.1 Un convexo es acotado si y solo si su cono barrera = IRn
Demostración. C es acotado ⇐⇒ C es acotado ⇐⇒ (C)∞ = {0} ⇐⇒
K = IRn porque los conos barrera de C y C son los mismos. Por último se
notara que las funciones soportes de un conjunto y de su envoltura convexa
cerrada son los mismos.
3.5
Función ası́ntota y conjugación
Proposición 3.5.1 Sea f convexa sci propia, entonces f∞ es la función
soporte de del dom(f ∗ ) es decir f∞ (d) = δ ∗ (d|dom(f ∗ ))
(a)
Demostración. Sea a ∈ dom(f ), entonces f∞ (d) = supt>0 f (a+td)−f
t
∗
∗ ∗
∗∗
pero f (a + td) = supx∗ ∈dom(f ∗ ) [hx , a + tdi − f (x )] pero f = f y por lo
tanto
1 ∗
f∞ (d) =
sup
[hx , a + tdi − f ∗ (x∗ ) − f (a)]
t>0,x∗ ∈dom(f ∗ ) t
f∞ (d) =
sup
x∗ ∈dom(f ∗ )
1
[hx∗ , di + sup (hx∗ , ai − f ∗ (x∗ ) − f (a))]
t>0 t
pero siempre se tiene hx∗ , ai ≤ f ∗ (x∗ ) + f (a) en consecuencia
f∞ (d) = δ ∗ (d|dom(f ∗ ))
Corolario 3.5.1 Sea f convexa sci propia sobre IRn , entonces
f inf-compacto ⇐⇒ 0 ∈ int(dom(f ∗ ))
f ∗ inf-compacto ⇐⇒ 0 ∈ int(dom(f ))
43
Demostración.
(
f inf-compacto ⇐⇒ f∞ (d) =
0
>0
si d = 0
en caso contrario
⇐⇒ 0 ∈ int(dom(f ∗ ))
La otra equivalencia es por dualidad.
El resultado siguiente es muy usado para algunas aplicaciones
Sea f convexa sci propia, pongamos
(
0
si f ∗ (x∗ ) + λ∗ ≤ 0
∗
∗
ψ(x , λ ) =
+∞ en caso contrario
Entonces ψ es convexa sci y propia ( esta es una función indicatriz)
Calculemos ψ ∗
ψ ∗ (x, λ) = sup [hx, x∗ i + λλ∗ : f ∗ (x∗ ) + λ∗ ≤ 0]
x∗ ,λ∗
Si λ < 0, entonces ψ ∗ (x, λ) = ∞ (tomando x∗ ∈ dom(f ∗ ) y haciendo
λ∗ → −∞)
Si λ = 0, entonces ψ ∗ (x, λ) = sup[hx, x∗ i : x∗ ∈ dom(f ∗ )] = f∞ (x)
Si λ > 0, entonces ψ ∗ (x, λ) = supx∗ [hx, x∗ i − λf ∗ (x∗ )] = λ supx∗ [h λx , x∗ i −
f ∗ (x∗ )] = λf ( λx )
Poniendo ϕ = ψ ∗ , el resultado puede ser establecido como:
Dada f convexa sci propia positivamente homogénea, definiendo la función
ϕ
x
λf ( λ ) si λ > 0
ϕ(x, u) =
f∞ (x) si λ = 0
+∞
si λ < 0
entonces su conjugada es ϕ∗ = ψ ∗∗ = ψ en consecuencia
(
0
si f ∗ (x∗ ) + λ∗ ≤ 0
∗ ∗
∗
ϕ (x , λ ) =
+∞ en caso contrario
44
3.6
Subdiferencial de una función convexa
Sea f convexa propia sobre IRn , a ∈ dom(f ), se dice que
x∗ ∈ ∂f (a) ⇐⇒ f (a) + f ∗ (x∗ ) = hx∗ , ai
(3.4)
recordemos que hx∗ , ai ≤ f ∗ (x∗ )+f (a) siempre es satisfecho, en consecuencia
x∗ ∈ ∂f (a) ⇐⇒ f (a) + f ∗ (x∗ ) ≤ hx∗ , ai
(3.5)
y debido a que f ∗ (x∗ ) = supx [hx∗ , xi − f (x)]
x∗ ∈ ∂f (a) ⇐⇒ f (a) + hx∗ , x − ai ≤ f (x) ∀x
(3.6)
Note que
0 ∈ ∂f (a) ⇐⇒ f (a) = inf f (x)
Interpretación geométrica
Sea
H = {(x, λ) : f (a) + hx∗ , x − ai = λ}
H es hiperplano de IRn ,(3.6, 3.4) significa que el epı́grafo de f esta situado
enteramente encima del hiperplano ∂f (a) es llamado el subdiferencial (sub
gradiente) de f en a
Proposición 3.6.1 ∂f (a) es un convexo cerrado
Demostración. ∂f (a) = {x∗ : f ∗ (x∗ ) − ha, x∗ i ≤ −f (a)}. Pero la aplicación x∗ → f ∗ (x∗ ) − ha, x∗ i es convexa sci
Proposición 3.6.2 Sea f convexa propia sobre IRn , sea a ∈ dom(f ). Si
∂f (a) 6= ∅ entonces f es sci en a
Demostración. Sea x∗ ∈ ∂f (a), f (a) + hx∗ , x − ai ≤ f (x) ∀x. Sea
λ < f (a), existe V ∈ ϑ(a) tal que x ∈ V ⇒ λ < f (a) + hx∗ , x − ai ≤ f (x)
porque la aplicación x → f (a) + hx∗ , x − ai es continua , entonces f es sci
en a.
45
Observación, La recı́proca es falsa: Considerar f : IR →] − ∞, +∞] con
(
+∞ si x < 0,
√
f (x) =
− x si x ≥ 0.
f es convexa sci y
∗
∗
∗
f (x ) = sup[xx +
√
(
x] =
x≥0
+∞ si x∗ ≥ 0
− 4x1∗ si x∗ < 0
√
entonces se tiene x∗ ∈ ∂f (x) ⇐⇒ − x − 4x1∗ = x∗ x, x ≥ 0 y x∗ < 0.
Entonces
(
1
{− 2√
}
si x > 0
x
∂f (x) =
∅
en caso contrario
Por lo tanto 0 ∈ dom(f ) y f sci en 0.
Proposición 3.6.3 Sea f convexa sci propia, entonces x∗ ∈ ∂f (x) ⇐⇒
x ∈ ∂f ∗ (x∗ ).
Demostración. En efecto f = f ∗∗ , utilizar la definición de ∂f .
Teorema 3.6.1 Sea f convexa sci y propia, entonces ∂f (a) 6= ∅ ∀a ∈
ri(dom(f )).
Demostración. Definamos C = {a} × {f (a)}. Entonces C = ri(C) y
C ∩ ri(epi(f )) = ∅. Entonces existe (x∗ , α∗ ) 6= (0, 0) tal que
ha, x∗ i + α∗ f (a) > hx, x∗ i + α∗ λ ∀(x, λ) ∈ ri(epi(f ))
(3.7)
Pero (a, λ) ∈ ri(epi(f )) ∀λ > f (a), entonces α∗ < 0. Sin perdida de
generalidad consideremos α∗ = −1. Luego de la ecuación 3.7 tenemos que
ha, x∗ i − f (a) ≥ hx, x∗ i − f (x) ∀x ∈ dom(f )
ası́ ha, x∗ i − f (a) ≥ f ∗ (x∗ ). Esto implica que x∗ ∈ ∂f (a).
46
3.7
Derivadas direccionales de una función
convexa
Sea f : IRn → [−∞, +∞] finita en a. Se llama derivada direccional de f en
a en la dirección de d, y denotado por f 0 (a, d) al limite siguiente si si este
existe
f (x + td) − f (a)
f 0 (a, d) = lim
t→0,t>0
t
Teorema 3.7.1 Sea f convexa propia y sea a ∈ dom(f ), entonces
a)
f 0 (a, d) = inf
t>0
f (x + td) − f (a)
t
(en consecuencia f 0 (a, d) existe con eventualmente f 0 (a, d) = +∞ o
−∞)
b) f 0 (a, .) es una función convexa positivamente homogénea.
Demostración.
(a)
es creciente
a) debido a que f es convexa, la función t → f (x+td)−f
t
f (x+td)−f (a)
0
sobre ]0, +∞[, en consecuencia f (a, d) = inf t→0+
t
b) Se ve trivialmente que f 0 (a, kd) = kf 0 (a, d) ∀k > 0
Por otro lado la función g(d) = f (a+d)−f (a) es convexa, entonces ϕ(d, θ) =
θg( dθ ) = θ[f (a + dθ ) − f (a)] es convexa sobre IRn ×]0, +∞[. Se sigue que
f 0 (a, d) es convexa en d debido a que f 0 (a, d) = inf θ>0 ϕ(d, θ).
Proposición 3.7.1 Sea f convexa, propia, a ∈ dom(f ), entonces
x∗ ∈ ∂f (a) ⇐⇒ f 0 (a, d) ≥ hx∗ , di ∀d ∈ IRn .
Demostración. Sea x∗ ∈ ∂f (a), entonces f (a + td) − f (a) ≥ thx∗ , di ∀d ∈
IRn , ∀t > 0. Dividiendo por t y luego pasando al limite, f 0 (a, d) ≥ hx∗ , di.
Mostraremos que si f 0 (a, d) ≥ hx∗ , di ∀d entonces x∗ ∈ ∂f (a). Es suficiente
probar que hx∗ , x − ai ≤ f (x) − f (a) ∀x. En efecto, tomando d = x − a se
47
tiene hx∗ , x − ai ≤ f 0 (a, d) ≤
el resultado.
f (x+td)−f (a)
t
∀t > 0, haciendo t = 1 se tiene
Proposición 3.7.2 Sea f convexa propia y a ∈ dom(f )
a) Si existe d tal que f 0 (a, d) = −∞ entonces ∂f (a) = ∅.
b) Si f 0 (a, d) > −∞ ∀d, entonces θ(d) = δ ∗ (d|∂f (a)) donde θ es la
función θ(d) = f 0 (a, d) ∀d. Se sigue que ∂f (a) 6= ∅.
Demostración.
a) Si f 0 (a, d) = −∞, debido a que hx∗ , x − ai ≤ f 0 (a, d) ∀x∗ ∈ ∂f (a), se
tiene que ∂f (a) = ∅.
b) θ es convexa positivamente homogénea y θ también es convexa y
positivamente homogénea. Ası́ θ es la función soporte de un conjunto
convexo cerrado D 6= ∅. Sea µx∗ (d) = f 0 (x, d) − hx∗ , di entonces
µx∗ (d) = θ(d) − hx∗ , di se sigue que
x∗ ∈ ∂f (a) ⇐⇒ µx∗ (d) ≥ 0 ∀d ⇐⇒ µx∗ (d) ≥ 0 ∀d
es decir
x∗ ∈ ∂f (a) ⇐⇒ hx∗ , di ≤ δ ∗ (x∗ |D) ∀d
⇐⇒ sup[hx∗ , di − δ ∗ (x∗ |D)] ≤ 0 ⇐⇒ δ ∗ (x∗ |D) ≤ 0 ⇐⇒ x∗ ∈ D
d
en consecuencia ∂f (a) 6= ∅ y θ(d) = δ ∗ (d|∂f (a)).
Observación, f convexa, sci en a y ∂f (a) 6= ∅ 6=⇒ f 0 (a, .) sci
Ejemplo.
f (x, y) =
y
0
+∞
si y < 0
si x = y = 0
en caso contrario
luego
(
∗
∗
∗
f (x , y ) =
si x∗ = 0 y y ∗ ≥ 1
en caso contrario
0
+∞
48
∂f (0, 0) = {0} × [1, ∞[
θ(1, 0) = f 0 ((0, 0), (1, 0)) = +∞
pero
θ(1, 0) = sup[1x∗ + 0y ∗ : (x∗ , y ∗ ) ∈ ∂f (0, 0)] = 0
Proposición 3.7.3 Sea f convexa propia, a ∈ dom(f ) entonces
∂f (a) 6= ∅ y compacto ⇐⇒ a ∈ int(dom(f ))
En tal caso
f 0 (a, .) = δ ∗ (.|∂f (a))
Demostración.
a) Supongamos que a ∈ int(dom(f )), y sea d ∈ IRn , d 6= 0, entonces
existe t > 0 tal que a + td ∈ dom(f ). Pero
θ(d) = f 0 (a, d) = inf
t>0
f (a + td) − f (a)
≤ f (a + d) − f (a)
t
y en consecuencia f 0 (a, d) = θ(d) < +∞ ∀d ∈ IRn . θ convexa =⇒ 0 =
θ(0) ≤ 12 θ(d) + 12 θ(−d) < +∞. Se sigue que θ(d) > −∞ ∀d. Por lo
tanto θ es una función convexa propia y dom(θ) = IRn , θ es entonces
continua sobre int(dom(f )) = IRn y por consiguiente θ = θ de esta
manera f 0 (a, d) = δ ∗ (d|∂f (a)) < +∞ ∀d. Por consiguiente ∂f (a) es
acotado y por lo tanto compacto.
b) Supongamos que ∂f (a) es compacto. Sea e1 , ..., en los vectores de la
base canónica. Se observa que dom(θ) = IRn , ya que dom(θ) = IRn
en consecuencia θ = θ. Debido a que f 0 (a, ei ) y f 0 (a, −ei ) son finitas
existen ti > 0 y t0i > 0 tal que f (a + ti ei ) y f (a − ti ei ) son < +∞
por consiguiente a + ti ei y a − t0i ei ∈ dom(f ). Observemos que la
envoltura convexa de los 2n puntos a + ti ei , a − t0i ei es una vecindad
de 0 contenido en el dom(f ).
Corolario 3.7.1 Sea f convexa propia, a ∈ ri(dom(f )) entonces ∂f (a) 6=
∅ y f 0 (a, d) = δ ∗ (d|∂f (a))
49
Demostración. Considere IRn = [af f (dom(f ))] × [af f (dom(f ))]⊥ . Definamos f˜ como la restricción de f a af f (dom(f )). Se tiene que
(
fe(x) si y = 0
f (x, y) =
+∞
en caso contrario
entonces
∂f (a1 , a2 ) = ∂ fe(a1 ) × [af f (dom(f ))]⊥
3.8
Derivadas de una función convexa
Sea f : IRn → IR finita en a. Se dice que f es Fréchet-diferenciable en a si
existe x∗ ∈ IRn tal que
f (a + h) − f (a) − hh, x∗ i
→0
khk
cuando h → 0.
Notamos que la definición no depende de la norma in IRn y que el elemento
x∗ (si existe) es único. Entonces ponemos x∗ = ∇f (a) que es llamado la
derivada de Frechet en a. De manera trivial se tiene :
h∇f (a), hi = f 0 (a, h) ∀h si ∇f (a) existe
Teorema 3.8.1 Sea f una función convexa propia y a ∈ dom(f ). Entonces f es Frechet diferenciable en a ⇐⇒ ∂f (a) es un singleton. En este
caso a ∈ int(dom(f )) y ∂f (a) = {∇f (a)}.
Demostración.
a) f Frechet-diferenciable en a ⇒ f 0 (a, h) = h∇f (a), hi∀h. Si x∗ ∈
∂f (a), entonces hx∗ , hi ≤ f 0 (a, h) ≤ h∇f (a), hi∀h, y entonces hx∗ −
∇f (a), hi ≤ 0 ∀h. Haciendo h = x∗ − ∇f (a) se tiene x∗ = ∇f (a).
50
b) Se supone que ∂f (a) = {x∗ } entonces ∂f (a) es un compacto y a ∈
int(dom(f )). Se pone g(x) = f (x) − f (a) − hx − a, x∗ i, entonces g es
convexa y g(a) = 0.
g 0 (a, h) = 0 ∀h
Sea (e1 , e2 , ..., en ) la base canónica de R n , se pone di = ei , dn + i =
−ei ∀i = 1, 2, ..., n. Sea h ∈ R n , se pone ξi = 0, ξn + i = −hi si
hi < 0 y ξi = hi , ξn + i = 0 si hi ≥ 0. Entonces se tiene h =
P2n
Pn
ξi
i=1 ξi di . se considera la norma khk1 = P i=1 |hi | y sea ti = khki
para i = 1, 2, ..., 2n. Entonces ti ≥ 0 ∀i y
ti = 1. Por convexidad
P2n
P2n
de g se tiene g(a + h) = g(a + i=1 ti khk1 di ) ≤ i=1 ti g(a + khk1 di ).
P
2n
g(a+khk1 di )−g(a)
Entonces 0 ≤ g(a+h)−g(a)
≤
. La primera
i=1 ti
khk1
khk1
desigualdad viene del hecho de que g(a + h) ≥ g(a) ∀h. Ya que
g 0 (a, di ) = 0. Y pasando al limite se ve que
lim
h→0
g(a + h) − g(a)
=0
khk1
y entonces ∇g(a) = 0. Por consiguiente x∗ = ∇f (a).
Proposición 3.8.1 Sea f convexa sci propia. Si f es estrictamente convexa, entonces int(dom(f ∗ )) 6= ∅, f ∗ es diferenciable sobre int(dom(f ∗ )) y
∂f ∗ (x∗ ) = ∅ si x∗ ∈
/ int(dom(f ∗ )).
Demostración.
x ∈ ∂f ∗ (x∗ ) ⇒ x es solución optimal de inf x f (x) −
∗
hx, x i. La función f es estrictamente convexa, la solución optimal, si
existe, es única, entonces ∂f ∗ (x∗ ) es un singleton cada vez que ∂f ∗ (x∗ ) 6= ∅.
Pero ∂f ∗ (x∗ ) 6= ∅ si x∗ ∈ ri(dom(f ∗ )), entonces f ∗ es diferenciable sobre
ri(dom(f ∗ )) 6= ∅, f ∗ diferenciable en x∗ ⇒ x∗ ∈ int(dom(f ∗ )). Si x∗
pertenece a la frontera del dom(f ∗ ) entonces ∃d 6= 0 tal que x∗ + td ∈
/
dom(f ∗ ) ∀t > 0, pero entonces f 0∗ (x∗ , d) = +∞, ∂f ∗ (x∗ ) es no acotado o
vacı́o. Pero, si no es vacı́o, es acotado porque es reducido a un punto.
Proposición 3.8.2 Sea f convexa sci propia. Si f ∗ es diferenciable en
todo x∗ tal que ∂f ∗ (x∗ ) 6= ∅, entonces f es estrictamente convexa sobre
ri(dom(f )).
51
Demostración. Supongamos que f no es estrictamente convexa sobre
ri(dom(f )), entonces ∃x, y ∈ ri(dom(f )) y t ∈]0, 1[ tal que x 6= y y
f (tx + (1 − t)y) = tf (x) + (1 − t)f (y)
(3.8)
Porque tx + (1 − t)y ∈ ri(dom(f )), ∃x∗ ∈ ∂f (tx + (1 − t)y) y entonces
f (tx + (1 − t)y) + hx − tx − (1 − t)y, x∗ i ≤ f (x)
(3.9)
f (tx + (1 − t)y) + hy − tx − (1 − t)y, x∗ i ≤ f (y)
(3.10)
Multiplicamos (3.9) por t y (3.10) por (1 − t) y sumando se tiene
f (tx + (1 − t)y) ≤ tf (x) + (1 − t)f (y)
Por la ecuación (3.8), se tiene necesariamente la igualdad en (3.9) y (3.10).
Por otro lado
f (tx + (1 − t)y) + f ∗ (x∗ ) = htx + (1 − t)y, x∗ i
(3.11)
Reemplazando en (3.9) y (3.10) se tiene
f ∗ (x∗ ) + f (x) = hx, x∗ i y f ∗ (x∗ ) + f (y) = hy, x∗ i
y entonces x, y ∈ ∂f ∗ (x∗ ). Lo que es imposible porque ∂f ∗ (x∗ ) o es vacı́o
o es reducido a un punto.
3.9
Subdiferencial de la suma de dos
funciones convexas
Para completar, nosotros solo enunciaremos el siguiente Teorema. La demostración de este Teorema será dada en el siguiente capı́tulo.
Teorema 3.9.1 Sea f y g dos funciones convexas sci propias, s = f + g,
T
a ∈ dom(s) = [dom(f )] [dom(g)] tal que ∂f (a) 6= ∅ y ∂g(a) 6= ∅. Entonces
a) ∂f (a) + ∂g(a) ⊂ ∂s(a)
T
b) Si int(dom(f )) int(dom(g)) 6= ∅, entonces ∂f (a) + ∂g(a) = ∂s(a)
52
Capı́tulo 4
Introducción a la
Dualidad Convexa
4.1
Esquema General
Los problemas de Optimización se presentan, en general, bajo la forma
α = inf [fe(x) : x ∈ C]
donde C ⊂ R n
Considerando f : X → R ∪ {+∞} definida por:
(
fe(x) si x ∈ C
f (x) =
+∞
si x 6∈ C
obtenemos un problema equivalente en el que ya no aparecen las restricciones,
α = inf[f (x) : x ∈ X]
(P )
nosotros llamaremos a (P) problema primal.
Definamos una función ϕ : R n × R p → R verificando la propiedad
ϕ(x, 0) = f (x)
53
∀x ∈ R n
La función ϕ será llamada función de perturbación y denotaremos por u a
la variable de pertubación.
La función h : R p → R definida por:
h(u) = infn ϕ(x, u)
x∈R
es llamada función marginal. Observe que:
α = h(0) = infn ϕ(x, 0) = infn f (x)
x∈R
x∈R
∗∗
Considerando ahora h , la biconjugada de h, se tiene que:
h∗∗ (0) ≤ h(0) = α
donde
h∗∗ (0) = sup[h0, u∗ i − h∗ (u∗ ) : u∗ ∈ R n ]
Luego, haciendo −β = h∗∗ (0), tenemos que:
β = inf n h∗ (u∗ )
(Q)
u∗ ∈R
(Q) es llamado problema dual de (P ) y en general se tiene que −β ≤ α. El
intervalo [−β, α] es llamado salto de dualidad. Obviamente no existe salto
de dualidad si h∗∗ (0) = h(0).
Por otro lado, sabemos que:
h∗ (u∗ ) = sup [hu, u∗ i − h(u)] = sup [hu, u∗ i − infn ϕ(x, u)]
u∈R
∗
∗
n
h (u ) =
u∈R
n
x∈R
∗
[h0, xi + hu, u i − ϕ(x, u)]
sup
(x,u)∈R ×R
n
n
h∗ (u∗ ) = ϕ∗ (0, u∗ )
Denotando por k(x∗ ) = inf u ϕ∗ (x∗ , u∗ ), se tiene que β = k(0).
Ahora observe la simetrı́a entre los dos problemas:
β = inf h∗ (u∗ )
(Q)
ϕ (0, u ) = h∗ (u∗ ) ∀ u∗ ∈ U ∗
k(x∗ ) = inf u∗ ϕ∗ (x∗ , u∗ )
β = k(0)
α = inf f (x)
(P)
ϕ(x, 0) = f (x) ∀ x ∈ X
h(u) = inf x ϕ(x, u)
α = h(0)
∗
54
∗
−β ≤ α
En el caso particular, cuando ϕ = ϕ∗∗ , entonces (Q) es también el dual de
(P ) y f ∗ = k.
Se nota por construcción que h∗ es convexa semicontinua inferiormente (sci)
y por consiguiente (Q) es siempre un problema de optimización convexa.
Si ϕ es convexa sobre R n × R p , entonces h es convexa sobre R p . Si h es
convexa y propia una condición necesaria y suficiente para que no exista
salto de dualidad es que h sea sci en 0 (en general ϕ sci no implica que h
sea sci).
Si h es convexa y sci en 0 y si además α = h(0) < +∞, entonces necesariamente h(0) = h∗∗ (0). En consecuencia no se tiene salto de dualidad.
Ahora, estamos interesados en las soluciones optimales de (P ) y (Q).
u∗ es solución optimal de (Q) ⇔ h∗ (u∗ ) ≤ h∗ (u∗ ) ∀u∗
m
u∗ ∈ ∂h∗∗ (0)
⇐⇒
0 ∈ ∂h∗ (u∗ )
Por consiguiente, el conjunto de soluciones optimales de (Q) es el subdiferencial de h∗∗ en 0. Si h∗∗ (0) = h(0), es decir si α = −β, es también el
subdiferencial de h en 0. Ası́, obtenemos el siguiente resultado:
Proposición 4.1.1 Supongamos que h es convexa y sci.
1. Si 0 ∈ ri(dom h), entonces α = −β y el problema dual admite al
menos una solución optimal.
2. Si 0 ∈ int(domh) entonces el conjunto de soluciones es compacto.
Supongamos ahora que ϕ es convexa, s.c.i y propia, entonces el esquema
es simétrico, f = k ∗ y ϕ∗∗ = ϕ. El conjunto de las soluciones optimales de
(P ) es el subdiferencial de k ∗ en 0. Ası́, existe el análogo de la proposición
4.1.1.
55
Supongamos que u∗ es solución optimal de (Q), que ϕ = ϕ∗∗ y que α = −β.
Examinemos las caracteristicas de las soluciones optimales de (P ).
x es solución optimal de (P ) ⇔ f (x) = α = −β = −h∗ (u∗ )
Por consiguiente
x es solución optimal de (P ) ⇔ f (x) + h∗ (u∗ ) = 0
m
ϕ(x, 0) + ϕ∗ (0, u∗ ) = hx, 0i + h0, u∗ i
m
(x, 0) ∈ ∂ϕ∗ (0, u∗ ) ⇔ (0, u∗ ) ∈ ∂ϕ(x, 0)
Por consiguiente las soluciones optimales de (P ) se deducen de la subdiferencial de ϕ∗ en (0, u∗ ) donde u∗ es solución optimal de (Q). Se tiene el
análogo por las soluciones optimales de (Q).
4.1.1
Noción del Lagrangiano
Definamos
L(x, u∗ ) = − sup[hu, u∗ i − ϕ(x, u)] = inf [ϕ(x, u) − hu, u∗ i]
u
u
Puesto que
h∗ (u∗ ) = ϕ∗ (0, u∗ ) = sup[hu, u∗ i − ϕ(x, u)]
x,u
Se tiene que
h∗ (u∗ ) = sup[−L(x, u∗ )] = − inf L(x, u∗ )
x
x
y como
β = inf
h∗ (u∗ )
∗
u
se tiene
−β = sup inf L(x, u∗ )
u∗
x
56
(4.1)
Por otro lado
sup L(x, u∗ ) = sup inf [ϕ(x, u) + h0 − u, u∗ i]
u∗
u∗
u
Para x fijo definamos
θx (u) = ϕ(x, u)
entonces se tiene
sup L(x, u∗ ) = θx∗∗ (0) ≤ θx (0) = ϕ(x, 0) = f (x)
u∗
por lo tanto
inf sup L(x, u∗ ) ≤ inf f (x) = α
x
x
u∗
Por consiguiente, si ϕ es convexa, s.c.i y propia, entonces θx es convexa,
s.c.i y θx (u) > −∞ ∀u. Se tiene también:
θx∗∗ (0) = θx (0) = ϕ(x, 0) = f (x)
(4.2)
y por consiguiente
inf sup L(x, u∗ ) = inf f (x) = α
x
x
u∗
ası́
−β = sup inf L(x, u∗ ) ≤ inf sup L(x, u∗ ) = α
u∗
x
x
u∗
Se nota que si ϕ es convexa entonces para todo u∗ ,
x → L(x, u∗ ) = inf [ϕ(x, u) − hu, u∗ i]
u
es convexa porque la aplicación (x, u) → ϕ(x, u) − hu, u∗ i es convexa; por
otro lado para x fijo, la aplicación u∗ → L(x, u∗ ) es cóncava, sci como
ı́nfimo de funciones afı́nes.
Recuerde que (x, u∗ ) es llamado punto silla de L si:
L(x, u∗ ) ≤ L(x, u∗ ) ≤ L(x, u∗ ) ∀x, ∀u∗
En tal caso se tiene:
inf sup L(x, u∗ ) ≤ sup L(x, u∗ ) = L(x, u∗ )
x
u∗
u∗
57
L(x, u∗ ) = inf L(x, u∗ ) ≤ sup inf L(x, u∗ )
x
u∗
x
Por otro lado, se tiene siempre que:
inf sup L(x, u∗ ) ≥ sup inf L(x, u∗ )
x
u∗
u∗
x
Por lo que se tiene la igualdad
inf sup L(x, u∗ ) = sup inf L(x, u∗ )
x
u∗
u∗
x
Teorema 4.1.1 Si ϕ = ϕ∗∗ , entonces (x, u∗ ) es punto silla del lagrangiano
si y solo si se tiene que x es solución optimal de (P ), u∗ es solución optimal
de (Q) y α = −β
Demostración. Se sabe por (2) que supu∗ L(x, u∗ ) = f (x) y por (1) que
inf x [L(x, u∗ )] = −h∗ (u∗ ). Por consiguiente (x, u∗ ) es punto silla si y solo
si f (x) + h∗ (u∗ ) = 0 o f (x) ≥ α, h∗ (u∗ ) ≥ β y α + β ≥ 0
Se tiene entonces: (x, u∗ ) es punto silla si y solo si
α+β =0
(no existe salto de dualidad)
f (x) = α
x es solución optimal de (P )
h∗ (u∗ ) = −β u∗ es solución optimal de (Q)
4.2
Dualidad en Programación Lineal
Sea
α = inf [ha, xi : Bx ≥ b]
x≥0
(P )
con la hipótesis siguiente
∃ x tal queBx ≥ b, x ≥ 0
que es equivalente a α < +∞.
Sea
(
ha, xi si Bx ≥ b, x ≥ 0,
f (x) =
+∞ en caso contrario.
58
(H0 )
(
ϕ(x, u) =
ha, xi si Bx ≥ b + u, x ≥ 0,
+∞ en caso contrario.
De esto se sigue que f y ϕ son funciones convexas, s.c.i, propias y f (x) =
ϕ(x, 0) ∀x
Sea h(u) = inf ϕ(x, u), entonces se tiene que α = h(0) y h convexa.
Por otro lado, se tiene
Sλ (ϕ) = {(x, u) : ha, xi ≤ λ, Bx − u ≥ 0, x ≥ 0}
y por lo tanto, Sλ (ϕ) es un poliedro convexo.
u ∈ Sλ (h) ⇐⇒ ∀µ > 0 ∃ x tal que ϕ(x, u) ≤ µ
Por lo tanto
Sλ (h) =
\
proju Sλ (ϕ)
µ>λ
como la proyección de un poliedro convexo sobre un subespacio es un
poliedro convexo entonces cerrado, se tiene que proju Sλ (ϕ) es cerrado ∀µ,
esto implica que Sλ (h) es cerrado ya que es intersección de cerrados, por
lo tanto h es s.c.i.
Por otro lado se sabe que h(0) = α < +∞. Por lo tanto debido a que h es
convexa y s.c.i se tiene h∗∗ = −β = α = h(0)
Calculemos ahora la conjugada de h
h∗ (u∗ ) = ϕ∗ (0, u∗ ) = sup[hu, u∗ i − ha, xi : Bx − u ≥ 0, x ≥ 0]
x,u
• Si u∗ tiene una componente < 0 digamos la componente i0 , tomando
x = x, ui = −(Bx−b)i ) si i 6= i0 , ui0 → −∞, entonces h∗ (u∗ ) = +∞.
• Si u∗ ≥ 0
h∗ (u∗ ) = supx≥0 [h−b + Bx, u∗ i − ha, xi] = h−b, u∗ i + suphx, B t u∗ − ai
x≥0
(
∗
∗
h (u ) =
h−b, u∗ i si B t u∗ − a ≤ 0,
+∞
en caso contrario.
59
Por lo tanto β = −α = inf[h−b, u∗ i : u∗ ≥ 0, B t u∗ ≤ a]
De esta manera
sup[hb, u∗ i : u∗ ≥ 0, B t u∗ ≤ a] = inf[ha, xi : x ≥ 0, Bx ≥ b].
4.3
Pertubación vertical con solo restricciones
de desigualdad
Sea el problema
α = inf[f (x) : gi (x) ≤ 0, i = 1, ..., p ]
Con las hipótesis siguientes:
• f , gi convexas, s.c.i y propias
(H0 )
• ∃ x tal que f (x) < +∞, gi (x) < 0 ∀i = 1, ..., p
• α > −∞
(H1 )
(H2 )
Observese que (H1 ) + (H2 ) → |α| < +∞
Definamos
(
fe(x) si gi (x) ≤ 0 ∀i
f (x) =
+∞ en caso contrario
(
f (x) si gi (x) + ui ≤ 0 ∀i
ϕ(x, u) =
+∞ en caso contrario
Se sigue que ϕ es convexa y s.c.i en razón de (H0 ) y (H1 ).
ϕ es propia en razón de (H0 ) y (H1 ), por consiguiente ϕ = ϕ∗∗ .
Por otro lado
h(u) = inf ϕ(x, u)
x
Es convexa, debido a que ϕ es convexa, además si se toma ui ≤ −gi (x) ∀i
se tiene h(u) ≤ f (x).
Dado
n
Y
V =
] − ∞, −gi (x)[ ⊂ dom(h)
i=1
60
Se tiene que V es una vecindad de 0, luego 0 ∈ int(dom(h)).
En consecuencia:
• h(0) = h∗∗ (0), no se tiene salto de desigualdad.
• ∂h(0) 6= ∅ y ∂h(0) es compacto, por consiguiente el problema dual
tiene un conjunto de soluciones optimales que se convexo, compacto
y no vacio.
−α = +β = inf
h∗ (u∗ )
∗
u
con
h∗ (u∗ ) = sup[hu, u∗ i − ϕ(x, u)]
x,u
∗
∗
h (u ) = sup[hu, u∗ i − f (x) : gi (x) + ui ≤ 0]
x,u
• Si u∗ tiene una componente menor que cero, digamos la componente
i0 , tomando x = x, ui = −gi (x) si i =
6 i0 , ui0 → −∞, entonces
∗ ∗
h (u ) = +∞.
• Si u∗ ≥ 0
h∗ (u∗ ) =
[−f (x) −
sup
X
u∗i gi (x)]
x∈[dom(f )∩(∩dom(gi ))]
Luego
−β = sup[−h∗ (u∗ )] = α
u∗
α = sup inf [f (x) +
X
u∗ ≥0 x
u∗i gi (x)] = sup inf L(x, u∗ )
u∗ ≥0 x
Esta es la dualidad lagrangiana. Sea u∗ solución optimal del problema dual,
entonces x es solución del problema primal si y solo si
X
X
f (x) +
u∗i gi (x) ≤ f (x) +
u∗i gi (x) ∀ x
(4.3)
y
f (x) +
X
u∗i gi (x) ≤ f (x) +
61
X
u∗i gi (x) ∀ u∗ ≥ 0
(4.4)
(4.4)
⇔ gi (x) ≤ 0 ∀i y u∗i gi (x) = 0 ∀i
En general 4.3 no es suficiente para obtener las soluciones del problema
primal.
Ejemplo.
α = inf[x : −x ≤ 0 ]
Aqui fe(x) = x y g(x) = −x
Cuya solución optimal es x = 0
El problema dual es
−α = inf
h∗ (u∗ )
∗
u
Donde
(
h∗ (u∗ ) = sup[−x + u∗ x] =
x
+∞ si u∗ 6= 1,
0
si u∗ = 1.
Luego la solución única del problema dual es u∗ = 1. El conjunto de
soluciones de (4.3) es R.
4.4
Perturbación Vertical - Caso General
Considerece el problema
α = inf[f (x) : gi (x) ≤ 0, i = 1, ..., p, Ax + a = 0]
Donde
[H1 ] f , gi son convexas, sci y propias sobre R n , A es una matriz q × n
de rango q, a ∈ R q
[H2 ] ∃ x
e ∈ intdom(f ) ∩ [∩pi=1 dom(gi )] tal que Ae
x + a = 0, gi (e
x) < 0
∀i = 1, ..., p
Se sigue de [H2 ] que α < +∞. Considere:
(
f (x) si gi (x) + ui ≤ 0, Ax + a + v = 0
ϕ(x, u, v) =
+∞ en caso contrario
62
h(u, v) = inf ϕ(x, u, v)
x
Entonces, α = h(0, 0). En razón de [H1 ] y [H2 ] ϕ es convexa, sci y propia,
ası́ h es convexa. Mostraremos que h es continua en (0, 0).
En razón de [H2 ] existe X ∈ V (e
x) tal que
f (x) ≤ f (e
x) + 1 < +∞ ∀x ∈ X
1
gi (e
x) < 0 ∀x ∈ X
2
Debido a que A es de rango maximal y Ae
x + a = 0, existe V ∈ V (0) en R p
tal que ∀v ∈ V , existe x ∈ X con Ax + a + v = 0.
∀i = 1, ..., p, gi (x) ≤
x) + ui ≤ 0 ∀ i.
Por otro lado existe U ∈ V (0) en R p tal que ∀u ∈ U , 21 gi (e
Se sigue que si (u, v) ∈ U × V entonces existe x ∈ X con Ax + a + v = 0,
gi (x) + ui ≤ 0 y f (x) ≤ f (e
x) + 1
Luego
h(u, v) = f (e
x) + 1 < +∞ ∀(u, v) ∈ U × V.
Por consiguiente (0, 0) ∈ int(dom(h)), h es continua en (0, 0) y α = −β. Si
α > −∞, el conjunto de soluciones optimales de (Q) es compacto no vacio.
h∗ (u∗ , v ∗ ) = sup [hu, u∗ i + hv, v ∗ i − f (x) : gi (x) + ui ≤ 0, Ax + a + v = 0]
u,v,x
• Si u∗i0 < 0, haciendo x = x
e, ui = 0 ∀i 6= i0 , vj = 0 ∀j y haciendo
variar ui0 en ] − ∞, −gi0 (e
x)], se obtiene que h∗ (u∗ , v ∗ ) = ∞
T Tp
• Si u∗ ≥ 0 poniendo D = dom(f ) ( i=1 dom(gi )), entonces
X
h∗ (u∗ , v ∗ ) = sup [−ha + Ax, v ∗ i −
u∗i gi (x) − f (x) ]
x∈D
y debido a que
β = −α = inf
h∗ (u∗ , v ∗ ) =
∗ ∗
u ,v
inf
u∗ ≥0,v ∗
h∗ (u∗ , v ∗ )
Se tiene
α=
sup
inf [ha + Ax, v ∗ i +
u∗ ≥0,v ∗ x∈D
63
X
u∗i gi (x) + f (x) ]
Es posible debilitar la hipótesis [H2 ] de la manera siguiente:
[H20 ] ∃ x
e ∈ ri(dom(f ))
p
\ \
x + a = 0, gi (e
x) < 0
( (dom(gi ))) : Ae
i=1
Se tiene entonces debido a [H20 ] que 0 ∈ ri(dom(h)). Nosotros probaremos
que [H20 ] implica que 0 ∈ int(dom(h)). Aqui α = −β y existen soluciones
optimales para el problema dual. Es suficiente demostrar que si (u, v) ∈
dom(h), entonces ∃ t > 0 tal que (−tu, −tv) ∈ dom(h).
Supongamos entonces que (u, v) ∈ dom(h), entonces ∃x ∈ dom(f ) tal que
Ax + vi + a = 0 y gi (x) + ui ≤ 0, esto implica que x ∈ dom(gi ).
T Tp
Recordemos que x
e ∈ ri(dom(f )) ( i=1 (dom(gi ))) entonces existe t > 0
tal que
x
e + t(e
x − x) ∈ ri(dom(f ))
p
\ \
( (dom(gi ))) ∀t ∈ [0, t]
i=1
Como los gi son continuas en [0, t] entonces debido a que gi (e
x) < 0, existe
e
e
e
t ∈ [0, t] tal que gi (e
x + t(e
x − x)) − tui ≤ 0 ∀i
Por otro lado A(e
x+e
t(e
x − x)) + a − e
tvi = 0 por lo tanto h(−e
tu, −e
tv) ≤
e
f (e
x + t(e
x − x)) < +∞.
4.5
Ejemplo de perturbaciones no Verticales
Considere el problema
α = infn [f (Ax) + g(Bx)]
x∈R
Donde
H1 ) A es una matriz de orden p × n, B es una matriz de orden q × n,
f : R p → R, g : R q → R; f , g son convexas, s.c.i y propias.
H2 ) ∃ x
e ∈ R n tal que Ae
x ∈ intdom(f ) y Be
x ∈ int(dom(g)).
64
Observe que H2 ) ⇒ α < +∞
Considere:
ϕ(x, u, v) = f (Ax + u) + g(Bx + v)
y
h(u, v) = inf ϕ(x, u, v)
x
Entonces ϕ es convexa, sci y propia, por lo tanto h es convexa y h(0, 0) = α.
Mostraremos que h es continua en (0, 0)
Ae
x ∈ int(dom(f )) ⇒ ∃U ∈ V (0) tal que u ∈ U ⇒ f (Ae
x +u) ≤ f (Ae
x)+1
Be
x ∈ int(dom(g)) ⇒ ∃V ∈ V (0) tal que v ∈ V ⇒ g(Be
x + v) ≤ g(Be
x) + 1
y por lo tanto
h(u, v) ≤ f (Ae
x) + g(Be
x) + 2 ∀ (u, v) ∈ U × V ∈ V (0, 0).
Por lo tanto h es continua en (0, 0) y α = −β. Si α > −∞, entonces
el problema dual admite soluciones optimales, ademas el conjunto de esas
soluciones es convexo y compacto.
h∗ (u∗ , v ∗ ) = sup [hu, u∗ i + hv, v ∗ i − f (Ax + u) − g(Bx + v)]
u,v,x
= sup [hAx+u, u∗ i−f (Ax+u)+hBx+v, v ∗ i−g(Bx+v)−hx, At u∗ +B t v ∗ i]
u,v,x
h∗ (u∗ , v ∗ ) = sup [hy, u∗ i − f (y) + hz, v ∗ i − g(z) − hx, At u∗ + B t v ∗ i]
x,y,z
(
∗
∗
∗
h (u , v ) =
[f ∗ (u∗ ) + g ∗ (v ∗ )] si At u∗ + B t v ∗ = 0
+∞
en caso contrario
y por consiguiente
−α = +β = inf
[f ∗ (u∗ ) + g ∗ (v ∗ ) : At u∗ + B t v ∗ = 0].
∗ ∗
u ,v
Aqui en este caso el Lagrangiano es:
l(x, u∗ , v ∗ ) = hx, At u∗ + B t v ∗ i − f ∗ (u∗ ) − g ∗ (v ∗ )
65
Si (u∗ , v ∗ ) es solución optimal del dual, entonces x es solución optimal del
primal si y solamente si
l(x, u∗ , v ∗ ) ≤ l(x, u∗ , v ∗ ) ≤ l(x, u∗ , v ∗ ) ∀x, u∗ v ∗
es decir, si Ax ∈ ∂f ∗ (u∗ ) y Bx ∈ ∂g ∗ (v ∗ ), porque AT u∗ + B T v ∗ = 0.
Casos Particulares: Si A = I, B = I, se obtiene:
α = infn [f (x) + g(x)] Problema primal
x∈R
β = inf
[f ∗ (x∗ ) + g ∗ (−x∗ )] Problema dual
∗
x
Observación:
Aun se puede reemplazar (H2 ) por
(H20 ) ∃e
x ∈ R n tal que Ae
x ∈ ri(dom(f )) y Be
x ∈ ri(dom(g))
Se tiene entonces que 0 ∈ ri(dom(h)), en consecuencia α + β = 0.
4.6
Inf convolución y el Sub diferencial de la
suma de dos funciones convexas
Sea f y g dos funciones convexas propias. Sea además A = epi(f ), B =
epi(g) y C = epi(f ) + epi(g), entonces C es convexa. Es facil de ver que
(x, λ) ∈ C y µ > λ ⇒ (x, µ) ∈ C
Definamos h(x) = inf[λ : (x, λ) ∈ C], debido a que C es convexo, se tiene
que h es convexa y C ⊂ epi(h) ⊂ C.
Observe que A, B cerrados no implica que C sea cerrado.
Se tiene también
h(x) = Inf [λ1 + λ2 : (x1 , λ1 ) ∈ A, (x2 , λ2 ) ∈ B],
o también
h(x) = Inf [f (x1 ) + g(x2 ) : x = x1 + x2 ]
66
Se escribe h = f ∇g
Facilmente se ve que: f ∇g = g∇f
h(x) = Infy [f (x − y) + g(y)]
h es convexa mas no necesariamente sci cuando f y g son sci.
Proposición 4.6.1 Sean f , g funciones convexas, propias y sci, entonces:
a) (f ∇g)∗ = f ∗ + g ∗
b) (f + g)∗ = f ∗ ∇g ∗
Demostración.
a) Pongamos h = f ∇g
h∗ (x∗ )
=
sup[hx, x∗ i − f (x − y) − g(y)]
=
sup[hx − y, x∗ i + hy, x∗ i − f (x − y) − g(y)]
x,y
x,y
= f ∗ (x∗ ) + g ∗ (x∗ )
b) Se deduce que
(f ∇g)∗∗ = (f ∗ + g ∗ )∗ = (f ∇g)
de donde se tiene b.
Nosotros usaremos este resultado para el calculo del subgradiente de la
suma. Antes consideraremos un resultado trivial.
Proposición 4.6.2 Sean f , g funciones convexas, propias, s = f + g
a ∈ dom(s) tal que ∂f (a) 6= ∅ y ∂g(a) 6= ∅, entonces:
∂s(a) ⊃ ∂f (a) + ∂g(a)
Demostración.
x∗ ∈ ∂f (a) ⇒ f (a) + hx∗ , x − ai ≤ f (x) ∀ x
67
x∗ ∈ ∂g(a) ⇒ g(a) + hy ∗ , x − ai ≤ g(x) ∀ x
por lo tanto
s(a) + hx∗ + y ∗ , x − ai ≤ s(x) ∀ x
y
x∗ + y ∗ ∈ ∂s(a)
Teorema 4.6.1 Sean f , g funciones convexas, sci y propias (Aqui s =
f + g es convexa, sci y propia). Supongamos que ∃ x
e ∈ ri(dom(f )) ∩
ri(dom(g)), entonces:
a) (f + g)∗ = f ∗ ∇g ∗
b) ∀a∗ ∈ f ∗ ∇g ∗ , ∃ x∗ , y ∗ tal que x∗ + y ∗ = a∗ y (f ∗ ∇g ∗ )(a∗ ) =
f ∗ (x∗ ) + g ∗ (y ∗ )
c) si ∂f (a) 6= ∅, ∂g(a) 6= ∅, entonces ∂f (a) + ∂g(a) = ∂s(a)
Demostración. Debido a que s = f + g, se tiene que s es convexa, s.c.i y
propia
−s∗ (a∗ ) = Inf [f (x) + g(x) − ha∗ , xi]
(D)
Debido a que s∗ es convexa, sci y propia, −s∗ (a∗ ) < +∞ ∀ a∗
Definamos:
ϕ(x, u) = f (x + u) + g(x) − ha∗ , xi
entonces ϕ es convexa, s.c.i, propia y ϕ∗∗ = ϕ
ϕ∗ (x∗ , u∗ ) = sup[hx, x∗ i + hu, u∗ i − f (x + u) − g(x) + ha∗ , xi]
= sup[hx + u, u∗ i − f (x + u) + hx, x∗ + a∗ − u∗ i − g(x)]
ϕ∗ (x∗ , u∗ ) = f ∗ (u∗ ) + g ∗ (x∗ + a∗ − u∗ )
68
Definamos h(u) = inf x ϕ(x, u), se va mostrar que 0 ∈ ri(dom(h))
Sea u ∈ dom(h) ⇒ ∃ x tal que x + u ∈ dom(f ), x ∈ dom(g)
Debido a que x
e ∈ ri(dom(f )) ∩ ri(dom(g)) ∃t > 0 tal que
x
e + t(e
x − x − u) ∈ dom(f )
x
e + t(e
x − x) ∈ dom(g)
se tiene entonces
h(−tu) ≤ f (e
x + t(e
x − x − u)) + g(e
x + t(e
x − x)) − ha∗ , x
e + t(e
x − x − u)i < +∞
Por consiguiente u ∈ dom(h) ⇒ ∃ t > 0 tal que −tu ∈ dom(h) y de
esta manera 0 ∈ ri(dom(h)). No hay salto de dualidad y el problema dual
admite soluciones cuando s∗ (a∗ ) es finita.
Por consiguiente +s∗ (a∗ ) = inf ϕ∗ (0, u∗ ).
s∗ (a∗ ) = inf[f ∗ (u∗ ) + g ∗ (a∗ − u∗ )] = (f ∗ ∇g ∗ )(a∗ )
C) a∗ ∈ ∂s(a) ⇒ s∗ (a∗ ) + s(a) = ha, a∗ i. Existen x∗ , y ∗ tal que
s∗ (a∗ ) = f ∗ (x∗ ) + g ∗ (y ∗ ) con x∗ + y ∗ = a∗ .
Por consiguiente
f ∗ (x∗ ) + f (a) + g ∗ (y ∗ ) + g(a) = hx∗ , ai + hy ∗ , ai
o
f ∗ (x∗ ) + f (a) ≥ ha, x∗ i
g ∗ (y ∗ ) + g(a) ≥ ha, y ∗ i
por consiguiente
f ∗ (x∗ ) + f (a) = ha, x∗ i ⇒ x∗ ∈ ∂f (a)
g ∗ (y ∗ ) + g(a) = ha, y ∗ i ⇒ y ∗ ∈ ∂g(a)
y
∂∇(a) ⊃ ∂f (a) + ∂g(a).
69
Contra ejemplo: Sean f, g : R → R definidos por:
(
1
x si x > 0
f (x) =
+∞
en caso contrario
y
(
g(x) =
− x1 si x < 0
+∞
en caso contrario
se tiene que f, g son convexas, sci y propias.
f ∇g(a) = 0 ∀ a
(
0
si x∗ = 0
∗ ∗
∗ ∗
f (x ) + g (x ) =
+∞ en otro caso
Aquı́ ri(dom(f ∗ )) ∩ ri(dom(g ∗ )) = ∅
4.7
Subdiferencial de una función máximo
de funciones
Sean fi , i = 1, ..., p, convexas, s.c.i y propias sobre R n . Considerese
Tp
h(x) = M axi=1,p fi (x) y supongase que dom(h) = i=1 dom(fi ) es no
vacio, entonces h es convexa, s.c.i y propia. Sea a ∈ dom(h). Calculemos
∂h(a). Se sabe que:
x∗ ∈ ∂h(a) ⇐⇒ hx∗ , x − ai + h(a) ≤ h(x)
o también
h(a) − hx∗ , ai ≤ h(x) − hx∗ , xi ∀ x
Por consiguiente x∗ ∈ ∂h(a) si y solo si a es solución optimal del problema
α = inf [h(x) − hx∗ , xi]
x
70
o también si a es solución optimal de
α = inf [t − hx∗ , xi : fi (x) − t ≤ 0]
x,t
(P )
Notemos que la condición de Slater tiene (haciendo t = 1 + h(a)) además
α > −∞ de donde ∂h(a) 6= ∅. Por consiguiente
x∗ ∈ ∂h(a) ⇐⇒ ∃ u∗ ≥ 0, u∗ ∈ R p
tal que (a, t = h(a), u∗ ) es punto silla del lagrangiano
X
l(x, t, u∗ ) = t − hx, x∗ i +
u∗i (fi (x) − t).
Se sigue que
(
∂h(a) =
)
P ∗
∗
X
u
≥
0,
u
=
1,
i
x∗ ∈ ∂(
u∗i fi (a)) :
.
u∗i (fi (a) − h(a)) = 0 ∀ i
Supongase que x
e∈
T
i=1,p
ri(dom(hi )) 6= ∅, entonces se tiene que
P ∗
u∗ ≥ 0,
ui = 1,
X
∂h(a) = x∗ ∈
u∗i x∗i : x∗i ∈ ∂fi (a)
u∗i (fi (a) − h(a)) = 0 ∀ i
71
.
Capı́tulo 5
Monótonia y continuidad
del subdiferencial
5.1
Nociones generales sobre las multiaplicaciones
Sean X e Y dos conjuntos, se dice que Γ es una multiaplicación de X en
Y , si a todo x ∈ X, Γ asocia un conjunto Γ(x) ⊂ Y . Se denotara por
→
Γ : X−
→Y .
La gráfica de Γ es el conjunto:
graph(Γ) = {(x, y) ∈ X × Y : y ∈ Γ(x)} ⊂ X × Y
Recı́procamente dada D ∈ X × Y podemos definir una multiaplicación Σ
a partir de D por Σ(x) = {y : (x, y) ∈ D}.
Se ve fácilmente que Γ(x) = {y : (x, y) ∈ graph(Γ)}.
Una multiaplicación entonces esta definida perfectamente por su gráfica.
De manera natural, definiremos Γ− la multiaplicación inversa de Γ por
Γ− (y) = {x : (x, y) ∈ graph(Γ)}. Entonces (Γ− )− = Γ.
72
Al contrario de las aplicaciones unı́vocas, cada multiaplicación tiene una
inversa. Por ejemplo:
→
Γ : R−
→R definida por Γ(x) = {x2 } ∀x,
(
√
√
{+ y, − y} si y ≤ 0
−
Γ (y) =
∅
si y < 0
Se llama dominio de Γ al conjunto
dom(Γ) = {x : Γ(x) 6= ∅}
Se ve entonces que
dom(Γ) = projX [graph(Γ)]
y
dom(Γ− ) = projY [graph(Γ)]
Sea f una función convexa, sci y propia sobre R n , entonces ∂f es una
multiaplicación de R n en R n . Por otro lado debido a que x∗ ∈ ∂f ⇔ x ∈
∂f ∗ (x∗ ). Se ve que ∂f ∗ es una multiaplicación inversa de ∂f .
5.2
Monotonı́a del subdiferencial
Si f es una función convexa diferenciable sobre un intervalo I de R, entonces
f 0 es creciente sobre I, es decir:
x1 < x2 ⇒ f 0 (x1 ) ≤ f 0 (x2 )
Se puede escribir entonces
(f 0 (x2 ) − f 0 (x1 ))(x2 − x1 ) ≥ 0 ∀x1 , x2 ∈ I
Generalicemos esto a una función convexa sobre R n .
Sea f una función convexa y propia sobre R n , x0 , x1 , ..., xp ∈ dom(∂f ) ⊂
dom(f ) y sea x∗i ∈ ∂(xi ) para i = 0, 1, ..., p se tiene entonces
73
hx∗0 , x1 − x0 i
hx∗1 , x2
− x1 i ≤ f (x2 ) − f (x1 ),
hx∗p−1 , xp − xp−1 i
hx∗p , x0
≤ f (x1 ) − f (x0 ),
− xp i
≤ f (xp ) − f (xp−1 ),
≤ f (x0 ) − f (xp ).
Poniendo xp+1 = x0 , se tiene al sumar:
p
X
hx∗i , xi+1 − xi i ≤ 0 ∀ x∗i ∈ ∂f (xi )
i=0
Se dirá que ∂f es una multiaplicación cı́clicamente monótona.
En particular se tiene
hx∗0 , x1 − x0 i + hx∗1 , x0 − x1 i ≤ 0
esto es:
hx∗1 − x∗0 , x1 − x0 i ≥ 0 ∀ x∗1 ∈ ∂f (x1 ), x∗0 ∈ ∂f (x0 )
que generaliza (f 0 (x2 ) − f 0 (x1 ))(x2 − x1 ) ≥ 0.
De manera que una función creciente sobre R sea la derivada de una función
convexa se tiene:
P
Si Γ es una multiaplicación maximal cı́clicamente monótona ( i.e. si
es
P
P
cı́clicamente monótona y graph( ) ⊃ graph(Γ), entonces Γ = ) entonces
existe f convexa, sci y propia tal que Γ = ∂f . Ver el libro de Rockafellar
(Convex Analysis) para la prueba.
5.3
Continuidad de una multiaplicación
→ , x ∈ X. Γ es llamado sci en x si ∀ Ω abierto de Y con
−
Sea Γ : X →Y
Ω ∩ Γ(x) 6= ∅
∃ V ∈ ϑ(x) tal que Ω ∩ Γ(x) 6= ∅ ∀ x ∈ V
74
Γ es llamado scs en x si ∀ Ω abierto de Y con Ω ⊃ Γ(x)
∃ V ∈ ϑ(x) tal que Ω ⊃ Γ(x) ∀ x ∈ V
Note que si Γ es una únivoca (ie. Γ es una función) y si x ∈ dom(f ) se
tiene
la funcion Γ es continua en x ssi la aplicación Γ es sci y scs en x.
Se dirá que Γ es scs sobre X si Γ es scs en todo x ∈ X y si Γ(x) es un
compacto en todo x. Se tiene entonces
→
Teorema 5.3.1 Sea Γ : X −
→Y scs sobre X. Si K es un compacto de X,
entonces Γ(K) es un compacto de Y con
Γ(K) = {y : ∃ x ∈ K e y ∈ Γ(x)}
Demostración. Sea {Wi }i∈I una familia de abiertos cubriendo Γ(K),
S
se va mostrar que existe J finito, J ⊂ I tal que j∈J Wj ⊃ Γ(K). Sea
S
x ∈ X, Γ(x) es un compacto ⊂ Γ(K) ⊂ j∈J Wj . Donde existe I(x) finito,
S
I(x) ⊂ I tal que Γ(x) ⊂ ( i∈I(x) Wi ) = W (x), donde W (x) es una unión
finita de abiertos, por lo tanto abierto, W (x) ⊃ Γ(x) y como Γ es s.c.s en
x, entonces ∃V (x) ∈ ϑ(x) tal que x0 ∈ V (x) ⇒ Γ(x0 ) ⊂ W (x) ahora como
S
S
x∈K V (x) ⊃ K entonces existen x1 , x2 , ...., xp tal que
i=1,2,..,p V (xi ) ⊃
K sea x ∈ K, ∃i ∈ {i = 1, 2, .., p} tal que x ∈ V (xi ) ⇒ Γ(x) ⊂ W (xi ) y por
S
S
S
lo tanto Γ(K) ⊂ i=1,...,p W (xi ) = i=1,...,p [ j∈I(xi ) Wj ] y en consecuencia Γ(K)es recubierto por un número finito de Wj .
Se dirá que la multiaplicación Γ es cerrado si su gráfica es cerrada.
→
Teorema 5.3.2 Sea Γ : X −
→Y X ⊂ R n , Y ⊂ R p
a) si Γ es scs en todo x y Γ(x) cerrado ∀x, entonces Γ es cerrado.
b) Si Y es compacto y Γ es cerrado, entonces Γ es scs.
Demostración.
75
a) Sea (x, y) ∈
/ graph(Γ) es decir y ∈
/ Γ(x) y debido a que es cerrado se
tiene que
∃ > 0 tal que Γ(x) ∩ B(y, ) = ∅
Por consiguiente Γ(x) ⊂ [B(y, )]c que es abierto. Luego como Γ es
scs en x, ∃V ∈ ϑ(x) tal que x ∈ V ⇒ Γ(x) ⊂ [B(y, )]c lo que implica
que
graph(Γ) ∩ [V × B(y, )] = ∅.
b) Note que {x} × Γ(x) = graph(Γ) ∩ {x} × Y por consiguiente Γ(x) es
cerrado ⊂ Y , Y es compacto, entonces Γ(x) es compacto. Si Γ no
es s.c.s en x, entonces ∃Ω abierto ⊃ Γ(x) tal que no existe V ∈ ϑ(x)
con x ∈ V ⇒ Γ(x) ⊂ Ω. Tomando Vn = B(x, n1 ), se tiene que
existe xn con kxn − xk < n1 y yn ∈ Γ(xn ) ⊂ Y tal que yn ∈
/ Ω.
Note que xn → x luego como Y es compacto se sigue que exists una
subsucesión {ynk } → y ∈ Y . Luego {ynk } ∈ Y ∩ Ωc por consiguiente
y ∈ Y ∩ Ωc ⇒ y ∈
/ Ω ⊃ Γ(x) Luego de (xnk , ynk ) ∈ graph(Γ) que es
cerrado y (xnk , ynk ) → (x, y), se tiene que (x, y) ∈ graph(Γ) y por
tanto y ∈ Γ(x) que es una contradicción con y ∈
/ Ω ⊃ Γ(x).
Teorema 5.3.3 Sea ϕ : X×Y → R sci y sea Γ(x) = {y ∈ Y : ϕ(x, y) ≤ 0},
entonces Γ es cerrado.
Demostración.
grph(Γ) = {(x, y) : ϕ(x, y) ≤ 0} es cerrado porque ϕ es sci
5.4
Continuidad del subgradiente
Teorema 5.4.1 Sea f convexa, sci y propia, entonces ∂f es scs sobre
int(domf ).
Demostración.
a) Se muestra fácilmente que ∂f es cerrada. Se sabe que
∂f (x) = {x∗ : f (x) + f ∗ (x∗ ) − hx, x∗ i ≤ 0}
76
Tomando ϕ(x∗ , x) = f (x) + f ∗ (x∗ ) − hx, x∗ i, ϕ es s.c.i.
b) Sea x ∈ int(dom(f )), entonces existe r > 0 tal que B(x, 2r) ⊂
int(dom(f )) f es continua sobre B(x, 2r) entonces existen m, M tal
que −∞ < m ≤ f (x) ≤ M < +∞ ∀ x tal que kx − xk ≤ 2r. Sea
x ∈ B(x, r) y x∗ ∈ ∂f (x) se tiene
hx∗ , y − xi ≤ f (y) − f (x) ∀ y ∈ B(x, 2r)
Por consiguiente
hx∗ , y − xi ≤ M − m ∀ y ∈ B(x, 2r)
∗
Si x∗ 6= 0, tomando y = x+r kxx∗ k se tiene entonces ky−xk ≤ kx−xk+
r ≤ 2r y por consiguiente y ∈ B(x, 2r) y rkx∗ k ≤ M − m. Se tiene
entonces kx∗ k ≤ M −m
∀ ∈ B(x, r), ∀ x∗ ∈ ∂f (x). Poniendo Y =
r
→
−
{x∗ : kx∗ k ≤ M −m
r } compacto y por consiguiente ∂f : B(x, r)→Y es
s.c.s sobre B(x, r).
Corolario 5.4.1 Sea f convexa y diferenciable sobre Ω abierta y convexa
da R n , entonces ∇f es continua sobre Ω.
Demostración. Aquı́ ∂f (x) = {∇f (x)} por consiguiente ∂f es unı́voca,
además por el teorema anterior ∂f es scs, en consecuencia continua, entonces ∇f es continua sobre Ω.
5.4.1
Aplicación a la sensibilidad
Consideremos el siguiente programa convexo:
α = inf [f (x) : gi (x) ≤ 0, i = 1, ..., p, Ax + a = 0 ]
x
(P )
Con las hipótesis siguientes:
1. f y gi son convexas, s.c.i y propias sobre R n . a ∈ R q , A es una matriz
q × n de rango q
77
2. ∃e
x ∈ R n tal que Ae
x + a = 0 y las funciones f y gi son finitas y
continuas en x
e, gi (e
x) < 0 para i = 1, ..., p
3. α > −∞
Nosotros sabemos del Capı́tulo 4 que
α=
sup inf [f (x) +
X
u∗ >0,v ∗ x
u∗i gi (x) + hAx + a, v ∗ i ],
(Q)
y el problema dual (Q) admite soluciones optimales. Se designa por S
el conjunto de soluciones optimales de (P ) y por T el conjunto de soluciones optimales de (Q). Se tiene entonces que T es compacto no vacı́o.
Consideremos ahora el problema perturbado
h(u, v) = inf [f (x) : gi (x) + ui ≤ 0, i = 1, ..., p, Ax + a + v = 0 ]. (Pu,v )
x
h es convexa y (0, 0) ∈ int(dom(h)). En consecuencia ∀ 0 > 0, ∃U0 ×
V0 ∈ ϑ(0, 0) tal que U0 × V0 ⊂ int(dom(h)) y |h(u, v) − α| < 0 ∀ (u, v) ∈
U0 × V0 . Por otro lado, h es continua en (u, v) ∈ U0 × V0 , por consiguiente
h(u, v) = h∗∗ (u, v) = sup [hu, u∗ i + hv, v ∗ i − h∗ (u∗ , v ∗ ) ]
u∗ ,v ∗
o
(
∗
∗
∗
−h (u , v ) =
inf x [f (x) +
P
u∗i gi (x) + hAx + a, v ∗ i ] si u∗ ≤ 0,
−∞
caso contrario
En consecuencia
h(u, v) =
sup inf [f (x) +
u∗ ≤0,v ∗ x
X
u∗i (gi (x) + ui ) + hAx + a + v, v ∗ i ],
que es el problema dual (Qu,v ). (u∗ , v ∗ ) es solución optimal de (Qu,v ) sii
(u∗ , v ∗ ) ∈ ∂h(u, v). Designemos por T (u, v) el conjunto de las soluciones
optimales de (Qu,v ) y sea 1 > 0 entonces
T + B((0, 0), 1 ) = {(u∗ + u∗ , v ∗ + v ∗ ) : k(u∗ , v ∗ )k < 1 , (u∗ , v ∗ ) ∈ T }
78
es un abierto conteniendo a T , debido a que ∂h es scs en el int(dom(h)) y
T = ∂h(0, 0), ∃ U1 × V1 ∈ ϑ(0, 0) tal que U1 × V1 ⊂ U0 × V0 y
T (u, v) ⊂ T + B((0, 0), 1 ) ∀ (u, v) ∈ U1 × V1 .
En consecuencia la multiaplicación T es scs at (0, 0).
Por último, notemos que
S(u, v) = {x : ϕ(x, u, v) − h(u, v) ≤ 0}
donde
(
ϕ(x, u, v) =
f (x)
+∞
si Ax + a + v = 0 y gi (x) + ui ≤ 0 ∀ i
en caso contrario
Luego ϕ es s.c.i., por otro lado h es continua sobre U1 × V1 , por consiguiente la aplicación (x, u, v) → ϕ(x, u, v) − h(u, v) es s.c.i y por lo tanto
la multiaplicación S es cerrada esto significa que si (un , vn ) → (0, 0) y
xn ∈ S(un , vn ) ∀n y xn → x, entonces x ∈ S(0, 0) = S.
Ahora, asumamos que S es compacto no vacı́o, se va mostrar que la
e ∈ ϑ(0), Ve ∈ ϑ(0)
multiaplicación S es scs en (0, 0). Se tiene que existe U
e
e
tal que (u, v) ∈ U × V ⇒ h(u, v) ≤ α + 1. Por consiguiente existe r > 0
e ⊃ [−r, r]p , Ve ⊃ [−r, r]q . Poniendo
tal que U
f (x) ≤ α + 1;
b
S= x:
gi (x) − r ≤ 0, i = 1, .., p;
−r ≤ (Ax + a)j ≤ r j = 1, ..., q
e , v ∈ Ve implica Sb ⊃ S(u, v) ∀u ∈ U
e , v ∈ Ve Se va
h(u, v) ≤ α + 1 ∀u ∈ U
b
mostrar que S es compacto.
Sb∞ = {x : f (x) ≤ α+1}∞
p
\\
\
[ {x : gi (x) ≤ r}∞ ] {x : |(Ax+a)j | ≤ r}∞
i=1
Se obtiene entonces de esto
\
\
Sb∞ = {x : f (x) ≤ α}∞ {x : gi (x) ≤ 0}∞ {x : Ax = a}∞ = (S)∞ .
Pero (S)∞ = {0}, Sb es compacto, S es cerrado y Sb ⊃ S(u, v) en una
vecindad de (0, 0). Entonces S es scs en (0, 0).
79
5.4.2
Propiedades genéricas de las funciones convexas
Teorema 5.4.2 Las funciones convexas son localmente Lipschitz en el interior de su dominio.
Demostración. Recordemos la prueba hecha para mostrar que ∂f es
s.c.s. Sea x ∈ int(dom(f )), r > 0 tal que B = B(x, 2r) ⊂ int(dom(f ))
M = sup[f (x), x ∈ B], m = inf x∈B [f (x)]. Nosotros tenemos que
∀x ∈ B(x, r) ∀ x∗ ∈ ∂f (x) se tiene kx∗ k ≤ k =
M −m
r
Sean x, y ∈ B(x, r) y sean x∗ ∈ ∂f (x) y y ∗ ∈ ∂f (y), entonces f (y) − f (x) ≤
hx∗ , y−xi ≤ kky−xk y f (x)−f (y) ≤ hy ∗ , x−yi ≤ kky−xk por consiguiente
|f (y) − f (x)| ≤ kky − xk ∀ x, y ∈ B(x, r)
Por consiguiente f es lipschitz sobre B(x, r).
Un resultado debido a Rademacher dice que las funciones localmente Lipschitz son diferenciables en casi todas partes. Se sigue que las funciones
convexas son diferenciables en casi todas partes. En el caso de las funciones convexas existe una prueba directa, mucho mas simple que el de
Rademacher. Antes, nosotros probaremos algunos resultados.
Proposición 5.4.1 Sean X, Y dos espacios topológicos, ϕ : X × Y → R
→
sci sobre X × Y , Γ : X −
→Y s.c.s sobre X con Γ(x) 6= ∅ ∀x ∈ X. Sea
υ(x) = sup[ϕ(x, y) : y ∈ Γ(x)], entonces υ es scs sobre X
Demostración. Sea x0 ∈ X y λ > υ(x0 ) entonces ∀ y ∈ Γ(x0 ) se tiene
ϕ(x0 , y) < λ en consecuencia existe Vy abierto en ϑ(x), Wy abierto en ϑ(y)
tal que (x0 , y 0 ) ∈ Vy × Wy ⇒ ϕ(x0 , y 0 ) < λ. Siendo Γ(x0 )compacto y
S
W ⊃ Γ(x0 ) se tiene que existe y1 , ..., yp ∈ Γ(x0 ) tal que Γ(x0 ) ⊂
Sy∈Γ(x0 ) y
Tp
W
como inyi poniendoV =
i=1,..,p
i=1 Wyi , se tiene que V es abierto S
p
tersección finita de abiertos, V ∈ ϑ(x0 ). Por otro lado W = i=1 Wyi
es abierto incluyendo a Γ(x0 ). Debido a que Γ es s.c.s entonces existe
T
U ∈ ϑ(x0 ) tal que x ∈ U ⇒ Γ(x) ⊂ W . Sea ahora x ∈ U V , entonces
Γ(x) ⊂ W . Sea y ∈ Γ(x) entonces ∃i ∈ {1, ..., p} tal que y ∈ Wi . Debido
80
T
a que x ∈ U V ⊂ Vi y y ∈ Wi se tiene ϕ(x, y) < λ esto es verdad para
todo y. En consecuencia υ(x) ≤ λ.
Proposición 5.4.2 Sea f una función convexa, s.c.s. y propia, h fijo,
entonces x → f 0 (x, h) es s.c.s sobre int(dom(f ))
Demostración. Se sabe que f 0 (x, h) = supx∗ [hx∗ , hi : x∗ ∈ ∂f (x)].
Utilice la proposición precedente.
Observación, f 0 (x, h) es s.c.s pero no s.c.i. Considere por ejemplo
f : R → R con f (x) = |x|, se tiene
(
1 si x ≥ 0
0
f (x, h) =
−1
si x < 0
Proposición 5.4.3 Sea f una función convexa, sci y propia, x ∈ dom(f )
entonces f es diferenciable en x si y solo si f admite las derivadas parciales
en el punto x.
∂f
Demostración. Asumamos que las derivadas parciales ∂x
= f 0 (x, ei ) =
i
−f 0 (x, −ei ) existen. La función t → f (x + tei ) es derivable, entonces existe
ti > 0 tal que x ± ti ei ∈ dom(f ). El conjunto co(x ± ti ei ) ⊂ dom(f ) es una
vecindad de x, en consecuencia x ∈ int(dom(f )) entonces ∂f (x) 6= ∅. Si
∂f (x) es un singleton, acabó; en caso contrario existen x∗ , y ∗ ∈ ∂f (x) con
x∗ 6= y ∗ (existe i tal que x∗i 6= yi∗ ). Supongamos que x∗i < yi∗ , entonces
f 0 (x, ei ) =
sup hz ∗ , ei i ≥ yi∗
z ∗ ∈∂f (x)
f 0 (x, −ei ) =
sup hz ∗ , −ei i ≥ −x∗i
z ∗ ∈∂f (x)
f 0 (x, ei ) + f 0 (x, −ei ) ≥ yi∗ − x∗i > 0
que es una contradicción.
Teorema 5.4.3 Una función convexa en R n es en casi todas partes diferenciable sobre el interior de su dominio.
81
Demostración. El caso particular para n = 1 es simple. En efecto, si
f es convexa sobre un interval I ⊂ R, entonces podemos dividir I en dos
subintervalos I− , I+ donde f es creciente en I+ y decreciente en I− . Se
sabe que las funciones monótonas de una variable real son en casi todas
partes diferenciables (ver cualquier libro de análisis real).
Supongamos que n > 1. Sea C = int(dom(f ))
∂f
Di =
(x) existen ∀i = 1, · · · , n
∂xi
Tn
D = i=1 . Entonces D = {x ∈ C : ∇f (x) existe }.
D es medible. En efecto
Di = {x ∈ C : f 0 (x, ei ) + f 0 (x, −ei ) = 0}
La aplicación x → f 0 (x, ei ) + f 0 (x, −ei ) es scs, entonces es medible y por
lo tanto Di es también medible. Ası́ D es medible.
Sn
med(Dc ) = 0. En efecto, Dc = i=1 . Es suficiente mostrar que med(Dic ) =
0. Probemos para i = n. Es suficiente probar que es cierto para los
siguientes conjuntos:
Y
P =
[x̄i , x̄i + ] ⊂ C
vamos a mostrar que med(P ∩ Dnc ) = 0. En efecto, sea x = (y, xn ) con
R
Qn−1
y =h (x1 , · · · , xn−1 ), P̃i = i=1 [x̄i , x̄i + ], med(Dnc ∩ P ) = P 1Dnc (x)dx =
R R x̄n +
1Dnc (x)dxn dx1 · · · dxn . Esta ultima igualdad es posible usando
P̃
x̄n
R x̄ +
el Teorema de Fubini. Fijando y, x̄nn 1Dnc (x)dxn es la medida del conjunto D(y) = {xn ∈ R : (y, xn ) ∈ Dn }. Por definición, D(y) es el conjunto
de puntos donde la aplicación convexa t → f (y, x̄n + t) es derivable. Luego,
R x̄ +
el complemento es de medida cero, entonces x̄nn 1Dnc (x)dxn = 0. Finalmente med(P ∩ Dnc ) = 0.
Teorema 5.4.4 Sea f una función convexa sci y propia, x ∈ (dom(f )) y
= = {x : ∇f (x) existe } entonces ∂f (x) = co(S) con S = {e : ∃{xn } ⊂
= tal que xn → x y ∇f (xn ) → e}
82
Demostración.
a) co(S) ⊂ ∂f (x)
Debido a que ∂f (x) es convexo y cerrado es suficiente mostrar que
S ⊂ ∂f (x). Sea e ∈ S. Si e ∈
/ ∂f (x) entonces existe > 0 tal
que e ∈
/ ∂f (x) + B(0, ) abierto conteniendo a ∂f (x). ∂f scs en x
entonces ∃U ∈ ϑ(x) tal que x ∈ U entonces ∂f (x) ⊂ ∂f (x) + B(0, 3 ).
Si xn → x y ∇f (xn ) → e para n suficientemente grande xn ∈ U y en
consecuencia ∇f (xn ) ∈ ∂f (x) + B(0, 3 ) es decir k∇f (xn ) − ek ≤ 3
lo cual es contradictorio.
b) ∂f (x) ⊂ co(S)
Supongamos que x∗ ∈ ∂f (x) y x∗ ∈
/ co(S). Por el teorema de separación fuerte, existe d 6= 0 y α > 0 tal que kdk = 1 y
hl, di + α ≤ hx∗ , di ∀ l ∈ co(S)
En consecuencia
hl, di + α ≤ hx∗ , di ≤ f 0 (x, d) ∀ l ∈ S.
Sea la función convexa de una variable real θ(t) = f (x + td). Sea
n ∈ N, existe tn ∈]0, n1 [ tal que x+tn d ∈ int(dom(f )) y θ es derivable
en tn y θ0 (tn ) ≥ θ0 (0) ≥ hx∗ , di. Ahora, sea la multiaplicación Γ(x) =
{hx∗ , di : d ∈ ∂f (x)}, porque ∂f es scs en int(dom(f )), ası́ Γ es scs.
Se observa que Γ(x + tn d) = {θ0 (tn )}.
Puesto que Γ es scs en x̄ + tn d, entonces existe U ∈ ϑ(x̄ + tn d) tal
α
α
, θ0 (tn ) + 10
.
que x ∈ U , entonces Γ(x) ⊂ θ0 (tn ) − 10
Puesto que f es diferenciable en casi todas partes, entonces existe
{xn } ⊂ U tal que kxn − (x̄ + tn d)k ≤ n1 y ∇f (xn ) existe. Luego,
α
kxn − x̄k ≤ n1 + ktn dk ≤ n2 con xn → x y h∇f (xn ), di ≥ θ0 (tn ) − 10
≥
α
∗
hx , di − 10 .
Como f es localmente Lipschitz, entonces ∇f (x) es acotado en una
vecindad de x̄, en consecuencia existe una subsucesión {xnk } y ˜l tal
α
lo
que ˜l = lim ∇f (xnk ). Luego, ˜l ∈ S, es decir h˜l, di ≥ hx∗ , di − 10
cual es una contradicción.
83
5.5
-subdiferenciales
Sea f una función convexa propia, x ∈ dom(f ) y > 0. Se dice que x∗ es
un -subdiferencial de f en x si y solo si
f (x) + f ∗ (x∗ ) ≤ hx, x∗ i + Denotaremos por ∂ f (x) al conjunto de subdiferenciales de f en x.
Es fácil verificar que ∂ f (x) es un conjunto convexo y cerrado. En efecto,
la aplicación x∗ → f ∗ (x∗ ) − hx, x∗ i es convexa y sci y:
∂ f (x) = {x∗ : f ∗ (x∗ ) − hx, x∗ i ≤ − f (x)}
Otra propiedad de los - subdiferenciales es: Dados 0 < 1 < 2 , entonces ∂1 f (x) ⊂ ∂2 f (x). Esto implica que:
\
∂ f (x) = ∂f (x)
>0
∗
∗
Si reemplazamos f (x ) por su valor, obtendremos una definición equivalente para los -subdiferenciales, es decir:
x∗ ∈ ∂ f (x) si y solo si f (y) ≥ f (x) + hx∗ , y − xi − ∀y
Teorema 5.5.1 Si ∂f (x) es compacto y no vacı́o, entonces ∂ f (x) también
es compacto y no vacı́o ∀ > 0.
Demostración. Sabemos que ∂ f (x) = {x∗ : f ∗ (x∗ ) + f (x) − hx, x∗ i ≤ }.
Consideremos g : X ∗ → R definida por g(x∗ ) := f ∗ (x∗ ) + f (x) − hx, x∗ i.
Luego g es convexa sci y ∂ f (x) = S (g). Por hipótesis [S0 (g)]∞ = {0},
entonces [S (g)]∞ = {0}.
Teorema 5.5.2 Si f es convexa sci y propia, entonces ∂ f (x) 6= ∅ ∀x ∈
dom(f ) y ∀ > 0.
Demostración. Es consecuencia inmediata de la definición de supremo y
el hecho que:
f (x) = sup [hx, x∗ i − f ∗ (x∗ )]
x∗ ∈X ∗
84
Anuncio
Documentos relacionados
Descargar
Anuncio
Añadir este documento a la recogida (s)
Puede agregar este documento a su colección de estudio (s)
Iniciar sesión Disponible sólo para usuarios autorizadosAñadir a este documento guardado
Puede agregar este documento a su lista guardada
Iniciar sesión Disponible sólo para usuarios autorizados