DESPEJE DE VARIABLES

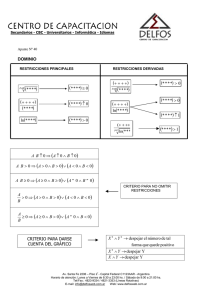
ACADEMIAS
ÁLGEBRA
DESPEJE DE VARIABLES
POII1XN1
DESARROLLO DEL TEMA
Definición
•
Despejar una variable en una fórmula es aislarla en un
miembro y expresarla en función de las variables restantes.
Transformar una fórmula es realizar las operaciones
necesarias para despejar una de las variables.
Para despejar una variable, se deberá analizar la expresión
y los términos que contengan a la incógnita se deberán
reunir en un solo miembro, para lograr esto se tienen que
realizar transposiciones de términos y las operaciones a
realizar serán inversas, es decir:
• Si una variable en un miembro se encuentra en forma
de suma, pasará al otro miembro en forma de resta.
• Si una variable en un miembro se encuentra en forma
de resta, pasará al otro miembro en forma de suma.
• Si una variable en un miembro se encuentra en forma
de multiplicación, pasará al otro miembro en forma de
división.
• Si una variable en un miembro se encuentra en forma
de división, pasará al otro miembro en forma de
multiplicación.
Si la variable a despejar esta elevada a la enésima
potencia, para despejarla se deberá extraer raíz
enésima a los dos miembros.
Clasificaremos lo anteriormente expuesto con el siguiente
ejemplo.
Si, a = 4v + h despejar "z"
5z + t
•
(5z + t) será llevado al primer miembro:
⇒ a(5z + t) = 4v + h
•
Efectuando en el primer miembro:
⇒ 5az + at = 4v + h
•
"at" será llevado al segundo miembro:
⇒ 5az = 4v + h – at
•
Despejando "z":
⇒z=
4v + h – at
5a
EJERCICIOS DE CLASE
Nivel I
1. Despejar "P".
A. q/t
B. t/q
2. Despejar "Q".
A. y + P
B.
2
x
y+P
A.
B. abc
P = q
q
t
4. Despejar "B".
A. 3A –5m
3
A
–5m
B.
3
C. qt
D. q2/t
yQ = QP + X2
2
C. x
y–P
2
D. x
P–y
C.
abc
bc + 1
D.
bc
a–1
3(A + B) = 5m
C. 5m – 3A
3
5m
–3
D.
B
5. Despejar la variable "K".
k =a
k+b
A. ab
C. a – 1
1–a
ab
ab
a
B. –
D.
a–b
(a – 1)b
3. Despejar "d".
abc – bcd = d
PRIMERA OPCIÓN NIVELACIÓN 2015-II
abc
bc – 1
1
ÁLGEBRA | N1
ACADEMIAS
DESPEJE DE VARIABLES
6. Despejar "q".
A. s + a
s+µ
B. s – a
s+µ
B. x =
A. u = v
2y
2
B. u = v
2y2
7. Despeje "x".
T = 2x g
L
A. T L
2 g
C. T g
2 L
B. 2T L
g
D.
A. c – a
T g
L
B. c – a
z
d2
2
D. Fd
m
B. q + p
q–p
10. En la ecuación despejar el valor de "A2".
A
D=
B.
BD2
1 – D2
C.
D.
B2D2
1 – D2
B. x = y + b
C. B = 2A – hd
h
2A
+ hd
D. B =
h
12. Despeja F en función de A, E y G; en: A = EG – F2.
A. F = A2 – EG
C. F = ± EG – A2
B. F = ± EG – A
D. F = EG –F
2
1
c–a
z
D.
c–a
C.
D. pq(q – p)
q+p
D. x = ± y + b
A. (m + n) .m
n
C. m – n
m+n
B. m + n
m–n
D. my + 1
y–m
20. Despeja b en: S = a + b n.
2
2
A.
13. Despeja x en términos de y:
x2
y= 2
x –1
PRIMERA OPCIÓN NIVELACIÓN 2015-II
.
19. Despeja "λ" en la expresión:
m+n+ n+1 = λ +2
m
n
n
11. En la siguiente expresión A = 1 h(B + d), despeja a B.
2
A. B = 2A – h
h
A
–
hd
B. B =
h
D. u = v
2y
2 u
18. Despeja x en términos de y ∧ b, en:
ay = ax2 + ab
A. x = y – b
C. x = ± y – b
A2 + B2
1 – D2
2
C. u = 3
4y2
v
17. Despeja "r", en: 1 – 1 = p + q
p q
r
p
+
q
A.
C. pq(q + p)
q–p
p–q
Q = mC(Tf – Ti)
i dé como respuesta el numerador.
A. Tf – Q
C. mCTf – Q
B. Tf – mCQ
D. 1 – Q
A.
y
y+1
Nivel III
9. Despejar "Ti".
B2D
D2 –1
D. x = ±
16. Despeja A, en: A – B = P
A+B
B(1
+
P)
A.
C. 1 + P
1–P
1–P
1
+
P
PB
B.
D.
P+B
B(1 – P)
kQ1Q2
2
Si se sabe que: d = m.
k
2
2
A. Fd
C. Fd m
k
kQ2
BD
y
y+1
15. Despeje "W", en: aw = cw – z.
8. Encontrar el valor de "Q1" de la siguiente ecuación:
B. Fm
Q2
y
y–1
C. x =
14. Despeja "u" en término de y ∧ v; en: y =
Nivel II
F=
y
y–1
A. x = ±
S = µq – a
q–1
C. s + a
s–µ
D. s – a
s–µ
s–a
n
B. 2s – an
n
2
C. 2s – n
n
s
–
an
D.
2
ÁLGEBRA | N1