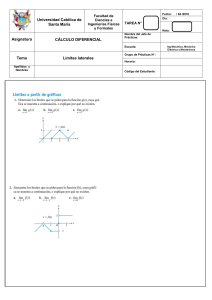
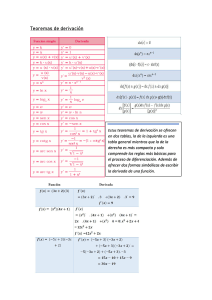
NIVELACIÓN DECARRERA FACULTAD DE CIENCIAS ADMINISTRATIVAS MATEMÁTICA Contenid o › Definición, propiedades, y determinación de un límite. › Limites laterales y continuidad. › La Derivada: Definición e interpretación geométrica. › Técnicas de Derivación. › La derivada como una razón de cambio (Función de Costo total, marginal; Función ingreso total, ingreso marginal › Reglas del producto y del cociente. UNIDAD 4 Introducción al cálculo Límites Los límites son una el corazón del cálculo, entre las principales aplicaciones del cálculo es el trazado de curvas, la optimización de funciones, el análisis de las tasas de cambio y el cálculo de áreas y de probabilidades, lo que distingue al cálculo del álgebra es el concepto del límite. El proceso del límite consiste en examinar el comportamiento de una función f(x) cuando “x” se aproxima a un número “c”, que puedo o no estar en el dominio de f. Para entender mejor el concepto de limites consideremos el siguiente ejemplo: Un gerente determina que cuando esta utilizando “x” porcentaje de la capacidad productiva de la planta de su compañía el costo total es: Límites En cientos de miles de dólares. La compañía tiene una política de rotar el mantenimiento de tal forma que nunca se utilice más del 80% de su capacidad. ¿Qué costo esperaría el gerente cuando la planta está operando a toda su capacidad permitida?. Parece evidente evaluar C(80) pero, al intentar realizar esa evaluación se obtiene una fracción de 0/0. sin embargo, aún se puede evaluar C(x) para valores de x que tienden a 80 por la izquierda x<80 y por la derecha x>80 Los valores de C(x) sugieren que tiende al número 7 a medida que x se acerca más y más a 80, siendo razonable que el gerente espere un costo de $700.000 cuando se utiliza el 80% de la capacidad de la planta Definición límite: Si f(x) se acerca más y más al número L cuando x se aproxima cada vez más a c, por ambos lados, entonces L es el límite de f(x) cuando x tiende a c. Ejemplo: Utilice una tabla de valores para calcular el límite Propiedades de límites: Ejemplos: Indeterminaciones: Levantar indeterminaciones Limites laterales Un limite existe si y solo si por la derecha y la izquierda dan el mismo resultado Indeterminación 0 / 0 Indeterminación 0 / 0 Ejemplo Ejemplos Ejemplo Tarea 52.1 Tarea 52.2 Continuidad Derivación Derivar mediante la definición Ejercicio en clase Reglas derivación Tarea 53 Razón de cambio Razón de cambio Aplicaciones de razones de cambio