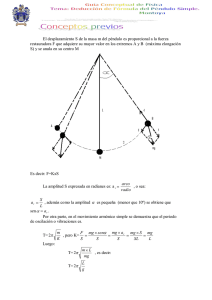
Grupo. “ L “ Univ. Henry Loza Choquetarqui Universidad Mayor de San Andrés Facultad de Ingeniería Curso Básico Laboratorio de Física Básica I FIS-100L 2/2014 INFORME Nº 9 “Pendulo simple” Docente: Auxiliar: Ing. Roberto Parra Zeballos Univ. Alex Gustavo GutierrezCoquendo Estudiante: Univ. Henry German Loza Choquetarqui Carrera: Ingeniería Petrolera Grupo: Fecha de Entrega: “L” 27 de noviembre , 2014 La Paz-Bolivia -1- Grupo. “ L “ Univ. Henry Loza Choquetarqui LAB. FISICA I U.M.S.A Facultad de Ingeniería INFORME N° 8 PENDULO SIMPLE I. OBJETIVOS.- Determinar experimentalmente el valor de la aceleración de la gravedad y determinar la ecuación empírica de la oscilación del péndulo. II. FUNDAMENTO TEORICO.- El péndulo simple consiste en una masa de dimensiones pequeñas suspendido de un hilo inextensible carente de peso. Cuando La masa es apartada de su posición de equilibrio y luego abandona, el péndulo oscila alrededor de esta posición en un plano vertical con movimiento que a la vez es periódico. El péndulo oscila con un periodo “T” que viene a ser el tiempo empleado en efectuar una oscilación completa. Se define la frecuencia “f” como el número de oscilaciones en una unidad de tiempo, por lo tanto la frecuencia es la inversa del periodo. 1 f (1) T P Para iniciar el análisis elegiremos dos ejes, uno en dirección tangente a la trayectoria y el otro en dirección radial. En el plano así formado se representaran todas las fuerzas que actúan sobre la masa del péndulo en el instante que es apartado de su posición de equilibrio de un pequeño ángulo “ ”. L T Si descomponemos el peso en la dirección del eje tangente a la trayectoria tenemos: Wy Wx Wx mgSin (2) Por lo tanto el ángulo en muy pequeño: W Fig. 1 La fuerza recuperadora será: Sin F Wx F mg (3) (4) -2- Grupo. “ L “ Univ. Henry Loza Choquetarqui El signo negativo indica que esta fuerza tiende a regresar al péndulo a su posición inicial. Como el ángulo “ ” es muy pequeño, se asume que el arco que describe la masa al oscilar es aproximadamente un desplazamiento lineal: X L Por lo tanto tenemos: F mgx L Donde se puede observar que la Fuerza recuperadora”F” para pequeños desplazamientos es directamente proporcional a la elongación “x”. F Kx mg , la denominada constante recuperadora del péndulo. L La condición necesaria para que el movimiento de un cuerpo sea catalogado como moviendo armónico simple (M. A. S.) es que se halle sometiendo a una fuerza recuperadora que sea directamente proporcional a la elongación y de sentido opuesto. En nuestro caso el moviendo analizado cumple con estas condiciones. Siendo que K Si Aplicamos la segunda Ley de Newton a la masa del péndulo tenemos. mg ma (8) a L (9) d 2 dt 2 (10) a Remplazando en la ecuación (8) d 2 g 0 dt 2 L (11) Se obtiene la ecuación característica del movimiento armónico Simple. El segundo de la ecuación representa la frecuencia angular “w” elevada al cuadrado, es decir. d 2 2 0 2 dt Como: 2 (12) g L 2 T (13) -3- Grupo. “ L “ Univ. Henry Loza Choquetarqui L g (14) 4 2 L T2 (15) T 2 g La ecuación (15) nos permite determinar la aceleración de la gravedad local previamente conocidos el periodo y la longitud del péndulo. Como es posible experimental con el péndulo simple, que no es nada mas que un modelo ideal y como el desarrollo a) Máximo ángulo de separación ( ): Antes de iniciar la practica es necesario determinar cuan pequeño puede ser considerado el ángulo se separación. Si la amplitud de oscilación no es pequeña. El periodo del péndulo esta en función del ángulo de separación según la siguiente expresión: T 2 L 1 14 sin 2 9 sin 2 ................) g 2 64 2 (16) Si depreciamos los términos de potencia superiores por ser valores muy pequeños y consideremos únicamente los dos primeros términos, tenemos: T 2 L 1 1 4 sin 2 g 2 (17) Si se desarrolla la serie sin 2 2 y se desprecian los términos superiores: T 2 2 L 1 ................) g 16 (18) Despejando de la ecuación (18) la aceleración de la gravedad además desprecian los términos superiores se tiene. g1 4 2 L 2 1 8 T 2 (19) Además: g 4 2 L T2 -4- Grupo. “ L “ Univ. Henry Loza Choquetarqui El error cometido en la determinación de la Aceleración de la gravedad por la influencia del ángulo de separación será: g g1 g g 2 8 g 2 g 8 (20) Para que este error relativo sea despreciable es necesario el valor 8 sea muy pequeño comparado con el error relativo prefijado para la determinación de la aceleración de la gravedad. Para cumplir esta condición se sugiere que sea por lo menos la décima parte del error relativo prefijado. 2 2 8 Er g (21) 10 Con la ecuación (21) podemos calcular el máximo valor que puede adoptar el ángulo de reparación en radianes: b) Máximo radio de la esfera: Como el péndulo que se utiliza en el experimento es en realidad un péndulo real, su movimiento también puede ser analizado mediante la dinámica del cuerpo rígido. P El periodo de oscilación del péndulo físico, es decir el péndulo real esta dado por: IP (22) mgL I P Momento de inercia respecto al eje de suspensión “p”. T 2 L Según el teorema de Steiner. R R R I P I O mL2 (23) I o Momento de inercia respecto al eje que pasa por el centro de gravedad de la esfera. Fig. 2 Io 2 mR 2 5 (24) -5- Grupo. “ L “ Univ. Henry Loza Choquetarqui Remplazando en la ecuación (22) se tiene: 2 R2 L 2 1 5 L T 2 g (25) Despejando la aceleración de la gravedad: 2 R2 4 2 2 1 5 L g2 T2 (26) El error que se comete en la medida de la aceleración de la gravedad al considerar se la masa de la esfera como la masa puntual será: 2 R2 g g 2 g g 2 5 L g 2 R 2 g 5 L2 (27) 2 R 2 Er g 2 5 L 10 (28) Utilizando la igualdad se puede calcular el radio máximo que debería tener la esfera para que el péndulo en estudio sea considerado péndulo simple: c) Medidas del periodo: Para no sobre pasar el error relativo prefijado en la determinación de la aceleración de la gravedad, se deben efectuar un numero mínimo se oscilaciones para la medida del periodo. El valor medido del periodo se lo puede expresar como: T T T Donde: T El valor mas probable del periodo T Error del periodo T tn n -6- Grupo. “ L “ Univ. Henry Loza Choquetarqui También en este caso: e n n Numero de oscilaciones. e Error del cronometrista (e = 0.2 segundos) T Donde: El error relativo del periodo será. E rT T e T Tn Despejando el número de oscilaciones: n III. e E rT T (29) Metodologia Experimental.- En este laboratorio péndulo simple mi grupo trabajo con todos los datos exactos para que asi al finalizar nuestros datos coinsidieran con la teoría mencionada IV. PROCEDIMIENTO.- A) Determinación de la aceleración de la gravedad: a) El Docente asignara el error porcentual prefijado para la determinación de la aceleración de la gravedad. b) Medir el diámetro de la esfera y la longitud del hilo (aproximadamente 90[cm.] del eje suspensión “p” al centro de gravedad de la esfera). c) Utilizando la ecuación (21), calcular la amplitud máxima “ ” y le desplazamiento lineal”x”. X L d) Mediante la ecuación (28) determinar el radio máximo y compararlo con el radio de la esfera para verificar si el péndulo en estudio puede ser considerado péndulo simple. e) Empleando la ecuación (15), realizar el proceso inverso de la propagación inversa de errores y determinar el error relativo que se debe cometer en la medida del periodo. f) Para 10 oscilaciones medir el periodo aproximado “T”, repetir el procedimiento tres veces y sacar el promedio. -7- Grupo. “ L “ Univ. Henry Loza Choquetarqui T t10 10 g) Con la ecuación (29), calcular el valor de “n”. h) Medir el tiempo para las “n” oscilaciones cinco veces, sacar el promedio y determinar el periodo y su correspondiente error B) Ecuación empírica del periodo: a) Considerando el numero “n” de oscilaciones determinado, medir el período de oscilaciones para diferentes longitudes del hilo. b) Construir una tabla de los valores de: T L V. Tratamiento de Datos.- A) Determinación de la aceleración de la gravedad: Con los valores obtenidos calcular la aceleración de la gravedad utilizando las ecuaciones (15), (19) y (26). DETERMINACION DE LA AMPLITUD MAXIMA Y DEL NUMERO DE OSILACIONES Error relativo de la gravedad (asignado) Amplitud angular Maxima =1.8 Longitud del Pendulo L1 L(cm) =0.01 L2 89,9 L3 90,1 L4 90,1 L5 90,5 90,1 90,1 SL=0.14 =0.174 =1.93* t10(segundos) 18,9 t 1,89 n(calculado) 33 DETERMINACION DE LA ACELERACION DE LA GRAVEDAD Masa del péndulo: m=45.2g Diametro de la esfera D=2.22cm = 965.51 =1.28 tn1(s) tn2(s) tn3(s) tn4(s) tn5(s) tn(s) -8- Grupo. “ L “ Univ. Henry Loza Choquetarqui 63,22 L(cm) tn(s) 63,27 90 63,3 g 4 2 L T2 g 63,01 80 60,34 4 2 90cm 1.89s 2 70 55,63 63,5 60 51,92 63,72 63,34 50 48,62 40 45,85 g 995.77cm / s 2 VALIDACION DE LA ECUACION DEL PENDULO a) Construir la grafica T versus L , ajustar la recta por el metido de mínimos cuadrados y obtener la pendiente “B”. 1 T B L2 -9- Grupo. “ L “ Univ. Henry Loza Choquetarqui Si linealizamos la anterior ecuación: Y LogC n Logx Yi A Bx i ; Donde: n = pendiente de la recta Ci = intersección con la ordenada A = LogC = 30.96 n=B= 0.359 La ecuación final es: y = 30.96+0.359 xi VI. CUESTIONARIO.1. Un alumno que ha realizado la practica del péndulo simple escribe el siguiente párrafo es su cuaderno de laboratorio “El objetivo fundamental de la practica del péndulo simple es observar como varia el valor de la gravedad en el laboratorio .Para ello se construyen diversos péndulos todos ellos con la misma masa y diversas longitudes ¿Son correctas las dos afirmaciones? R.-no es correcto xq con cualquier massa y diversas longitudes el valor de la gravedad no varia 2.-Aldeterminar “g” con un péndulo simple observamos que podemos actuarsobre dos parámetros : lalogitud del hilo y l amasa que depende de el ¿Cómo afectanal teriodo de osilacion del penduloestos dos parámetros? R.- afectan mucho por que no es lo mismop hascer osilar una esfera de masa m con una longitud L que hacerlo osilar a una longitud L1. 3.-Para un péndulo en osilacion señale los puntos en los cuales la velocidad Aceleracion y tencion en la cuerda alcanzan valores máximos Expleque mediante un dibujo L 4.-Con referencia a la pregunta anterior y con los datos del experimento calcule dichos valores máximos R.-978cm/s2 - 10 - Grupo. “ L “ Univ. Henry Loza Choquetarqui 5.-¿Por qué no es conveniente medir directamente el periodo midiendo el tiempo de una osilacion en vez de medirel tiempo de 10 osilaciones R.- por la variación de la velocidad en cierto tiempo a causa de la gravedad 6.-Para un péndulo en osilacion bosqueje los graficos de c vs t vs t y a vs t 7.-Calculese el periodo de un péndulo con L=1.000m a nivel del mar en l a paz y en la luna R.- por internet El periodo en la luna es T=0.56 para 10 osilaciones 8.-El peridodo de un péndulo simple de longidud L es T se esta longitud se reduce a la midad El nuevo periodo T se habrá reducido también a la mitad ¿Aumentara al doble ¿ Explique su respuesta. R.-reduce por ma mitad y un poco mas demostrado con los datos de el experimento 9.-Dos péndulos tienen distancia longitud la de uno es doble que la del otro ¿Qué relación existe entre sus peridos de osilacion R.-mucho depende de la masa si mes a la misma masa el de la distancia corta su periodo será mas corto y el de la mas larga será moyor a la de la otra. 10.-Dos esferas A y B de iguales masas cuelgan de hilos de longitud La=Lb e inician su movimiento en las posiciones que muestra la figura si oa=2ob ¿El periodo de A será el doble que el de B ¿ el triple ¿ la mitad Justifique su res`puesta. R.-sera el doble por que el tiempo de A será el doble que el de B y por esa razón será el doble VII. CONCLUSIONES.- En conclusiones se podría decir que hay varias formas de medir la magnitud de aceleración de la gravedad en esta oportunidad usamos un péndulo simple para medir aceleración de la gravedad que no fueron nuestros resultados tan exactos ya que en mismo experimento se presentan varios tipos de error y esos errores no dejaron sacar valor requerido. la la el el Y se pudo observa el Movimiento Armónico Simple en el péndulo simple y a su vez se pudo estudiar al péndulo y sus características se pudo determinar la ecuación experimental del péndulo simple. Mediante este experimento se pudo determinar la aceleración de la gravedad de diferentes formas con las ecuaciones que planteamos anteriormente el la practica. - 11 -