Números Reales: Clasificación, Aproximación y Operaciones
Anuncio
NÚMEROS REALES
Cristina García-Verdugo García
August 21, 2009
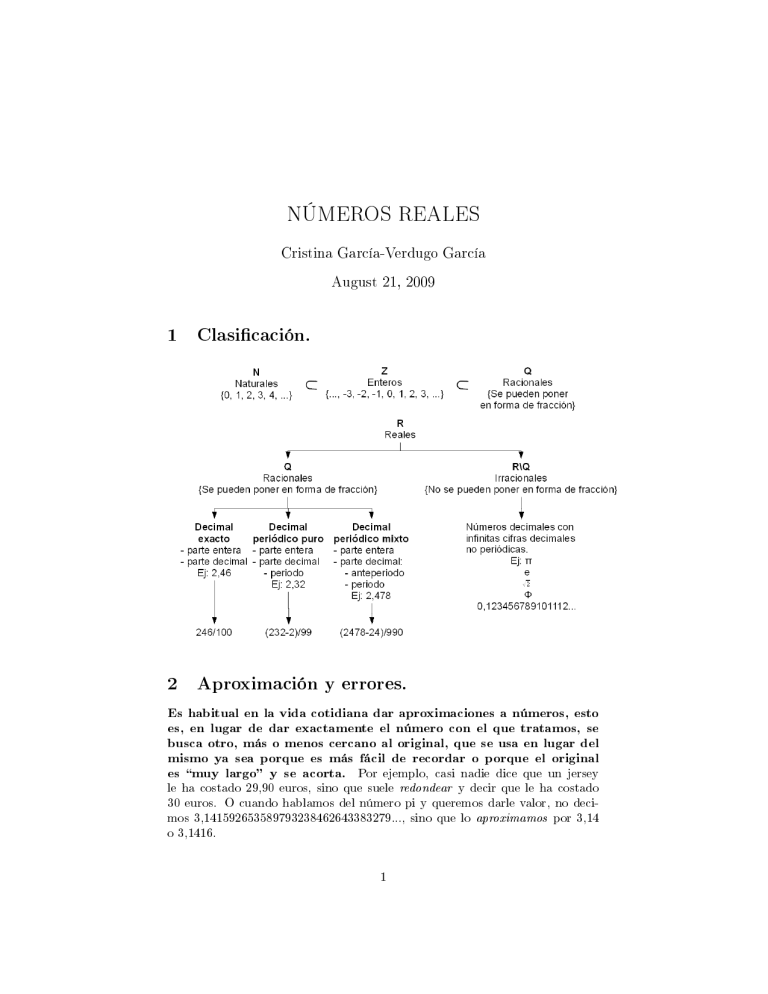
1 Clasicación.
2 Aproximación y errores.
Es habitual en la vida cotidiana dar aproximaciones a números, esto
es, en lugar de dar exactamente el número con el que tratamos, se
busca otro, más o menos cercano al original, que se usa en lugar del
mismo ya sea porque es más fácil de recordar o porque el original
es muy largo y se acorta. Por ejemplo, casi nadie dice que un jersey
le ha costado 29,90 euros, sino que suele redondear y decir que le ha costado
30 euros. O cuando hablamos del número pi y queremos darle valor, no decimos 3,141592653589793238462643383279..., sino que lo aproximamos por 3,14
o 3,1416.
1
2.1
Tipos de aproximación.
Existen dos clasicaciones de las aproximaciones:
Atendiendo a si la aproximación es mayor o menor que el número original:
Aproximación por defecto: Si el número con que se aproxima al
valor real u original es menor que este.
Aproximación por exceso: Si el número con que se aproxima al valor
real u original es mayor que este.
Ateniendo a hasta dónde se tiene en cuenta y cómo se trata la última cifra
decimal que se considera:
Aproximación por redondeo: Se eliminan las cifras a partir de un
orden considerado.
Aproximación por truncamiento: Al igual que con el redondeo, se
eliminan as cifras a partir de un orden considerado, pero la última
cifra con la que nos quedamos se aumenta en una unidad si la primera
eliminada es mayor o igual a 5.
Por ejemplo: consideremos de nuevo el número pi (π ): 3,141592653589793238462643383279...
- Algunas aproximaciones por defeco serían 3,14 , 3,1414 ó 3.
- Algunas aproximaciones por exceso serían 3,15 , 3,2 e incluso 4 (que por
cierto, sería una mala aproximación por estar un poco lejos del valor real de
\pi).
- Si truncamos a la cuarta cifra decimal obtenemos la aproximación 3,1415
- Si redondeamos a la cuarta cifra decimal obtenemos la aproximación 3,1416
2.2
Errores.
Está claro que cuando damos un número aproximado, al no ser exactamente el
número, se está cometiendo un error. Existen dos formas de medirlo:
Error absoluto:
Error relativo:
2.2.1
Ea = |vreal − vaproximado |
a
Er = |vE
real |
Números racionales.
Cuando se aproxima un número racional, estos errores se pueden calcular de
forma exacta. Por ejemplo:
Sea 2,33333.., decimal periódico puro que se puede expresar en forma fraccionaria y por lo tanto es racional. Para él, se da la aproximación 2,3. En este
a
23−3
= 20
9
9 y
error absoluto y el error relativo asociado es:
caso
vreal = 2, 3333... = 2, 3 =
vaproximado = 2, 3,
23
200−207
Ea = |vreal − vaproximado | = 20
=
9 − 10 =
90
7/90
Ea
7·9
7
Er = |vreal | = |20/9| = 20·90 = 200 = 0, 035
2
−7
90
=
7
90
por lo que el
_
= 0, 0 7
2.2.2
Números irracionales.
Sin embargo, los números irracionales tienen innitas cifras decimales no periódicas, por lo que el valor real no podríamos terminar de escribirlo nunca, por
lo que no se puede calcular el error exacto, sino tan sólo acotarlo, es decir, dar
un valor sabiendo que el error será menor que él.
Por ejemplo: Al aproximar
π
a las centésimas por truncamiento, obtenemos
el valor 3,14, en cuyo caso el error absoluto cometido es como mucho:
Ea = |vreal − vaproximado | = |π − 3, 14| = |3, 141592653589793238462643383279... − 3, 14| <
0, 005 = ε
0,005
ε
a
< vaproximado
Er = |vE
−ε = 3,14−0,005 = 0, 0016
real |
3 Potencias.
La denición de potencia de exponente natural para los números
reales, es la misma que para los números racionales: an = a · a · . . . · a
nveces
Se dene la potencia de un número real con exponente fraccionario como:
am/n =
√
n
am
Se dene la potencia de un número real con exponente negativo como:
a−n =
1
an
Respecto a las propiedades respecto a la operación de potencias, se
conservan las ya estudiadas para los números racionales:
an · am = an+m
an
am
= an−m
m
(an )
= an·m
n
an · bn = (a · b)
n
n
abn = ab
4 Radicales.
Dado un número real a, se llama
de
a , a todo número real b
raíz enésima de
que verique que
A dicho número real b se le llama
RADICANDO
a>0
√
n
a
a=0
a<0
a
bn = a,
o
radical de índice
y se escribe
√
a.
√
n
a.
n
b=n
valor numérico del radical
ÍNDICE
Nº DE RAÍCES REALES
n par
1 raíz positiva
n impar
2 raíces: una positiva y una negativa
n par o impar
1 raíz:
√
n
0=0
n par
1 raíz negativa
n impar
ninguna raíz
3
4.1
Radicales equivalentes. Utilidades.
Recuérdese que la expresion
am/n =
√
n
am ,
de modo que un radical se puede
expresar en forma de potencia y viceversa.
Se dice que dos radicales son
equivalentes cuando al expresarlos en forma
de potencia con exponente fraccionario, sus bases son iguales y sus exponentes
son fracciones equivalentes, i.e.:
√
p
am = am/n es equivalente a q ap = ap/q si m
n = q.
√
5
73 es equivalente a \sqrt[15]{7^{9}}
Por ejemplo:
√
n
ya que
3
5
=
9
15 .
Usando este concepto de radicales equivalentes, podemos simplicar radicales:
√
4
√
4
64 =
26 = 26/4 = 23/2 =
√
√
23 = 2 2
También nos sirve para reducir radicales a índice común:
√
√
3
√
6
7, se pueden expresar como 21/2 , 31/3 , 71/6 . Haciendo
m.c.m.(2,3,6)=6,
√
√
√
6
6
2/6
1/6
3
2
las potencias 2
, 3 , 7 son equivalentes, de modo que 2 , 3 , 6 7 son radSean
2,
3,
3/6
icales equivalentes a los iniciales con el mismo índice (6).
4.2
Operaciones entre radicales.
4.2.1
Suma y resta de radicales.
Para sumar o restar radicales, estos han de tener el mismo índice y radicando
en cuyo caso:
√
√
√
bna±cna=√
(b ± c)
· n a√
√
√
√
√
√
√
6
3
3
3
3
3
3
Por ejemplo: 3 5− 5+2 52 = 3 5− 5+2 5 = (3 − 1 + 2)
5 = 4 3 5.
4.2.2
Multiplicación y división de radicales.
Para multiplicar o dividir radicales, deben tener el mismo índice. Si no lo tienen,
se reducen a índice común y se operan:
√
√
a· nb= na·b
p
= n ab
√ √
√
1
1
2
1
2
3
Por ejemplo:
2 : 3 2 · 52 = 21/2 : 21/3 · 52/3 = 2 2 − 3 · 5 3 = 2 6 · 5 3 =
√
√
√
√
1
4
6
6
2 6 · 5 6 = 6 2 · 54 = 2 · 54 = 6 1250.
√
n
√
n a
√
n
b
4.2.3
Potenciación y radicación de radicales.
Para calcular la potencia o raíz de un radical, se transforman los radicales en
potencias y se opera usando las propiedades de las mismas.
Recordemos que
a
1
n·m
=
√
n·m
1 m
√ m
m
= an
( n a) = a n
y
p√
m
n
a =
a.
Por ejemplo:
p
√
7
3
5=
p
7
1 17
√
1
1
53 = 53
= 5 21 = 21 5.
4
p
m
1
an =
1
an
m1
=
4.3
Racionalización.
Dada una fracción con radicales en el denominador, racionalizarla es encontrar
otra fracción equivalente pero sin raíces en su denominador.
Hay dos tipos básicos de racionalización:
Si en el denominador hay una raíz simple, en cuyo caso se multiplica y
divide el denominador por la raiz de índice complementario hasta llegar a
la unidad:
a
√
n
b
√
n n−1
b
a· √
√
n
n
b· bn−1
=
3
√
5
2
Por ejemplo:
=
=
a·
√
n
√
5 4
2
3· √
√
5
5
2· 24
bn−1
b
=
3·
√
5
24
2
ó
−1
√
6
4· 72
=
√
6 4
7
−1·
√
√
6
6
4· 72 · 74
=
√
6
− 74
4·7
=
−
√
6 4
7
28 .
Si en el denominador la raíz o raíces aparecen junto con la operación de
suma o resta. En este caso, se multiplica numerador y denominador por
el conjugado del denominador:
a√
b+ c
=
b−
c
√
√
a·(b− c)
√
√
(b+ c)·(b− c)
√
ó
b±
2
Por ejemplo: √
√
3− 15
3−5
=
√
=
2−5
√
−3+ 15
.
2
=
√
a·(b− c)
(Idem si el denominador es de la forma
b2 −c
c).
(
√
√
2·( 2+5)
√
2−5)·( 2+5)
=
√
2 2+10
2−25
=
√
√
−2 2−10
3√
ó √
23
3+ 5
√
=
√
(
√ √
3·( 3− 5)
√
√ √
3+ 5)·( 3− 5)
5 Notación cientíca.
Se usa para representar y operar números con muchas cifras, en los que la
cantidad de ceros a la derecha (antes de la coma) o a la izquierda (después
de la coma) es muy grande.
Por ejemplo:
Masa de la Tierra
≈
5980000000000000000000000 kg.
Masa de un electrón≈ 0,00000000000000000000000000000091 kg.
La notación cientíca consiste en representar dichos números mediante un
mantisa, y una
orden de magnitud.
número decimal de una sola cifra entera al que se llama
potencia de 10 cuyo exponente se denomina
Por ejemplo:
9,1·10
−31
Masa de la Tierra
≈
24
5,98·10
, Masa de un electrón
≈
.
Para operar números expresados mediante notación cientíca, se aplican
las propiedades de las potencias. Así, el producto de la masa de la Tierra
5, 98 · 1024 · 9, 1 · 10−31 = (5, 98 · 9, 1) ·
= 5, 4418 · 10−6 .
y de un electrón da lugar a:
1024−31 = 54, 418 · 10−7
5
=
6 Ordenación.
Dados dos números reales a y b, se dice que
a es menor que b y se
a es mayor que b y se
escribe a <b si b-a >0. Por otro lado, se dice que
escribe a>b si b-a <0.
La relación de orden entre los números reales, cumple las siguientes propiedades:
Transitiva: Si
a≤b
y
b ≤ c,
entonces
a ≤ c.
Relación total: Dados dos números relaes a y b, o bien a<b ó a=b
ó a>b.
Monótona respecto a la suma: Si
a ≤ b,
entonces
(
Respecto al producto: Si
a ≤ b,
entonces
a + c ≤ b + c.
c>0 ⇒a·c≤b·c
.
c<0 ⇒a·c≥b·c
7 La recta real.
7.1
7.1.1
Representación de los números reales.
Números naturales y enteros.
Recordemos que para representar en la recta real un número natural o entero,
se marca el 0 y se toma como unidad un determinado segmento trasladándolo
en la recta tantas veces como el valor absoluto del número hacia la derecha del
0 si es positivo y hacia la izquierda si es negativo.
7.1.2
Números racionales.
Para representar los números racionales, se hace uso de la expresión mixta de
una fracción y del Teorema de Tales.
Por ejemplo:
8
3
=2+
2
3
6
7.1.3
Números irracionales.
La representación de los números irracionales se hace mediante una aproximación del número. En el caso de raíces cuadradas, se recurre al Teorema de
Pitágoras para su representación exacta.
Por ejemplo:
√
13 ⇒como 13 = 22 +32 ,
√
13 es la hipotenusa de un triángulo
rectángulo de catetos 2 y 3.
√
14 ⇒como 13 = 22 +32 +1,
√
14 es la hipotenusa de un triángulo rectángulo
de catetos 2 y 3, más una unidad.
7.2
Intervalos y semirrectas.
La relación de orden establecida para los números reales, permite denir algunos subconjuntos de números reales que tienen una interpretación geométrica
sencilla en la recta real.
7.2.1
Intervalos.
Conjunto de números reales comprendiddos entre dos números dados a y b a
los que se llama
extremos del intervalo. Dependiendo de si dichos números
a y b se cosideran o no dentro del conjunto, los intervalos se clasican como:
Intervalo
cerrado
[a, b] = {xR : a ≤ x ≤ b}.
Intervalo
abierto
(a, b) = {xR : a < x < b}.
Intervalo
abierto por la izquierda
7
(a, b] = {xR : a < x ≤ b}.
7.2.2
Intervalo
abierto por la derecha
[a, b) = {xR : a ≤ x < b}.
Semirrectas.
Cuando uno de los extremos del intervalo es el imnito,
una semirrecta.
(±∞),
se dice que es
En función de si el extremo no innito se incluye o no en el
conjunto, se habla de semirrecta cerrada o abierta, respectivamente.
Semirrecta abierta
(a, +∞) = {xR : x > a}
ó
(−∞, a) = {xR : x < a}
Semirrecta cerrada
[a, +∞) = {xR : x ≥ a}
ó
(−∞, a] = {xR : x ≤ a}
8 Valor absoluto.
Por último, extender a los números reales la denición de valor absoluto que ya
se conoce para los números racionales:
(
+a
|a| =
−a
si a ≥ 0
si a < 0
8