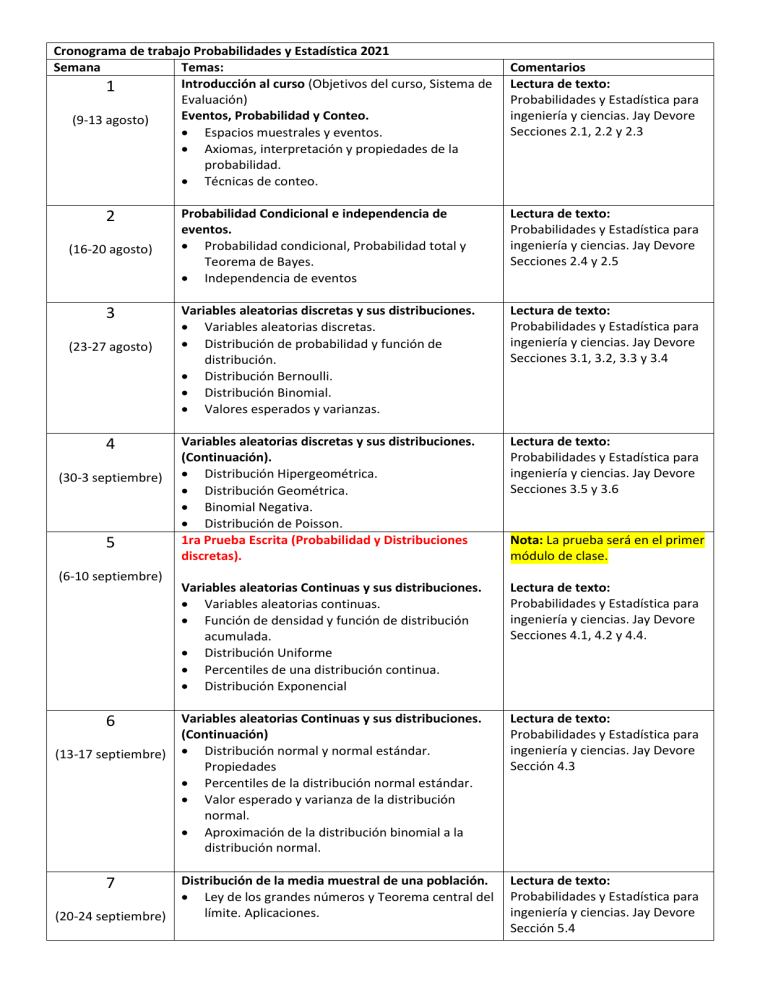
Cronograma de trabajo Probabilidades y Estadística 2021 Semana Temas: Introducción al curso (Objetivos del curso, Sistema de 1 Evaluación) Eventos, Probabilidad y Conteo. (9-13 agosto) • Espacios muestrales y eventos. • Axiomas, interpretación y propiedades de la probabilidad. • Técnicas de conteo. 2 (16-20 agosto) 3 (23-27 agosto) 4 (30-3 septiembre) 5 (6-10 septiembre) 6 (13-17 septiembre) 7 (20-24 septiembre) Comentarios Lectura de texto: Probabilidades y Estadística para ingeniería y ciencias. Jay Devore Secciones 2.1, 2.2 y 2.3 Probabilidad Condicional e independencia de eventos. • Probabilidad condicional, Probabilidad total y Teorema de Bayes. • Independencia de eventos Lectura de texto: Probabilidades y Estadística para ingeniería y ciencias. Jay Devore Secciones 2.4 y 2.5 Variables aleatorias discretas y sus distribuciones. • Variables aleatorias discretas. • Distribución de probabilidad y función de distribución. • Distribución Bernoulli. • Distribución Binomial. • Valores esperados y varianzas. Lectura de texto: Probabilidades y Estadística para ingeniería y ciencias. Jay Devore Secciones 3.1, 3.2, 3.3 y 3.4 Variables aleatorias discretas y sus distribuciones. (Continuación). • Distribución Hipergeométrica. • Distribución Geométrica. • Binomial Negativa. • Distribución de Poisson. 1ra Prueba Escrita (Probabilidad y Distribuciones discretas). Lectura de texto: Probabilidades y Estadística para ingeniería y ciencias. Jay Devore Secciones 3.5 y 3.6 Variables aleatorias Continuas y sus distribuciones. • Variables aleatorias continuas. • Función de densidad y función de distribución acumulada. • Distribución Uniforme • Percentiles de una distribución continua. • Distribución Exponencial Lectura de texto: Probabilidades y Estadística para ingeniería y ciencias. Jay Devore Secciones 4.1, 4.2 y 4.4. Variables aleatorias Continuas y sus distribuciones. (Continuación) • Distribución normal y normal estándar. Propiedades • Percentiles de la distribución normal estándar. • Valor esperado y varianza de la distribución normal. • Aproximación de la distribución binomial a la distribución normal. Lectura de texto: Probabilidades y Estadística para ingeniería y ciencias. Jay Devore Sección 4.3 Distribución de la media muestral de una población. • Ley de los grandes números y Teorema central del límite. Aplicaciones. Lectura de texto: Probabilidades y Estadística para ingeniería y ciencias. Jay Devore Sección 5.4 Nota: La prueba será en el primer módulo de clase. 8 (27-1 octubre) 9 (4-8 octubre) 10 (11-15 octubre) Distribuciones conjuntas y variables aleatorias independientes. • Distribución conjunta de variables aleatorias discretas. • Distribución conjunta de variables aleatorias continuas. • Variables aleatorias independientes. • Distribución condicional conjunta. • Valores esperados, varianza, covarianza y correlación de variables aleatorias. Semana UCU ENTREGA Y DEFENSA DEL 1er PROYECTO DE EVALUACIÓN Estimación puntual de parámetros. • Características de los estimadores. • Estimadores insesgados y de varianza mínima. • Método de los momentos. • Estimador de máxima verosimilitud. 11 (18-22 octubre) 12 (25-29 octubre) 13 Lectura de texto: Probabilidades y Estadística para ingeniería y ciencias. Jay Devore Secciones 5.1 y 5.2 Nota: Para la carrera de informática, este tema solo se estudiará para el caso de la distribución conjunta de variables discretas. No hay clases Observación: La defensa será el día de clase de cada grupo, en el horario de clase correspondiente. Lectura de texto: Probabilidades y Estadística para ingeniería y ciencias. Jay Devore Secciones 6.1 y 6.2 Estimación por intervalos para una muestra de una población. • Propiedades de los intervalos de confianza. • Intervalos de confianza para la media y la proporción de una población con muestra grande. • Distribución t-student y sus propiedades. • Intervalos de confianza para la media de una población normal con varianza conocida y desconocida. • Intervalos de confianza para la varianza y la desviación estándar de una población. Lectura de texto: Probabilidades y Estadística para ingeniería y ciencias. Jay Devore Secciones 7.1, 7.2, 7.3 y 7.4 2da Prueba Escrita (Variables continuas, Distribución conjunta y Estimación puntual) Nota: La prueba será en el primer módulo de clase y se evaluarán los contenidos estudiados entre las semanas 5 y 10. Test de hipótesis paramétricas. • Hipótesis y tipos de errores. • Test de hipótesis para la media de una población normal. • Test de hipótesis para la media de una población con muestra grande. Test de hipótesis para la proporción de una población. Análisis del p-valor en los test de hipótesis. • El p-valor en el test de hipótesis cuando se utiliza la distribución normal estándar. • El p-valor en el test de hipótesis cuando se utiliza la distribución t-student. Lectura de texto: Probabilidades y Estadística para ingeniería y ciencias. Jay Devore Secciones 8.1, 8.2 y 8.3 Lectura de texto: Probabilidades y Estadística para ingeniería y ciencias. Jay Devore Sección 8.4 (1-5 noviembre) 14 (8-12 noviembre) 15 (15-19 noviembre) 16 Test de hipótesis y estimación por intervalos para dos muestras de dos poblaciones (Pruebas Z). • Test de hipótesis para la diferencia de medias de dos poblaciones con varianzas conocidas. • Test de hipótesis para la diferencia de medias de dos poblaciones con muestras grandes. • Error Beta y tamaño de muestra. • Intervalos de confianza para diferencia de medias de dos poblaciones. Lectura de texto: Probabilidades y Estadística para ingeniería y ciencias. Jay Devore Secciones 9.1 Test de hipótesis y estimación por intervalos para dos muestras de dos poblaciones (Pruebas t). • Test de hipótesis para la diferencia de medias de dos poblaciones con varianzas desconocidas. Datos agrupados y no agrupados. • Intervalos de confianza para diferencia de medias de dos poblaciones. • Test de comparación de varianzas. Lectura de texto: Probabilidades y Estadística para ingeniería y ciencias. Jay Devore Secciones 9.2 y 9.5 • (22-26 noviembre) ENTREGA Y DEFENSA DEL 2do PROYECTO DE EVALUACIÓN Elaborado por: Docentes del curso: MSc. Dainel Arzuaga Rodríguez Lic. Sebastián Decuadro Observación: La defensa será el día de clase de cada grupo, en el horario de clase correspondiente.









