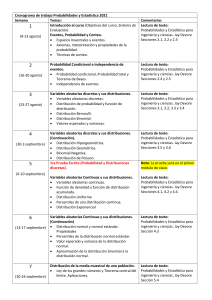
programa analítico y cronograma

DEPARTAMENTO DE CIENCIA Y TECNOLOGIA
UNIVERSIDAD NACIONAL DE QUILMES
Roque Saenz Peña 180 – (B1876BXD) Bernal – Buenos Aires – Argentina
1- CARRERA: Diplomatura en Ciencia y Tecnología
2- AÑO /CUATRIMESTRE: 2007/Primer cuatrimestre
3- NOMBRE DE LA ASIGNATURA: Probabilidades y Estadística A
4- NOMBRE DEL PROFESOR: Jorge Gastón Argeri
5- NÚCLEO AL QUE PERTENECE LA MATERIA: Obligatorio
6- AREA DE CONOCIMIENTO: Matemática
7- TIPO DE ASIGNATURA: Teórico-práctica
8- CRÉDITOS: 10
9- CARGA HORARIA SEMANAL: 6 horas
10- OBJETIVOS DEL CURSO:







Utilizar estimadores de posición, dispersión y correlación, robustos y no robustos.
Utilizar distintas técnicas de análisis exploratorio: histogramas, diagramas tallohoja, diagramas de caja, Q-Q plots.
Abordar situaciones (experimentos aleatorios) en las que está involucrado el azar,
conocer y aplicar modelos probabilísticos (sus alcances, propiedades y
consecuencias) que permitan una adecuada interpretación de tales experimentos.
Incorporar y utilizar los conceptos de variable aleatoria, distribución y densidad de
probabilidad, esperanza, varianza y covarianza (momentos), así como sus
propiedades básicas. Conocer distintos tipos de convergencia de sucesiones de
variables aleatorias.
Conocer y aplicar la Ley de los Grandes Números y el Teorema Central del Límite.
Estimar características poblacionales mediante estadísticos, utilizando distintos
métodos de estimación puntual. Obtener intervalos de confianza para parámetros
de una distribución. Estimar simultáneamente.Testear hipótesis estadísticas.
Conocer los significados de p-valor y potencia de un test.
Conocer y aplicar modelos de regresión lineal. Analizar supuestos del modelo.
Utilizar algunos tests no paramétricos.
11- MODALIDAD: Presencial
1
DEPARTAMENTO DE CIENCIA Y TECNOLOGIA
UNIVERSIDAD NACIONAL DE QUILMES
Roque Saenz Peña 180 – (B1876BXD) Bernal – Buenos Aires – Argentina
12- CONOCIMIENTOS O COMPETENCIAS PREVIOS: Análisis Matemático I, Álgebra y
Geometría Analítica, Análisis Matemático II. Sería óptimo si los alumnos hubieran cursado
Análisis Matemático III (integrales dobles, sucesiones y series).
13- CONTENIDOS MÍNIMOS:
Estadística Descriptiva. Modelos determinísticos y estocásticos. Distribuciones de
probabilidad sobre un espacio muestral. Variables aleatorias discretas y continuas.
Distintos tipos de distribuciones.Inferencia estadística. Intervalos de confianza. Varianza.
Regresión lineal. Coeficientes de correlación. Tests de hipótesis.
14- PROGRAMA ANALÍTICO:
Unidad 1:
Experimentos aleatorios. Espacio muestral. Sigma-álgebras. Eventos. Motivación
frecuentista de la noción de probabilidad. Axiomas de probabilidad. Espacios de
equiprobabilidad.
Unidad 2:
Independencia de eventos. Probabilidad condicional. Regla de la multiplicación.Teorema
de la probabilidad total y regla de Bayes.
Unidad 3:
Variables aleatorias discretas y continuas. Función de distribución y función de densidad
de probabilidad. Cuantiles de una distribución. Funciones de variables aleatorias. Familias
paramétricas de distribuciones: binomial, geométrica, Poisson, hipergeométrica, binomial
negativa, uniforme, gaussiana, Gamma, Beta, Cauchy, LogNormal, Doble Exponencial, t de
Student, chi-cuadrado, Fisher, Weibull. Propiedades básicas de la distribución gaussiana.
Unidad 4:
Vectores aleatorios discretos y continuos. Distribución conjunta y distribuciones
marginales. Distribuciones condicionales. Independencia de variables aleatorias.Teorema
de cambio de variables.
Unidad 5:
Esperanza, varianza y covarianza. Propiedades. Desigualdades de Chebyshev y Markov.
Momentos de una distribución.
Unidad 6:
Estadística descriptiva. Diagramas tallo-hoja, histogramas, polígonos de frecuencia,
diagramas de caja. Medidas de posición y dispersión. Q-Q plots.
Unidad 7:
Teoría asintótica.Tipos de convergencia de sucesiones de variables aleatorias, Ley de los
Grandes Números, Teorema Central del Límite. Aproximación normal a la distribución
binomial.
Unidad 8:
Noción de estimador. Error cuadrático medio. Sesgo. Estimación puntual: Método de los
momentos, método de máxima verosimilitud, método de mínimos cuadrados. Métodos no
2
DEPARTAMENTO DE CIENCIA Y TECNOLOGIA
UNIVERSIDAD NACIONAL DE QUILMES
Roque Saenz Peña 180 – (B1876BXD) Bernal – Buenos Aires – Argentina
paramétricos. Estimadores insesgados. Intervalos de confianza exactos y asintóticos para
un parámetro poblacional. Estimación puntual e intervalos de confianza para una media y
una proporción poblacional y para una diferencia de medias. Intervalos de confianza de
nivel simultáneo.
Unidad 9:
Formulación general del problema de tests de hipótesis. Tipos de errores. Potencia de un
test. Nivel de significación y p-valor de un test. Tests asintóticos. Test para la media y
para diferencia de medias, tests binomiales, test para diferencia de proporciones, test para
comparación de varianzas.
Unidad 10:
Modelo de regresión lineal simple. Recta de regresión. Estimación de la pendiente y del
intercept por cuadrados mínimos. Distribución de los estimadores e intervalos de confianza
para los mismos. Correlación. Estadístico R2 para comparar ajuste.
15- FORMA DE EVALUACIÓN:
Condiciones de aprobación:
 Cumplir con una asistencia no inferior al 75%.
 Aprobar dos parciales teórico – prácticos (P1 y P2) (o sus correspondientes
recuperatorios RP1 y RP2) con notas iguales o superiores a 5 puntos. La forma de
asignar notas a ambos parciales se explica más abajo.
 En caso de aprobar los dos parciales (o sus recuperatorios) con puntaje no inferior
a 7 puntos cada uno, el alumno promociona la materia. En caso que el alumno
aprobara alguno o los dos parciales con al menos 5 y menos de 7 puntos, debe
rendir un final (F) integrador teórico-práctico. En otros casos el alumno desaprueba
la materia.
 La nota asignada a cada parcial se calculará del modo siguiente:
(Nota parcial)=0,1*(Nota 1ra.fecha)+0,9*(Nota recuperatorio)

Eventualmente se podrá incluir la entrega de trabajos de laboratorio.
16- CRONOGRAMA TENTATIVO:
P1: jueves 3 de mayo, 9h.
RP1: sábado 19 de mayo, horario y aula a determinar.
P2: jueves 28 de junio, 9h.
RP2: sábado 7 de julio, horario y aula a determinar.
F: martes 10 de julio, 9h.
17- BIBLIOGRAFÍA RECOMENDADA:
• Devore, Jay. “Probabilidad y Estadística para Ingeniería y Ciencias”.
International Thompson.
3
DEPARTAMENTO DE CIENCIA Y TECNOLOGIA
UNIVERSIDAD NACIONAL DE QUILMES
Roque Saenz Peña 180 – (B1876BXD) Bernal – Buenos Aires – Argentina
•
•
•
•
Cramer,H. “Elementos de la Teoría de Probabilidades”. Ed Aguilar.
Feller,W. “Introducción a la Teoría de Probabilidades y sus Aplicaciones”. Ed Limusa.
Parzen, E. “Teoría Moderna de Probabilidades y sus Aplicaciones”. Ed. Limusa.
Marona, “Probabilidad y Estadística elementales para estudiantes de
ciencias”. Editorial Exacta.
• Meyer, Paul. “Probabilidad y Aplicaciones Estadísticas”. Addison Wesley
Iberoamericana.
• Santaló, Luis. “Probabilidad e Inferencia estadística”. Monografía Nº 11,
Serie Matemática. Editorial EUDEBA.
• DeGroot, Morris. “Probabilidad y Estadística”. Addison Wesley
Iberoamericana.
 Tucker, H. “Introducción a la Teoría Matemática de las Probabilidades y la Estadística”,
Academic Press, New York.
18- BIBLIOGRAFÍA DE CONSULTA:
 Box, Hunter y Hunter. “Estadística para Investigadores”. Editorial
Reverté.
 Casella, George – Berger Roger, “Statistical Inferece”. Duxbury Press.
 Ross, Sheldon. “A First Course in Probability. Macmillian. New York.
 Ross, Sheldon. “Introduction to Probability Models”. Academia Press
19- HORAS DE ESTUDIO RECOMENDADAS FUERA DEL AULA: 9
20- CURRICULUM ABREVIADO DEL DOCENTE A CARGO DEL CURSO:
Licenciado en Matemática, Universidad Nacional de La Plata (1995). Ex docente del
Departamento de Matemática de la Facultad de Ciencias Exactas y de la Facultad de
Ingeniería de la Universidad Nacional de La Plata. Profesor contratado por la Universidad
Nacional de Quilmes desde 2001 hasta mediados de 2004. Instructor ordinario (desde
mediados de 2004) en área matemática de la Universidad Nacional de Quilmes Cursos de
postgrado en las áreas de Lógica-Matemática y Álgebra en la Universidad de Montreal,
Canadá. Actualmente con estudios avanzados del postgrado Maestría en Estadística
Matemática de la Universidad de Buenos Aires.
21-
E MAIL DEL DOCENTE:
[email protected]
4