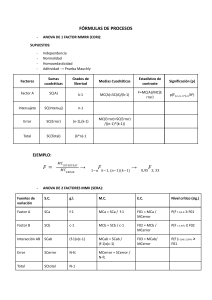
Fórmulas de Diseño Experimental: ANOVA y Pruebas de Comparación
Anuncio

FÓRMULAS Diseño completamente al azar Tabla de análisis de varianza. Fuente de variación Grados de libertad Suma de cuadrados Debido a los tratamientos 𝑆𝐶𝑇𝑟𝑎𝑡 = 𝑦 𝑦 − 𝑛 𝑁 𝑎−1 Cuadrados medio 𝐶𝑀𝑇𝑟𝑎𝑡 = F0 𝑆𝐶𝑇𝑟𝑎𝑡 𝑎−1 𝐹 = Debido al error 𝑆𝐶𝐸 = Total 𝑆𝐶𝑇 = 𝑦 −𝑦 𝑦 − 𝑆𝐶𝐸 𝐶𝑀𝐸 = 𝑎(𝑛 − 1) 𝑎(𝑛 − 1) 𝑦 𝑁 𝐶𝑀𝑇𝑟𝑎𝑡 𝐶𝑀𝐸 𝑎𝑛 − 1 n = número de repeticiones del tratamiento a = número de tratamientos donde: 𝑦 = 𝑦 = ∑ 𝑦 : Promedio de las observaciones bajo el i-ésimo tratamiento. 𝑛 𝑦 = 𝑦 = : Total de observaciones del i-ésimo tratamiento. 𝑦 : Suma total de observaciones. 𝑦 𝑦 ∑ = 𝑁 ∑ 𝑁 𝑦 : Promedio general. Estimación de los parámetros del modelo 𝜇̂ = 𝑦 𝜇̂ = 𝑦 = ∑ 𝑦 𝜏̂ = 𝑦 − 𝑦 Intervalo de confianza para los parámetros del modelo a. El intervalo de confianza para 𝜇 con un nivel de confianza (1 - ) es: 𝜇 ∈ ⟨𝑦 ± 𝑡 ⁄ , ( ) 𝐶𝑀𝐸 ⟩ 𝑛 Fc 𝐹 , ( ) b. El intervalo de confianza para 𝜇 − 𝜇 con un nivel de confianza de (1 - ) es: Si el número de repeticiones de cada tratamiento es igual: (𝜇 − 𝜇 ) ∈ ⟨𝑦 − 𝑦 ± 𝑡 ⁄ , ( ) 2𝐶𝑀𝐸 ⟩ 𝑛 Si el número de repeticiones de cada tratamiento es diferente: (𝜇 − 𝜇 ) ∈ ⟨𝑦 − 𝑦 ± 𝑡 ( ⁄ , ) 𝐶𝑀𝐸 1 1 ⟩ + 𝑛 𝑛 Pruebas de comparación Prueba LSD (diferencia mínima significativa) 𝑌 − 𝑌 > 𝑡 ⁄ , 𝐿𝑆𝐷 = 𝑡 ( ⁄ , 1 1 + 𝑛 𝑛 𝐶𝑀𝐸 ) ( ) 2𝐶𝑀𝐸 𝑛 Prueba de Tuckey 𝑇 = 𝑞 𝑘, 𝑎(𝑛 − 1) 𝐶𝑀𝐸 𝑛 = 𝐿𝑆𝐷 Diseño de bloques completo al azar (DBCA) Arreglo de los datos en bloques completos al azar Tratamiento Bloque 1 2 3 … b 1 𝑌 𝑌 𝑌 … 𝑌 2 𝑌 𝑌 𝑌 … 𝑌 3 𝑌 𝑌 𝑌 … 𝑌 . . . . . . . . . . . . k 𝑌 𝑌 𝑌 . . . . . . … 𝑌 Análisis de varianza ANOVA para un diseño en bloques completos al azar. Fuente de variabilidad Suma de cuadrados Grados de libertad Cuadrado medio Tratamientos SCTrat k-1 CMTrat Bloques SCB b-1 CMB Error SCE (k-1) (b-1) CME SCT N-1 Total 𝑌 𝑁 𝑌 − 𝑆𝐶𝑇𝑟𝑎𝑡 = 𝑌 𝑌 − 𝑏 𝑁 𝑌 𝑘 − 𝐹 = 𝑌 𝑁 y la del error se obtiene por sustracción como: 𝑆𝐶𝐸 = 𝑆𝐶𝑇 − 𝑆𝐶𝑇𝑟𝑎𝑡 − 𝑆𝐶𝐵 Fc 𝐶𝑀𝑇𝑟𝑎𝑡 𝐶𝑀𝐸 𝐹 , ,( )( ) 𝐶𝑀𝐵 𝐶𝑀𝐸 𝐹 , ,( )( ) 𝐹 = 𝑆𝐶𝑇 = 𝑆𝐶𝐵 = F0 Comparación de parejas de medias de tratamiento en el DBCA. Prueba LSD (diferencia mínima significativa) 𝐿𝑆𝐷 = 𝑡 ⁄ ,( )( ) 2𝐶𝑀𝐸 𝑏 Prueba de Tukey 𝑇𝛼 = 𝑞𝛼 𝑘, (𝑘 − 1)(𝑏 − 1) donde: 𝑏 = Número de bloques (𝑘 − 1)(𝑏 − 1) = Grados de libertad del CME 𝐶𝑀𝐸 𝑏 Diseño en cuadro latino ANOVA para el diseño de cuadro latino. Bloque II (columnas) 1 Bloque I (renglones) 2 3 … k 1 𝐴=𝑌 𝐵=𝑌 𝐶=𝑌 … 𝐾=𝑌 2 𝐵=𝑌 𝐶=𝑌 𝐷=𝑌 … 𝐴=𝑌 3 𝐶=𝑌 𝐷=𝑌 𝐸=𝑌 … 𝐵=𝑌 . . . k . . . . . . 𝐾=𝑌 . . . 𝐴=𝑌 . . . … 𝐵=𝑌 . . . 𝐽=𝑌 Análisis de varianza Fuente de variabilidad Suma de cuadrados Grados de libertad Cuadrado medio SCTrat k-1 CMTrat Renglones SCB1 k-1 CMB1 Columnas SCB2 k–1 CMB2 Error SCE (k – 2) ( k – 1) CME Total SCT k2 - 1 Tratamientos 𝑆𝐶𝑇 = 𝑆𝐶𝑇𝑟𝑎𝑡 = 𝑆𝐶𝐵 = 𝑆𝐶𝐵 = 𝑌 − 𝐹 𝐶𝑀𝑇𝑟𝑎𝑡 𝐶𝑀𝐸 𝐹 ,( )( ) 𝐹 = 𝐶𝑀𝐵 𝐶𝑀𝐸 𝐹 ,( )( ) 𝐹 = 𝐶𝑀𝐵 𝐶𝑀𝐸 𝐹 ,( )( ) 𝐹 = 𝑌 𝑁 𝑌 𝑌 − 𝑘 𝑁 𝑌 𝑘 − 𝐹 𝑌 𝑁 𝑌 𝑌 − 𝑘 𝑁 𝑆𝐶𝐸 = 𝑆𝐶𝑇 − 𝑆𝐶𝑇𝑟𝑎𝑡 − 𝑆𝐶𝐵 − 𝑆𝐶𝐵 Diseño en cuadro grecolatino Diseño en cuadro grecolatino. Columnas Renglones 1 2 3 4 1 𝐴𝛼 𝐵𝛽 𝐶𝛾 𝐷𝛿 2 𝐵𝛿 𝐴𝛾 𝐷𝛽 𝐶𝛼 3 𝐶𝛽 𝐷𝛼 𝐴𝛿 𝐵𝛾 4 𝐷𝛾 𝐶𝛿 𝐵𝛼 𝐴𝛽 Los tratamientos pueden estar asignados a los renglones, columnas, letras griegas o latinas. ANOVA para el diseño en cuadro grecolatino. Fuente de variabilidad Suma de cuadrados Grados de libertad Cuadrado medio SCTrat k-1 CMTrat Factor de bloque I SCB1 k-1 CMB1 Factor de bloque II SCB2 k–1 Factor de bloque III SCB3 Error Total Tratamientos 𝐹 𝐹 𝐶𝑀𝑇𝑟𝑎𝑡 𝐶𝑀𝐸 𝐹 ,( )( ) 𝐹 = 𝐶𝑀𝐵 𝐶𝑀𝐸 𝐹 ,( )( ) CMB2 𝐹 = 𝐶𝑀𝐵 𝐶𝑀𝐸 𝐹 ,( )( ) k–1 CMB3 𝐹 = 𝐶𝑀𝐵 𝐶𝑀𝐸 𝐹 ,( )( ) SCE (k – 3) ( k – 1) CME SCT k2 – 1 𝑆𝐶𝑇 = 𝑆𝐶𝑇𝑟𝑎𝑡 = 𝑌 𝐹 = − 𝑌 𝑁 𝑌 𝑌 − 𝑘 𝑁 𝑆𝐶𝐵 = 𝑌 𝑌 − 𝑘 𝑁 𝑆𝐶𝐵 = 𝑌 𝑌 − 𝑘 𝑁 𝑆𝐶𝐵 = 𝑌 𝑌 − 𝑘 𝑁 𝑆𝐶𝐸 = 𝑆𝐶𝑇 − 𝑆𝐶𝑇𝑟𝑎𝑡 − 𝑆𝐶𝐵 − 𝑆𝐶𝐵 − 𝑆𝐶𝐵