Ejemplo de un cuadrado greco

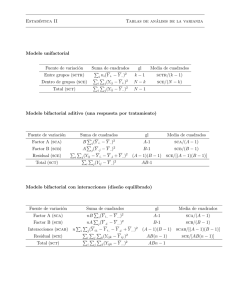
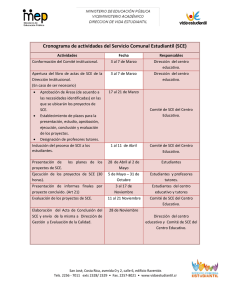
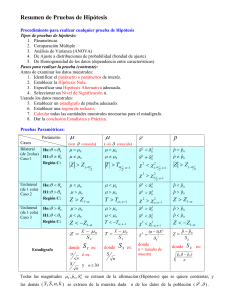
Ejemplo de un cuadrado greco-latino (Peña, 2002)
Se compara el rendimiento de tres procesos de fabricación (A,B, C) en tres
condiciones experimentales (α, β, γ) tres dı́as distintos con tres procedimientos
de medición. El diseño y los resultados obtenidos se indican en el cuadro. El
número entre paréntesis en cada casilla es la media de las dos replicaciones.
Dı́a 1
Dı́a 1
Dı́a 1
Método 1
Aα
9, 11
(10)
Bβ
12,14
(13)
Cγ
11,11
(11)
Método 2
Cβ
6, 10
(8)
Aγ
8, 8
(8)
Bα
11, 9
(10)
Método 3
Bγ
9, 9
(9)
Cα
13, 9
(11)
Aβ
10, 10
(10)
El modelo matemático:
yijkj = µ + αi + βj + γk + δh + ijkh
Los estimadores son:
µ̂ = ȳ.... = 10,
α̂i = ȳi... − ȳ.... = (1.33, −1.33, 0),
β̂j = ȳ.j.. − ȳ.... = (−1, 0.67, 0.33),
γ̂k = ȳ..k. − ȳ.... = (−0.67, 0.67, 0),
δ̂h = ȳ...h − ȳ.... = (0.33, 0.33, −0.66).
Las sumas de cuadrados:
SCE =
X
(yijkh − ȳi... − ȳ.j.. − ȳ..k. − ȳ...h + 3ȳ.... )2 = 2I 2 − 4I + 3σ̂ 2
ijkh
La tabla ANOVA es
F actor
SC
P 2
2
Ef ectof ila(A)
I ȳi... − I 2 ȳ....
P 2
2
Ef ectocolumna(B) I ȳ.j.. − I 2 ȳ....
P 2
2
Letralatina(C)
I ȳ..k. − I 2 ȳ....
P 2
2
Letragriega(D)
I ȳ...h − I 2 ȳ....
Error
SCE
T otal
1
g.l.
MC
F
I −1
SCA/(I − 1)
M CA/M CE
I −1
SCB/(I − 1)
M CB/M CE
I −1
SCC/(I − 1)
M CC/M CE
I −1
SCD/(I − 1)
M CD/M CE
2I 2 − 4I + 3 SCE/2I 2 − 4I + 3
2I 2 − 1
En nuestro ejemplo I = 3, la tabla ANOVA es
Factor
Metodo (Fila A)
Dı́as (Columna B)
Letra latina (C)
Letra griega (D)
Error
Total
SC
g.l.
MC
F
21.23
9.36
5.39
4.02
22
62
2
2
2
2
9
17
10.62
4.68
2.70
2.01
2.44
4.35
1.92
1.11
0.82
La región de rechazo es RR = [4.26, ∞) y por lo tanto el único efecto significativo es el del método.
2