TEMA 63.Frecuencia y azar. Leyes de azar. Espacio probabilístico
TEMA 63. Frecuencia y Azar. Leyes de Azar. Espacio probabilístico.
1. Introducción.
1.1 Histórica.
Los conceptos de azar e incertidumbre son tan viejos como la propia civilización. La humanidad siempre ha debido soportar la incertidumbre del clima, de las cosechas y otros aspectos
de medio que lo rodea, así como buscar los efectos que los regulan para tratar de reducir las
probabilidades que generan efectos negativos.
El origen de la probabilidad desde un punto de vista matemático se cree que surge con los
juegos de azar. Así en el Egipto antiguo ( 3500 aC) se tiene constancia de la existencia de juegos de azar practicado con objetos de hueso, siendo estos los predecesores de los dados actuales. También los egipcios construyeron dados con marcas como los actuales.
Se suele aceptar como el comienzo de la teoría matemática de la probabilidad con Fermat
y Pascal, matemáticos franceses del siglo XVIII. Estos lograron calcular la probabilidad exacta
para ciertos juegos de azar relacionados con los dados. Desde este momento la teoría de la
probabilidad ha sido constantemente desarrollada y aplicada a más diversos campos de estudio.
En la actualidad la teoría de la probabilidad es una herramienta importante en la mayoría
de las ingenierías, en ciencias de la naturaleza y en economía. Aplicándose en procesos como
la meteorología, medicina, predicción de terremotos, estudio de la evolución de especies, en
cultivos, comportamiento humano….
1.2 Experimentos aleatorios y deterministas.
Los fenómenos naturales o los diferentes fenómenos de estudio pueden identificarse en:
a) Fenómenos o experimentos deterministas: son aquellos que bajo unas mismas condiciones iniciales el resultado siempre es el mismo. Por ejemplo la evaporación del agua
que siempre se produce a 100o y 1 Atm o multitud de otros fenómenos físicos o químicos.
b) Fenómenos o experimentos aleatorios: el resultado es incierto aun cuando se pueden
fijar las condiciones iniciales. Por ejemplo el resultado al lanzar un dado o el resultado
de un partido de tenis.
c) Fenómenos pseudoaleatorios: son fenómenos deterministas pero que dependen mucho de las condiciones iniciales. Así una pequeña variación de las condiciones iniciales
puede influir enormemente en el resultado final. Esto ocurre por ejemplo en la predicción meteorológica. Es lo que vulgarmente se conoce como efecto mariposa: “un batir
de las alas de una mariposa en Pekín puede hacer que llueva en Nueva York”. Otros
fenómenos de esta índole son los terremotos, el crecimiento de un árbol, etc. Estos
fenómenos tienen cabida en el estudio de la probabilidad. Así se utiliza esta palabra
para explicar sus resultados (probabilidad de lluvia).
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
1
TEMA 63.Frecuencia y azar. Leyes de azar. Espacio probabilístico
2. Definición de probabilidad.
Aunque el concepto de probabilidad es muy intuitivo, su definición precisa no es ni mucho
menos sencilla.
La probabilidad clásica, o también conocida como de Laplace establece que la probabilidad de un suceso es igual al cociente del número de casos favorables ente el número de sucesos totales, siempre que todos los sucesos sean equiprobables.
p( suceso) =
n ºsuceos favorables
nº sucesos totales
Así si lanzamos una moneda con 6 caras iguales la probabilidad de sacar un número cualquiera será de 1/6.
Sin embargo cuando lanzamos dos monedas y contamos el número de caras, que pueden
ser 0,1 o 2, la probabilidad ahora no es de 1/3 porque es más sencillo que salga una cara que
las otras dos opciones (ya que puede ocurrir de dos maneras, cara y cruz o cruz y cara). Para
estos casos habrá que buscar los sucesos que sean equiprobables: {xx, cc, cx,xc} siendo ahora
la probabilidad de 1 cara igual a 2/4 o ½.
Para aplicar la definición es necesario saber el número de los casos favorables y posibles,
ocupándose de esto la teoría de la combinatoria.
Esta definición tiene un gran problema, el concepto de equiprobables. ¿Cómo podemos
asegurar que dos o más sucesos tienen la misma probabilidad?. Parece que la simetría del
problema en este sentido tiene mucho que ver, por ejemplo si las caras de un cubo no se pueden distinguir una de otras parece lógico que la probabilidad de que caigan en una u otra cara
es la misma. Pero esto no se puede aplicar fuera de los juegos de azar, por ejemplo el cálculo
de la probabilidad de que una chincheta caiga de una u otra forma (ya no son simétricas).
Probabilidad empírica (Ley de grandes números): válida cuando estudiamos un experimento que puede repetirse en el mismo contexto tantas veces como se desee. Si A es un suceso (conjunto de resultados posibles) llamaremos frecuencia absoluta del suceso, fA, al número
de veces que ocurre este suceso. Siendo la frecuencia relativa, frA el cociente entre la absoluta
y el número de veces realizado el experimento. La “Ley de azar” establece que la frecuencia
relativa tiende a estabilizarse cuando aumentamos el número de experimentos, siendo este
número cuando n tiene a infinito el que identificamos con la probabilidad de un suceso:
p ( A) = lim f r ( A) = lim
n →∞
n→∞
f ( A)
n
Esta ley basada en uno de los teoremas más importantes de la estadística: la desigualdad
de Chebyshev.
La probabilidad empírica es utilizada en estudios de problemas de física (constatación
empírica de teorías), por las compañías de seguros, y para la mayoría de experimentos que nos
e puede aplicar la probabilidad de Laplace. Si bien también se puede aplicar también a la teoría
de juegos, comprobando así si los sucesos son realmente equiprobables.
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
2
TEMA 63.Frecuencia y azar. Leyes de azar. Espacio probabilístico
Esta definición de probabilidad también admite críticas o limitaciones:
1. No queda claro cuando un experimento se realiza en las mismas condiciones
2. Sólo puede aplicarse a experimentos susceptibles de ser realizados las veces que se
desee.
Para problemas como el cálculo de la probabilidad de que mañana llueva o que gane un
equipo en partido de futbol no se puede aplicar tampoco esta probabilidad.
Probabilidad subjetiva: es el grado de creencia de mostrar que un suceso que puede ocurrir o no mediante un número comprendido entre 0 (suceso imposible) y 1 (suceso seguro). De
esta forma dependiendo del observador la probabilidad que le puede dar al mismo suceso es
totalmente distinta. Si bien estas probabilidades han de establecer unas reglas básicas, como
que la suma de la probabilidad de todos los sucesos incompatibles entre sí sea de 1.
Esta es la probabilidad utilizada cuando las dos anteriores no sean aplicables, bien por no
ser sucesos equiprobables o bien por no poderse repetir el experimento as veces que se desee.
Cualquiera de las tres formas de calcular la probabilidad debe cumplir un modelo teórico y
axiomático con el que se construye los espacios probabilísticos y que más tarde veremos.
3. Operaciones con sucesos. Espacio Muestral.
Definiremos previamente los siguientes conceptos:
Espacio muestral: es el conjunto formado por todos los posibles resultados de un experimento. Se representa por Ω. Por ejemplo en los dados Ω={1,2,3,4,5,6}
Suceso: es cada uno de los posibles subconjuntos del espacio muestral. Se denotan con letras mayúsculas. Ejemplo A=”impares”{1, 3, 5}
Sucesos elementales: son sucesos que no se pueden descomponer en sucesos más simples: A={1}.
Suceso imposible, el que no contiene ningún elemento de los sucesos de Ω., se denota
como ∅ (conjunto vacio) cumpliéndose que su probabilidad es cero.
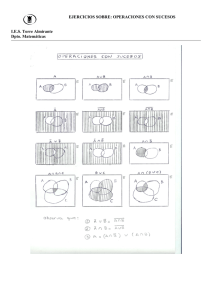
Operaciones con sucesos:
1. Unión de sucesos (A∪B) es el suceso formado por todos los elementos que pertenecen a uno de los dos conjuntos que unimos. Es decir A∪B={x∈Ω: x∈A o x∈B}.
2. Intersección de sucesos (A∩B) es el suceso formado por los sucesos elementales que
pertenecen a los dos conjuntos A y B. Es decir A∩B={x∈Ω: x∈A y x∈B}.
3. Diferencia de sucesos (A-B) es aquel formado por los elementos de A que no están en
B, es decir A-B={ x∈Ω: x∈A y x ∉ B }
ഥ o Ac) es el conjunto formado por los elementos de
4. Conjunto complementario de A (
Ω que no están en A. Es decir ܣҧ={x∈Ω: x ∉ A}
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
3
TEMA 63.Frecuencia y azar. Leyes de azar. Espacio probabilístico
La unión y la intersección pude generalizarse para una familia de conjuntos y no sólo
para dos como hemos visto en la definición:
UA
i
= {x ∈ Ω : x ∈ Ai para a lg ún i ∈ I }
i∈I
y
IA
i
= {x ∈ Ω : x ∈ Ai para a lg ún i ∈ I } .
i∈I
Partición: es un conjunto de conjuntos (A1, A2, …,An) que cumplen A1∪ A2, …∪An=Ω y
Ai∩Aj=∅.
Sucesos incompatibles: son aquellos que no tienen ningún elemento en común y por tanto
se cumple que su intersección es nula (A∩B=∅).
Propiedades de las operaciones con sucesos:
1.
2.
3.
4.
5.
6.
7.
8.
A ∪ ∅=A, A∩∅=∅ ∀A∈Ω
A ∪ Ω=Ω, A∩Ω=A ∀A∈Ω
A ∪ A=A, A∩A=A ∀A∈Ω
A ∪ B=B∪A y A∩B=B∩A
A∩(B∩C)=(A∩B)∪(A∩C)
A∪(B∪C)=(A∪B)∪C y A∩(B∩C)=(A∩B) ∩C
(Ac)c=A , (A∪B)c=Ac∩Bc , (A∩B)c=Ac∪Bc
A∩(B∪C)=(A∩B)∪(A∩C) y A∪(B∩C)=(A∪B)∩(A∪C)
9. Leyes de Morgan: ( A ∩ B ) = A ∪ B y ( A ∪ B ) = A ∩ B
Todas las propiedades se demuestran por lógica de conjuntos. Vamos una de ellas:
(A ∩ B) = A ∪ B
⊆ Veamos que ( A ∩ B ) ⊆ A ∪ B
Si x ∈ (A ∩ B) ⇒ x ∉ A ∩ B ⇒ x ∉ A ∨ x ∉ B ⇒ x ∈ A ∨ x ∈ B ⇒ x ∈ ( A ∪ B )
⊇ Veamos que ( A ∩ B ) ⊇ A ∪ B
Si x ∈ ( A ∪ B) ⇒ x ∈ A ∨ x ∈ B ⇒ x ∉ A ∨ x ∉ B ⇒ x ∉ ( A ∩ B) ⇒ x ∈ ( A ∩ B)
4. σ-álgebras de sucesos. Espacio probabilístico.
En este aparatado vamos a definir las condiciones que tienen que cumplir los conjuntos
sobre los que podemos aplicar la probabilidad. Sea Ω el conjunto de elementos y la potencia
de Ω, P(Ω), formada por todos los posibles subconjunto que se pueden hacer con los elementos de Ω.
Para que S⊆P(Ω) pueda ser una Ω-álgebra (de Boole) o espacio probabilístico ha de cumplir las siguientes condiciones:
1) Ω∈ S
2) Si A∈S Ac∈S
3) { An }∞n =1 ∈ S ⇒
∞
UA
n
∈S
n =1
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
4
TEMA 63.Frecuencia y azar. Leyes de azar. Espacio probabilístico
Propiedades que se deducen de la definición:
P1. : Si S es una Ω-álgebra se cumple que ∅∈S, pues ∅=Ωc
P2.: Si C es una Ω-álgebra y A,B∈S entonces A∩B, A-B, B-A∈S. Demostración:
A∩B=(AC∪BC)C
,
A-B=A∩BC,
B-A=B∩AC
Definición: Un espacio de probabilidad es una terna (Ω,S,℘) donde:
Ω es el espacio muestral, formado por todos los resultados posibles de la observación de un fenómeno aleatorio.
ii)
S es el conjunto de todos los sucesos y tiene estructura de σ-álgebra
iii)
℘ es la función de probabilidad que refleja la regularidad estadística del experimento; es una función real definida sobre C, ℘: S → ℝ, que satisface los siguientes axiomas:
1) ℘(A)≥0, ∀A∈C
i)
2) ℘(Ω)=1
∞ ∞
3) ℘ U An = ∑℘( An ), ∀{ An }n≥1 , An colección de sucesos de C incompatibles dos a
n =1 n =1
dos (Ai∩Aj=∅, ∀ i≠j)
A partir de las restricciones establecidas para Ω y C en la definición de espacio de probabilidad y de los axiomas 1), 2) y 3) se construye la teoría del cálculo de probabilidades.
Propiedades que se desprenden de la definición de (Ω,S,℘):
1) P(∅)=0 . Dem: se cumple ∅∪Ω=Ω p(∅∪Ω)=p(∅)+p(Ω)=p(Ω) p(∅)=0
2) P(AC)=1-p(A). Dem: se cumple A∪AC=Ω p(A∪AC)=p(A)+p(AC)=p(Ω)=1 p(AC)=1-p(A)
Ejemplos:
1) Lanzamiento de dados: Ω={1,2,3,4,5,6}, S=P(Ω) y definimos la función de probabilidad
℘: S ℝ
A p(A)=
cardinal ( A)
6
Si por ejemplo A={1,2} se cumple p(A)=2/6=1/3
2) Ω=[0, 2]x[0,2] (cuadrado en ℝ2 de tamaño 2) y S=P(Ω) y la función de probabilidad:
℘: S ℝ
A p(A)=
area ( A)
4
Si por ejemplo A=circulo radio unidad se cumple p(A)=π/4
En la mayoría de los casos cuando Ω es finito y numerable para definir un espacio probabilístico basta con asignar probabilidades positivas a los sucesos elementales de manera que la
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
5
TEMA 63.Frecuencia y azar. Leyes de azar. Espacio probabilístico
suma de todos ellos sumen 1, y definiendo la probabilidad de A, p(A), como
p(A)=card(A)/card(Ω) que es equivalente a Laplace:
1) Ω={u1, u2,…,un} y S=p(Ω)
2) p(ui)≥0:
n
∑
p (u i ) = 1
i =1
3) p(A)=
∑ p(u ) = 1
i
ui ∈ A
5. Propiedades del espacio probabilístico.
En el apartado anterior hemos visto alguna probabilidad de las propiedades más importantes del espacio probabilístico. Veamos ahora alguna más:
P1: p(∅)=0
P2: p(AC)=1-p(A)
P3: Si A,B∈Ω / A⊂B se cumple p(B-A)=p(B)-p(A∩B)
Dem: se cumple B=(A∩B)∪(B-A) y como (A∩B)∩(B-A)=∅ p(B)=p(A∩B))+p(B-A)
P4: Si A,B∈Ω y A⊂B p(A)≤p(B).
Dem: B=A∪(B-A), luego p(B)=p(A)+p(B-A) p(B)≥p(A)
P5: ∀A∈Ω se cumple p(A)≤1.
Dem: A⊂Ω, luego por P4 se cumple p(A)≤p(Ω)=1
P6: ∀A,B∈Ω se cumple p(A∪B)=p(A)+p(B)-p(A∩B)
Dem: por P2 A∪B=A∪(B-A) p(A∪B)=p(A)+p(B-A)=p(A)+p(B)-p(A∩B)
P7: ∀A1, A2,…,An∈Ω se cumple
n
p(A1∪A2…∪An)=
∑ p( A ) − ∑ p(A ∩ A ) + ∑ p( A ∩ A
i
i =1
i
j
i< j
i
j
∩ Ak ) + ...(−1) n p( A1 ∩... ∩ An )
i< j <k
Dem: Demostración por inducción del número de sucesos:
n=1 p(A1∪A2)=p(A1)+p(A2)-p(A1∩A2) (ya demostrado)
hip de inducción: n-1 p(A1…∪An-1)=
n−1
n−1
i =1
i< j
∑ p( Ai ) − ∑ p( Ai ∩ Aj ) +...(−1) n−1 p( A1..∩ An−1 )
Para n: p(A1∪A2…∪An)= p((A1…∪An-1)∪An)= p(A1∪A2…∪An-1)+p(An)- p(A1…∪An-1)∩An )=
=
n−1
n−1
i =1
i< j
∑ p( Ai ) − ∑ p( Ai ∩ Aj ) +...(−1) n−1 p( A1..∩ An−1 ) + p( An ) - p((A1∩An)…∪(An-1∩An ))=
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
6
TEMA 63.Frecuencia y azar. Leyes de azar. Espacio probabilístico
n
n−1
i =1
i< j
= ∑ p( Ai ) − ∑ p( Ai ∩ Aj ) + ...(−1)
n−1
=
n−1
∑ p( A ) − ∑ p( A ∩ A ) +...(−1)
i
i =1
i
j
n−1
n−1
p( A1 ..∩ An−1 ) − ∑ p( Ai ∩ An ) − ∑ p( Ai ∩ Aj ∩ An ) −...
i< j
i
n−1
n−1
p( A1 ..∩ An−1 ) .
i< j
6. Espacio de probabilidad de Laplace
Veremos en este apartado como la probabilidad clásica o de Laplace es un espacio probabilístico, es decir que cumplen los requisitos vistos en el aparatado 4.
Veamos como definiremos el espacio aleatorio de Laplace:
-
-
-
Sea un suceso considerado aleatorio donde Ω=”conjunto de todos los posibles sucesos
independientes que pueden ocurrir”. Ejemplo Ω=”1,2,3,4,5,6” si el suceso es lanzar un
dado.
Por otro lado definimos como S al conjunto de todos los subconjuntos de los elementos de Ω, de tal forma que tiene estructura de σ-algebra.
La aplicación probabilidad, p, asigna a cada suceso A el valor: p ( A ) =
card ( A )
card ( Ω )
Las dos primeras condiciones de espacio probabilístico ( I Ω es el espacio muestral, formado por todos los resultados posibles de la observación de un fenómeno aleatorio y II S es el
conjunto de todos los sucesos y tiene estructura de σ-álgebra) se cumplen por construcción.
Veremos la relativa a la aplicación probabilidad:
1) ℘(A)≥0, ∀A∈C Por definición de cardinal, se cumple que card(A), card(Ω)≥0
2) ℘(Ω)=1 ℘(Ω)=
card (Ω)
=1
card (Ω)
∞ ∞
3) ℘ U An = ∑℘( An ), ∀{ An }n≥1 , An colección de sucesos de C incompatibles dos a
n =1 n =1
dos (Ai∩Aj=∅, ∀ i≠j) Si los sucesos son incompatibles no tendrán sucesos en
∞
común, por tanto se cumple que card(
∞
U A ) = ∑ card ( A ) , por tanto se cumple
n
n=
n
n =1
∞
∞
que p U An =
n=
∑ card ( A )
n
n =1
card (Ω)
∞
card ( An ) ∞
= ∑ p( An )
n =1 card (Ω)
n =1
=∑
7. Espacio de probabilidad empírica o de grandes números.
Al igual que hemos comprobado que la probabilidad clásica cumple la definición de espacio probabilístico, veremos ahora la probabilidad empírica definida con anterioridad y con los
siguientes requisitos:
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
7
TEMA 63.Frecuencia y azar. Leyes de azar. Espacio probabilístico
-
-
-
Sea un suceso considerado aleatorio donde Ω=”conjunto de todos los posibles sucesos
independientes que pueden ocurrir”. Ejemplo Ω=”1,2,3,4,5,6” si el suceso es lanzar un
dado.
Por otro lado definimos como S al conjunto de todos los subconjuntos de los elementos de Ω, de tal forma que tiene estructura de σ-algebra.
La aplicación probabilidad, p, asigna a cada suceso A el valor: p ( A ) =
fA
. Donde fA
n
es el número de veces que ocurre el suceso A de las n veces que se repite (teóricamente este valor n tiende a infinito).
Las dos primeras condiciones de espacio probabilístico ( I Ω es el espacio muestral, formado por todos los resultados posibles de la observación de un fenómeno aleatorio y II S es el
conjunto de todos los sucesos y tiene estructura de σ-álgebra) se cumplen por construcción.
Veremos la relativa a la aplicación probabilidad:
1) ℘(A)≥0, ∀A∈C Por definición de fA y n, se cumple que fA y n≥0.
2) ℘(Ω)=1 ℘(Ω)=
fΩ n
= =1
n n
∞ ∞
3) ℘ U An = ∑℘( An ), ∀{ An }n≥1 , An colección de sucesos de C incompatibles dos a
n =1 n =1
dos (Ai∩Aj=∅, ∀ i≠j) Si los sucesos son incompatibles no tendrán sucesos en
∞
común, por tanto se cumple que f( f ∞
U An
n=
= ∑ f An , por tanto se cumple que
n =1
∞
∞
p U An =
n=
∑f
n =1
n
An
∞
=∑
n =1
f AN
n
∞
= ∑ p ( An )
n =1
8. Conclusiones.
Hemos visto en el desarrollo del tema el proceso de matematización de un aspecto de la
realidad altamente complejo. Para obtener de un fenómeno aleatorio un concepto que va a
pertenecer a la abstracta Matemática, hemos localizado sus aspectos característicos y los
hemos convertido en Álgebra abstracta. A partir de este momento, nos centramos exclusivamente en los aspectos abstraídos que se regirán exclusivamente por las leyes algebraicas, y se
desarrollarán en fórmulas que se aplicarán luego a la realidad, de nuevo.
La probabilidad se imparte en secundaria desde 2º curso de secundaria hasta 2º de bachillerato.
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
8