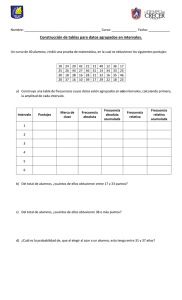
INSTITUCIÓN EDUCATIVA RAFAEL URIBE URIBE TRIGONOMETRÍA - GRADO 10 GUÍA NO. 5 Docente: CARLOS ALBERTO LONDOÑO GUATIVA - Celular: 3147234861 FECHA E_mail: [email protected] GEOMETRÍA- punto medio de un segmento – inclinación y Tema: TIEMPO pendiente ESPERADO ESTADÍSTICA- Datos agrupados-Representaciones graficas-medidas de posición INTENSIDAD HORARIA 4 HORAS SEMANALES 1/08/2021 30/08/2021 20- HORAS GEOMÉTRÍA INSTRUCCIONES: La primera semana es para trabajar los temas de geometría analítica y punto medio, se desarrollarán las actividades básicas y la actividad de práctica 1. En la segunda semana se trabajará con el tema de pendiente, se desarrollará la actividad de práctica 2 y la actividad de aplicación. Desempeño: - Reconoce las ecuaciones de la recta Eje Temático: - Punto medio de un segmento - Inclinación y pendiente DESCRIPCIÓN DE LA GEOMETRÍA ANALÍTICA En el desarrollo de las matemáticas es muy usual encontrarse con muchos problemas, algunos muy diferentes entre ellos; es muy habitual, que en algunos casos, debamos recurrir a diferentes ramas de las matemáticas para dar solución a dichas situaciones. Incógnitas cómo la de ubicar la posición de una persona a nivel mundial demandan conocimiento geométrico y algebraico ACTIVIDADES BASICAS Leer la siguiente situación Olga y Pipe ven una película de acción, en donde el malo delata su ubicación al haber realizado una llamada, esto no termina de convencer a Pipe quien cree que es imposible que esto ocurra en la vida real, Olga propone a Pipe que salgan de esa inquietud preguntándole a su amigo Buksy, quien les explica que este tipo de acontecimientos son posibles y todo ello gracias a las matemáticas y los sistemas coordenados de posición. Buksy explica que, por ejemplo, para para determinar la posición de una persona dentro de una fila, basta con saber su turno, y que este tipo de eventos pueden ser representados sobre una recta numérica, a este sistema de posición se le conoce como sistema coordenado unidimensional; pero también se conocen otros sistemas coordenados como lo es el bidimensional, el cual consiste en una posición que se determina por qué tan arriba o tan abajo se encuentra un objeto con respecto a una recta horizontal y que tan a la izquierda o a la derecha se encuentra de una recta vertical, este último sistema es el que utiliza los GPS para encontrar las personas a nivel mundial; el funcionamiento del sistema GPS se basa en procesos geométricos y algebraicos para determinar las coordenadas de la posición del objeto y es así como se puede encontrar personas como el ladrón en la película de vieron Olga y Pipe 1. ¿En qué se diferencian el sistema coordenado unidimensional con el sistema coordenado bidimensional? Escriba un ejemplo de la vida real para cada sistema, diferente del que se menciona en el texto 2. Escriba cuál de los siguientes problemas se desarrollan únicamente con Geometría y Álgebra, como también cuales requieren del uso de las dos: a. Dado un triángulo determinar si es escaleno b. Calcular el valor de X si 32 + 8x – 21 = 0 c. Hallar el punto de intersección entre dos rectas d. Determinar si un polígono es un rectángulo Elementos de la geometría analítica Olga se encuentra algo pensativa al conocer a la geometría analítica, aunque ya sabemos que la Geometría Analítica estudia aquellos problemas en los que es necesario utilizar Geometría y Algebra para ser solucionados, no conocemos cuales son los objetos que estudia, sin embargo para dar respuesta a la inquietud de Olga, Pipe nos propone el siguiente problema. 3. Con lo que nos propone Pipe escribe si cada una de las siguientes imágenes son o no son lugares geométricos 4. Consulte y escriba que es un lugar geométrico. Dibuje 3 lugares geométricos diferentes a los vistos anteriormente. PUNTO MEDIO DE UN SEGMENTO Se desea saber las coordenadas de un aeropuerto que queda exactamente en la mitad del camino que recorre un avión que parte desde la coordenada (500,300) para llegar a la coordenada (-400,-200). Para solucionar este problema lo primero que se debe hacer es una gráfica de la situación. El aeropuerto que se encuentra en la mitad del camino, se ubica en las coordenadas (50,50) Es posible determinar el punto medio entre dos puntos. En la siguiente figura se muestra el segmento que une los puntos P1(X1, Y1) y P2(X2, Y2) del plano. Las coordenadas del punto medio M(x, y) vienen dadas por la semisuma de las coordenadas de los extremos. Fórmula de Punto Medio En el problema del aeropuerto que queda en la mitad del camino, se puede saber las coordenadas empleando la fórmula del punto medio, así: La primera coordenada es (500,300) y la segunda coordenada es (-400, -200), aplicando la fórmula 𝒙𝟏 + 𝒙𝟐 𝒚𝟏 + 𝒚𝟐 𝑴= ( , ) 𝟐 𝟐 𝑴= ( 𝟓𝟎𝟎 + (−𝟒𝟎𝟎) 𝟑𝟎𝟎 + (−𝟐𝟎𝟎) , ) 𝟐 𝟐 𝑴= ( 𝟏𝟎𝟎 𝟏𝟎𝟎 , ) 𝟐 𝟐 𝑴 = (𝟓𝟎, 𝟓𝟎) Ejemplo Hallar las coordenadas del punto medio M del segmento PR, si se sabe que P (-6, -6) y R (10, 2) Se reemplazan los valores de cada coordenada en la fórmula de punto medio 𝑴= ( 𝒙𝟏 + 𝒙𝟐 𝒚𝟏 + 𝒚𝟐 , ) 𝟐 𝟐 −𝟔 + 𝟏𝟎 −𝟔 + 𝟐 𝑴= ( , ) 𝟐 𝟐 𝑴= ( 𝟒 −𝟒 , ) 𝟐 𝟐 M = (2, -2) ACTIVIDADES DE PRÁCTICA 1 1. Calcule las coordenadas de los puntos medios de estas rutas de avión, empleando la fórmula del punto medio. a. (-100,-400), (300,700) b. (100,500), (200,0) 2. Teniendo en cuenta el triángulo ABC, halle los puntos medios de los lados del triángulo, empleando la fórmula de Punto Medio, luego ubíquelos en el plano y únalos. INCLINACION Y PENDIENTE Al representar una recta en el plano cartesiano se pueden dar varios casos, teniendo en cuenta el ángulo de inclinación α y la pendiente m. Observe la recta L que se representa en cada uno de los planos. La pendiente de una recta indica la variación entre los incrementos en el eje y respecto de los incrementos en el eje x. Si se toman dos puntos (x1, y1) y (x2, y2) pertenecientes a una recta, la pendiente m es la razón de cambio entre el desplazamiento vertical respecto del desplazamiento horizontal y está dada por: 𝑷𝒆𝒏𝒅𝒊𝒆𝒏𝒕𝒆 (𝒎) = 𝑑𝑒𝑠𝑝𝑙𝑎𝑧𝑎𝑚𝑖𝑒𝑛𝑡𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙 𝑑𝑒𝑠𝑝𝑙𝑎𝑧𝑎𝑚𝑖𝑒𝑛𝑡𝑜 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙 𝒎= 𝑌2 − 𝑌1 𝑋2 − 𝑋1 Además, para cualquier par de puntos se forma un triángulo rectángulo, donde la razón entre los catetos está relacionada con el ángulo de inclinación de la recta 𝒎= 𝑌2 − 𝑌1 = 𝑻𝒂𝒏 𝜶 𝑋2 − 𝑋1 Es decir que m = Tan α, por lo tanto para hallar el ángulo de inclinación se hace lo siguiente: m = Tan α, entonces Tan -1 m = α Se despeja el ángulo α, pasando la Tan al lado de m Ejemplo: Determinar la pendiente y el ángulo de inclinación de la recta AB con respecto al eje x Para determinar la pendiente de AB, se debe escribir las coordenadas (x, y) de los puntos A y B. Las coordenadas de A (0, 4) y de B (2, 1), empleamos la fórmula de la pendiente y reemplazamos los valores de cada coordenada: 𝒎= La pendiente es m = −𝟑 𝟐 𝒀𝟐 − 𝒀𝟏 1−4 −3 = = 𝑿𝟐 − 𝑿𝟏 2−0 2 , como es negativa, la recta es decreciente. El 3 indica las unidades del desplazamiento vertical y el 2 las unidades del desplazamiento horizontal. Ahora con la pendiente calculamos el ángulo de inclinación α, recordemos que: m = Tan α, entonces Tan -1 m = α Tan -1 −𝟑 𝟐 = α − 56° = α Se despeja el ángulo α, al pasar Tan al lado de la pendiente m, queda Tan -1 Se digita en la calculadora (shift Tan), para que salga Tan -1 y luego el (-3 ÷ 2) y aparece el valor del ángulo α α es igual a -56° ACTIVIDADES DE PRÁCTICA 2 1. Determine la pendiente de la recta que pasa por los puntos señalados y su ángulo de inclinación respecto al eje x a. b. c. ACTIVIDADES DE APLICACIÓN Si tiene internet en su casa, ingrese a los siguientes enlaces en los cuales podrá ver ejercicios relacionados con punto medio y pendiente. https://www.superprof.es/apuntes/escolar/matematicas/analitica/vectores/ejercicios-interactivos-de-lascoordenadas-del-punto-medio-y-del-baricentro.html https://matemovil.com/pendiente-de-una-recta-ejercicios-resueltos/ 1. Dados los puntos P (-2, 4) y Q (3, -1) las coordenadas del punto medio de PQ son: 1 3 a. ( 2 , 2 ) −1 − 3 , 2 ) 2 c. ( b. (1, 3) d. (-1, -3) 2. En la figura se presenta un mapa de la vista aérea de las calles de una parte de una ciudad. Se muestran tres puntos A, B y C; y la medida de dos segmentos sobre el mapa. Cada uno de los cuadriláteros ilustrados corresponde a un cuadrado. Una representación de los posibles caminos entre dos puntos X y Y en la ciudad se da al establecer el número de posibilidades entre ellos. Por ejemplo: si entre los puntos X y Y hay tres caminos posibles se escribe X (3) Y. La representación de los posibles caminos A a B de longitud igual a 25 cm, pasando por C, es: a. A (1) C (1) B c. A (4) C (2) B b. A (3) C (2) B d. A (2) C (1) B ESTADISTÍCA INSTRUCCIONES: La primera semana es para trabajar el tema de tabla de frecuencia para datos agrupados, se desarrollarán la actividad de práctica 1. En la segunda semana se trabajará con el tema de medidas de posición, se desarrollará la actividad de práctica 2 y en la tercera semana se trabajará con la actividad de aplicación y nivelaciones. Desempeño: - Construye tablas de frecuencia para variables continuas y las representa con gráficas Aprendizaje: -Datos agrupados - Representaciones gráficas - Medidas de posición TABLAS DE FRECUENCIA PARA DATOS AGRUPADOS Cómo construir una tabla de frecuencias con datos agrupados en intervalos. Si tenemos un número muy grande de datos, éstos se agrupan en intervalos, para no tener que realizar tablas muy largas con muchos datos diferentes. También se agrupan en intervalos cuando las variables son continuas. En estos casos se realiza una tabla de frecuencias con datos agrupados. Los datos se agrupan en intervalos, llamados clases y es a estos intervalos que se les asignan sus frecuencias correspondientes. Sobre las clases, debes conocer los siguientes conceptos: Límites de clase: Cada intervalo tiene un límite inferior, que pertenece a ese intervalo (cerrado por la izquierda con un corchete) y un límite superior que no pertenece (abierto por la derecha) Amplitud de clase: La amplitud es la diferencia entre el límite superior e inferior y debe ser la misma para cada intervalo Marca de clase: Es el punto medio de cada intervalo y es el valor que se utiliza para calcular otras medidas Vamos a ver un ejemplo de realizar una tabla de frecuencias con datos agrupados en intervalos: EJEMPLO Se toma una muestra de peces de una cierta especie y se miden sus longitudes en centímetros, cuyos resultados son: 5.0, 6.2, 7.4, 7.5, 6.4, 6.7, 5.9, 6.1, 7.1, 6.8, 7.3, 5.7, 6.8, 7.1, 7.2, 5.1, 7.2, 7.3, 5.5, 7.3, 7.4, 6.8, 6.6, 5.5 Obtener la tabla de frecuencias absolutas, relativas, acumuladas, porcentaje y marca de clase. La tabla de frecuencias tendrá las siguientes 7 columnas: Intervalos Frecuencia absoluta (fi) Frecuencia absoluta acumulada (Fi) Frecuencia relativa (hi) Frecuencia relativa acumulada (Hi) Frecuencia Porcentual (%) Marca de Clase (MC) Para rellenar la primera columna, tenemos que determinar el número de intervalos y la amplitud de los mismos. Para ello se identifica el valor más pequeño y el valor más grande, que en este caso son 5.0 y 7.5 respectivamente, y el total de los datos, que son 24 peces, con esos valores se realizan los siguientes procedimientos: 1. Rango = Dato Mayor – dato menor Rango = 7.5 – 5 = 2.5 2. Número de intervalos = √𝑛 n, total de los datos Núm. Intervalos = √𝟐𝟒 = 4,8 se aproxima para trabajar con un número entero 5 3. Amplitud del intervalo = Amplitud Intervalo = 𝑅𝑎𝑛𝑔𝑜 𝟐.𝟓 𝟓 √𝑛 = 0.5 Ahora el número de intervalos son 5 y la amplitud es 0.5 Nos quedan los siguientes intervalos: Dejamos la última fila para el total. Para completar la columna de frecuencia absoluta, tenemos que ir contando los valores que pertenecen a cada intervalo. Si por ejemplo tuviéramos el valor 5,5, pertenecería al segundo intervalo y no al primero, ya que el primer intervalo es abierto hasta 5,5, es decir, el 5,5 no está incluido y el segundo intervalo comienza a partir de 5,5, que sí está incluido, ya que el intervalo es cerrado por la izquierda. Después de contar nos queda de la siguiente manera: Para completar la columna de la frecuencia absoluta acumulada de cada intervalo lo hacemos igual que en el caso anterior: en la primera fila, la frecuencia absoluta acumulada coincide con la frecuencia absoluta y para el resto de filas, la frecuencia absoluta acumulada la obtenemos sumando la frecuencia absoluta acumulada del dato anterior (del dato de arriba) más su frecuencia acumulada (dato de su izquierda). Nos queda: La frecuencia relativa la calculamos dividiendo cada frecuencia absoluta, entre el número total de elementos: Por ejemplo, para el tercer intervalo, la frecuencia relativa es: Lo hacemos igual para el resto de intervalos y en la última fila, colocamos la suma de las frecuencias relativas: La frecuencia relativa acumulada del primer dato es igual que su frecuencia relativa y para los datos siguientes es igual a su frecuencia relativa más la frecuencia relativa del dato anterior (del dato de arriba): Intervalos Frecuencia absoluta fi Frecuencia Acumulada Fi Frecuencia relativa hi Frecuencia Relativa Acumulada Hi [ 5.0 – 5.5) 2 2 0,083 0,083 [ 5.5 – 6.0) 4 6 0,16 0,243 [ 6.0 – 6.5 ) 3 9 0,125 0,368 [ 6.5 – 7.0 ) 5 14 0,208 0.576 [ 7.0 – 7.5 ] 10 24 0,416 0,99 Total 24 Porcentaje % Marca de Clase MC 0,99 El porcentaje se calcula multiplicando la frecuencia relativa por 100 y la Marca de clase se calcula, sumando los valores de cada intervalo y el resultado se divide entre dos.(es un promedio), es decir: En el intervalo 1, los valores son 5,0 y 5,5, se suman y se dividen entre dos. MC = 5.0 + 5.5 2 = 10.5 2 = 5,25 Intervalos Frecuencia absoluta fi Frecuencia Acumulada Fi Frecuencia relativa hi Frecuencia Relativa Acumulada Hi Porcentaje % Marca de Clase MC [ 5.0 – 5.5) 2 2 0,083 0,083 8,3 % 5,25 [ 5.5 – 6.0) 4 6 0,16 0,243 16 % 5,75 [ 6.0 – 6.5 ) 3 9 0,125 0,368 12,5 % 6,25 [ 6.5 – 7.0 ) 5 14 0,208 0.576 20,8 % 6,75 [ 7.0 – 7.5 ] 10 24 0,416 0,99 41,6 % 7,25 Total 24 0,99 99 % REPRESENTACIONES GRÁFICAS Los gráficos más representativos para las variables cuantitativas continuas representadas en tablas de frecuencias son los histogramas, el polígono de frecuencias y la ojiva. ¿Qué es un histograma? Un histograma es la representación gráfica en forma de barras, que simboliza la distribución de un conjunto de datos. Sirven para obtener una "primera vista" general, o panorama, de la distribución de la población, o de la muestra, respecto a una característica, cuantitativa y continua. En un histograma el eje de las (o abscisas) se ubican los intervalos, en los que agrupamos los datos y son las bases de los rectángulos. Por otro lado, en el eje de las las barras. (u ordenadas) se ubica la frecuencia absoluta, que determina la altura de Teniendo en cuenta el ejemplo de los peces, vamos a representar esa tabla de frecuencias en un histograma. Polígono de frecuencias ¿Qué es un polígono de frecuencias? Un polígono de frecuencias es una herramienta gráfica que se emplea a partir de un histograma de frecuencia. Para ello, se unen con una línea los distintos puntos medios de las columnas del histograma, sin dejar espacio entre una y otra, logrando así una forma geométrica o polígono. Para construir un polígono de frecuencias, se ubica en el eje horizontal X (abscisa) la Marca de Clase de cada intervalo. Luego, en el eje vertical Y (ordenada) se ubican las frecuencias obtenidas en la tabla. Utilizando el ejemplo de los peces, construimos el polígono de frecuencia. Peso de peces Frecuencia absoluta 12 10 8 6 4 2 0 5.25 5.75 6.25 6.75 7.25 Marca de clase en kg OJIVA ¿Qué es una ojiva? Una gráfica de ojiva es aquella que representa frecuencias acumuladas. Se calcula sumando las frecuencias de cada clase y las clases previas. Su aplicación se concreta a responder preguntas como: ¿Qué proporción acumulada le corresponde a este dato?, ¿Qué dato corresponde a esta proporción acumulada? Ahora, construye la gráfica de ojiva, en el eje en eje X (abscisa) las marcas de cada clase y en el eje Y (ordenada) se grafican las frecuencias acumuladas. Frecuencia absoluta Acumulada Peso de peces 30 25 20 15 10 5 0 5,25 5,75 6,25 6,75 7,25 Marca de Clase en Kg ACTIVIDAD DE PRÁCTICA 1 1. Un examen presentado por 30 alumnos se calificó con puntos de 1 a 50. Los resultados fueron los siguientes: 13, 21, 36, 15, 38, 27, 34, 41, 10, 36, 48, 37, 36, 18, 19, 31, 24, 30, 45, 29, 11, 28, 32, 26, 42, 16, 12, 9, 7, 20 a. Elaborar la tabla de frecuencias para datos agrupados b. ¿Cuál es la mayor frecuencia relativa y el menor porcentaje, a qué datos corresponden? c. Elaborar el histograma 2. En el colegio se mantiene el registro de la estatura en centímetros de los estudiantes de 10°. Los datos son: 142, 165, 146, 178, 157, 181, 180, 170, 152, 158, 147, 176, 165, 170, 153, 175, 165, 169, 149, 153, 178, 150, 162, 173, 160, 149, 156, 145, 150, 182. a. b. c. d. Elaborar la tabla de frecuencias para datos agrupados ¿Cuál es la menor frecuencia relativa y el mayor porcentaje, a qué datos corresponden? Elaborar el polígono de frecuencias Elaborar la ojiva MEDIDAS DE POSICION Las medidas de posición como los cuartiles, deciles y percentiles dividen a una distribución ordenada en partes iguales. Para calcular las medidas de posición, se deben aplicar las fórmulas correspondientes a cada una de ellas. LOS CUARTILES Los cuartiles (Qk): son los tres valores de la variable de una distribución que la dividen en cuatro partes iguales, es decir, al 25%, 50% y 75%. Para calcular el valor de uno de los cuatro Cuartiles, se utilizan las siguientes fórmulas: En primer lugar buscamos la clase donde se encuentra frecuencias acumuladas. Qk = Li + 𝑵.𝒌 𝟒 − 𝑭𝒊−𝟏 𝒇𝒊 * ai k = 1, 2, 3 Donde: Li : Es el límite inferior del intervalo donde se encuentra el cuartil ai : Es la amplitud del intervalo. fi : Es la frecuencia absoluta del intervalo donde se encuentra el cuartil Fi-1: Es la frecuencia Acumulada anterior al intervalo donde se encuentra el cuartil N: es el total de datos. , en la tabla de las Ejemplo de ejercicio de cuartiles Calcular los cuartiles de la distribución de la tabla: Cálculo del primer cuartil Buscamos el intervalo donde se encuentra el primer cuartil, multiplicando por 4. 𝑁. 𝐾 65 ∗ 1 = = 16.25 4 4 Buscamos en la columna de las frecuencias acumuladas La clase de por y dividiendo el intervalo que contiene a . es: Aplicaremos la fórmula para el cálculo de cuartiles para datos agrupados, extrayendo los siguientes datos: El 25% de los datos está por debajo de 68,25 y el 75% están por encima Cálculo del segundo cuartil Buscamos el intervalo donde se encuentra el segundo cuartil, multiplicando por . 𝑁. 𝐾 4 = 65 ∗ 2 4 y dividiendo = 32.5 Buscamos en la columna de las frecuencias acumuladas La clase de por el intervalo que contiene a . es: Aplicaremos la fórmula para el cálculo de cuartiles para datos agrupados, extrayendo los siguientes datos: El 50% de los datos está por debajo de 79,06 y el 50% está por encima LOS DECILES Los deciles (Dk) corresponden a los 9 valores que dividen a estos en 10 partes iguales, es decir, al 10%, al 20%... y al 90%. Los Deciles se designan por D1, D2,..., D9. Para calcular los deciles se utiliza la siguiente fórmula: Dk = Li + 𝑁∗𝑘 10 −𝐹𝑖−1 𝑓𝑖 * ai k = 1, 2, 3, 4, 5, 6, 7, 8, 9 Donde: Li : Es el límite inferior del intervalo donde se encuentra el cuartil ai: Es la amplitud del intervalo. fi: Es la frecuencia absoluta del intervalo donde se encuentra el cuartil. Fn-1: Es la frecuencia acumulada anterior al intervalo donde se encuentra el cuartil. N: es el total de datos. Ejemplo de ejercicio de deciles Calcular los deciles de la distribución de la tabla Cálculo del primer decil Buscamos el intervalo donde se encuentra el primer decil, multiplicando por 𝑁. 𝐾 10 = 65 ∗ 1 10 y dividiendo = 6.5 Buscamos en la columna de las frecuencias acumuladas La clase de por el intervalo que contiene a es: Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos: El 10% de los datos se ubican por debajo de 58,12 y el 90% por encima LOS PERCENTILES Los percentiles (Pk) son los noventa y nueve valores de la variable de una distribución que la dividen en cien partes iguales, es decir, al 1%, al 2%... y al 99% de los datos. Los percentiles se designan por P1, P2,... P99. Luego, Para calcular el percentil Pk se utiliza la siguiente fórmula: Pk = Li + 𝑁∗𝑘 100 − 𝐹𝑖−1 𝑓𝑖 * ai Donde: Li : Es el límite inferior del intervalo donde se encuentra el k% de los datos. ai : Es la amplitud del intervalo. fi : Es la frecuencia absoluta del intervalo donde se encuentra el k% de los datos. Fi-1: Es la frecuencia acumulada anterior al intervalo donde se encuentra el k% de los datos. N: es el total de datos. Ejemplo de ejercicio de percentiles Calcular los percentiles de la distribución de la tabla Cálculo de los percentiles En primer lugar buscamos la clase donde se encuentra frecuencias acumuladas. , en la tabla de las Cálculo del percentil 35 Buscamos el intervalo donde se encuentra el percentil por 𝑁. 𝐾 100 = 65 ∗ 35 100 por y dividiendo = 22.75 Buscamos en la columna de las frecuencias acumuladas La clase de , multiplicando el intervalo que contiene a es: Aplicaremos la fórmula para el cálculo de percentiles para datos agrupados, extrayendo los siguientes datos: El 35% de los datos se ubica por debajo de 72,97 y el 65% por encima ACTIVIDAD DE PRACTICA 2 1. Complete la siguiente Tabla de frecuencias, la columna de Frecuencia Acumulada y responda las siguientes preguntas VARIABLE (Edades) [3-6) [6-9) [9-12) [12-15) [15-18) [18-21] Fi Fi a. Calcule e interprete los siguientes CUARTILES: Q1 ; Q2 b. Calcule e interprete los siguientes DECILES: D1; D7 c. Calcule e interprete los siguientes PERCENTILES: P28; P80 25 15 20 30 10 20 2. Complete la siguiente Tabla de frecuencias, la columna de Frecuencia Acumulada y responda las siguientes preguntas VARIABLE (Estaturas en cm) [150-155) [155-160) [160-165) [165-170) [170-175) [175-180] fi 24 6 30 12 8 10 Fi a. Calcule e interprete los siguientes CUARTILES: Q1 ; Q3 b. Calcule e interprete los siguientes DECILES: D2; D6 c. Calcule e interprete los siguientes PERCENTILES: P10; P66 ACTIVIDADES DE APLICACIÓN RESPONDA LAS PREGUNTAS 1 Y 2 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN Pedro y Juan viven en un apartamento y comparten el pago de los gastos. En octubre, el consumo de gas natural se facturó por $14.500, incluido el cargo fijo de $2.700, que es el mismo todos los meses. La gráfica muestra el consumo histórico en metros cúbicos de ese servicio. 1. Un hogar puede consumir máximo 20 metros cúbicos en un mes. ¿A qué porcentaje del consumo máximo posible corresponde el consumo de junio? A. 15% C. 75% B. 25% D. 100% 2. Para saber cuál es el costo promedio del consumo diario, se resta del cobro total de ese mes, el valor por cargo fijo, y luego se divide entre 30, que es el número de días que se utiliza para facturar un mes. ¿Cuál es el costo promedio aproximado, en pesos, del consumo diario de octubre? A. 90 C. 483 B. 393 D. 907