Examen Análisis de Datos: Regresión y Series de Tiempo
Anuncio
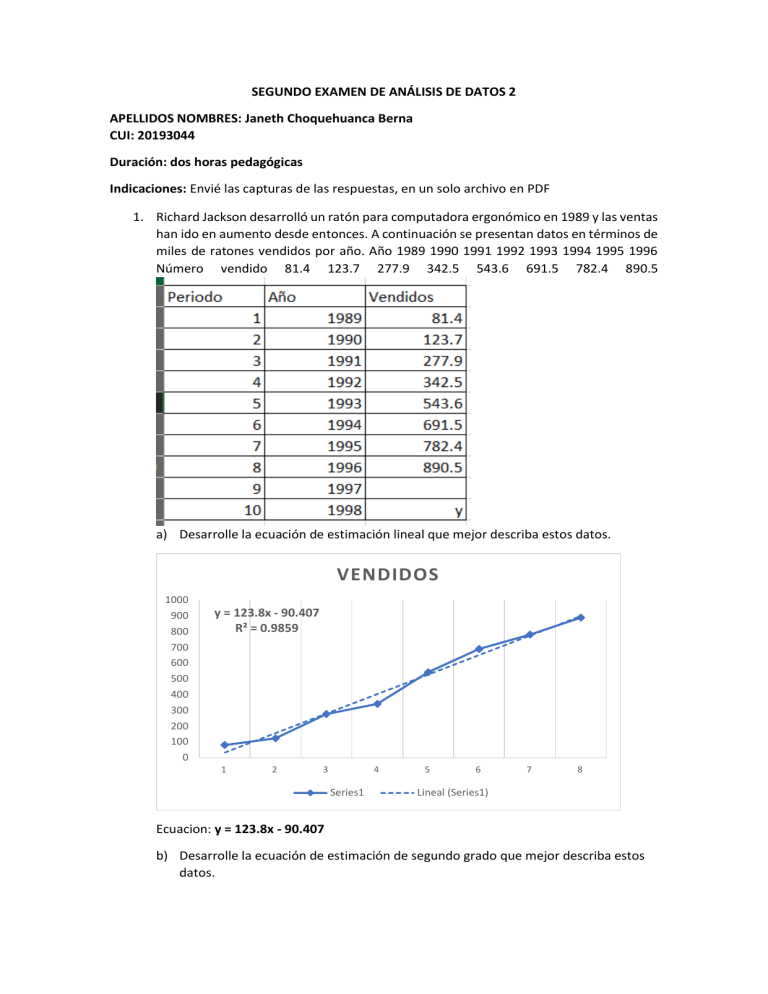
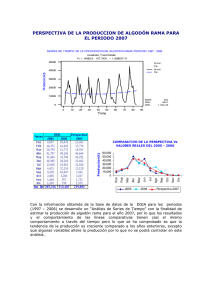
SEGUNDO EXAMEN DE ANÁLISIS DE DATOS 2 APELLIDOS NOMBRES: Janeth Choquehuanca Berna CUI: 20193044 Duración: dos horas pedagógicas Indicaciones: Envié las capturas de las respuestas, en un solo archivo en PDF 1. Richard Jackson desarrolló un ratón para computadora ergonómico en 1989 y las ventas han ido en aumento desde entonces. A continuación se presentan datos en términos de miles de ratones vendidos por año. Año 1989 1990 1991 1992 1993 1994 1995 1996 Número vendido 81.4 123.7 277.9 342.5 543.6 691.5 782.4 890.5 a) Desarrolle la ecuación de estimación lineal que mejor describa estos datos. VENDIDOS 1000 900 800 700 600 500 400 300 200 100 0 y = 123.8x - 90.407 R² = 0.9859 1 2 3 4 Series1 5 6 7 8 Lineal (Series1) Ecuacion: y = 123.8x - 90.407 b) Desarrolle la ecuación de estimación de segundo grado que mejor describa estos datos. VENDIDOS 1000 900 800 700 600 500 400 300 200 100 0 y = 2.2065x2 + 103.94x - 57.309 R² = 0.9872 1 2 3 4 Vendidos 5 6 7 8 Polinómica (Vendidos) Ecuacion: y = 2.2065x2 + 103.94x - 57.309 c) Estime el número de ratones que venderá en 1998 usando ambas ecuaciones. d) Si se supone que la tasa de crecimiento de las ventas de ratones decrecerá pronto con base en la oferta y la demanda, ¿qué modelo será un mejor pronosticador para su respuesta en c)? (6P) usaría en modelo de segundo grado , ya que se tiene mas vendidos con ese modelo. 2. Se tiene los siguientes resultados: (3p) SES Tendencia lineal MAPE 6.1313 MAPE 7.9624 MAD 3.1314 MAD 3.7056 MSD 21.2324 MSD 24.985 Pregunta: Interprete los resultados planteados. SES MAPE MAD MSD MAPE MAD MSD Tendencia lineal MAPE 7.9624 MAD 3.7056 MSD 24.985 6.1313 3.1314 21.2324 El pronostico está errado en un 6,13%; ya que; el MAPE nos expresa la exactitud como un porcentaje de error. Vemos que el MAD es 3.13 y es un valor pequeño, lo que significa que tenemos un mejor ajuste del modelo. Nos da un valor de 21.23, esto nos mide la exactitud de los valores ajustados en las series de tiempo. MAPE MAD MSD El pronostico de tendencia lineal está errado en un 7,96%; ya que; el MAPE nos expresa la exactitud como un porcentaje de error. Vemos que el MAD es 3.70 y es un valor pequeño, lo que significa que tenemos un mejor ajuste del modelo, pero el modelo SES se ajusta mejor, según el MAD. Nos da un valor de 24.98, esto nos mide la exactitud de los valores ajustados en las series de tiempo, en comparación con SES, tenemos un mayor valor, osea que ese modelo se ajusta mejor, pues tiene un MSD menor que el nuestro. En conclusión, el modelo SES se ajusta mejor, ya que, según las medidas de exactitud dadas, tenemos valores menores en dicho modelo. 3. En la siguiente tabla aparece el número de boletos para cine que vendió el Cinemid, en miles, durante el periodo de 1988 a 2010. Calcule el promedio móvil ponderado de cinco años con ponderación de 0.1, 0.1, 0.2, 0.3 y 0.3, respectivamente. Describa la tendencia de rendimiento. (6P) Año Boletos 1998 8.61 1999 8.14 2000 7.67 2001 6.59 2002 7.37 2003 6.88 2004 6.71 2005 6.61 2006 5.58 2007 5.87 2008 5.94 2009 5.49 2010 5.43 4. Se cuanta con la demanda de 12 meses, se desea que realice la suavización correspondiente, para alfa: 0.1, 0.3 y 0.7. Realice la gráfica y la interpretación del resultado. (5P) PERIODO DEMANDA 1 1800 2 1100 3 1800 4 1850 5 2900 6 1550 7 1350 8 1100 9 2000 10 2550 11 2150 12 2100