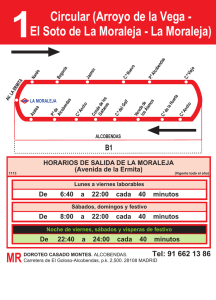
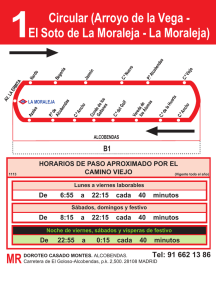
RESUMEN MATEMática
CUADERNO RESUMEN DE CONTENIDOS - PSU MATEMATICA
www.moraleja.cl
I. NÚMEROS
C
1. CONJUNTOS NUMÉRICOS
I
R
2 Números Naturales: N = { 1 , 2 , 3 , 4 , 5 , ... }
Q*
Q
Z
2 Números Cardinales: N0 = { 0 , 1 , 2 , 3 , 4 , 5 , ... }
N0
2 Números Enteros: Z = { ... , –2 , –1 , 0 , 1 , 2 , ... }
N
2 Números Racionales Q. Aquellos que se pueden expresar de la
forma a = k con a, b números enteros y b ≠ 0.
b
–4
Ejemplos: { 1 , 0,2 ,
, 2,31 , ... }
3
2 Números Irracionales Q*. Números decimales infinitos NO
periódicos. Aquellos números que NO se pueden escribir como fracción. Ejemplos: { 2 , p ,
5
3 , ... }
2 Números Reales R. Unión del conjunto de los racionales y los irracionales. Ejemplos: { 7 , 3 p ,
4
8 , ... }
2 Números Imaginarios I. Los números imaginarios I, son todos aquellos números de la forma bi, con b
2
número real e i la unidad imaginaria. Ejemplos: { i , 2i , 3 i ,
i , ... }
3
2 Números Complejos C. Números de la forma z = a + b· i , donde a y b reales e i es la unidad imaginaria.
Ejemplos: { 1 , – i , 3 + 2i , 1 – i , ... }
2. NÚMEROS ENTEROS
a. Operatoria en los Enteros
i. Adición y sustracción
Números de igual signo: para adicionar números
de igual signo se deben sumar los valores
absolutos de ellos conservando el signo común.
Ejemplos:
5 + 7 = 12
;
– 5 – 7 = –12
Números de distinto signo: para adicionar
números de distinto signo, al de mayor valor
absoluto se le resta el de menor valor absoluto y
se conserva el signo del mayor número en valor
absoluto.
Ejemplos:
TIPS:
5 – 7 = –2
;
–5 + 7 = 2
2
Siempre que a un número mayor le restamos uno menor, el resultado es positivo.
2
Siempre que a un número menor le restamos uno mayor, el resultado es negativo.
ii. Multiplicación y división
Números de igual signo: para multiplicar o dividir
dos números de igual signo, se multiplican los
números y el resultado siempre será positivo.
Ejemplos:
5· 7 = 35
;
( – 5 )· ( – 7 ) = 35
10 : 2 = 5
;
( – 10 ) : ( – 2 ) = 5
Números de distinto signo: para multiplicar
o dividir dos números de distinto signo, se
multiplican los números y el resultado siempre
será negativo.
Ejemplos: 5· ( – 7 ) = – 35
;
( – 5 )· 7 = –35
10 : ( – 2 ) = – 5
;
( – 10 ) : 2 = –5
TIPS: Siempre se cumple que:
» La suma o resta de dos números pares, dan como
resultado un número par.
» La suma o resta de dos números impares, dan como
resultado un número par.
» La suma o resta de un número par y un impar, dan
como resultado un número impar.
2
Editorial Moraleja
» La multiplicación de dos números pares, dan como
resultado un número par.
» La multiplicación de un número par y un impar, dan
como resultado un número par.
» La multiplicación de dos números impares, dan
como resultado un número impar.
iii. Prioridad de las operaciones
Cuando se requiere efectuar varias operaciones en un mismo ejercicio, se debe respetar el siguiente orden
de las operaciones: 1º Paréntesis , 2º Potencias y Raíces , 3º Multiplicación y división (de izquierda a derecha),
4º Adición y sustracción.
b. Criterios de divisibilidad
Para determinar de manera rápida los divisores de un número, podemos usar los criterios de divisibilidad.
Un número será divisible por:
2 → Si su última cifra es par.
3 → Si la suma de sus cifras es múltiplo de 3.
7 → Si al multiplicar la cifra de las unidades por 2
y restándola al número formado por las otras
cifras, el resultado es un múltiplo de 7 o 0.
4 → Si sus dos últimas cifras forman un múltiplo de 4
o son ceros.
8 → Si sus tres últimas cifras forman un múltiplo de 8
o son ceros.
5 → Si termina en cero o 5.
9 → Si la suma de sus cifras es múltiplo de 9.
6 → Si es divisible por 2 y 3 a la vez.
10 → Si su última cifra es cero.
c. Números Primos y Compuestos
Números Primos: Enteros positivos que solo son divisibles por uno y por si mismos: { 2 , 3 , 5 , 7 , 11 , ... }
Números Compuestos: Enteros positivos mayores que uno que no son primos: { 4 , 6 , 8 , 9 , 10 , 12 , ... }
El teorema fundamental establece que todo número compuesto se puede expresar de manera única
como el producto de factores primos.
TIPS:
» El menor número primo es el 2, el que además es el único número primo que es par.
» El 1, no es primo ni compuesto.
» El 0, es un número par. Este no es positivo, ni negativo.
d. Mínimo común múltiplo (m.c.m) y máximo común divisor (M.C.D)
i. Mínimo común múltiplo (m.c.m)
El mínimo común múltiplo (m.c.m), es el menor entero positivo que es múltiplo común de dos o más enteros.
2
Métodos para hallar el m.c.m:
a. Tabla de descomposición:
b. Descomposición prima:
Ejemplo:
Ejemplo:
Sean A = 90 y B = 24, determinar el m.c.m
Sean A = 90 y B = 24, determinar el m.c.m
24
90
:2
12
45
:2
6
45
:2
3
45
:3
1 //
15
:3
5
:5
A = 2· 32· 5 y B = 23· 3
∴ el m.c.m entre 90 y 24 es 23· 3 2· 5
1 //
m.c.m =
23· 3 2· 5
∴ el m.c.m entre 90 y 24 es 23· 3 2· 5
Editorial Moraleja
3
ii. Máximo común divisor (M.C.D)
El máximo común divisor (M.C.D), es el mayor entero positivo que es divisor común de dos o más enteros.
2
Métodos para hallar el M.C.D:
a. Tabla de descomposición.
b. Descomposición prima.
Ejemplo:
Ejemplo:
Sean A = 90 y B = 24, determinar el M.C.D
Sean A = 90 y B = 24, determinar el M.C.D
24
90
:2
12
45
:3
4
A = 2· 32· 5 y B = 23· 3
15
M.C.D =
∴ el M.C.D entre 90 y 24 es 2· 3
2· 3
∴ el M.C.D entre 90 y 24 es 2· 3
TIPS: Los números que no tienen factores primos comunes se denominan primos relativos entre sí. En tal caso se
cumple que el m.c.m es el producto de los números y el M.C.D es 1. Por ejemplo, 9 y 10 son primos relativos entre
si, ya que los factores primos de 9 son { 3 , 3 }, y los factores primos de 10 son { 2 , 5 }. Por tanto: el m.c.m entre 9 y 10
es 90 , el M.C.D entre 9 y 10 es 1.
e. Valor Absoluto
El valor absoluto de un número x se escribe |x|, este resultado
corresponde a la distancia que existe entre el número x y el
0, por lo tanto, el valor de |x| es siempre mayor o igual a 0.
Matemáticamente, esto último es: |x|≥ 0.
–3
–2
–1
|–3| = 3
x =*
0
1
2
3
|3| = 3
x, si x $ 0
–x, si x 1 0
i. Propiedades del valor absoluto
El valor absoluto cumple las siguientes propiedades:
1. Multiplicación:
2. División:
a $ b = a$b
3. Potencia:
an = a
a
a
=
b
b
n
3. NÚMEROS RACIONALES
a. Operatoria en Q
Sean a, b, c y d números enteros distintos de cero, se cumple:
4
Adición y sustracción:
Multiplicación:
División:
a c
a$d!b$c
!
=
b d
b$d
a c
a$c
$ = b
b d
$d
a c
a$d
|
=
b d
b$c
Editorial Moraleja
Recíproco de
b
–1
a
b
l=
b
a
a
:
b
b. Operatoria con decimales
i. Adición y sustracción
Para sumar o restar números decimales se ubican las
cantidades enteras bajo las enteras, las comas bajo las
comas, la parte decimal bajo la decimal y a continuación
se realiza la operatoria respectiva.
Ejemplo:
0,247 + 21,65 =
0, 247
+ 21, 65
21, 897
ii. Multiplicación
Para multiplicar dos o más números decimales, se multiplican
como si fueran números enteros, y luego se ubica la coma
en el resultado final, de manera tal que el resultado tenga
la misma cantidad de cifras decimales que los números del
ejercicio en conjunto.
Ejemplo:
1,24 · 0,002 =
Multiplicar 124· 2 = 248
Ubicar la coma manteniendo cinco
cifras decimales: 0,00248
iii. División
Para dividir números decimales, se puede transformar el
dividendo y el divisor en números enteros amplificando por
una potencia en base 10.
Ejemplo:
2,25 : 0,5 =
(Amplificado por 100)
→ 225 : 50 = 4,5
c. Transformación entre decimales y fracciones
i. De decimales finitos a fracciones
Paso 1: En el numerador se escribe el número completo sin la coma.
Paso 2: En el denominador un 1 acompañado de tantos ceros como dígitos
existan en la parte decimal.
Ejemplo:
342
3, 42 =
100
ii. De decimales periódicos a fracciones
Paso 1: En el numerador se escribe el número completo sin la coma y se le
resta la parte no periódica.
Paso 2: En el denominador tantos nueve como dígitos posea el período.
Ejemplo:
145 – 1
99
1, 45 =
iii. De decimales semi-periódicos a fracciones
Paso 1: En el numerador se escribe el número completo sin la coma y se le
resta la parte no periódica.
Paso 2: En el denominador se escribe tantos nueve como dígitos posea el
período, seguidos de tantos ceros como dígitos tenga el ante–período.
Ejemplo:
2421 – 24
2, 421 =
990
d. Relación de orden en los racionales
Para hallar la relación de orden entre números racionales, se puede utilizar alguno de los siguientes métodos:
i. Multiplicación cruzada
iii. Igualar denominadores
ii. Igualar numeradores
iv. Convertir a número decimal
» Recordar que los dígitos decimales de acuerdo a su posición
reciben los siguiente nombres:
c m dm
UM C D U , d 5
6 :
5 5
: 5 5
ad
id
Un
il
M ena ena dad ima ima ima sima
c
és ilé
és
de ent ec Uni
dé ent mil
D
m
C
c
ez
di
Editorial Moraleja
5
e. Aproximaciones – Tipos
Ejemplo:
Redondeo
2
Redondear a la centésima
los números 3,1421 y 1,8671
Paso 1: Identificar la posición a la que se quiere
redondear.
→ 3,14 y 1,87.
Paso 2: Considerar la cifra decimal inmediatamente
siguiente a la que determine la aproximación.
Paso 3: Si dicha cifra es menor que 5, no hay
modificaciones en las cifras que se conservan. Si dicha
cifra es mayor o igual que 5, la cifra por aproximar se
debe aumentar en una unidad.
Truncamiento
2
Ejemplo:
Paso 1: Identificar la posición a la que se quiere truncar.
Truncar a la centésima los
números 3,1421 y 1,8671
Paso 2: Considerar las cifras decimales hasta la posición
que se determinó.
→ 3,14 y 1,86.
Aproximación por defecto
2
Ejemplo:
Paso 1: Identificar la posición a la que se quiere
aproximar.
Aproximar por defecto a la
décima el número 3,47 → 3,4
Paso 2: Considerar las cifras decimales hasta la posición
que se determinó.
Aproximación por exceso
2
Ejemplo:
Paso 1: Identificar la posición a la que se quiere
aproximar.
Aproximar por exceso a la
unidad el número 15,28 → 16
Paso 2: La cifra por aproximar se debe aumentar en
una unidad.
4. NÚMEROS REALES
a. Operaciones en los Números Reales
2 La operación entre racionales da como resultado un número racional, exceptuandose la división por
cero.
2 La operación entre un racional y un irracional da como resultado un número irracional, exceptuandose
la multiplicación y la división por cero.
2 La operación entre números irracionales no siempre resuresulta número irracional.
5. POTENCIAS
a. Propiedades
2
a m· a n = a m + n
2
am : an = am – n
2
a m· b m = ( a· b ) m
2
2
6
a
m
:b
n m
(a )
m
= (a : b)
=a
ó
b
–n
n
a
b
l= c m, con a, b ≠ 0
b
a
2
a0 = 1
2
0 n = 0, si n > 0
2
1n = 1
2
0 0 no está definido
m· n
=
1
n
a
a
m
Editorial Moraleja
–n
2
b. Ecuación Exponencial
Ecuación exponencial es aquella que tiene la incógnita en el exponente. Para resolver una ecuación
exponencial se debe tratar de igualar las bases, aplicando las propiedades correspondientes. Las bases
deben ser distintas de cero, uno y menos uno.
2 3 x –1 = 2 x+2
Ejemplo:
$
^3x – 1 h = ^x + 2 h
Luego, se deben igualar los exponentes y resolver la ecuación resultante.
6. RAÍCES
a. Propiedades
Las siguientes propiedades se cumplen, sí y solo sí, a y b ! R + ; m y n ! Z +.
2
n
a $n b = n a$b
2
n
a m = ^n a h
2
n m
2
n ^ah m
;
n
a : n b = n a:b
n ^ah $ m ^bh
2
m
a = m$n a
= n $ k ^ah m $ k
= n $ m ^ah m $ ^bh n
2
b $ n ^ah = n ^ah $ b n
2
n
^ah m = ^ah
m
n
^a h 2 = a , para todo a ! R.
2
b. Racionalización
i. Caso 1: Raíz cuadrada:
a
b c
a
b+ c
ii. Caso 2: Binomio con raíces cuadradas:
iii. Caso 3: Raíz no cuadrada:
$
a
n
b
m
a $
b c
a $^ b – ch
a
$c b – c m
=
b–c
b+ c
b– c
$
$
c = a c
b
c
n
a
n
b
m
$
n
b
n–m
b
n–m
=
a$n b
b
n–m
c. Ecuación Irracional
Ecuación irracional es aquella que tiene la incógnita en el sub–radical de una raíz. Ejemplo:
Es importante que el(los) valor(es) encontrado(s) sea comprobado en la ecuación original.
^x + 1h = 5
7. PRODUCTOS NOTABLES
2
Cuadrado de binomio:
^a + b h 2 = a 2 + 2ab + b 2
2
^a – bh ^a + bh = a 2 – b 2
^a – b h 2 = a 2 – 2ab + b 2
2
Binomios con termino común:
2
^x + a h ^ x + bh = x 2 + ^a + b h $ x + a $ b
2
Suma y resta de cubos perfectos:
^a + b h ^a 2 – ab + b 2 h = a 3 + b 3
^a – b h ^a 2 + ab + b 2 h = a – b 3
Suma por diferencia:
Cubo de binomio:
^a + b h 3 = a 3 + 3a 2 b + 3ab 2 + b 3
^a – b h 3 = a 3 – 3a 2 b + 3ab 2 – b 3
2
Cuadrado de un trinomio:
^a + b + c h 2 = a 2 + b 2 + c 2 + 2ab + 2bc + 2ac
Editorial Moraleja
7
8. ECUACIÓN DE PRIMER GRADO
Una ecuación se denomina de primer grado o lineal si el mayor exponente de la incógnita es 1.
a. Ecuaciones Literales
Son ecuaciones que, además de la incógnita, contienen otras letras que representar variables. Para
resolverlas, se debe identificar la letra que representa la incógnita y despejarla.
b. Ecuaciones valor absoluto
Las ecuaciones con valor absoluto que estudiaremos, se
pueden reducir a la forma: x = a.
Ejemplo:
x + 4 = 12
Para resolverlas, debemos plantear dos ecuaciones
lineales a partir de la ecuación original, siguiendo el
esquema:
x =a
55
x + 4 = 12
x1 = 8
5 5 46
x=a
– (x) = a
Como vemos, obtenemos dos ecuaciones lineales,
que debemos resolver por separado para obtener las
soluciones de la ecuación original.
46
– (x + 4) = 12
– x – 4 = 12
– x = 16
x 2 = – 16
9. SISTEMAS DE ECUACIONES
Dos ecuaciones de primer grado, que tienen ambas las mismas dos incógnitas, constituyen un sistema
ax + by = c
de ecuaciones lineales. La forma general de un sistema de ecuaciones de primer grado es:
,
dx + ey = f
donde a, b, c, d, e y f son números reales.
a. Métodos de resolución de sistemas de ecuaciones
i. Método de Sustitución
Se debe despejar una de las variables en una de las ecuaciones y luego reemplazarla en la otra ecuación,
generándose así una ecuación con una incógnita.
ii. Método de Igualación
Se debe despejar la misma variable en ambas ecuaciones y luego éstos resultados se igualan, generándose
así una ecuación con una incógnita.
iii. Método de Reducción
Se deben igualar los coeficientes numéricos de una de las incógnitas, en ambas ecuaciones, multiplicando
ambos miembros convenientemente, obteniéndose un sistema equivalente al dado, y luego se suman o
restan ambas ecuaciones, resultando así una ecuación con una incógnita.
b. Análisis rápido de sistemas de ecuaciones
Dado el sistema _b
b $
`
ax + by = c
bb
dx + ey = f
a
8
Si:
a
b
! e
d
Entonces el sistema
tiene una solución.
Editorial Moraleja
Si:
a b
c
=
!
d e
f
Entonces el sistema
no tiene solución.
Si:
a b c
=
=
d e
f
Entonces el sistema
infinitas soluciones.
10.
DESIGUALDADES
Si a, b, c son números reales, las desigualdades cumplen las siguientes propiedades:
2
Sí, a < b, entonces a + c < b + c
2
Sí, a < b y c > 0 , entonces a· c < b· c
2
Sí, a < b y c < 0 , entonces a· c > b· c
2
2
11.
Sí, 0 < a < b ó a < b < 0 , entonces 1 > 1
a b
Sí a < 0 < b , entonces 1 < 1
a b
2
Sí, 0 < a < b
y n un número natural,
entonces a n < b n
2
Sí, a < b < 0
y n un número natural,
entonces a 2n > b 2n
2
Sí, a < b < 0
y n un número natural,
entonces a 2n + 1 < b 2n + 1
INECUACIONES
a. Inecuaciones de primer grado con una incógnita
Son desigualdades que se pueden reducir a una de las formas siguientes:
ax + b ≥ 0
;
ax + b ≤ 0
;
ax + b > 0
;
ax + b < 0
Para resolverlas se debe despejar la incógnita x, teniendo en cuanta las propiedades de las desigualdades.
NOTAS:
2
Si al despejar la incógnita en una ecuación esta desaparece y queda:
2
Una desigualdad VERDADERA, la solución será R. Ejemplo: 0 ≥ –5
2
Una desigualdad FALSA, la solución será Ø. Ejemplo: 3 < 1
b. Inecuaciones de segundo grado
Cuando tenemos una desigualdad expresada de la forma: ax 2 + bx + c ≤ 0 o ax 2 + bx + c ≥ 0. El proceso
de resolución es:
1 ro. Se debe dejar cero a un lado de la igualdad.
5 to. Reemplazar para cada factor un valor de
cada rango y analizar si signo ( + ó – ).
2 do. Factorizar la expresión.
6 to. Analizar para cada rango, si el producto de
los factores será + ó – .
3 ro. Encontrar los puntos críticos de la ecuación
(valores que hacen cero cada factor).
7 to. Construir el conjunto solución con los
intervalos que cumplen con la condición inicial
> 0 ó < 0.
4 to. Construir una tabla con factores y puntos
críticos entre – ∞ y + ∞ , formando rangos.
2
12.
Este mismo proceso se aplica también cuando queremos resolver inecuaciones fraccionarias.
LOGARITMOS
Definición: log a b = c + ac = b . Además se debe cumplir que: b > 0 ; a ≠ 1 ; a > 0.
a. Propiedades
2
2
log 10 a = log a
log a 1 = 0
2
2
log a a m = m
a
log a b
=b
2
log a a = 1
2
log a m· n = log a m + log a n
2
log e x = ln x
2
log a c
n
2
log a b = n $ log a b
2
log a b =
log c b
log c a
b
= log a b – log a c
m
c
Editorial Moraleja
9
b. Relación de orden de logaritmos
Sean los argumentos, a, b números reales positivos y las bases n, m números reales positivos distintos de 1.
Para ordenar logaritmos podemos utilizar alguno de los siguientes métodos, según sea el caso.
i. Caso 1. Iguales argumentos
Para ordenar logaritmos de iguales argumentos y bases mayores que 1, basta comparar las bases.
•
Si se cumple que n < m, entonces log m a < log n a
ii. Caso 2: Iguales bases
Para ordenar logaritmos de igual base, basta comparar los argumentos.
•
Si, n > 1 y a < b , entonces log n a < log n b
•
Si, 0 < n < 1 y a < b , entonces log n a > log n b
iii. Caso 3: Distintas bases y distintos argumentos
En caso que tanto los argumentos como las bases sean distintas, una posibilidad seria cambiar las expresiones
hasta llegar a alguna con base común, aplicando propiedades.
c. Ecuación Logarítmica
Ecuación logarítmica es aquella que tiene la incógnita en el argumento de un logaritmo. Para resolver, se
deben igualar los argumentos y luego, resolver la ecuación resultante.
Ejemplo: log ( 3x – 1 ) = log ( x + 2 ) $ ^3x – 1 h = ^x + 2 h .
sea comprobado en la ecuación original.
Es importante que el(los) valor(es) encontrado(s)
d. Ecuación exponencial de distinta base
Cuando tenemos una ecuación exponencial en la que no es posible igualar bases, aplicamos logaritmos,
esto lo hacemos ya que una de las propiedades del logaritmo permite llevar el término que está en el
exponente del anti-logaritmo al numerador.
Ejemplo: 2 3x – 1 = 3 x + 2
13.
$
log 2 3x – 1 = log 3 x + 2
$
^3x – 1 h $ log 2 = ^x + 2 h $ log 3
$
Despejar x
NÚMEROS COMPLEJOS
Un número complejo es de la forma ( z = a + b· i ), donde: a: es la parte real del complejo y se escribe como
Re (z) ; b: es la parte imaginaria del complejo y se escribe como Im (z).
a. Unidad imaginaria
Unidad imaginaria, “ i ” y cuyo cuadrado es –1. Es decir,
–1 = i .
Potencias de i:
En una secuencia de potencias, se cumple:
TIPS:
i 4n + p = i p , con n ! R +0 y 0 ≤ p ≤ 4
2
i0 = 1
2
La suma de cuatro potencias consecutivas de i es 0
2
El producto de cuatro potencias consecutivas de i es –1
b. Conjugado de un complejo
Sea el complejo z = a + bi , su conjugado es z = a – bi
10
Editorial Moraleja
c. Representación
Existen diversas formas de representar números complejos. Éstas son:
2 Forma binomial:
2 Par ordenado:
a + bi
a + bi " Par ordenado: ( a , b )
2 Vector: Cuyo punto de inicio es el origen y su punto de llegada corresponde al par ordenado.
d. Adición y sustracción de complejos
Para sumar o restar dos números complejos, operamos las respectivas partes reales y partes
imaginarias entre sí:
Esto es: z1 = a + bi
y
z 2 = c + di
Entonces las suma: z1 + z 2 = ( a + c ) + ( b + d )· i
Entonces la resta: z1 – z 2 = ( a – c ) + ( b – d )· i
NOTAS:
2
El neutro aditivo de un complejo es ( 0 , 0) = 0 + 0i
2
El inverso aditivo de un complejo z = a + bi , es –z = –a – bi
e. Valor absoluto de un complejo
Si z = a + bi, entonces el módulo de z es |z| , tal que z = a 2 + b 2 .
NOTA:
2
El módulo de un complejo z, también se puede expresar como z .
Propiedades del valor absoluto
El módulo cumple las siguientes propiedades:
z1 $ z2 = z1 $ z2
z1
z1
z2 = z2
zn = z
n
f.Multiplicación de complejos
Para multiplicar 2 números complejos se debe hacer de la misma forma en que se multiplicaban dos
binomios. Luego se debe reducir.
g. Inverso multiplicativo de un complejo
Sea z = a + bi, entonces el recíproco o inverso multiplicativo de z es :
1
1
.
z –1 = z o z –1 =
a + bi
z –1 =
1
a – bi
$
a + bi a – bi
a – bi
Es importante que los términos con “i“ no queden en el denominador. De
ser así, se debe “racionalizar“.
=
Para racionalizar un complejo, debe amplificarse por el conjugado del
denominador y luego reducir:
=
a – bi
a2 – b2i2
=
a – bi
a2 +b2
a 2 – _ bi i
2
h. División de complejos
z
Si z1 = a + bi y z 2 = c + di , con z 2 distinto de cero, la división entre ellos se expresa: z 12 . Como se explica
anteriormente, debemos racionalizar nuestro resultado.
Ejemplo: Si z 1 = 2 + 3i y z 2 = 4 – i
_ 2 + 3i i
_ 4 + i i 8 + 2i + 12i + 3i 2
z1
5
14
8 + 14i + 3i 2
8 + 14i – 3
5 + 14i
ó
=
=
=
=
+
i
z2 = _ 4 – i i
17
17 17
16 + 1
_4 + ii
16 – i 2
16 – i 2
reemplazamos i 2 por –1
Editorial Moraleja
11
14.
ECUACIÓN DE SEGUNDO GRADO
Una ecuación de segundo grado es aquella de la forma ax 2 + bx + c = 0 , con a, b y c coeficientes reales
y a ≠ 0. Todas poseen dos soluciones, ya sea en el conjunto de los números reales o en el de los complejos.
a. Métodos resolución
i. Factorizar
Se debe factorizar la expresión como ( x – x1 )( x – x 2 ) = 0. Las soluciones de la ecuación serán x1 y x 2..
Ejemplos:
Resolver: x 2 – 2x = 0
Resolver: x 2 – 4 = 0
x( x – 2 ) = 0
x=0
x1 = 0
ó
(x – 2) = 0
; x2 = 2
Resolver: x 2 – 5x + 6 = 0
( x + 2 )( x – 2 ) = 0
( x – 2 )( x – 3 ) = 0
(x + 2) = 0
(x – 2) = 0
x 1 = –2
ó
(x – 2) = 0
; x2 = 2
x1 = 2
ó
(x – 3) = 0
; x2 = 3
ii. Completando cuadrados
Se debe reescribir la ecuación de segundo grado de
modo que quede escrita de la forma:
( x – h )2 + k = 0
Ejemplo:
Resolver: x 2 + 6x + 5 = 0
2
x + 6x + 5 = 0
Luego despejar x
2
x +2$x$3+5 = 0
2
x + 6x + 9 – 9 + 5 = 0
14444442444443
^x + 3h 2 – 4 = 0
^x + 3h 2 = 4 /
^x + 3h = ! 2
x=k ! h
x = –3!2
∴ x 1 = –1
; x 2 = –5
iii. Fórmula general
Este método requiere simplemente que se reemplacen los
valores de a, b y c en la fórmula para hallar la solución.
x=
Ejemplo:
Resolver: 3x 2 – x – 2 = 0
a = 3 , b = –1 , c = –2
2
– b ! b – 4ac
2a
Se recomienda utilizar solo cuando no es posible factorizar
o completar el cuadrado.
x=
– ^ –1 h ! ^ –1 h 2 – 4 $ 3 $ ^ –2 h
2$3
x=
1 ! 1 + 24
6
x=
1 ! 25
1!5
=
6
6
x1 =
1+5
=1
6
x2 =
1 – 5 –2
=
6
3
b. Propiedades de las soluciones
Si x1 y x 2 son las soluciones de la ecuación de segundo grado de la forma ax 2 + bx + c = 0, entonces siempre
se cumplen las siguientes propiedades:
–b
x 1+ x 2 = a
12
Editorial Moraleja
,
c
x 1· x 2 = a
c. Análisis de las soluciones utilizando el discriminante
El discriminante es: D = b2 – 4ac. El signo del discriminante determina la naturaleza de las soluciones:
•
Si D > 0 , entonces las soluciones son números Reales y distintos
•
Si D = 0 , entonces las soluciones son números Reales e iguales
•
Si D < 0 , entonces las soluciones son números Complejos y distintos
•
15.
CONCEPTOS BÁSICOS DE FUNCIONES
Una función de A en B es una relación que asigna a cada elemento
del conjunto A uno y sólo un elemento del conjunto B. Se expresa
como, f: A $ B
f(x)
El conjunto A, representa los valores que puede tomar la función.
Este conjunto lleva por nombre, Dominio de la función. Cada
elemento del dominio recibe el nombre de pre–imagen.
El conjunto B, representa a los valores que toma la función. Este
conjunto se llama el Recorrido de la función. A cada elemento del
recorrido se le llama imagen.
En el gráfico sagital adjunto muestra que para que la función este
bien definida, se debe cumplir que de todos los elementos del
conjunto de salida “A”, estén asociado a solo un elemento en el
conjunto de llegada “B”.
A
B
M
1
N
2
P
3
Q
4
Dominio
Recorrido
Un elemento en el conjunto de llegada “B”, puede estar asociado
a más de un elemento en el conjunto de partida “A”.
a. Composición de funciones
Sea f: A $ B y g: B $ C , podemos hallar una función
g(f(x)), que vaya de A $ C. Tal como lo muestra la figura.
g(x)
f(x)
A
B
C
M
1
r
N
2
s
P
3
t
Q
4
w
Ejemplo:
Sea f y g funciones reales definidas
por: f(x) = 2x – 3 y g(x) = 4 – 5x. Hallar
g(f(x)) :
g(f(x)) = 4 – 5 (2x – 3)
= 4 – 10x + 15
= –10x + 19
∴ g(f(x)) = –10x + 19
g( f(x) )
Editorial Moraleja
13
b. Función inversa
Sea f: A $ B
y podemos hallar una función f –1(x), que vaya
de B $ A. Tal como lo muestra la figura adjunta. Otra forma de
analizarlos es si un punto ( x , y ) pertenece a la función f(x), entonces
el punto ( y , x ) pertenecerá a la función f –1(x).
Para determinar la expresión algebraica de la función inversa, se
despeja la variable x de la expresión y = f(x) y luego se intercambian
la variable x por la y.
f(x)
A
B
M
1
N
2
P
3
Q
4
f–1(x)
Siempre se cumple que los puntos (x , y) e (y , x), son simétricos con
respecto a la recta y = x, por tanto, las gráficas de estas funciones
serán simétricas con respecto a la recta y = x.
Ejemplo:
y
Además, es importante mencionar que no todas las funciones
poseen inversa. Solo las funciones biyectivas tienen función inversa.
f(x)
f(x)
1
1
–1
x
y=x
c. Clasificación de funciones
i. Función Inyectiva
ii. Función Epiyectiva
Una función es epiyectiva
cuando cada valor de recorrido
corresponden distintos valores en
el recorrido.
tiene al menos un valor del
dominio.
f(x)
Una función es biyectiva cuando
es inyectiva y epiyactiva a la vez.
f(x)
0
M
Q
4
Q
Dominio
Recorrido
Dominio
1
N
2
P
3
Q
4
Dominio
Recorrido
2
P
3
M
1
N
2
P
f(x)
M
1
N
3
Recorrido
f(x)
f(x)
f(x)
4
3
2
4
3
2
4
3
2
1
1
1
0
M N P
Q
x
» Gráficamente, para ver si una
función es inyectiva, podemos
dibujar paralelas al eje x. Estas
deben cortar A LO MÁS en un
punto a la función.
14
iii. Función Biyectiva
Una función es inyectiva, cuando
a distintos valores del dominio, le
Editorial Moraleja
M N P
Q
x
» Gráficamente, para ver si una
función es epiyectiva, podemos
dibujar paralelas al eje x. Estas
deben cortar AL MENOS en un
punto a la función.
M N P
Q
x
» Gráficamente, para ver si una
función es inyectiva, podemos
dibujar paralelas al eje x. Estas
deben cortar SIEMPRE en un
punto a la función.
d. Traslación de funciones
Sea y = f(x) una función. Sean h y k números positivos son positivos, entonces se cumple:
i. Desplazamiento vertical
ii. Desplazamiento
horizontal
y = f(x) + k, es la función f(x)
desplazada k unidades en el eje
y.
iii. Desplazamiento
compuesto
x.
2
Si k > 0 el desplazamiento es
en hacia arriba
2
Si h > 0 el desplazamiento es
a la derecha
2
Si k < 0 el desplazamiento es
hacia abajo
2
Si h < 0 el desplazamiento es
a la izquierda
f(x)
y = f(x – h) + k es la función f(x)
desplazada k unidades en el
eje y h unidades en el eje x.
y = f(x – h), es la función f(x)
desplazada h unidades en el eje
y = f(x) + k
f(x)
y = f(x + h) + k
f(x)
y = f(x – h)
k
k
x
h
x
x
–h
e. Reflexión de funciones
2
Reflexión con respecto al eje y
2
y
y
Si en una función f(x), sustituimos (x) por (–x),
la gráfica de f(–x) es el reflejo la primera en
torno al eje y.
f(–x)
f(x)
1
Reflexión con respecto al eje x
y
1
x
y
f(x)
Si a una función f(x), ante-ponemos un signo
menos, “–f(x)” , la gráfica de –f(x) es el reflejo
la primera en torno al eje x.
x
x
x
–f(x)
16.
FUNCIÓN AFÍN Y LINEAL
2
Función afín
2
Una función afín es de la forma:
f(x) = mx + n , con m, n ! R y m ≠ 0.
f(x)
Función lineal
2
Una función lineal es de la forma:
f(x) = mx , con m, ! R y m ≠ 0.
Función identidad
La función identidad es f(x) = x
f(x)
f(x)
2
1
x
–1
x
1
2
x
–1
» La función lineal expresa una
proporcionalidad directa entre
las variables x y f(x).
Editorial Moraleja
15
17. FUNCIÓN CUADRÁTICA
Sea a, b, c ! R y a ≠ 0, se denomina función cuadrática, a una
función de la forma: f ( x ) = ax 2 + bx + c
a. Concavidad
Concavidad es la abertura que tiene la parábola. De acuerdo al valor que toma a, se dan los siguientes
casos:
2
Si a > 0 , entonces la parábola se abre hacia arriba
2
Si a < 0 , entonces la parábola se abre hacia abajo
b. Dominio y recorrido
El dominio de una función cuadrática es el conjunto R. El recorrido depende de la concavidad de la
parábola.
Si a < 0
→
–3 , k @
Rec: @
→
Si a < 0
k ,36
Rec: 6
f( x )
f( x )
k
h
h
x
x
k
c. Apertura
•
•
f( x )
Si, |a| > 1, la gráfica de f1( x ) = ax 2 es más
cerrada en torno al eje de simetría que la
gráfica de f( x ) = x 2.
f1( x ) = ax2
f( x ) = x2
f2( x ) = ax2
Si, 0 < |a| < 1, la gráfica de f2( x ) = ax 2 es más
abierta en torno al eje de simetría que la
gráfica de f( x ) = x 2.
x
d. Uso del discriminante
Recordemos del capítulo de ecuaciones de segundo grado, que el discriminante es: D = b2 – 4ac .
Dependiendo de su signo, podíamos conocer la naturaleza de las soluciones.
En funciones lo utilizaremos para conocer si la función corta o no al eje de las abscisas.
f( x )
x
16
f( x )
f( x )
x
x
D>0
D=0
D<0
La parábola intersecta en dos
puntos al eje x
La parábola intersecta en un
punto al eje x.
También se dice que el eje x
es tangente a la parábola.
La parábola NO intersecta al
eje x
Editorial Moraleja
e. Intersección con los ejes
La parábola siempre intersecta al eje de las ordenadas y lo hace en el punto ( 0 , c ).
La parábola intersecta al eje de las abscisas en x1 y x 2 , que corresponden a las soluciones de una ecuación
de segundo grado, donde se iguala f( x ) = 0. Las coordenadas de intersección con el eje x son: ( x1 , 0 ) y
( x2 , 0 )
f. Eje de simetría y vértice
Sea la ecuación de segundo grado de la forma ax 2 + bx + c = 0 ,
cuyas soluciones son x1 y x 2 .
f( x )
xv
El eje de simetría de la parábola es una recta que divide a esta
curva en dos partes congruentes. Para determinar el eje de simetría
podemos hacerlo de alguna de estas dos maneras:
XV = x1 + x2
2
ó
XV =
x1
–b
2a
yv
El vértice de la parábola es el punto de intersección de ésta con su
eje de simetría. El vértice se puede determinar de tres maneras:
– b 4ac – b 2 m
V = ^X V , f ^X V hh V = c
,
2a
4a
x
x2
( xv , yv )
f ^x h = a^x – hh 2 + k " V = ^ h , k h
g. Máximo y mínimo
Si a < 0
Si a > 0
f( x )
k
f( x )
Pmax ( h , k )
h
h
x
x
k
En este caso, la función alcanza un valor máximo
( k ) , cuando la variable independiente toma el
valor de h.
Pmin ( h , k )
En este caso, la función alcanza un valor mínimo
( k ), cuando la variable independiente toma el
valor de h.
h. Desplazamientos
Si la función está escrita de la forma:
f( x ) = a· ( x – h ) 2 + k
La parábola se traslada h unidades en el eje x y k unidades en
el eje y, obteniéndose el nuevo vértice de coordenadas ( h , k ).
Estos desplazamientos son respecto a una parábola con vértice
en el origen.
f( x )
k
Si la función está escrita de la forma f( x ) = ax 2 + c, su
desplazamiento solo será vertical de acuerdo al valor de c.
•
Si, c > 0 , se desplaza c unidades hacia arriba.
•
Si, c < 0 , se desplaza c unidades hacia abajo.
h
Editorial Moraleja
x
17
18.
FUNCIÓN RAÍZ CUADRADA
Sea “ x ” es un número real no negativo, se define la función raíz
cuadrada de “ x ” por: f ^ x h = x .
Representación gráfica
f(x)
Propiedades
2
Dom: R +0
; Rec: R +0
La gráfica intersecta a los ejes en el origen ( 0 , 0 ).
2
La función es creciente.
2
De manera más general, la representación canónica de la
2
19.
1
función raíz cuadrada es: f ^ x h = a $ !^x – h h + k , con a > 0.
1
x
FUNCIÓN EXPONENCIAL
Sea “ x ” es un número real, se define la función exponencial de “ x ”
por: f(x) = bx , con b ! R+ y b ≠ 1
Representación gráfica
f(x)
Propiedades
f(x) = 2x
Rec: R +
2
Dom: R
;
2
La gráfica intersecta al eje de las y en el punto ( 0 , 1 ).
2
La gráfica no corta al eje x
2
Si b > 1, entonces f(x) = bx , es creciente
2
Si 0 < b < 1, entonces f(x) = bx , es decreciente
4
b>1
2
1
–2 –1
1 2
x
f(x)
0<b<1
4
2
1
–2 –1
f (x ) = b
1 2
x
1l
2
x
a. Aplicaciones de la función exponencial
2
Interés compuesto
La
formula
de
n
2
interés
Cf = Ci $ _1 + ri, donde:
compuesto
es:
Z
] Cf : Capital final
]] C : Capital inicial
i
[
] r : Tasa de int eres
] n : Nº de periodos
\
18
Editorial Moraleja
Crecimiento exponencial
La fórmula de crecimiento exponencial es:
n
Cf = Ci $ _TCi, donde:
Z
] Cf : Capital final
]] C : Capital inicial
i
[
] TC : Tasa de crecimiento
] n : Nº de periodos
\
20.
FUNCIÓN LOGARÍTMICA
Sea “ x ” es un número real no negativo, se define la función
logarítmica de “ x ” por:
Representación gráfica
f (x) = log 2 x
Propiedades
2
1
2
Dom: R +
2
La gráfica intersecta al eje y en el punto ( 1 , 0 ).
2
La gráfica no corta al eje x.
2
Si b > 1, entonces f(x) = log b x , es creciente
2
Si 0 < b < 1, entonces f(x) = log b x , es decreciente
2
De manera más general, la representación canónica
de la función exponencial es: f(x) = a· log b ( x – h ) + k
;
b>1
f(x)
f(x) = log b x , con b ! R+ y b ≠ 1
Rec: R
–1
–2
1 2
4
x
0<b<1
f(x)
f (x) = log b 1 l
x
2
2
1
–1
–2
21.
4
2
x
1
FUNCIÓN POTENCIA
La función potencia f: R $ R es una función de la forma f(x) = a· xn , donde a es un número real, distinto
de 0, y n es un número natural distinto de 1. La función potencia esta definida para los números reales y su
gráfica depende del exponente.
22.
ÁNGULOS
i. Ángulos formados por rectas paralelas cortadas por una transversal - Casos Frecuentes
Si R1 // R2 , entonces se cumple:
b
R1
R1
R1
b
R1
a
a
d
R2
a
a=b
23.
a
R2
R2
a=b
b
b
R2
a + b = 180º
a+b=d
DIVISIÓN DE TRAZOS
División interna
Si un punto P divide al trazo AB en la razón m : n , entonces se cumple:
AP : PB = m : n
m· k
A
Editorial Moraleja
n· k
P
B
19
24.
TRIÁNGULOS
En los triángulos siempre se cumplen las siguientes propiedades:
2
Suma de las medidas de los ángulos interiores es igual a 180°.
a + b + γ = 180º
A
2
Suma de las medidas de los ángulos exteriores es igual a 360°.
2
La medida de cada ángulo exterior es igual a la suma de las
medidas de los ángulos interiores no adyacentes a él.
a’
a
a` + β` + γ` = 360º
a` = b + γ
b` = γ + a
γ γ’
b` b
C
B
γ` = a + b
a. Clasificación de los triángulos según sus lados
Triángulo escaleno
Triángulo isósceles
Triángulo equilátero
C
C
C
γ
γ
a
b
A
a
b
a
c
B
B
Tiene sus tres lados y sus tres
ángulos de distinta medida.
a
60º
a
c
a
A
A
Tiene dos lados y dos ángulos
de igual medida. El lado
distinto se llama base. De la
figura: el ∆ ABC es isósceles
de base AB o bien se puede
decir que es isósceles en C.
a≠b≠c
a≠b≠γ
a
a
60º
a
60º
B
Tiene sus tres lados y sus tres
ángulos de igual medida.
Cada ángulo interior mide
60º.
b. Otras relaciones en triángulos
i. Relación entre los lados
En todo triángulo, la medida de cada lado es
menor que la suma de las medidas de los otros
dos y mayor que la diferencia (positiva) de las
medidas de los otros dos. En la figura adjunta, se
debe cumplir:
lc – bl < a < b + c
lc – al < b < a + c
C
γ
b
a
B
a
b
c
la – bl < c < a + b
ii. Relación entre los ángulos
En todo triángulo, a mayor ángulo se opone mayor lado y viceversa. En la figura adjunta:
Si, a < b < c , entonces debe cumplir , a < b < γ
20
Editorial Moraleja
A
25.
ELEMENTOS SECUNDARIOS DEL TRIÁNGULO
i.
Altura
ii.
C
Bisectriz
C
E
F
γ γ
O
A
I
•
a
B
D
A
b
b
a
B
El punto de intersección de las alturas se
llama ortocentro.
El punto de intersección de las bisectrices se
llama incentro y este corresponde al centro
de una circunferencia inscrita en el triángulo.
iii.
iv.
Simetral
Mediana
C
C
x
x
x
A
F
O
I
I
x
x
B
A
El punto de intersección de las simetrales se
llama circuncentro y este corresponde al
centro de la circunferencia circunscrita al
triángulo.
E
I
I
D
I
B
2
La mediana es el segmento que une los
puntos medios de los lados del triángulo.
2
Las medianas son siempre paralelas al lado
opuesto y además miden la mitad del lado
al cual son paralelas.
2
Las medianas dividen al triángulo en
cuatro triángulos congruentes, cada uno
de ellos semejante al triángulo mayor.
Editorial Moraleja
21
v. Transversal de gravedad
La transversal de gravedad es el segmento
que une un vértice con el punto medio del
lado opuesto. El punto de intersección de las
transversales se llama centro de gravedad.
C
E
F
G
A
B
D
Propiedades:
2
Si ∆ ABC es rectángulo en C, entonces:
2
CD = AD = DB
El centro de gravedad divide a cada
transversal en la razón 2: 1.
Esto es, CG : GD = 2 : 1
C
C
2k
G
k
A
2
A
B
D
En todo triángulo, cada transversal de
gravedad lo divide en dos triángulos
equivalentes (igual área).
2
B
D
Las tres transversales lo dividen en seis
triángulos equivalentes (igual área).
C
C
E
A1
F
A1
A6
A2
A
A3
A5
A
B
E
A2
A4
B
D
vi. Teoremas referentes a un triángulo isósceles y equilátero.
Triángulo Isósceles
Triángulo Equilátero
C
C
γ γ'
F
x
A
a
x
D
a
G
B
CD = hc = tc = bc = sc
Editorial Moraleja
A
E
30º
30º
30º
30º
Sea un triángulo isósceles de base AB. Los
elementos secundarios correspondientes
coinciden con respecto al lado distinto o
base.
22
30º 30º
D
B
En un triángulo equilátero coinciden TODOS
los elementos secundarios correspondientes
a cualquier lado. Además, coinciden los
puntos singulares o puntos de intersección.
26.
PITÁGORAS Y EUCLIDES
a. Teorema de Pitágoras
En todo triángulo rectángulo, se cumple que la suma de las áreas
de los cuadrados construidos sobre sus catetos, es igual al área del
cuadrado construido sobre su hipotenusa.
B
c
a
a2 + b2 = c2
C
A
b
i. Tríos Pitagóricos
La tabla adjunta muestra los tríos pitagóricos más utilizados.
Cateto
Cateto
3
4
5
5
12
13
8
15
17
7
24
25
20
21
29
Otros tríos pitagóricos pueden surgir de la amplificación de tríos
base, como por ejemplo el trío: 6 , 8 , 10, surge de la amplificación
por 2 del trío: 3 , 4 , 5
Hipotenusa
ii. Triángulos Notables
45º
a
60º
a n2 + 1
a 2
2a
a
a
30º
45º
a
a 3
a· n
b. Teorema de Euclides
Si en un triángulo rectángulo ( ∆ ABC rectángulo en
C ), se dibuja una altura desde el ángulo recto, ésta
divide a la hipotenusa en dos proyecciones ( p y q:
proyecciones de los catetos a y b, respectivamente ),
entonces se producen las siguientes relaciones:
C
a
b
hc
A
B
p
q
c
2
Fórmulas referentes a la altura
h2 = p $ q
c
27.
2
Fórmulas referente a los catetos
a2 = q· c
h c = ac$ b
ÁREAS Y PERÍMETROS EN TRIÁNGULOS
b2 = p· c
C
i. Área: A T = base $2altura
altura
ii. Perímetro: PT = lado + lado + lado
B
A
base
Editorial Moraleja
23
iii. Cálculo de áreas - Casos frecuentes
2
Triángulo rectángulo
AT =
2
Triángulo obtusángulo
cateto $ cateto a $ b
=
2
2
AT =
Triángulo equilátero
2
base $ altura
2
A TE =
^lado h 2 3
=
a2 3
4
^lado h 3
=
a 3
2
h TE =
2
C
C
B
c
a
C
28.
4
a
altura
B
A
A
b
a
A
B
a
base
CONGRUENCIA
Dos o más figuras son congruentes ( ≅ ) si se cumple que son exactamente iguales tanto en forma como
en tamaño.
∆ ABC ≅ ∆ DEF
AB ≅ DE
BC ≅ EF
F
γ
γ
CA ≅ FD
A
29.
C
a
b
B
D
a
b
E
SEMEJANZA
Dos o más figuras son semejantes ( ~ ) si tienen igual forma pero no necesariamente el mismo tamaño. Sus
ángulos respectivos son congruentes y sus lados homólogos son proporcionales.
C
∆ ABC ~ ∆ DEF
DE = k
AB
EF = k
BC
γ
b
FD = k
CA
( k : razón de semejanza )
F
γ
a
b· k
h
A
a
c
a· k
h· k
b
B
D
a
c· k
b
E
a. Razón de semejanza
2
Los segmentos homólogos están en la misma razón ( k ) que sus perímetros y elementos secundarios. De la
figura, se cumple:
_Perímetro T DEFi a $ k
=
= b$k = c$k = h$k = k
b
c
h
_Perímetro T ABCi a
2
Las áreas están en una razón equivalente al cuadrado de la razón ( k 2 ). De la figura, se cumple:
_Área T DEFi 2
=k
_Área T ABCi
24
Editorial Moraleja
b. Homotecia
Una homotecia consiste en una ampliación o reducción, resultando una figura semejante a la original.
2
Si k > 1 , entonces La figura resultante es
más grande que la original.
2
Si 0 < k < 1 , la figura resultante es más
pequeña que la original.
OA’ > OA $ A’B’ > AB
OA’ < OA $ A’B’ < AB
C`
C
D
D`
B
B`
D
D’
C
B’
B
O
O
A’
A`
A
2
C’
Si –1 < k < 0 , la figura resultante esta al
otro lado del centro de homotecia y es
más pequeña que la original.
2
A
Si k < –1 , la figura resultante esta al otro
lado del centro de homotecia y es más
grande que la original.
OA’ > OA $ A’B’ > AB
OA’ < OA $ A’B’ < AB
A’
C
D
A’
C
D
B
O
B
B’
O
B’
D’
C’
A
D’
C’
A
Gráficamente otras relaciones de la homotecia son:
A’B’ = AB· k
$
A'B' = k
AB
$
B'C' = k
BC
C’D’ = CD· k
$
C'D' = k
CD
D’A’ = DA· k
$
D'A' = k
DA
B’C’ = BC· k
D`
c· k
C`
b· k
D
d
O
A
c
C
b
B`
d· k
B
a· k
a
A`
Propiedades
2
Siempre se cumple que todos los puntos de la figura resultante están alineados con respecto a el centro
de homotecia (O) y el punto correspondiente de la figura original.
2
Una homotecia con razón –1 es igual que una rotación de 180º de la figura con respecto al centro de
homotecia.
2
En el caso de polígonos, la figura resultante tiene sus lados paralelos a la figura original.
Editorial Moraleja
25
30.
PROPORCIÓN EN TRIÁNGULOS
a. Teorema de la bisectriz
2
Bisectriz interior
2
Bisectriz exterior
D
C
C
a
a
aa
A
B
P
Si CP bisectriz de ∢ ACB , se cumple:
A
AC
AP
=
BC
BP
B
P
Si CP bisectriz de ∢ BCD , se cumple: AC = PA
CB
PB
b. Teorema de Thales
Caso 1:
Si se cumple: AD // BE // CF
A
Caso 2:
Caso 3:
Si se cumple: AC // BD
Si se cumple: AD // BC
O
D
B
A
E
F
C
O
D
A
Entonces: OA = OC
AB
CD
Entonces:
B
Entonces: AB = DE = AC
BC
EF
DF
B
C
C
D
CO
BO
BC
=
=
OD
OA
AD
OA
OC
AC
=
=
OB
OD
BD
31.
POLÍGONOS
i. Propiedades de polígonos de n lados
2 Suma de los ángulos interiores:
2 Suma de ángulos exteriores:
180º· (n – 2)
360º
2 Diagonales desde un vértice:
n–3
n ^n – 3h
2
2 Total de diagonales:
ii. Polígonos Regulares
Son aquellos que tienen sus lados y sus ángulos respectivamente congruentes.
IMPORTANTE:
» Al trazar las diagonales en cualquier polígono
regular, éstas dividen al ángulo interior en partes
iguales. Ejemplo: Pentágono regular
» En un hexágono regular, las diagonales son
bisectrices de los ángulos interiores, y éstas
dividen al hexágono en 6 triángulos equiláteros
congruentes.
60º 60º
60º
60º
60º
60º
36°36°
36°
26
Editorial Moraleja
60º
60º
60º
60º
60º
60º
32.
PARALELÓGRAMOS
a. Propiedades comunes
2
Los ángulos opuestos son congruentes.
∢A = ∢C
2
; ∢B = ∢D
B
γ
b a
∢A + ∢B = ∢B + ∢C = 180º
∢C + ∢D = ∢D + ∢A = 180º
2
a
A
Los ángulos consecutivos son suplementarios.
d
P
b
Los lados opuestos son congruentes
b
AB = CD ; AD = BC
d
2
Las diagonales de un paralelógramo se dimidian.
AP = PC
2
;
γ
a
a
D
BP = PD
b
C
Las diagonales lo dividen en 4 triángulos de igual
área.
b. Clasificación de paralelogramos
i. Cuadrado
ii. Rectángulo
a
b
45º
45º
45º
45º
a
45º
45º
a
a
a
45º
45º
b
a
Características:
Características:
2
Diagonales perpendiculares
2
Diagonales bisectrices
2
Diagonales de igual medida
Perímetro:
4· a
Área:
a2
ó
2
^Diagonal h 2
2
iii. Rombo
Diagonales de igual medida
Perímetro:
2a + 2b
Área:
a· b
iv. Romboide
a
a
a
a
b
a
a
bb
a
a
b
h
b
Diagonales perpendiculares
2
Diagonales bisectrices
a· h ó
a
Características:
2
Área:
a
b
Características:
Perímetro: 4· a
h
^Diag 1 $ Diag 2 h
2
2
Solo las comunes a todo paralelógramo
Perímetro:
2a + 2b
Área:
b· h
Editorial Moraleja
27
33.
TRAPECIO
Trapecio es aquel cuadrilátero que tiene sólo
un par de lados paralelos, llamados bases. Sus
ángulos colaterales internos entre las bases son
suplementarios. Es decir, en la figura:
a + d = 180º
;
a
h
34.
b
a
A
B
b
AM = MD y BN = NC
Perímetro:
La medida de la mediana corresponde al
promedio de las bases.
MN =
c
N
M
b + γ = 180º
;
C
γ
d
La mediana (MN) es la unión de los puntos
medios de los lados no paralelos. Esta es paralela
a las bases.
AB // CD // MN
d
D
Área:
a+b+c+d
MN· h
AB + CD
2
TRAPEZOIDE
Trapezoide es aquel cuadrilátero que no tiene par de lados paralelos. Los trapezoides se clasifican en
asimétricos y simétricos.
Trapezoide simétrico (deltoide)
D
2
Una de las diagonales cumple la función de base (AC) y la otra
diagonal cumple la función de eje de simetría (BD).
2
Las diagonales son perpendiculares entre sí (AC ⊥ BD)
2
La diagonal, BD, divide al deltoide en dos triángulos congruentes.
2
La diagonal, AC, divide al deltoide en dos triángulos isósceles, cada
uno de base AC.
AC $ BD
Área deltoide:
2
2
A
C
B
35.
CIRCUNFERENCIA
a. Ángulos en la Circunferencia
i. De centro
ii. Inscrito
iii. Semi-inscrito
E
A
A
a
a
C
B
B
2b
A
b
a
b
2γ
O
iv. Relación entre
ángulos inscritos
T
γ
C
D
D
%
AB = a
28
Editorial Moraleja
%
DE = 2· γ
$
TA = 2· b
a=b
v. Inscrito en una
semi-circunferencia
vi. Relación entre
ángulos inscritos y
de centro
vii. Cuadrilátero
inscrito
A
B
C
A
a
A
O
O
•
2a
b
B
a
O
•
B
2a
D
a
B
C
a+γ = b+d =
Si, AB // CD ,
entonces,
& %
DA = BC
xi. Tangentes desde un xii. Triángulo isósceles
punto
de radio r
A
2a
P
a C
O•
bO
a
∢ BAO = ∢ OBA
a + b = 180º
xiv.
∆ ABO, isósceles de
base AB
Ángulo Exterior
B
C
C
a
b
A
D
A
D
% &
AB + CD
2
B
A
B
a=
a
a
B
entonces,
%
&
AB = CD = 2a
a
r
r
Si AB = CD = m ,
xiii.Ángulo Interior
a=γ
180º
m
a
γ
C
D
D
m
C
D
x. Cuerdas Iguales
A
a
d
C
A
B
A
γ
a=b+γ
ix. Rectas paralelas
a
b
γ
B
∢ ACB = 90º
viii. Exterior en un
cuadrilátero
b=
% &
AB - CD
2
Editorial Moraleja
29
b. Proporciones en la Circunferencia
i. Teorema de las secantes
ii. Teorema tangentesecante
iii. Teorema de las cuerdas
C
B
C
D
A
P
E
A
•
P
B
O
A
T
B
D
PT 2 = PA· PB
PA· PB = PD· PC
iv. Caso particular de las
cuerdas
AE· EB = CE· ED
v. Tangentes desde un
punto
vi. Cuadrilátero circunscrito
a una circunferencia
A
B
C
A
O
E
A
O
P
C
B
D
D
B
Si AB ⊥ CD, entonces:
PA = PB
CE = DE , CE 2 = AE· EB
AB + CD = BC + AD
c. Áreas y Perímetro
i. Círculo
ii. Sector circular
O
•
O
•
a
r
r
P
Área:
Perímetro:
30
A9 = r $ r2
P9 = 2 $ r $ r
Editorial Moraleja
r
B
A
Área SC:
Perímetro SC:
AS 9 = r $ r2 $
a
360º
P S9 = 2 $ r $ r $
a
+ 2r
360º
36.
SISTEMA CARTESIANO
a. Distancia entre puntos, punto medio y pendiente
i. Distancia entre puntos
d AB
y
= ^x 2 – x 1 h2 + ^y 2 – y 1 h2
ii. Punto medio de un segmento
M
ym
y1 + y2
x + x2
Xm = 1
; ym =
2
2
iii. Pendiente:
B
y2
y2 – y1
A
y1
x2 – x1
y2 – y1
m = x2 – x1
0
x1
xm
x
x2
b. Relación entre el ángulo de inclinación y pendiente de la recta
Sea a el ángulo de inclinación y m la pendiente de la recta R. Entonces:
Si, m = 0
Si, m > 0
Si, m < 0
→ a = 0º
→ 0º < a < 90º
→ 90º < a < 180º
y
y
y
y
R
a
x
R
R
R
37.
Si, m = ∞
→ a = 90º
x
a
x
x
ECUACIÓN DE LA RECTA
Forma principal: y = mx + n
y
2
m: Pendiente
2
n: Coeficiente de posición. Valor donde la recta corta al eje y.
–n : Valor donde la recta corta al eje x
m
2
n
–
Forma general: ax + by = c
x
n
m
a. Hallando la ecuación de la recta
Para hallar la ecuación de la recta, dependiendo la información que nos den, podemos usar alguno de
los siguientes métodos:
2
2
Punto y pendiente : y – y1 = m· ( x – x1 )
x y
Intersección ejes: a + = 1 . (a: valor donde corta al eje x y b: valor donde corta al eje y).
b
b. Rectas paralelas y perpendiculares
Sean R1 y R2 rectas de pendientes m1 , m2 y coeficiente de posición n1 , n2 respectivamente. Entonces:
2
Rectas paralelas
R2
2
Rectas perpendiculares
y
y
R1
R2
R1
a
a
R1 // R2 si y solo si m1 = m2
x
x
R1 ⊥ R2 rectas de pendientes m1· m2 = –1
Editorial Moraleja
31
38.
GEOMETRÍA DEL ESPACIO
Medida de un segmento en el espacio
Sean los puntos A( a , b , c ) y B( m , n , p).
Para encontrar la distancia entre ellos, utilizamos la fórmula: D = ^a - m h 2 + ^b - n h 2 + ^c - p h 2
39.
VECTORES
a. Operatoria con vectores
a = ( ax , ay ) , b = ( bx , by ) y c = ( cx , cy ), se cumple:
Adición y sustracción
2
2
Y
Y
C
ay + by
ay
ax
bx
x
x
ax + bx
X
Ponderación por un escalar
2
Si k > 0, se mantiene el sentido pero
cambia la magnitud.
2
Si k < 0, cambia tanto la magnitud como
el sentido del vector.
X
cx
ax
AC = _ c x – a x , c y – a y i
Y
A`
k· ay
A
ay
a
O
ax
k· ax
X
Módulo o Magnitud de un vector
a = a = ^a xh2 + ^a yh2
ECUACIÓN VECTORIAL DE LA RECTA
Supongamos una recta R que pasa por el punto A y
O. Esta posee una dirección dada por el vector d .
Sean a y p los vectores de posición de los puntos
respectivos. De la figura podemos observar que la
suma de los vectores a + AP = p .
Del vector AP , solo conoceremos su dirección
(pendiente), ya que su magnitud variara infinitas
veces, es por esto que el vector AP se representa
como el vector dirección multiplicado por un
escalar, el que comunmente se designa por la letra
l _ AP = l d i
.
Ahora la suma anterior queda escrita como:
p = a + AP
32
O
, a !b k
y
y
El sentido y módulo varían de acuerdo al
valor del escalar.
40.
c
a
k $ a = k $_ ax ,ay i
=a
k $ ax ,k $ ay k
2
AC
A
ay
B
a! b =a
a !b
2
C
cy
A
by
O
Vectores no anclados en el origen
→
Editorial Moraleja
p = a + ld
y
R
A
•
d
P
a
•
p
•
O
x
i. Ecuación vectorial con
coordenadas:
ii. Ecuación paramétrica:
^x , yh = ^a x , a yh + l _ d x , d y i
iii. Ecuación simétrica de la
recta:
x – ax y – ay
=
dx
dy
x = a x + ld x
y = a y + ld y
Rectas paralelas y perpendiculares
y R2(l) = q + l· s . Las las rectas R1(l)
Si tenemos dos rectas escritas en forma vectorial: R1(l) = p + l· d
y R2 (l) serán:
41.
i.
Paralelas si: d = k $ s , con k ! R – {0}
ii.
Perpendiculares si: d x $ s x + d y $ s y = 0
TRANSFORMACIONES ISOMÉTRICAS
Las transformaciones isométricas son: traslación, rotación, simetría central y simetría axial.
a. Traslación
Para trasladar un punto o figura, se necesita un vector
traslación. Para obtener la posición de un punto trasladado
en el plano cartesiano, se debe sumar las coordenadas
del punto inicial (x , y) más las coordenadas del vector
traslación (u , v).
y
5
En caso de tener las coordenadas del punto inicial y final, y
necesitar el vector traslación, este se encuentra restando
las coordenadas del punto final menos el inicial, en ese
orden. Ejemplo en la figura adjunta.
A (4 , 5)
T ( 4 , –3 )
A’ ( 8 , 2 )
2
4
8
x
b. Rotación
Para rotar un punto o figura, se necesita un centro de rotación (punto en torno al cual se gira), un ángulo de
rotación (indica cuánto se gira).
i. Rotaciones en torno al origen
Si rotamos el punto ( x , y ) con respecto al origen
O( 0 , 0 ) en un ángulo de giro de 90º, 180º, 270º
ó 360º, las coordenadas de los puntos obtenidos
están dados en la siguiente tabla:
Inicial
(x , y)
90º
180º
270º
( –y , x ) ( –x , –y ) ( y , –x )
360º
(x , y)
ii. Rotaciones en torno a un punto distinto al origen
En caso que el centro de rotación no sea el origen, el proceso para realizar la rotación es:
2 1ro, encontrar el vector traslación que lleva el centro de rotación (C) hacia el punto a rotar (A) (vector
CA = A – C ).
2 2do, aplicar al vector resultante ( CA ) la rotación requerida, utilizando la tabla anterior.
2 3 ro, sumar al centro de rotación, el vector obtenido en el paso 2.
c. Simetrías central
En una simetría central, un punto o figura es reflejada con respecto a otro punto llamado centro de simetría.
En una simetría central se cumple:
2 Los trazos de la figura original son paralelos a los trazos homólogos de la figura transformada.
2 Los puntos homólogos están a la misma distancia del centro de simetría.
2 Una simetría respecto de un punto O equivale a una rotación en 180º de centro O.
2 Todo punto del plano cartesiano ( x , y ) tiene su simétrico con respecto al origen al punto ( –x , –y )
Editorial Moraleja
33
i. Figuras con centro de simetría
Se dice que una figura tiene centro de simetría, si existe un punto por el cual, si se rota la figura en 180º, la
figura resultante coincide con la figura original. Ejemplo: Circulo, cuadrado, hexágono regular, etc.
d. Simetría axial
En una simetría axial, un punto o una figura es reflejada con respecto a una recta, llamada eje de simetría,
formándose un efecto espejo. En una simetría axial se cumple:
2 Los puntos homólogos quedarán a la misma distancia del eje de simetría.
2 El segmento que uno los puntos homólogos, es perpendicular al eje de simetría.
2 Todo punto del plano cartesiano A( x , y ) tiene un simétrico A’( x , –y ) con respecto al eje de las abscisas
(eje x) y un simétrico A”( –x , y ) con respecto al eje de las ordenadas (eje y).
i. Figuras con eje de simetría
Podemos entender el eje de simetría en base a la siguiente idea: si doblamos una figura respecto a una
línea, y las dos mitades coinciden, en ese caso esa línea corresponde al eje de simetría.
42.
CUERPOS
i. Cubo
ii. Paralelepípedo
d
a
iii. Prisma
d
iv. Pirámides
h
c
h
a
b
a
a
Base
2
Área: 6 · a
2
2
Volumen: a3
2
Diag. (d) : a·
2
Área:
2
Suma de áreas
laterales
y
basales
3
2
Área:
2
Suma de áreas
laterales y basales
2
Volumen:
Suma de áreas
laterales y basales
Volumen:
2
Área basal · h
(a· b· c)
2
Área:
Volumen:
1
· Área basal · h
3
Diag:
a2 + b2 + c2
v. Cilindros
vi. Conos
g
h
r
h
r
2
2
34
vii. Esferas
r
2
Área: 2· p· r + 2· p· r· h
2
G e n e r a t r i z :
g = ^ r h 2 + ^hh 2
2
Área:
2
Volumen:
2
Volumen: p· r · h
Editorial Moraleja
r $ r $ g + r $ r2
1
· p· r 2· h
3
4 $ r $ r2
2
Área:
2
Volumen:
4
$ r $ r3
3
43.
PERMUTACIÓN, VARIACIÓN Y COMBINACIÓN
PR nr =
P9 = ^ n – 1 h !
n!
a! $ b! $ ... $ r!
¿Es
circular?
P n = n!
44.
SI
SI
¿Se repite
algún
elemento?
SI
SI
¿Se usan
todos los
elementos?
NO
SI
NO
V nr =
NO
¿Importa el
orden de los
elementos?
NO
VR nr = n r
¿Se repite
algún
elemento?
SI
n
CR r =
¿Se repite
algún
elemento?
n
Cr =
NO
NO
n!
^n – r h !
^n + r – 1h !
^n – 1 h ! $ r!
n!
^n – r h ! $ r!
PROBABILIDADES
a. Probabilidad clásica o regla de Laplace
En un experimento aleatorio, la probabilidad de un suceso A se obtiene dividiendo el número de casos
favorables al evento A por el número total de casos posibles (espacio muestral).
Nº de casos favorables (A)
P (A) =
Nº total de casos
b. Ley de los grandes números
La ley de los grandes números establece que a medida que la cantidad de veces que se realiza un
experimento aleatorio aumenta, la frecuencia relativa de un suceso tiende a un determinado valor, el cual
es el valor teórico de su probabilidad.
c. Probabilidades de eventos
i. Eventos excluyentes
Sean A y B, dos eventos excluyentes (NO pueden ocurrir ambos al mismo tiempo) de un espacio muestral
E. La probabilidad de que ocurra A o B esta dada por:
P(A o B) = P (A ∪ B) = P(A) + P(B)
Ejemplo:
Gráficamente
Sean los conjuntos: E = { 1 , 2 , 3 , 4 , 5 , 6 } , A = { 3 , 5 } , B = { 2 , 4 , 6 }.
¿Cuál es la probabilidad de que ocurra A ó B.
E
P(A o B) = P (A ∪ B) = P(A) + P(B)
= 2 + 3 = 5
6
6
6
2
A
B
4
3
5
6
1
Editorial Moraleja
35
ii. Eventos NO excluyentes
Sean A y B, dos eventos no excluyentes (pueden ocurrir ambos al mismo tiempo) de un espacio muestral
E. La probabilidad de que ocurra A o B esta dada por:
P(A o B) = P (A ∪ B) = P(A) + P(B) – P (A ∩ B)
Ejemplo: Sean los conjuntos: E = { 1 , 2 , 3 , 4 , 5 , 6 } , A = { 2 , 3 , 5 } , B = {
2 , 4 , 6 }. Cual es la probabilidad de que ocurra A ó B.
Gráficamente:
E
A
P(A o B) = P (A ∪ B) = P(A) + P(B) – P (A ∩ B)
= 3 + 3 – 1 = 5
6
6
6
6
B
4
2
3
5
6
1
iii. Sucesos independientes
Se A y B, dos sucesos independientes de (La ocurrencia de uno no influye sobre la ocurrencia del otro) de
un espacio muestral E. La probabilidad de que ocurra A y B esta dada por:
P(A y B) = P (A ∩ B) = P(A)· P(B)
Ejemplo: Sean el espacio muestral: E = { 1 , 2 , 3 , 4 , 5 , 6}. ¿Cuál es la
probabilidad de sacar un número que sea par y múltiplo de 3?.
Gráficamente.
E
Múltiplos de 3: A = { 3 , 6 } . Pares: B = { 2 , 4 , 6 }
P( x3 y par ) = P ( x3 ∩ par ) = P( x3 )· P(par)
= 2 · 3
=
6
6
A
3
1
6
6
B
2
5
4
1
iv. Sucesos dependientes
Sean A y B, dos sucesos dependientes (de un mismo espacio muestral E, por lo tanto, la ocurrencia de uno
influye sobre la ocurrencia del otro, modificándose el espacio muestral). La probabilidad de que ocurra A
cuando B ya ha ocurrido esta dada por:
P^A + Bh
P ^A/B h =
P^Bh
Ejemplo: Sean el espacio muestral: E = { 1 , 2 , 3 , 4 , 5 , 6}. ¿Cuál es la
probabilidad de que al sacar un número este sea múltiplo de 3, dado
que sacamos un número par?.
Múltiplos de 3: A = { 3 , 6 }. Pares: B = { 2 , 4 , 6 }. P ( A ∩ B) = 1 . P ( B) = 3
6
6
1
P^A + Bh
P^A + Bh
P ^A/B h =
= 6 = 6 = 1
= P ^A/B h =
3
18
P^Bh
P^Bh
3
6
45.
Gráficamente esto es:
E
A
3
6
B
2
5
4
1
FUNCIÓN DE PROBABILIDAD
Se llama función de probabilidad, f(x), de una variable aleatoria discreta “X” a la aplicación que asocia a
cada valor de x i de la variable su probabilidad p i . Se denota por f(x) = P( X = x i )
Propiedades:
36
0 ≤ f( x i ) ≤ 1
Editorial Moraleja
;
f( x 1 ) + f( x 2 ) + … + f( x n ) = 1
a. Función de distribución de probabilidad
La función de distribución de probabilidad, F(x), asocia a cada valor de x la probabilidad acumulada, es
decir F(x) = P(X ≤ x)
i. Propiedades
2 0 ≤ F(x) ≤ 1
2 Si a < b, entonces P( a < x ≤ b ) = F (b) – F (a)
2 P( X > a ) = 1 – P( X ≤ a ) = 1 – F(a)
En el caso de variable aleatoria discreta la
función de distribución de probabilidad es una
función escalonada, donde el máximo valor
que toma F(x) = 1
En el caso de variable aleatoria continua la
función de distribución de probabilidad es una
función continua, y la probabilidad de que
la variable esté comprendida en el intervalo
[ a , b ] está dada por el área bajo la curva de
la función entre los puntos a y b.
f(x)
y
f(x)
1
P (a < x < b)
Valores v.a.
discreta
46.
a
b
x
ESPERANZA DE UNA VARIABLE ALEATORIA DISCRETA
La esperanza de una variable aleatoria discreta, E( x ), se determina por la suma de los productos de la
probabilidad de cada suceso multiplicada por el valor de dicho evento. Si x i y pi , corresponden a el valor
del suceso i y la probabilidad que la variable tome el valor i, respectivamente, entonces se define a la
esperanza como:
E(x) = x1· p1 + x 2· p2 + x3· p3 + ... + xn· pn
Aplicaciones de la esperanza
La esperanza aplicada en los juegos de azar y hace relación a la esperanza que tenía de ganar un juego
un individuo que hacía un gran número de apuestas.
2 Si E(X) = 0 el juego es equitativo, es decir se considera justo
2 Si E(X) > 0 el juego se considera favorable
2 Si E(X) < 0 el juego se considera injusto.
47. TRIÁNGULO DE PASCAL
El triángulo de Pascal se utiliza en experimentos aleatorios que tengan dos sucesos equiprobables de
ocurrencia, como por ejemplo: lanzar una moneda, el sexo de una persona, respuestas de preguntas del
tipo Cara o Sello, etc. Gráficamente se muestra en la figura siguiente:
1S1
2 C1 S1
1S2
1C3
3 C2 S1
3 C1 S2
1S3
4 C3 S1
6 C2 S2
4 C1 S3
1S4
5 C4 S1
10 C3 S2
10 C2 S3
5 C1 S4
1C2
1C5
1C4
1C1
1S5
=2
=4
=8
= 16
= 32
2 Los coeficientes primero y último de cada fila son siempre 1
2 Cualquier otro coeficiente de una fila se obtiene como la suma de los dos valores que están justo arriba
en la fila anterior.
2 Si se suman los números de cada fila el resultado es siempre una potencia de 2.
2 Existe una simetría en cada fila respecto a su centro.
Editorial Moraleja
37
48.
DISTRIBUCIÓN BINOMIAL
a. Función de probabilidad binomial
La distribución binomial se representa por B( n , p ), siendo n el número de pruebas o repeticiones del
experimento, p es la probabilidad de éxito, (1 – p) la probabilidad de fracaso y x el valor de la variable X.
n
P(X = x) = d n
· p x· ( 1 – p ) n – x
x
n
n
n!
= Cx =
Recordar que: d n
_n – xi
x
! $ x!
b. Función de distribución acumulada de la distribución binomial
n
n
n
P ( X ≤ xi ) = d n
· p 0· ( 1 – p ) n – 0 + d n
· p 1· ( 1 – p ) n – 1 + ... + f p
· p x i· ( 1 – p ) n – x i
xi
0
1
c. Esperanza y varianza de la distribución binomial
E(X) = n· p
49.
;
Var (X) = n· p· ( 1 – p )
MEDIDAS DE TENDENCIA CENTRAL
Las medidas de tendencia central son indicadores que representan valores numéricos en torno a los cuales
tienden a agruparse los valores de una variable estadística. Los principales son la media aritmética, la
mediana y la moda.
i. Moda:
Es el dato que aparece con mayor frecuencia, es decir, el que más se repite.
ii. Mediana:
Es el dato que ocupa la posición central de la muestra cuando estos se encuentran ordenados en forma
creciente o decreciente. Si la muestra tiene un número par de datos, la mediana es la media aritmética
de los dos términos centrales.
iii. Media Aritmética (X):
La media aritmética o promedio, es el cuociente entre la suma de todos los datos y el número de datos. Si
se tienen n datos; x1 , x 2 , x3 , ... , xn, su media aritmética e
x + x 2 + x 3 + ... + x n
X= 1
n
iv. Media Aritmética para datos organizados en una tabla de frecuencias
La media aritmética o promedio para datos ordenados en tabla es el resultado de la multiplicación de
los datos por sus frecuencias, dividido por la cantidad de datos. Si se tienen n datos; x1 , x 2 , x3 , ... , xn, y sus
respectivas frecuencias f1 , f2 , f3 , ... , fn, entonces la media aritmética es
X=
38
Editorial Moraleja
x $ f + x $ f + x $ f + ... + x n $ fn
1 1
2 2
3 3
f1 + f2 + f3 + ... + fn
50.
MEDIDAS DE DISPERSIÓN
i. Desviación estándar
Es una medida de dispersión y nos indica cuánto tienden a alejarse los datos del promedio aritmético.
Para calcular la desviación estándar (s) se utilizan las siguientes fórmula:
Para datos no agrupados:
Para datos agrupados:
` x 1 – x j + ` x 2 – x j + ... + ` x n – x j
n
2
2
s=
2
f1 $ ` x 1 – x j + f2 $ ` x 2 – x j + ... + fn $ ` x n – x j
2
2
s=
2
f1 + f2 + ... + fn
Propiedades de la desviación estándar
Sea x una variable aleatoria y k un número real
2
s (x) ≥ 0
s (k) = 0
2
2
s (x + k) = s (x)
2
s (kx) = k· s (x)
ii. Varianza
Es otra medida de dispersión que corresponde al cuadrado de la desviación estándar. Var (x) = s 2.
Sea x una variable aleatoria y k un número real, se cumple:
2
51.
Var (x) ≥ 0
Var (k) = 0
2
2
Var (x + k) = Var (x)
2
Var (kx) = k 2 · Var(x)
MEDIDAS DE POSICIÓN
i. Cuartiles
Son los tres valores que dividen a un conjunto ordenado de datos en cuatro partes iguales. Q1, Q2 y Q3
determinan los valores correspondientes al 25%, 50% y 75% de los datos, respectivamente.
ii. Percentiles
Son los valores que dividen a un conjunto ordenado de datos en 100 partes iguales. El percentil de orden K
se denota por PK, y en el caso discreto es la observación cuya frecuencia absoluta acumulada alcanza el
valor igual al K% de las observaciones.
52.
DISTRIBUCIÓN NORMAL
El gráfico de la función de densidad de una variable aleatoria
con distribución normal recibe el nombre de campana de Gauss,
en la figura adjunta. Esta distribución queda definida por dos
parámetros: la media (m) y la desviación estándar (s), y se denota
X ~ N( m ; s ).
–∞
+∞
m
iii. Propiedades de la distribución Normal
2 El área bajo la curva es igual a la unidad
2 Es simétrica con respecto a x = m. La función queda dividida en dos con una probabilidad del 50% de
observar un dato mayor a la media y un 50% de observar un dato menor a la media.
2 Es asintótica al eje de las abscisas.
2 La media, moda y mediana coinciden.
a. Distribución normal estándar
La distribución normal estándar es aquella que tiene media 0 y desviación estándar 1. X ~ N(0 ; 1)
Para calcular la probabilidad en distribuciones normales podemos usar tablas que presentan las áreas bajo
las curvas y que permiten determinar la probabilidad en ese intervalo. Para efectos de este texto y de la PSU
ocuparemos la tabla con las probabilidades más utilizadas. La tabla a utilizar es:
z
0,67
0,99
1,00
1,15
1,28
1,64
1,96
2,00
2,17
2,32
2,58
P(Z ≤ z)
0,749
0,839
0,841
0,875
0,900
0,950
0,975
0,977
0,985
0,990
0,995
Editorial Moraleja
39
i. Propiedades
P (X ≤ x1)
P (X ≥ x1) = 1 – P (X ≤ x1)
x1
∞
∞
∞
x1
P (X ≤ –x1) = P (X ≥ x1)
∞
∞
–x1
x1
∞
ii. Estandarizar
Para efectos prácticos a una variable aleatoria X con distribución normal N( m , s ) , debemos estandarizar
los datos para que la variable distribuya normal N(0 , 1). Para normalizar, debemos a nuestra variable x,
X–n
restarle la media y dividirla por la desviación estándar. Esto es: Z = v
Entonces la probabilidad en términos de la variable X puede calcularse en términos de Z, utilizando las
tablas de distribución tipificada, es decir:
x –n
P_ X # x i
= Pb Z # v l
b. Aproximación de la probabilidad binomial por la probabilidad de la normal
La distribución binomial escrita como : X ⤳ B(n, p).(Donde n: numero experimentos; p, probabilidad de
exito) .
Al aumentar la cantidad de repeticiones la distribución binomial se acerca cada vez más a una distribución
normal con media: m =n· p y desviación estándar: s = np ^ 1– p h
53.
INTERVALOS DE CONFIANZA
Un intervalo de confianza es un rango de valores que probablemente contiene el valor del parámetro que
se quiere estimar (típicamente la media poblacional), dada cierta probabilidad de éxito.
El nivel de confianza es la probabilidad de que el intervalo calculado contenga al verdadero valor del
parámetro y se determina por ( 1 – a ), siendo a el nivel de significación. Los niveles de confianza más usuales
son: 90%, 95% y 99%, que corresponden a niveles de significación de 10%, 5% y 1%, respectivamente.
Los limites de confiabilidad son los valores que establecen los límites del intervalo de confianza.
Así para determinar un intervalo de confianza para la media poblacional m, de una muestra de tamaño n,
que sigue una distribución normal, con un nivel de confianza de (1– a), con s conocida se calcula como:
v
v
IC : <
X – Za $
; X +Za $
F
e
e
n
n
2o
2o
El margen de error es: Z a $
e
o
2
54.
s
n
RELACIÓN ENTRE LA MEDIA POBLACIONAL Y LA MEDIA MUESTRAL
La media de una población, m, se puede estimar a partir de la media de muestral, X. El error muestral, e, se
define como la diferencia entre la media poblacional y la media muestral:
ei = m – X
NOTAS:
» El error muestral puede ser tanto positivo como negativo.
» La suma de todos los errores muestrales es cero.
» A medida que el tamaño de la muestra crece, el error tiende a disminuir, ya que el tamaño de la muestra
se acerca al tamaño de la población.
40
Editorial Moraleja
Tabla de conversión de puntajes - Admisión 2017
Correctas
Puntaje
Correctas
Puntaje
Correctas
Puntaje
1
160
26
521
51
630
2
170
27
527
52
635
3
180
28
532
53
639
4
190
29
538
54
644
5
200
30
542
55
648
6
210
31
548
56
653
7
232
32
552
57
658
8
255
33
557
58
663
9
279
34
561
59
668
10
304
35
565
60
673
11
326
36
570
61
679
12
349
37
573
62
685
13
370
38
578
63
691
14
389
39
582
64
697
15
407
40
585
65
704
16
425
41
590
66
712
17
439
42
594
67
719
18
453
43
597
68
728
19
465
44
602
69
737
20
476
45
605
70
756
21
486
46
609
71
775
22
494
47
614
72
794
23
502
48
617
73
812
24
509
49
622
74
831
25
516
50
626
75
850
Para el cálculo de las cantidad de preguntas correctas, no considerar las marcadas como piloto.
Editorial Moraleja
41