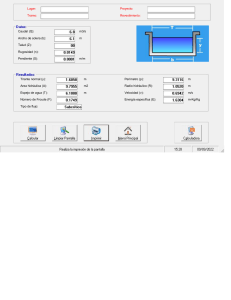
-SECCIONES DE MAYOR EFICIENCIA HIDRAULICADEFINICION: Uno de los factores que intervienen en el costo de construcción de un canal es el volumen por excavar; este a su vez depende de la sección transversal. Mediante ecuaciones se puede plantear y resolver el problema de encontrar la menor excavación para conducir un caudal dado, conocida la pendiente. La forma que conviene dar a una sección de magnitud dada, para que escurra el mayor caudal posible, es lo que se ha llamado “sección de máxima eficiencia hidráulica”. En términos simples, la sección de Máxima Eficiencia Hidráulica es aquella para la cual se obtiene un área mojada mínima para transportar determinado caudal, con rugosidad, pendiente y forma geométrica especificada. La sección de máximo rendimiento para un canal abierto se define como aquella sección que dé el máximo caudal cuando se dan la pendiente, el área y el coeficiente de rugosidad. Si estas magnitudes se mantienen constantes, la velocidad (y, por tanto, el caudal) será máxima cuando el perímetro mojado sea mínimo. Basándose en esta premisa, se puede determinar la sección de mayor rendimiento (y, por lo tanto, la más económica) para las formas más comunes. CONCEPTO: El trazado horizontal del canal deberá ser tal que garantice que su pendiente longitudinal sea paralela a la del terreno, lo cual se logrará en terrenos de Topografía muy uniforme. Si éste es el caso, y especialmente en el caso de canales revestidos, la recomendación es que se utilice el criterio de la Sección de Máxima Eficiencia, pues es la que por lo general resulta como la más económica en este tipo de topografía: menor excavación y menor recubrimiento. 1 Cuando la topografía es muy irregular, de seguro aparecerán profundidades para la rasante del canal que estarán asociadas a sobre-excavaciones que son indeseables en todo caso. En estas condiciones ya el criterio de máxima eficiencia hidráulica no estará asociado a la economía, siendo entonces recomendable utilizar secciones en las que el ancho de la base es menor que el correspondiente a la sección de máxima eficiencia. De esta forma, al prevalecer una sección más angosta, el volumen de sobre-excavación se verá reducido. De esta forma, antes de iniciar el proceso de diseño es conveniente que hayamos considerado estos aspectos, especialmente en lo que respecta a si utilizaremos canales revestidos o no, generalmente los primeros suelen requerir de una inversión inicial elevada, pero a mediano y largo plazo el costo de mantenimiento justifica su selección. RETOMANDO LO SUBRAYADO DE LA DEFINICION: Mediante ecuaciones se puede plantear y resolver el problema de encontrar la menor excavación para conducir un caudal dado, conocida la pendiente. Normalmente para los problemas de canales hidráulicos los datos que nos dan son: Q, n, z, S, hay muchas combinaciones de las incógnitas “b” y “y” que satisfacen la fórmula de Manning. Existe el caso en que tanto el tirante normal y la base de la sección transversal son las incógnitas en estos casos puede buscarse la sección de máxima eficiencia hidráulica. 2 La sección de Máxima eficiencia hidráulica es aquella que para la misma área tiene el perímetro mínimo. En consecuencia la sección de máxima eficiencia hidráulica es la semicircular: Esto, basándose en la propiedad geométrica de ser el círculo la figura que para la misma área tiene el perímetro mínimo. En las condiciones normales la sección de Máxima Eficiencia Hidráulica involucra la mínima sección de excavación, de revestimiento y de superficie de infiltración. También debe tenerse en cuenta que el perímetro mínimo involucra menor rozamiento, sin embargo, los canales circulares son pocos usados. OBTENCION DE LA SECCION MAXIMA EFICIENCIA HIDRAULICA Lo primero que se debe tomar en cuenta es que lo que nos dará la sección de máxima eficiencia hidráulica es la geometría de la sección transversal de nuestro canal y las variables que nos dan la geometría son: b, y, z. 1.-) Sección rectangular. Dónde: z=0 Sea el área: 𝐴 = 𝑏𝑦 El perímetro será: 𝑃 = 𝑏 + 2𝑦 Sustituyendo b en P: 𝑃= 3 A y despejando b: + 2𝑦 𝑏= A y Derivando P con respecto a “y”, se deriva P porque en este caso queremos el valor mínimo de P ya que con esto conseguiremos un radio hidráulico máximo y por lo tanto un gasto máximo: 𝑑𝑃 =0 𝑑𝑦 𝑑𝑃 𝐴 [ + 2𝑦] = 0 𝑑𝑦 𝑦 𝐴 =2 𝑦2 𝐴 = 2𝑦 2 Si: 𝑏= 𝐴 𝑦 = 2𝑦 2 𝑦 𝑏 = 2𝑦 𝑏 =2 𝑦 Relación de (base-tirante) para máxima eficiencia hidráulica del rectángulo. Así se obtiene que el radio hidráulico máximo:𝑅 4 = A Pmin = 2𝑦 2 b+2y = 2𝑦 2 2y+2y = y 2 2.-) Sección trapecial. ky k Sea el área: 𝐴 = (𝑏 + 𝑘𝑦)𝑦 El perímetro será: 𝑃 𝐴 ; 𝑏 = − 𝑘𝑦 𝑦 = 𝑏 + 2𝑦√1 + 𝑘 2 Sustituyendo el valor de b en P: 𝑃= Por lo tanto: 𝑑𝑃 𝑑𝑦 =− Despejando el área: 𝐴 Si: 𝑏 𝐴 = − 𝑘𝑦 𝑦 Entonces: 𝐴 𝑦2 𝐴 − 𝑘𝑦 + 2𝑦√1 + 𝑘 2 𝑦 − 𝑘 + 2𝑦√1 + 𝑘 2 = 0 = [2√1 + 𝑘 2 − 𝑘]𝑦 2 𝑠𝑢𝑠𝑡𝑖𝑡𝑢𝑦𝑒𝑛𝑑𝑜 𝑒𝑛 𝑣𝑎𝑙𝑜𝑟 𝑑𝑒 𝐴 𝑒𝑛 𝑏: 𝑏 = 2𝑦(√1 + 𝑘 2 − 𝑘) 𝑏 𝑦 = 2(√1 + 𝑘 2 − 𝑘) Relación de (base-tirante) para máxima eficiencia hidráulica de la sección trapecial. Así se obtiene que el radio hidráulico máximo:𝑅 5 = A Pmin = [2√1+𝑘 2 −𝑘]𝑦 2 𝑏+2𝑦√1+𝑘 2 = y 2 Si el talud es variable se puede considerar lo siguiente. k talud 𝑏 𝑑/𝑦 0 2y 0.5 1.2361y 1 0.8284y 1.25 0.7016y 1.5 0.6056y 2 o más ~0y 2y 1.2361 0.8284 0.7016 0.6056 ~0 Formulas: 𝑏 𝑃 = 𝑦( + 2√1 + 𝑘 2 ) 𝑦 𝑏 = 2(√1 + 𝑘 2 − 𝑘) 𝑦 𝑃𝑚𝑖𝑛 = 4𝑦√1 + 𝑘 2 − 2𝑦𝑧 dPmin =0 dk De donde obtenemos el talud que dará la mayor eficiencia hidráulica. 𝑘= 6 √3 3 EJEMPLO DE MAYOR EFICIENCIA HIDRAULICA: Un canal debe transportar 6 𝑚3 /𝑠. La inclinación de las paredes (talud) impuesta por la naturaleza de terreno es de 60° con la horizontal. Determinar las dimensiones de la sección transversal con la condición de obtener máxima eficiencia hidráulica. La pendiente del fondo es de 0.003 y el coeficiente de rugosidad de Kutter se ha considerado de 0.025. Solución 1 con grafica.-) Datos: Q = 6 𝑚3 /𝑠 k = 60° S = 0.003 n = 0.025 Solución 1) 𝑡𝑔 60° = 1 1 = 1.732 𝑝𝑜𝑟 𝑙𝑜 𝑡𝑎𝑛𝑡𝑜 𝑘 = = 0.5774 𝑘 1.732 Tenemos que para la máxima eficiencia hidráulica: 𝑏 = 2(√1 + 𝑘 2 − 𝑘) 𝑦 𝑏 = 2 (√1 + 0.57742 − 0.5774) = 1.155 𝑦 Para usar la gráfica de Ven Te Chow necesitamos el valor obtenido anteriormente dando un valor de Así se puede obtener el valor de Pero además sabemos que 𝐴𝑅 7 2 3 𝐴𝑅 2/3 𝑏8/3 = 𝑦 para ello solo basta con invertir 𝑏 𝑦 𝑏 = 0.8661 = 0.74 𝑄𝑛 1 𝑆2 = (6)(0.025) 1 0.0032 = 2.74 Siendo así podemos ahora decir que: 𝐴𝑅 2/3 𝑏8/3 = 2.74 𝑏8/3 = 0.74 De donde 𝑏 = 1.63 : 𝑏 𝑏 1.63 = 1.155 ∶ 𝑦 = = = 1.41 𝑦 1.155 1.155 Conclusión: y = 1.41m A= (1.63+1.41*0.577)*1.41=3.44𝒎𝟐 V=1.74m/s R=0.705m Solución 2.-) También se puede usar la fórmula del área obtenida en los análisis anteriores: 𝐴 = [2√1 + 𝑘 2 − 𝑘]𝑦 2 área de la máxima eficiencia hidráulica y aplicando formulas conocidas: 𝐴 = 1.73𝑦 2 𝑡𝑎𝑛60 = 𝑜𝑝𝑢𝑒𝑠𝑡𝑜 𝑎𝑑𝑦𝑎𝑐𝑒𝑛𝑡𝑒 Aplicando la fórmula de Manning: 𝑦 𝑄 = 1.73𝑦 2 Si se sabe que 2 1 ( 2 )3 (0.003)2 0.025 1.41 𝑋 = 𝑋 = 0.814 Q = 6 𝑚3 /𝑠 Entonces se concluye que: Figura de conclusión. 8 8 = 2.39𝑦 3 𝑡𝑎𝑛60 = y = 1.41 √0.8142 + 1.412 = 1.63 Bibliografía: 9 Mecanica de fluidos (Edgar Sparrow Alamo) Mecanicxa de los fluidos e hidráulica (Ronald V.Giles, Jack B. Evett, Cheng Liu)