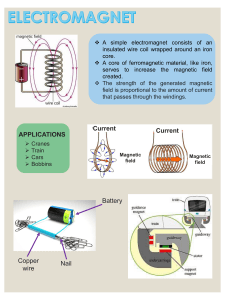
center due to a homogeneously charged infinite thick slab (thickness linear with z, within the slab, and constant outside (12 N/C). The field is to the slab. ELECTRONICS AUTOMATION ENGINEERING a) Determine the charge density in the slab. MECHANICAL ENGINEERING PHYSICS II JUNE 2017 b) Determine the electric field at (0,0,a) after having hollowed out a sph FINAL radius a/2, centered at the coordinate origin.EXAM 1. The figure shows the plot of the electric field z-component, Ez , versus z (left) due to a homogeneously charged infinite thick slab (right), where thickness 2a = 10 cm. Ez is linear with z within the slab, and constant outside (12 N/C). The field is perpendicular to the slab. (a) Determine the charge density in the slab. (b) Determine the electric field at point (0, 0, a) after having hollowed out a spherical cavity of radius a/2 centered at the origin of coordinates. (c) Calculate the electric field at point (0, 0, a/2) if the charge density in the slab is given by the expression ρ(z) = Az 2 , where A = 2.5 × 10−6 C/m5 . 2. A hollow metal spherical shell of radius R1 = R is charged to a potential V . (a) Calculate the electric field everywhere. (b) Repeat part (a) if, maintaining the previous potential connected, the shell is surrounded by another concentric shell of radius R2 = 2R connected to the ground. (c) For the case of part (b), what would be the maximum potential V at which the inner shell could be connected before air breaks down if R = 10 cm? Assume that air has a breakdown field strength of 3 MV/m and dielectric constant of 1, and that the potential at infinity is zero, the same as ground. y 3. The figure shows the cross section of radius 2R of an infinitely long cylindrical cable. The cable carries two currents I going in opposite directions. One goes in the positive z direction and is uniformly distributed over a circle of radius R, and the other goes in the negative z direction I and 2R is uniformly distributed over the rest of the cross section. O Calculate the magnetic field B (a) at points x > 2R,Ry = 0 I and (b) at points 0 < x < 2R, y = 0. 4. Two infinite parallel straight wires carrying a current I in opposite directions, and a rectangular coil of sides a and b are in the same plane, as shown in the Figure. Find: (a) The magnetic field B as a function of y inside the coil. (b) The magnetic flux through the coil. (c) The induced e.m.f. in the coil when the current I varies in time as t ≤ 0, I = 0; 0 ≤ t ≤ T, I = αt; t ≥ T, I = αT. y I 2R x x O R I y y I c b I I a c c a b c I PHYSICAL CONSTANTS e = 1.6 × 10−19 C K = 9 × 109 N · m2 /C2 ε0 = 8.85 × 10−12 C2 /N · m2 µ0 = 4π × 10−7 N/A2 ELECTRICITY F = qE I ΦE = C= Q V Qenclosed ε0 1 1 U = QV u = εE 2 2 2 E · dA = MAGNETISM F = qv × B µ = N IA dF = Idl × B τ =µ×B µ0 Idl × ur dB = 4π r2 I B · dl = µ0 Ienc I B = µ0 (H + M) = µH H · dl = If Z dΦB ΦB = B · dA E =− dt E = −L dI dt 1 U = LI 2 2 u= 1 B2 2 µ