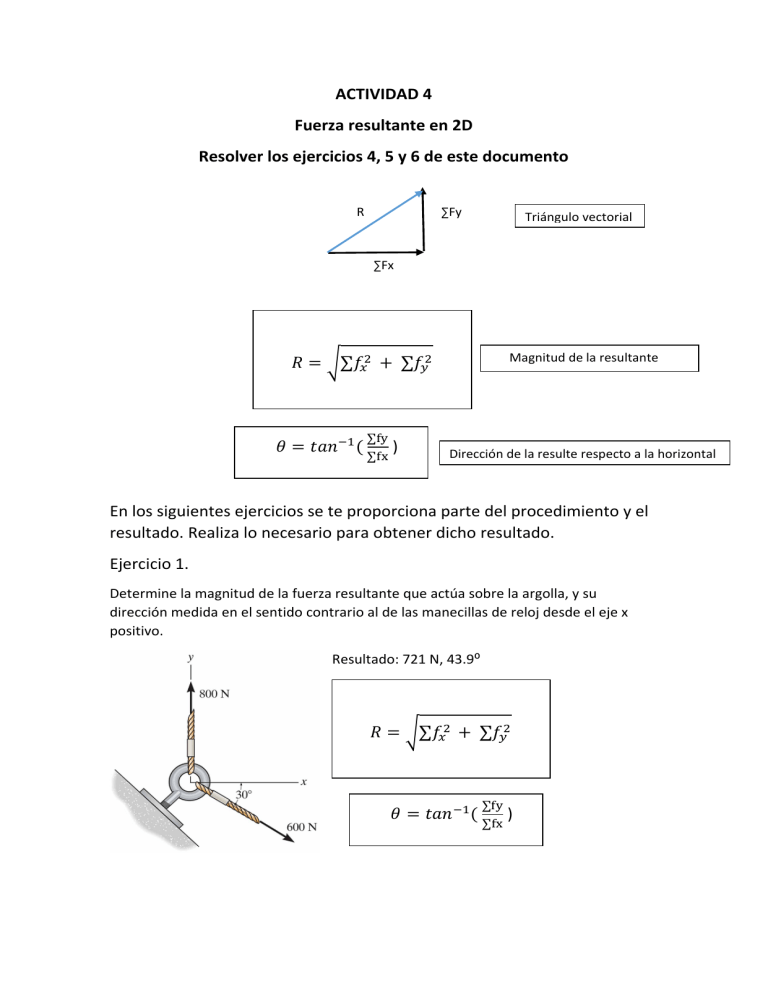
ACTIVIDAD 4 Fuerza resultante en 2D Resolver los ejercicios 4, 5 y 6 de este documento R ∑Fy Triángulo vectorial ∑Fx Magnitud de la resultante 𝑅𝑅 = �∑𝑓𝑓𝑥𝑥2 + ∑𝑓𝑓𝑦𝑦2 𝜃𝜃 = 𝑡𝑡𝑡𝑡𝑡𝑡−1 ( ∑fy ∑fx ) Dirección de la resulte respecto a la horizontal En los siguientes ejercicios se te proporciona parte del procedimiento y el resultado. Realiza lo necesario para obtener dicho resultado. Ejercicio 1. Determine la magnitud de la fuerza resultante que actúa sobre la argolla, y su dirección medida en el sentido contrario al de las manecillas de reloj desde el eje x positivo. Resultado: 721 N, 43.9⁰ 𝑅𝑅 = �∑𝑓𝑓𝑥𝑥2 + ∑𝑓𝑓𝑦𝑦2 𝜃𝜃 = 𝑡𝑡𝑡𝑡𝑡𝑡−1 ( ∑fy ∑fx ) Ejercicio 2. El extremo de la barra O mostrado en la figura está sometido a tres fuerzas coplanares (significa que las 3 fuerzas están en un mismo plano). Determine la magnitud y la dirección de la fuerza resultante. FR = 485 N θ= 37.8⁰ respecto al eje de las x negativo 𝑅𝑅 = �∑𝑓𝑓𝑥𝑥2 + ∑𝑓𝑓𝑦𝑦2 𝜃𝜃 = 𝑡𝑡𝑡𝑡𝑡𝑡−1 ( Ejercicio 3 ∑fy ∑fx ) La camioneta se va a remolcar con dos cuerdas. Determine las magnitudes de las fuerzas FA y FB que actúan en cada cuerda para desarrollar una fuerza resultante de 950 N dirigida a lo largo de eje x positivo. Considere θ = 50⁰ Triángulo vectorial FA R = 950 N De la ley de los senos: (950/sen 110⁰) = (FB/sen20⁰) FB = 346 N (950/sen 110⁰) = (FA/sen50⁰) FA = 774 N FB Ejercicio 4 Si θ = 30⁰ y T = 6 kN, determine la magnitud de la fuerza resultante que actúa sobre la armella roscada y su dirección medida en el sentido de las manecillas del reloj desde el eje x positivo. 8.67 kN, 63.05⁰ F.R= 8.67Kn Ф= 3.05° 𝐹𝐹𝐹𝐹 = √𝑇𝑇2 + (8𝐾𝐾𝐾𝐾2) − 2 cos 𝜃𝜃 𝐹𝐹𝐹𝐹 = √(6𝐾𝐾𝐾𝐾2) +(8𝐾𝐾𝐾𝐾2) −2cos𝜃𝜃 F.R= 8.67KN 𝜃𝜃 = 45 − 𝛽𝛽 = 0 Ejercicio 5 6𝐾𝐾𝐾𝐾 -------sin 𝛽𝛽 = 8.67/ 𝑠𝑠𝑠𝑠𝑠𝑠75° = 45 − 41.98 = 3.05° Si la fuerza F debe tener una componente a lo largo del eje u con magnitud Fu = 6kN, determine la magnitud de F y la magnitud de su componente Fv a lo largo del eje v. Observe que en este caso los ejes de referencia u y v no son perpendiculares, esto es, no se trata de un sistema rectangular. Esto implica que no sea posible utilizar la trigonometría del triángulo rectángulo, debiéndose recurrir a la ley de los senos o cosenos en la solución FR=ley de senos 6𝑘𝑘𝑛𝑛 𝐹𝐹 = 𝛿𝛿𝑒𝑒𝑛𝑛(30) 𝑠𝑠𝑒𝑒𝑛𝑛(105) 𝐹𝐹 = 6𝑘𝑘𝑘𝑘(𝑠𝑠𝑒𝑒𝑛𝑛30) 𝑆𝑆𝑒𝑒𝑛𝑛(105) 𝐹𝐹 = 3.10𝑘𝑘𝑘𝑘 Fv=ley de senos F = 3.11 kN Fv = 4.39 kN Ejercicio 6 6𝑘𝑘𝑛𝑛 𝐹𝐹𝑣𝑣 = 𝛿𝛿𝑒𝑒𝑛𝑛(45) 𝑠𝑠𝑒𝑒𝑛𝑛(105) 𝐹𝐹 = 6𝑘𝑘𝑘𝑘(𝑠𝑠𝑒𝑒𝑛𝑛45) 𝑆𝑆𝑒𝑒𝑛𝑛(105) 𝐹𝐹 = 4.39 Determine la magnitud y la dirección de la fuerza resultante. 𝐹𝐹1𝑥𝑥 = 0 𝐹𝐹1𝑦𝑦 = 300 𝐹𝐹2𝑥𝑥 = −450 𝑐𝑐𝑐𝑐𝑐𝑐 45 = −318.2 𝐹𝐹2𝑦𝑦 = 450 𝑠𝑠𝑠𝑠𝑠𝑠 45 = 318.2 𝐹𝐹3𝑥𝑥=35600=360 𝐹𝐹3𝑦𝑦=45600=480 𝑅𝑅=√Σ𝐹𝐹𝐹𝐹2+Σ𝐹𝐹𝐹𝐹2= 𝑅𝑅=√28,348.76+421,651.24= 671𝑁𝑁 tan−1(671)=89.91







