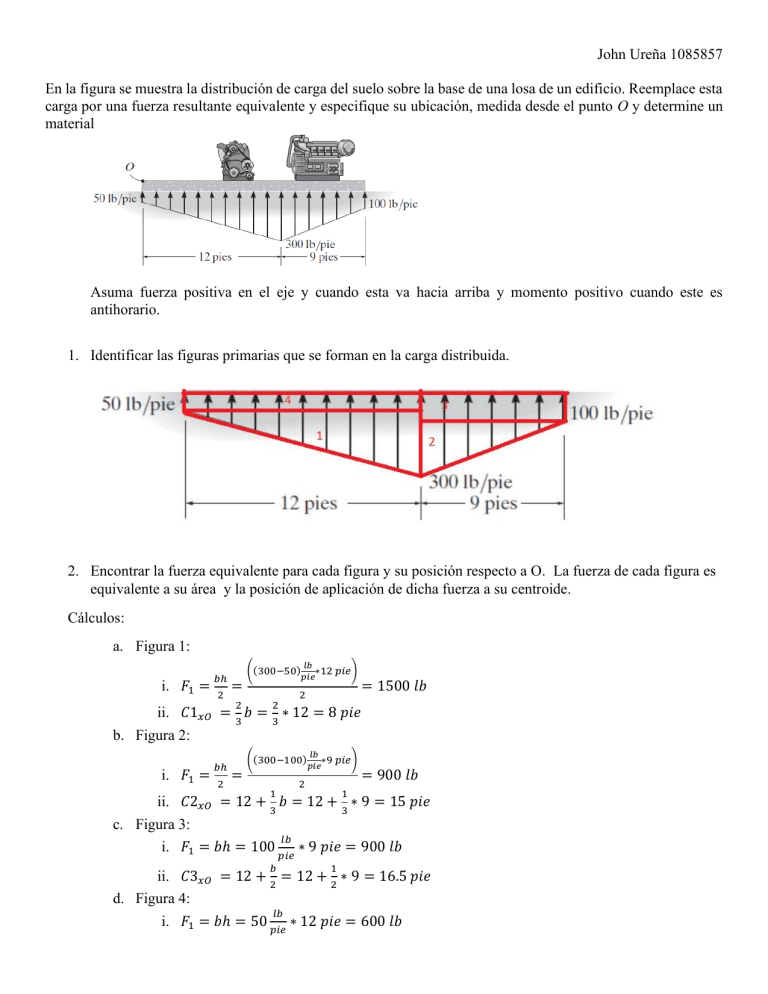
John Ureña 1085857 En la figura se muestra la distribución de carga del suelo sobre la base de una losa de un edificio. Reemplace esta carga por una fuerza resultante equivalente y especifique su ubicación, medida desde el punto O y determine un material Asuma fuerza positiva en el eje y cuando esta va hacia arriba y momento positivo cuando este es antihorario. 1. Identificar las figuras primarias que se forman en la carga distribuida. 2. Encontrar la fuerza equivalente para cada figura y su posición respecto a O. La fuerza de cada figura es equivalente a su área y la posición de aplicación de dicha fuerza a su centroide. Cálculos: a. Figura 1: i. 𝐹1 = 𝑏ℎ 2 ((300−50) = 2 𝑙𝑏 ∗12 𝑝𝑖𝑒) 𝑝𝑖𝑒 2 2 = 1500 𝑙𝑏 ii. 𝐶1𝑥𝑂 = 3 𝑏 = 3 ∗ 12 = 8 𝑝𝑖𝑒 b. Figura 2: i. 𝐹1 = 𝑏ℎ 2 ((300−100) = 𝑙𝑏 ∗9 𝑝𝑖𝑒) 𝑝𝑖𝑒 2 1 = 900 𝑙𝑏 1 ii. 𝐶2𝑥𝑂 = 12 + 3 𝑏 = 12 + 3 ∗ 9 = 15 𝑝𝑖𝑒 c. Figura 3: 𝑙𝑏 i. 𝐹1 = 𝑏ℎ = 100 𝑝𝑖𝑒 ∗ 9 𝑝𝑖𝑒 = 900 𝑙𝑏 𝑏 1 ii. 𝐶3𝑥𝑂 = 12 + 2 = 12 + 2 ∗ 9 = 16.5 𝑝𝑖𝑒 d. Figura 4: 𝑙𝑏 i. 𝐹1 = 𝑏ℎ = 50 𝑝𝑖𝑒 ∗ 12 𝑝𝑖𝑒 = 600 𝑙𝑏 𝑏 ii. 𝐶4𝑥𝑂 = 2 = Figura Fuerza (lb) 1 2 3 4 1500 900 900 600 12 2 = 6 𝑝𝑖𝑒 Posición respecto a O (pie) 8 15 16.5 6 3. Calcular el momento respecto a O para encontrar la fuerza equivalente resultante. Respecto al punto O todos los momentos son anti horarios Cálculos: a. Figura 1: i. 𝑀1 = 𝐹 ∗ 𝑟 = 8 ∗ 1500 = 12000 𝑙𝑏 ∗ 𝑝𝑖𝑒 b. Figura 2: i. 𝑀2 = 15 ∗ 900 = 13500 𝑙𝑏 ∗ 𝑝𝑖𝑒 c. Figura 3: i. 𝑀3 = 16.5 ∗ 900 = 14850 𝑙𝑏 ∗ 𝑝𝑖𝑒 d. Figura 4: i. 𝑀4 = 6 ∗ 600 = 3600 𝑙𝑏 ∗ 𝑝𝑖𝑒 Figura Fuerza (lb) 1 2 3 4 1500 900 900 600 posición respecto a O (pie) 8 15 16.5 6 Momento (Lb*pie) 12000 13500 14850 3600 4. Para encontrar la fuerza resultante, se realiza sumatoria de fuerzas en todos los ejes y luego, se aplican las fuerzas en las posiciones que generen un momento equivalente al calculado con antelación, el momento resultante total debe ser: 𝑀𝑟𝑒𝑠 = 12000 + 13500 + 14850 + 3600 = 43950 𝑙𝑏 ∗ 𝑝𝑖𝑒 𝐹𝑦𝑟𝑒𝑠 = 1500 + 900 + 900 + 600 = 3900 𝑙𝑏 Partiendo del conocimiento de que momento es Fuerza*brazo (r), si dividimos el momento resultante por la fuerza encontraremos el brazo de aplicación respecto a O. 𝑀 = 𝐹 ∗ 𝑟; 𝑟𝑂 = 𝑟= 𝑀 𝐹 43950 = 11.269 𝑝𝑖𝑒 3900 PARTE II – CALCULO DE MOMENTO MAXIMO PARA SELECCIÓN DEL MATERIAL Calculamos las fuerzas incógnitas de las cargas haciendo sumatoria de momento respecto a O y sumatoria de fuerza en Y. ∑𝐹𝑌 = 0; 600 + 1500 − 𝐹1 + 900 + 900 − 𝐹2 = 0 ∑𝑀𝑂 = 0; 12000 + 13500 − (𝐹1 ∗ 8) + 14850 + 3600 − (𝐹2 ∗ 16.5) = 0 Resolviendo el sistema de ecuaciones obtenemos 𝐹1 = −2400𝑙𝑏 ; 𝐹2 = −1500 𝑙𝑏 Separamos en 4 secciones de 0 a 8, 8 a 12, 12 a 16.5, 16.5 a 21 Dibujando el diagrama de momento y cortante Vemos que el cortante máximo es V= -1333.33lb y que el momento máximo es M = -3377.77 lb*pie Ahora, utilizando esta información, vamos a elegir un material. El factor de seguridad recomendado para nuestro tipo de carga, que es muerta para madera de construcción es 7. Escogemos madera porque tenemos un esfuerzo relativamente baja de solo 0.0638 Mxpa asumiendo un área unitaria ya que no se especifica. Entonces para un factor de seguridad N=7, necesitamos una madera que soporte 𝑆𝑢 = 7 ∗ 0.0638 = 0.4466 𝑀𝑝𝑎 Nuestra madera se encuentra en compresión perpendicular al grano. Considerando los efectos de la humedad, la madera GL24C BS11K, madera laminada encolada estructural, resiste exitosamente nuestra carga. La carga luego de aplicar el factor de seguridad es 0.47 Mpa, la resistencia del material es de 2.4 Mpa pero su resistencia a compresión baja hasta un 30% debido a los efectos de la humedad, como vivimos en el Trópico y el uso de la imagen parece de un taller y siempre se derrama aceites lubricantes y demás, se debe tomar en cuenta. A máxima humedad la resistencia baja a un 30% que seria 0.72 Mpa. 0.0638 < 0.47 < 0.72 𝑀𝑝𝑎 Bibliografía https://www.interempresas.net/Madera/Articulos/106945-Madera-laminada-encolada-(MLE).html https://www.elconstructorcivil.com/2011/02/propiedades-de-la-madera-variabilidad.html Vanegas, L. V. (2018). Diseño de elementos de máquinas (Primera Edición ed.). Universidad Tecnológica de Pereira Centro Recursos Informáticos y Educativos, CRIE.
